基于改进粒子群算法的含DG配电网无功优化

鲁裕婷, 赵天乐, 都洪基, 朱鑫要

(1. 南京理工大学自动化学院,江苏 南京 210094； 2. 国网江苏省电力有限公司电力科学研究院，江苏 南京 211103)

0 引言

分布式电源(distributed generation，DG)是一种新兴的供电电源，采用分布式发电具有投资小、灵活、高效、环保、能调节电网负荷峰谷差等优点[1-3]，但是越来越多的DG接入配电网，改变了原有系统的潮流分布，影响系统的电压、损耗以及可靠性等[4-6]。通过对系统进行无功优化，可以提高电网稳定性，有效地降低网损，因此研究DG的无功优化有重要意义[7]。

电力系统的无功优化问题在数学上是一个非线性和多约束的规划问题，可通过建立相应的无功优化数学模型进行求解。文献[8]建立了以降低地区电网网损、抑制电压波动为综合目标的地区电网模糊动态无功优化调度模型。文献[9]建立了含DG配电网络多目标无功优化模型。传统的粒子群算法(particle swarm optimization, PSO)结构简单，参数调节较少，但是局部收敛性较差。文献[10]改进了PSO，对算法中的粒子进行量化处理，通过蒙特卡罗仿真确定粒子的位置。该方法能有效改善算法收敛性差的问题，但计算时间较长。文献[11]在PSO算法的基础上加入了蚁群算法(ACO),首先用PSO进行寻优，将寻优到的结果作为ACO的初始解继续寻找最优解，这种混合PSO-ACO算法收敛性能较好，并且缩短搜索时间。文献[12]在PSO的基础上进行分群和裂变，保持粒子的多样性，避免收敛早熟，又通过合群和变异，加强算法的搜索精度，提高收敛稳定性。

文中在PSO的基础上进行改进，引入位置方差改善算法容易陷入局部最优解的问题。选用燃气轮机组作为容量固定的DG代表，风力发电机组作为间歇性DG的代表，在IEEE14节点系统这两种类型的DG，利用MATLAB对改进后的算法进行编程计算得到补偿地点的最佳补偿容量，以达到网损和电压质量的综合最优。

1 含DG的无功优化模型

1.1 目标函数

目标函数为网损和电压质量综合最优[13]，表示如下：

(1) 系统网损：

(1)

式中：Nk为系统支路的数量；Gk(i,j)为支路之间的电导；Vi，Vj，θi，θj分别为电压的幅值和相角。

通过调整电网无功的分布来降低电网有功网损是配电网无功优化的主要目标之一，保证电网的安全电压水平而不发生电压崩溃是配电网无功优化的另一个重要目标。

(2) 电压平均偏离[14]：

(2)

式中：λ为电压越界罚因子；Vi为节点i实际的电压；VNi为节点i的额定电压；N为系统节点数量。

最终的目标函数应使电网有功网损最小以及节点电压平均偏移最小[13]。引入权系数λ1，λ2，对目标函数进行归一化处理，得到最终的目标函数为：

(3)

1.2 约束条件

无功优化的约束条件包括等式约束和不等式约束，等式约束即为潮流约束，如式4。

(4)

式中：Pis，Qis分别为注入节点的有功功率和无功功率，注入功率包括负荷的(为负)功率，也包括补偿设备的注入无功和分布式电源的注入有功和无功；Pi，Qi分别为节点的计算功率；Gij，Bij分别为节点i和节点j之间的电导和电纳；δij为节点i、j之间的相位差。

不等式约束包括节点电压幅值约束、电容器的投切容量约束、燃气轮机组的有功无功输出约束、有载调压变压器的档位约束。其中，电容器的投切容量、燃气轮机组的功率输出和变压器的档位为控制变量，节点电压幅值为状态变量。燃气轮机组代表输出容量固定的DG，而有载变压器的节点被视为平衡节点，其电压也是保持不变的。所以控制变量只有电容器的投切容量，即为PSO中输出的控制变量。

节点电压约束：

Uimin≤Ui≤Uimax

(5)

电容器的补偿容量约束：

0≤Qci≤Qcmax

(6)

式中：Uimin和Uimax分别为节点i电压幅值的下限和上限；Qcmax为无功补偿的最大出力。

2 改进PSO

2.1 PSO

PSO将粒子运动的每一个位置当作问题的一个解，构建适应度函数对解的优劣进行评价，对于每个粒子Xi有一个位置变量Xi=(xi1,xi2,…,xin)，i∈[0,m]，m为种群中粒子的个数，n为解的维数。粒子在解空间中运动具有速度变量Vi=(vi1,vi2,…,vin)，在移动过程中粒子的历史最优解为Pi=(pi1,pi2,…pin)，全局最优解为Pg=(pg1,pg2,…pgn)，每个粒子根据历史最优解和全局最优解的位置更新速度变量和位置变量，粒子的速度和位置更新公式为[15-16]：

(7)

2.2 引入位置方差进行变异

PSO在求解过程中遇到很多问题，其中最严重的问题是经常陷入局部最优解[17-18]，为改善这个问题，对算法进行相应的改进。

(8)

定义粒子群的位置方差为：

(9)

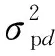
(10)

如果粒子群的位置方差很大，表明种群中的粒子很分散，这种情况下不容易陷入局部最优解。一般情况下，随着计算的进行，种群的位置方差越小，表明粒子逐渐向着一个解移动，这个解可能是全局最优解，也可能是一个局部最优解，因此有必要采取一定的变异算法，使粒子位置发生突变，避免整个种群陷入局部最优解。

设第k次迭代中粒子xi的适应度值为fi，所有粒子的适应度平均值为fav，全局最优粒子的适应度值为fmin。根据全局最优粒子适应度值与某粒子当前适应度的比值σ，将粒子划分为3类：第一类粒子的适应度较好；第二类粒子的适应度相对较好；第三类粒子的适应度较差。

(1) 对于适应度较好的粒子(σ2≤σ≤1)，取σ2=0.9，这类粒子可能位于全局最优解附近，也可能位于局部最优解附近，对速度进行变异：

vid=(2rand-1)Vdmax

(11)

(2) 对于适应度相对较好的粒子(σ1<σ<σ2)，取σ1=1.5×10-10，粒子向着种群的全局最优解移动，放宽粒子的适应度值，使粒子向更广阔的空间分布，避免种群陷入局部最优解，对粒子速度和位置都进行变异：

(12)

(3) 对于适应度很差的粒子(0<σ≤σ1)，对粒子的速度和位置进行变异：

(13)

2.3 改进PSO流程

应用改进的PSO进行含DG的配电网无功优化，其编程包括两个方面的内容：一是含DG的潮流计算编程，二是改进PSO编程，实现流程见图1。

图1 无功优化算法流程Fig.1 Flow chart of reactive power optimization algorithm

3 算例分析

计算的基本模型选取IEEE14节点配电网模型，这里将调换原来模型的第1个节点编号和第14个节点。在10节点接一台燃气轮机组，额定容量为2 MW，0.8 Mvar，其容量保持不变；风力发电机组接第1个节点，共有3台机组，每台机组的额定容量为700 kW。并联电容器的安装位置为节点5、6、9、11、13，如图2所示。

图2 IEEE14节点的配电网模型Fig.2 Distribution network model of IEEE14 node

以100 MV·A为基准容量，基准电压为网络的额定电压23 kV，节点14为潮流计算的平衡节点。目标函数部分，电压越限的罚因子取3，网损的权系数取0.8，网络电压平均偏差权系数取0.2。具体的无功优化结果如表1所示。

表1 各电容器最佳补偿容量Tab.1 Optimum compensation capacity of each capacitor

由于上级节点为变电站变压器的平衡节点，风力发电机组有功输出的变化只会影响该馈线相关的无功补偿装置(节点13)的输出，同时由于其在输出有功时需要吸收无功，所以有功输出的增加也会使得附近节点的无功补偿容量增加。

系统网损和电压偏离的结果如表2，其中第一行的数据为无无功补偿出力、DG输出为0时，系统的网损和平均电压偏离；第二行为有无功补偿出力、无DG出力的情况；后面7行则为有无功补偿出力且燃气轮机组出力恒定、风力发电机组不同的有功出力对系统目标函数的影响。

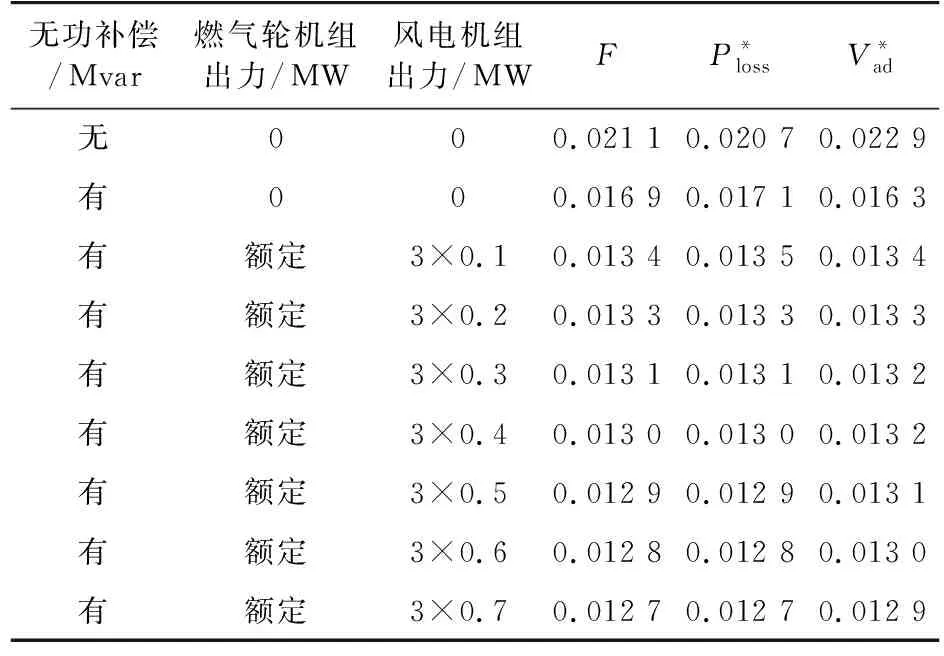
表2 目标函数计算结果Tab.2 Result of target function

由表2可见，无功补偿能有效降低系统的网损和提高电压质量，而DG的接入则进一步降低网损，提高系统电压水平，随着风力发电机组有功输出的增加，系统的网损也进一步减少。这是由于DG接入电网，减少了系统的有功流动和网损，燃气轮机组不仅能输出有功，也能输出无功，因此减少了系统无功功率的流动，提高系统的电压水平。另外，随着风力机组有功输出的增加，电压偏差也在减少，罚因子的引入使得优化结果中电压很难越限，最大程度上保证系统的电压质量和网损综合最优。

DG出力的增加对降低网损和提高电压质量的作用比较明显，但是这并不说明DG出力越大越好，因为过大的DG出力会导致大范围的反向潮流，甚至注入上级变压器节点，这在电力系统中是不允许的。随着风力发电机组出力的增加，吸收的无功功率增加，附近的无功补偿出力也会增加，最大程度减少系统无功功率的流动，达到减少网损的目的，但容易导致部分节点电压越限，如表3所示。

表3 增加1台风力发电机组目标函数计算结果Tab.3 Results of target function for adding a wind turbine

最后将文中改进算法与标准的PSO算法进行对比，2种算法分别计算了11次，收敛到最优解的次数和收敛到最优解的平均迭代次数如表4所示。

表4 改进算法与标准PSO结果对比Tab.4 Comparison between the improved algorithm and PSO

通过表4中的对比表明，改进算法较好地克服了标准PSO算法易陷入局部最优解的问题，具有较好的全局搜索能力。

4 结语

文中针对DG接入配电网的无功优化问题，采用计算位置方差的方法改进了PSO易陷入局部最优解的问题。通过对含DG的IEEE14 节点配电系统进行优化仿真。结果表明，无功补偿可以降低系统的网损，提高电压质量，DG的接入能进一步降低网损，提高系统的电压水平。对于容量较大的间歇性DG，比如风电，其有功输出的增加会使得接入该馈线相关的无功补偿装置的补偿量增加，计算结果也验证了所提的优化算法具有较好的优化性能和实用性能。