基于PSO-BP算法的高压输电线路故障分类

李达， 薛卿， 孔德健， 陈春强， 王金玉

(1.国网冀北电力有限公司检修分公司，北京 102488；2.东北石油大学 电气信息工程学院，黑龙江 大庆 163318)

0 引 言

电能在居民生活和工业生产中具有十分重要的地位，由于中国的能源分布特性导致需要电能长距离传输[1]。因此，高压输电线路的发展对于电能传输的可靠性和安全性有很大的影响。目前工业生产和居民生活对于电能的依赖越来越强。如果高压输电线路发生故障导致停电，并且无法短时间内快速消除故障，会给居民生活和工业生产造成很大的影响[2]。当线路发生故障时，首先要确定线路的故障类型，再对线路故障点进行快速定位，这能够有效减少寻找故障点所需的时间。对提高线路故障分类准确性有重要意义。

1 粒子群BP神经网络算法

1.1 PSO算法的基本原理

1.1.1PSO算法的数学描述

PSO算法主要是对函数进行优化调整，可以有效解决工程问题中的目标优化问题。PSO算法用数学方法可以解释为：在一个N维搜索空间中有一个群体，其由m个粒子组成，第i个粒子在粒子群的位置是xi=(xi1,xi2,…,xiN)T,i=1,2,…,m。将xi代入目标函数中就能求出适应度值，并根据适应度值的大小对xi是否为最佳位置作出判断[3]。在此粒子群中第i个粒子的速度为vi=(vi1,vi2,…,viN)T，粒子群中的粒子通过对最优个体极值pbest和最优全局极值gbest进行追踪来对自己进行更新，其更新公式为：

(1)

(2)

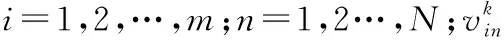
1.1.2PSO算法的改进

(3)

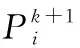
1.2 BP神经网络

神经网络是通过学习训练对各层的权值进行调整的过程，对输入的信息进行正向传播和反向传播以达到输出结果误差小和训练步数少的目的，其结构如图1所示。

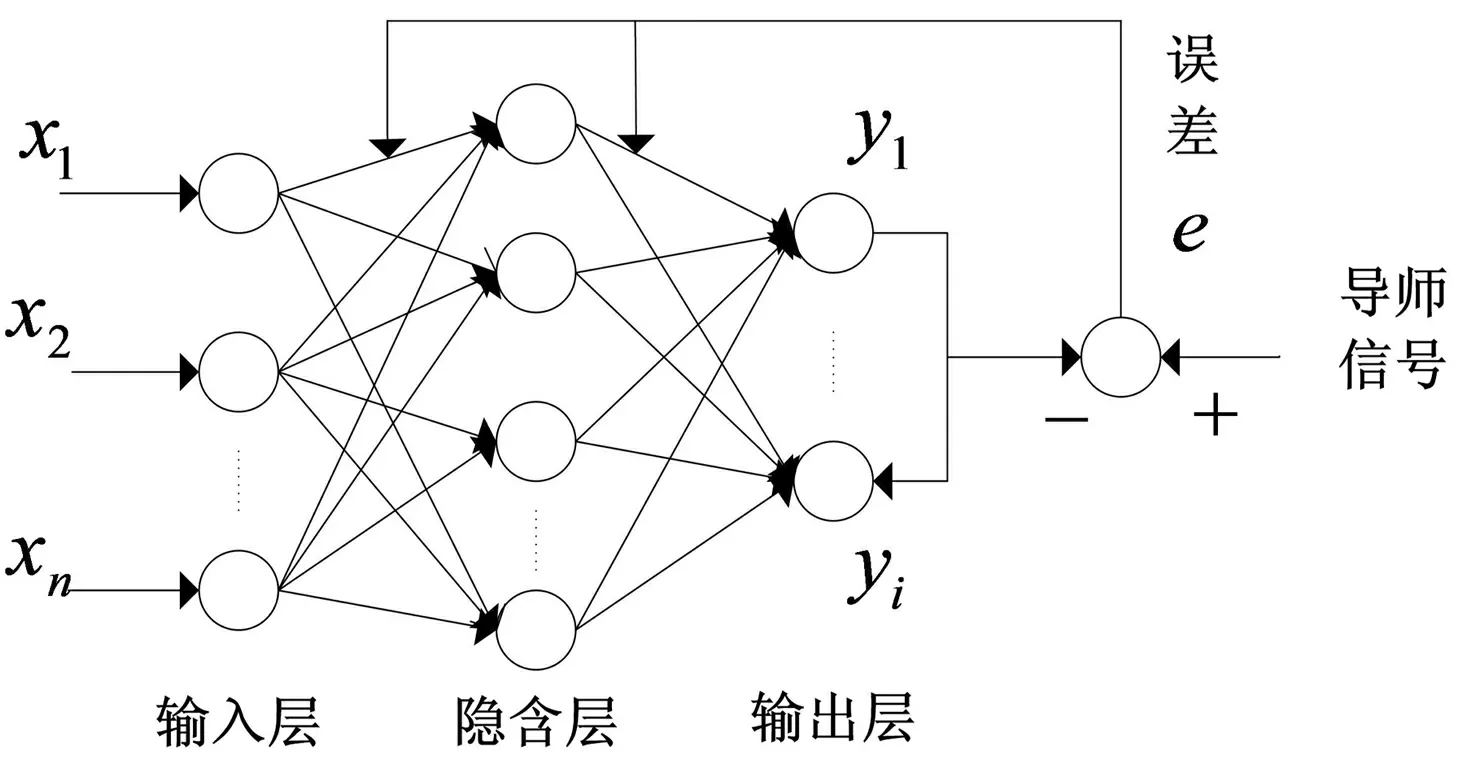
图1 神经网络学习结构图

对BP神经网络进行分析，并且选择Sigmoid型(简称S型)函数作为激活函数[5]。

以x为变量，其S型函数的表达式如下：

(4)

当输入第k个样本时，隐含层第j单元状态：

(5)

式中：wji为输入层到隐含层的网络权值；oki为输入第k个样本时，第i个单元节点的输出；θj为隐含层第j个单元的阈值。

输出层第m单元状态：

(6)

式中：wmj为隐含层到输出层的网络权值；okj为输入第k个样本时，第j个单元节点的输出；γm为输出层第m个单元的阈值。

隐含层第j个单元输出：

(7)

输出层第m个单元输出：

(8)

输出层第m个单元误差为：

δkm=(tkj-okj)×okj(1-okj)

(9)

式中：tkj代表网络的期望输出。

隐含层第j个单元误差：

(10)

隐含层第m单元到输出层第j单元权值调节为：

Δwmj(k+1)=ηδkmokj

(11)

式中：η为是神经网络学习率，通常该值得设定范围为0.01～0.8。

输入层到隐含层权值调节为：

Δwji(k+1)=ηδkjoki

(12)

输出层阈值调节为：

Δγm(k+1)=ηδkm

(13)

隐含层阈值调节为：

Δθj(k+1)=ηδkj

(14)

通过上述分析能够得出，学习率η的变化会影响网络权值，学习率η越大，网络权值变化也就越大，可以得出它对BP神经网络的学习过程有很大影响。

2 提取故障特征量

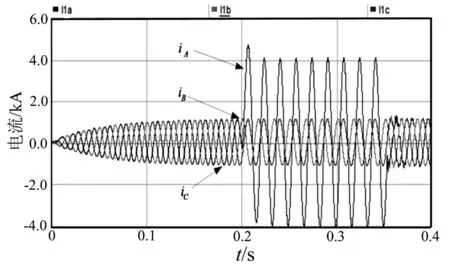
图2 A相接地故障电流波形

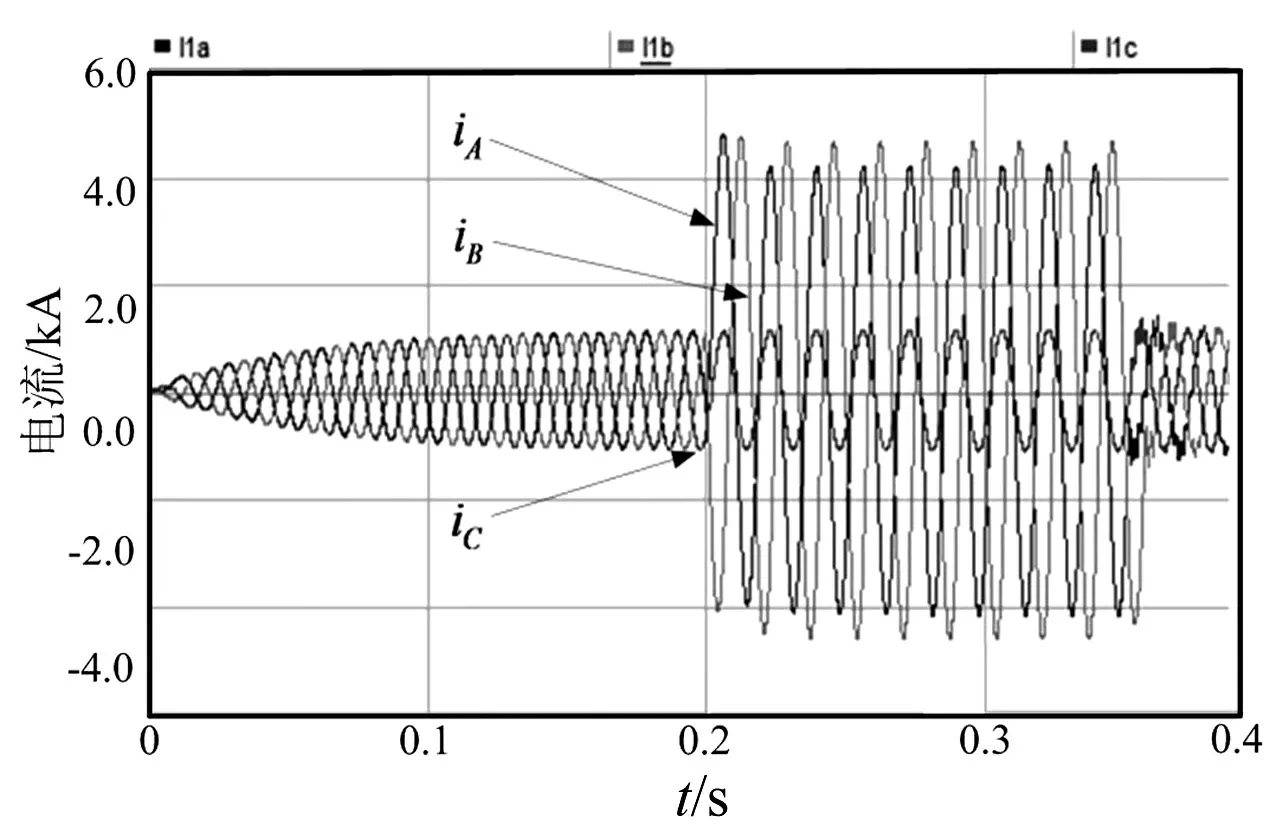
图3 AB两相接地短路故障电流波形

通过PSCAD软件对于线路单相接地故障和两相接地短路故障的电流波形如图2、图3所示。

故障特征量提取时的采样频率选择50 kHz，并且选择故障后5 ms的三相电流iA、iB、iC及零序电流i0为故障分析对象，利用小波变换局部化特性好的优点可以将提取到的信号的时频特性显示出来。采用db4小波对三相电流和零序电流进行8层分解，对三相电流和零序电流进行分解后可以得到高频细节信号系数d1(k)～d8(k)和低频近似信号系数d9(k)[6]。

三相电流的小波能量能够形成故障特征量T1。通过式(15)可以求解出三相电流的高频能量EA、EB、EC和归一化值eA、eB、eC，将初始设定的阈值和eδ比较，如果eδ大于设定的阈值则认为是1，如果小于设定的阈值则认为是0。从而形成故障特征量T1=[eA,eB,eC]。

(15)

零序电流小波能量可以形成故障特征量T2，将i0的低频能量E0进行三相电流高频能量的处理方法处理，也就是把阈值看作是1或0，从而形成特征量T2=[E0]。

(16)

式中：d09(k)为i0小波分解后低频近似信号系数。

故障特征量T3～T10是三相电流小波系数标准差。把iA、iB、iC各高频小波系数标准差σ(dAj)、σ(dBj)和σ(dCj)，j=1，2，…，8求取出来，并通过式(17)把高频小波系数标准差归一化，然后判断归一化后的σδ值，同样将σδ和设定的阈值进行比较，如果大于阈值就量化为1，如果小于阈值则量化为0，可以得出故障特征量[σA(j),σB(j),σC(j)]。

(17)

式中：max[σ(dj)]和min[σ(dj)]分别为σ(dAj)、σ(dBj)和σ(dCj)中的最大值和最小值。

把经小波变换得到的10种故障特征向量进行综合后就能够得出T=[T1,T2,…T10]T，也就是输电线路故障分类的特征向量，可以把特征向量作为故障分类的数据依据。

3 仿真验证

利用PSCAD建立一个输电线路长300 km的500 kV双端供电系统模型[7]，其中线路的主要参数设置为：x1=0.248 Ω/km，b1=0.39×10-5S/km，r1=0.021 Ω/km，x0=1.08 Ω/km，b0=0.261×10-5S/km，r0=0.249 Ω/km。此输电模型能够采集到不同位置、不同相角和不同故障类型的电压电流数据，从而能够得到故障样本数据共1 865组，用PSO-BP算法对输电线路故障类型分类，其理想条件下的分类结果如表1所示。

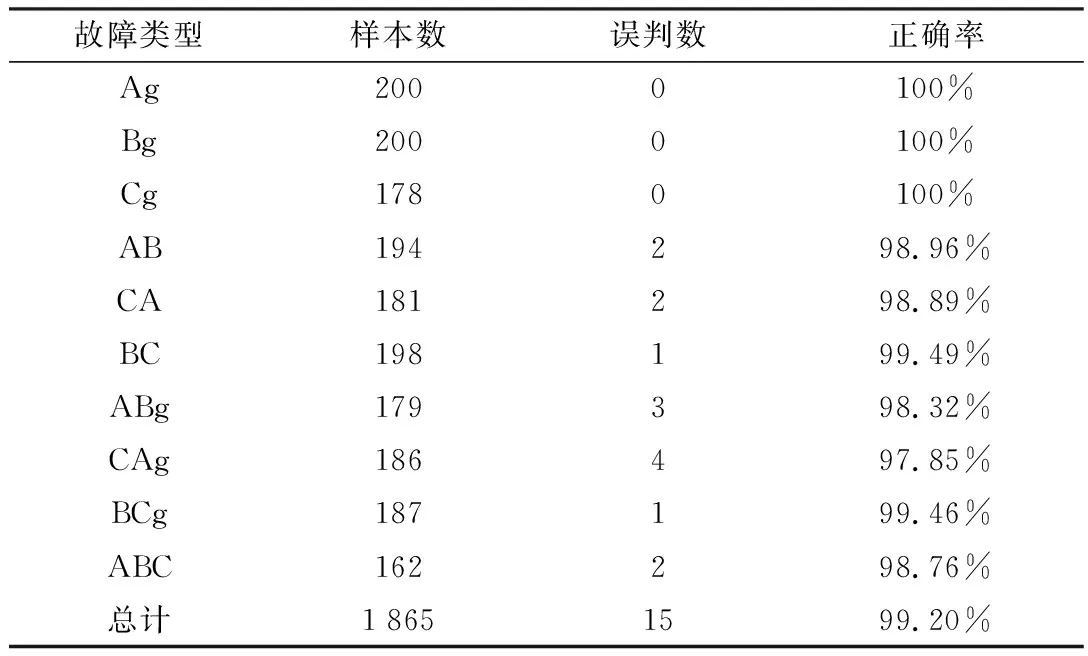
表1 理想条件下故障类型分类结果

这是在理想条件下的分类结果，线路实际运行中会受到很多因素的影响，下面对谐波对故障分类准确率进行分析，表2是在不同谐波下的分类结果。

通过表1和表2的对比能够看出，PSO-BP算法在有谐波影响时故障分类的准确率会降低，并且在谐波总失真增加时，准确率也会降低。但即便总谐波失真达到10%，故障分类的准确率仍能达到97.16%，可以较好地满足现场实际要求。

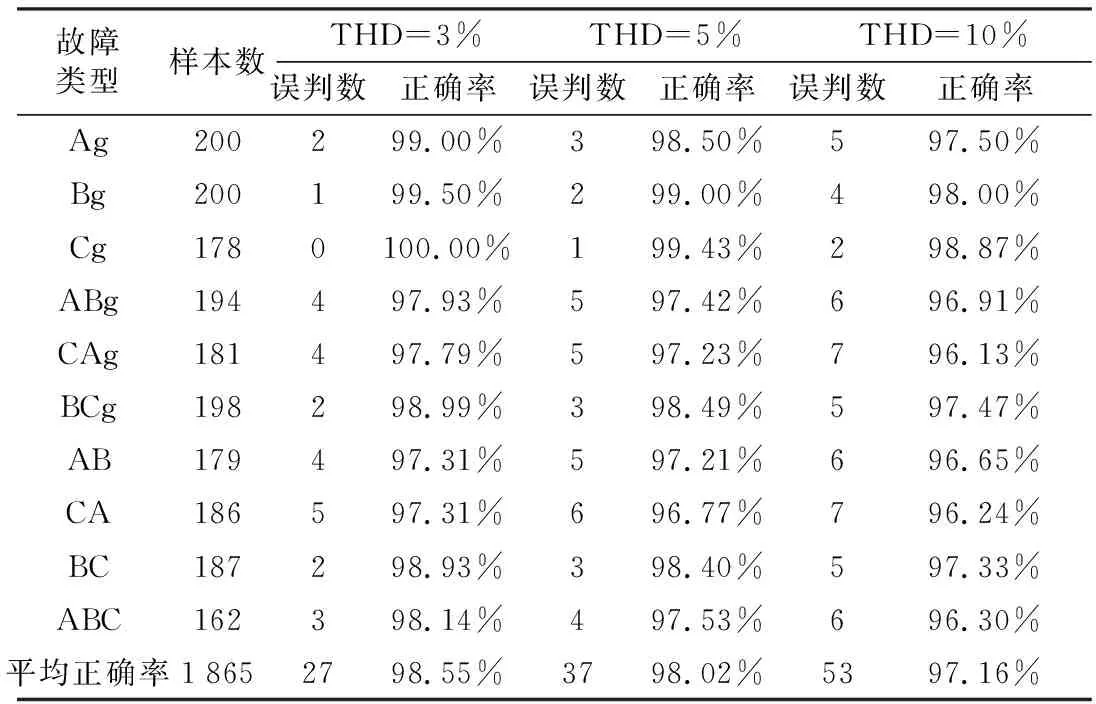
表2 三种谐波情况下的故障分类结果

4 结束语

针对传统BP神经网络算法进行高压输电线路故障分类不准确的弊端，提出利用PSO-BP算法提高输电线路故障分类的准确度。通过仿真验证结果可以得出，PSO-BP算法在高压输电线路故障分类方面具有十分理想的准确率，并且即便有谐波影响时仍然能够保证较高的准确率，可以满足高压输电线路现场实际要求。