利用Excel建立统计预测模型

◇刘惠娟

随着科学技术的进步和时代的快速发展，各级统计工作已经从以往的事后统计逐渐向对未来的预警预示转变，而基层的统计分析水平还停留在简单的同比、环比等初级水平。随着计算机技术的发展，大数据时代的来临，大量的统计计算均可由软件来实现。可进行统计分析的软件有许多，如SPSS，SAS，BMDP，MATLAB，BMDP 等。这些软件的优点是界面友好，统计功能强大，处理功能完善，可以进行二次开发，可直接用鼠标完成数据分析，图表描述等，能够提供常见的统计分析功能等。但是它们都存在着一些缺点：首先，软件价格较为昂贵，普及性低；其次这些软件命令和函数较为繁琐，入门不易；第三，软件系统配置要求高，不适合安装运行在公共使用的计算机上。

Office一直是较为流行的、功能强大的办公应用软件之一，它是迄今为止Microsoft公司推出的最为复杂的产品之一。Excel价格便宜，普及率高。利用它可以非常方便地制作出集文字、数字、图表、图形于一体的电子表格，并且可以使用公式和函数对表格中的数据进行复杂的运算，同时，它还可以通过便捷的操作来完成非常复杂的数据分析、统计及管理工作。本文即利用Excel 2007软件对长治地区1997～2016年农业统计数据进行分析，并成功设置柯布-道格拉斯（C-D）生产模型为例，为更好地利用这种办公软件，提高统计的预测预警功能，提供一种新思路。

一、案例选择

（一）统计数据的采用

长治位于山西省东南部、太行山南段，东部与河北邯郸、河南安阳为邻，西部与临汾相依，南部与晋城交界，北部与晋中腹地接壤。全境地势由西北向东南缓缓倾斜，东西长约150公里，南北宽约140公里，总面积13896平方公里。地理坐标为东经 111°55′～112°44′，北纬 35°11′～37°08′，平均海拔高度为1000米。长治属典型暖温带半湿润大陆性季风气候，雨热同季。年平均温度8.6℃～10.5℃，年平均降水537.4～656.7毫米，年平均湿度61%，年日照时数2418～2616小时，年平均无霜期在151.8～181.9天，年平均风速为1.1～2.3米/秒。是全省主要产粮区之一，非常适宜玉米作物的种植。

本文假定玉米产量是与农业生产资料（如播种面积和劳动力）和农业投入（如化肥施用量和农用机械量）等因素的有关的函数。《长治市统计年鉴》（1997-2016）提供了长治地区各县1997～2016年玉米年产量（Y）、玉米播种面积（X1）、农业劳动力（X2）、化肥施用量（X3）、农业机械量（X4）方面的数据，如表1。

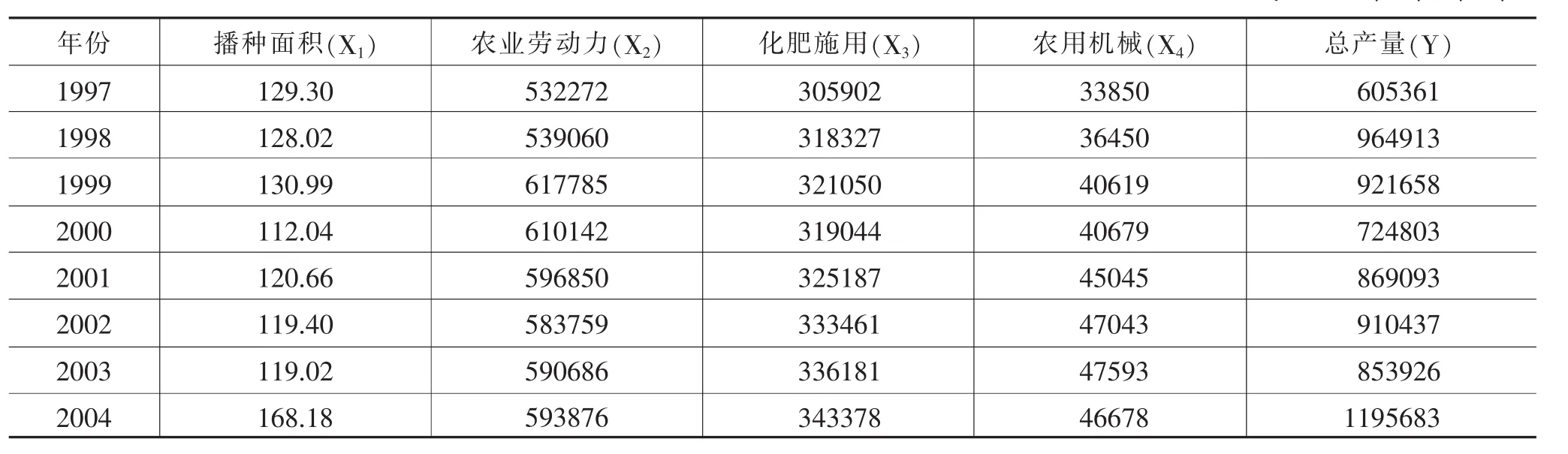
表1 长治1997～2016年农用机械及玉米产量的数据单位：千公顷、人、吨、台、吨

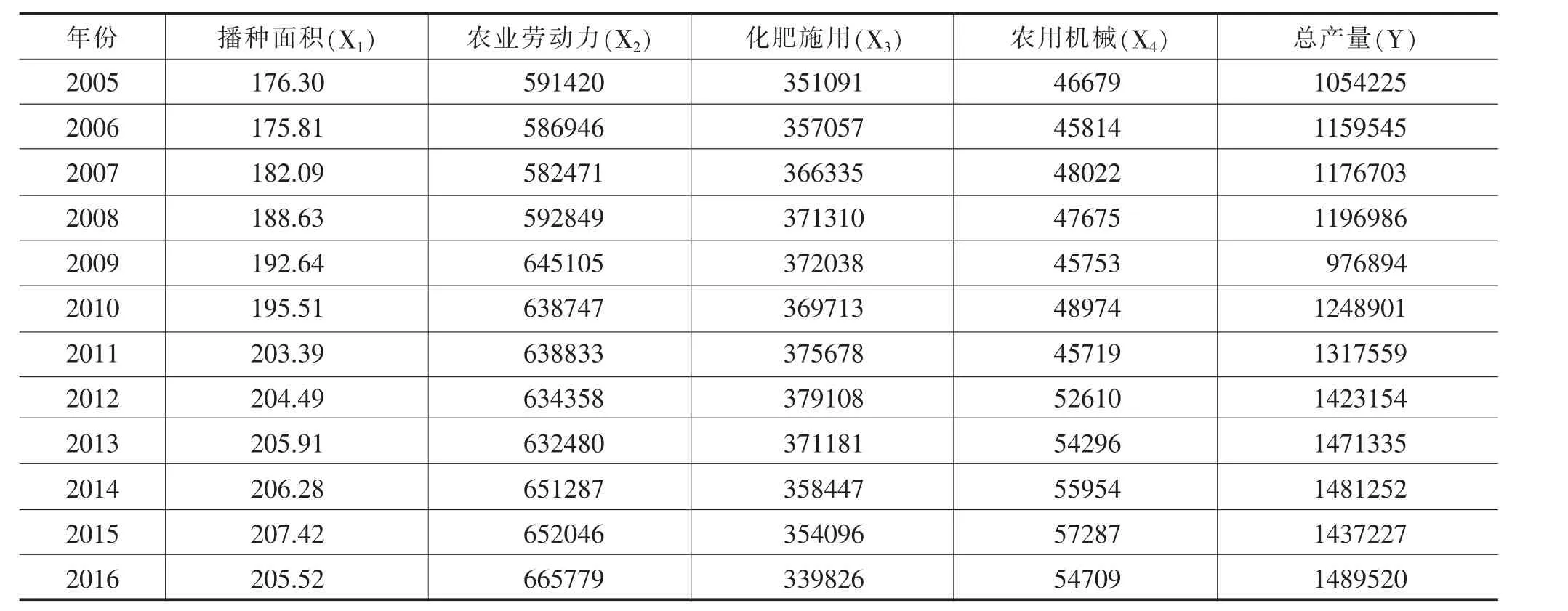
续表单位：千公顷、人、吨、台、吨

（二）统计预测及模型建立方法

柯布-道格拉斯生产函数是由美国经济学家保罗.道格拉斯（P.H.Douglas）和数学家查理.柯布（C.W.Cobb）根据历史统计资料研究20世纪初美国的资本投入和劳动投入对产量的影响时，得出的一种生产函数，是分析资源“投入”与产品“产出”之间经济数量关系最为常用的一种生产函数。农业生产过程是各种生产资源不断投入的过程，为了求得更高的收益，必须分析投入是否合理，总结经验，以便决定下一步生产再投入的增减。C-D生产函数以其使用方便，便于比较被广泛应用于农业技术经济中。利用C-D生产函数，可以估测各项投入要素和粮食转换率对农业产出的影响程度，从而判定那些是影响粮食产出的主要因素，那些是次要因素。本文假定玉米总产量（Y）为产出，玉米播种面积（X1）和农业劳动力（X2）为生存资料；化肥施用量（X3）和农用机械量（X4）为投入，那么假定的CD函数模型为：

其中，A表示影响生产的转化效率系数，i表示变量的序号，α表示几个变量对产量影响的弹性系数。

二、建模的方法与步骤

（一）“分析工具库”的加载

通常情况下，Excel并没有安装“分析工具库”，因此，需要先激活Excel的“数据分析”功能。步骤如下：打开Excel2007工作表，点击左上角“Office按钮”选择“Excel选项”，在弹出的对话框中点击“加载项”，选中“分析工具库”，点击“转到”，随机弹出“加载宏”界面，点击“确定”；查看“数据”菜单，可发现最后一栏新增“数据分析”命令。

（二）利用Excel进行回归分析

本文借用宫锡鸿、宫兆芳等采用Excel建立C-D函数数学模型的方法，先将各变量转换为对数进行回归分析，然后对得出的回归方程进行反对数转换，得出相应的C-D函数模型。具体步骤如下：

首先，将原始数据输入Excel表格中：打开Excel2007工作表，根据表1在工作表的A1：F1单元格区域依次输入“年份”“ 播种面积 X1”“农 业劳动力 X2”“化 肥施用量 X3”“农 用 机械量X4”“总产量Y”作为变量名称；在单元格A2：A21中依次键入年份1997～2016年，单元格B2：B21中依次键入表格第二列数据，单元格C2：C21中依次键入表格第三列数据，单元格D2：D21中依次键入表格第四列数据，单元格E2：E21中依次键入表格第五列数据，单元格F2：F21中依次键入表格第六列数据。

其次，将输入数据转换为对数：在单元格G1：K1中依次键入 X'1、X'2、X'3、X'4、Y'，在单元格 G2 中键入“=log10（B2）”，回车得到1997年农业耕种机械数值的对数值，用鼠标选中G2单元格，再用左键填充柄拖动至单元格G21。同样，在单元格H2 中键入“=log10（C2）”，并填充至单元格 H21，在单元格 I2、J2、K2 中键入“log10（D2）”、“log10（E2）”、“log10（F2）”，并填充至单元格I21、J21、K21。或选中G2直接用鼠标左键填充柄横向拖动至 K2，再纵向依次拖动至 G21、H21、I21、J21、K21，得到所有变量的对数值。

然后，进行多元回归分析：在菜单栏中选取“数据”→“数据分析”→“回归”，从而出现回归对话框。在回归对话框中，单击“Y值输入区域（Y）”在输入框右边的折叠按钮，然后在工作表中选取logY值区域＄K＄2:＄K＄21，用同样方法完成“X值输入区域（X）”的选择＄G＄2：＄J＄21，在“输出选项”框中选择“输出区域”单选框，并在其右面的框中键入“＄A＄24”，在“残差”框中选择“残差（R）”复选框。最后单击“回归”对话框中的“确定”按钮。这时，会在A24：A44行出现回归分析结果，在A48：A70行出现回测结果的对数值。多元回归分析结果为：F=25.06032871，常数项为3.316733799，四个回归系数分别为0.684353534、-0.300109061、-0.275458343、0.956677266。

据常数项、四个回归系数可以得到一个多元回归方程：

Y'=0.684353534X'1-0.300109061X'2-0.275458343X'3+0.956677266X'4+3.316733799

其中：Y'=logY、X'1=logX1、X'2=logX2、X'3=logX3、X'4=logX4。由回归分析表中可知，F临界值为1.71814E-06，此回归方程通过了α=0.05的F检验，显著性达到99.99%以上。

（三）将回归方程转换为C-D函数模型

将上述回归方程的常数项3.316733799进行反对数转换的方法是：在上述工作表中的空白处单击某一单元格，例如D73，以存放转换后的常数项；在菜单栏中点击“公式”，单击“Fx”，在弹出的对话框中的“搜索函数”框中键入“POWER”，点击“转到”，即在“选择函数”列表中出现“POWER”；选中“POWER”，单击[确定]，紧接着弹出的“POWER”对话框，在“Number”输入框中键入数码“10”，在“Power”输入框中输入常数项“3.316733799”，单击“确定”后，即在单元格D73中出现了常数项“3.316733799”的反对数“2073.642086”，因此，多元线性回归方程转化为柯布-道格拉斯生产函数：

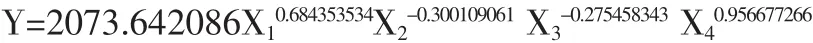
其中，转化效率系数为2073.642086，四个弹性系数分别为 0.684353534、-0.300109061、-0.275458343、0.956677266。

（四）模型的精度

模型的精度可以通过均值指标、稳定性指标和综合指标来确定。本文采用简单的均值测定法。步骤如下：对B51：B70的预测Y值进行反对数转换，即可得到玉米总产量的回测值。在单元格D50键入“回测值”，选取单元格D51，单击“公式”栏中“Fx”按钮，在弹出的函数对话框中“选择函数”列表中的选中“POWER”函数；点击“确定”，紧接着的弹出的“POWER”对话框，在“Number”输入框中键入数码“10”，在“POWER”输入框中键入“B51”，单击“确定”按钮后即可在单元格D51中出现年序1，即1997年的玉米产量回测值。选中单元格D51并用鼠标左键填充柄拖动至D70，即得各年序的产量回测值，将回测值与实际值进行比较。如表2，E50：E70中输入Y的实际值，F50:F70中计算出二者的误差。

在误差列表格下方，即Excel工作表的F71单元格中，单击“Fx”，在“选择函数”框中选取“AVERAGE”函数，点击“确定”，点击“Number1”右侧按钮，选中“F51：F70”，点击“确定”，即弹出数据“-3622”。表明该模型得出的Y值与实测值间的平均误差为“-3622”。

表2 C-D函数数学模型的回测值和实际值间的比较单位：吨

三、结论与讨论

（一）所建立的C-D模型结果分析

通过对1997～2016年玉米产量与各因素间的统计分析得到的C-D生产函数，通过了显著水平等于0.05的P检验和F检验，说明该模型可信度较高。修正样本可决系数R2=0.835128573，该模型的解释能力为83.5%。也就是说该模型在83.5%的程度上拟合了样本数据。通过均值测定法测定模型精度,显示该模型得出的Y值与实测值间的平均误差为“-3622”。分析结果显示：播种面积（X1）、农业劳动力（X2）、施肥总量（X3）和农用机械量（X4）的弹性系数分别为 0.684353534、-0.300109061、-0.275458343、0.956677266。可见，播种面积和农业机械的投入对玉米增产起到不可替代的作用。而近年来，农用耕地面积增长已临近极限，农业人口的保持也面临挑战，农业用肥也逐渐趋于科学合理，各因素对玉米产量的影响，都是通过进入土壤中的水分起作用，而这就对农用机械提出更高的要求。因此，下一步的工作应从机理上进一步研究提高亩产和生产劳动率着手。综上所述，此模型较为适用。

（二）Excel在统计分析中的应用

上述案例中，不对变量进行对数转换，而是直接进行回归分析，便可得出F=31.51257053，通过α=0.05的F检验的多元回归方程：Y=5282.591751X1-0.570067034X2-1.816859017 X3+21.03342716 X4+223433.9603。由以上建立的C-D函数模型和回归分析等步骤可以看出，Excel在进行数据输入、对数转换、多元回归分析、反对数转换等方面，均为简便快捷，因此建立模型也同样简便快捷。如果年代较长、变量较多，可更显示出Excel的强大的数学分析和建模功能。Microsoft Excel是最常用的办公软件，事实上，Excel在方差分析、主成分分析等各种分析方法，在灰色模型、空间面板、缺失面板等各种数学模型建立，在投资管理决策、动态监控决策等各个领域均可巧妙应用。如果能够充分利用与发挥，一定能为基层统计工作人员分析及预警预测发挥巨大的作用。