多次返回碰撞轨道对原子高阶阈上电离的贡献

王继玲,李婵,郝小雷,李卫东

(山西大学 理论物理研究所,山西 太原 030006)

0 引言

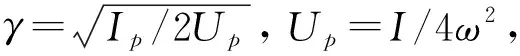
基于以上的半经典理论,在强场物理中,经典电子轨道的一些特征对于理解各种过程是至关重要的。这些显著的特征包括最大返回碰撞能量(3.17Up),以及电子能谱高能平台结构的截止位置在10Up[7]等等。在绝热隧穿中,上述这些特征能量的得出都是基于假设电子的初动量为零,忽略离子核对电子的库仑吸引作用,并且只考虑单次返回碰撞轨道贡献的情况下得出的结论,很少有人研究考虑库仑吸引作用后多次返回碰撞轨道对高能平台结构的影响。

本文利用半经典再散射模型(γ≪1),研究了氢原子在800 nm,1.3×1014W/cm2强激光场下多次返回碰撞轨道对高阶阈上电离的贡献。在研究过程中,我们考虑了电子隧穿后离子库仑势对电子的作用。

1 半经典再散射模型

半经典理论中,在激光场和库仑势的联合作用下,电子在任意时刻都有可能发生隧穿电离,并随后遵从经典力学规律沿特定轨道运动。电子轨道权重由电子的电离概率来决定,由Ammosov-Delone-Krainov(ADK)隧穿理论给出[11]。运动演化方程可由牛顿方程联立得出。

本文采用线偏振光,偏振方向为z方向,则激光场的形式为E(t)=(0,0,Ez(t)),其中Ez(t)=f(t)E0zcosωt。激光脉冲的包络形式为

(1)

其中E0z是激光振幅,ω是激光频率,T表示激光周期,(1)式表示电场的前五个周期振幅是恒定的,后三个周期以cos2的形式来模拟激光场的关闭。在强场物理中,一般采用原子单位,即m=e=ћ=1(文章后续的计算都采用原子单位)。

电子的隧穿电离可由量子隧穿理论求出,在激光场中,其隧穿过程的一维薛定谔方程(抛物坐标系下)为

(2)

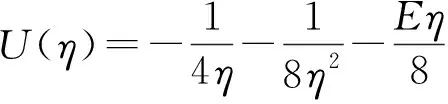
每一个轨道的权重(即隧穿的电离率),可通过ADK理论计算得到:

(3)

其中,

(4)

(5)

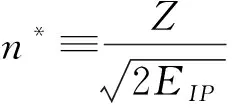
电子电离后的运动演化遵循经典力学规律,

(6)

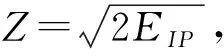
我们全程考虑库仑势与电子的相互作用,通过数值求解的方法,研究了多次碰撞轨道对高能平台的贡献[12]。

2 数值结果与分析

氢原子在波长800 nm,光强为1.3×1014W/cm2的线偏振激光场中的光电子能谱如图1所示。横坐标是光电子能量,单位是Up,纵坐标是对应的电离率。该能谱图包含了所有返回碰撞轨道的贡献。从图中可以看出:(1)在0-2 Up的低能区间,电子的产率随能量增大而快速下降;(2)在2-10 Up的高能区间,电子的产率较低但比较平坦,即高能平台结构。

0-2 Up的能谱主要是由被激光场加速但没有与母离子发生散射的直接电离电子导致的。对于直接电离电子,其在电场峰值处电离概率最大,但动能最小,而在电场为0处电子的电离概率最小,但动能最大(2 Up),所以整个分布呈现0-2 Up快速下降。在2-10 Up的高能区域出现了一个平台结构,主要起源于电子与母离子发生的背向散射。电子背向散射后被激光场再次加速后最终获得的最高能量10 Up,正是平台的截止位置。整个能谱与实验结果是相符合的[13]。

Fig.1 Photoelectron spectrum of Hydrogen atom in linearly polarized laser field. Ι=1.3×1014 W/cm2 and λ=800 nm图1 氢原子在波长为800 nm,光强为1.3×1014 W/cm2的线偏振激光场中的光电子能谱

下面我们对氢原子高阶阈上电离(平台结构)进行进一步的研究,得到了高阶阈上电离碰撞时刻分布如图2所示,横坐标是碰撞时刻,以周期为单位,纵坐标是相对应的电离率。从图2我们看到,0-1T区间有一个峰,之后每隔半个周期会出现一个峰。每个峰对应于某一次的电子返回轨道,我们称第n个峰对应的电子轨道为n次返回轨道。我们很直观地看到第一次返回轨道的贡献与第二次相比要小很多,从第三次返回开始贡献逐渐减小,所以多次返回轨道在研究中也应该被考虑进来。

Fig.2 Distribution of collision time of Hydrogen atom图2 氢原子的电子碰撞时刻分布图

图3为氢原子的不同返回碰撞轨道的光电子能谱。从图中很明显看出不同轨道的截止能量是不同的。第一次返回的截止能量最大为10.6 Up,第二次返回轨道的截止能量最小为6.8 Up,第三次截止能量为10 Up,第四次为7.1 Up。而且不同次返回轨道对平台不同部分的贡献不同。在2-6.8 Up区间第二次返回轨道贡献最大,在6.8-10 Up区间第三次返回轨道贡献最大,大于10 Up则只有第一次返回轨道有贡献。

Fig.3 Energy distribution corresponding to different return orbits图3 不同返回次数轨道对应的能量分布图

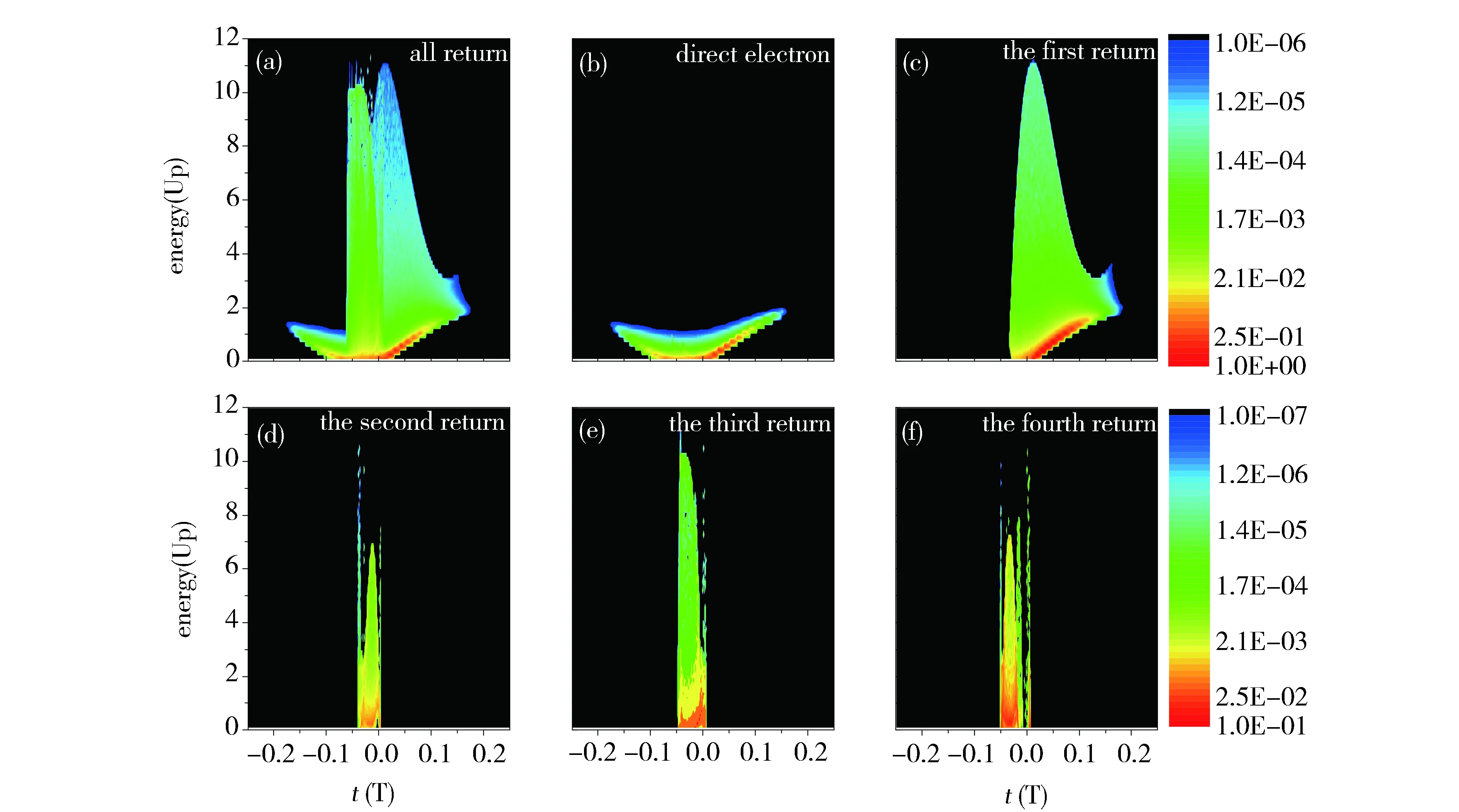
(a) all returns; (b) direct electron; (c) the first return;(d) the second return; (e) the third return; (f) the fourth returnFig.4 Tunnel time and energy distribution (a-f)图4 (a-f)为不同返回次数下的隧穿时刻与能量分布图

图4为氢原子在不同返回次数下隧穿时刻与最终能量二维分布图,横坐标是隧穿时刻,纵坐标是能量,不同颜色代表相对应的电离率。图4(a)为所有轨道的情况,可以看出分布虽然非常复杂,但是明显存在10 Up左右的截止。另外分布的极大值出现在隧穿时刻t=0附近,这是因为我们的计算中采用的是余弦电场,t=0时电场最大,隧穿率最高。我们将直接电离轨道以及不同返回次数轨道的贡献分开如图4(b)、(c)、(d)、(e)、(f)所示。图4(b)为被激光场加速而没有与母离子发生散射的直接电离电子的分布。可以看出其截止能量为2 Up,隧穿时刻有很宽的分布并且关于t=0对称。图4(c)为第一次返回轨道的分布,此时电子的最大能量超过了10 Up,其对应的隧穿时刻分布有一定的宽度,在t>0时刻的分布明显多于t<0的分布。图4(d)、(e)、(f) 分别为第二、三、四次返回轨道所对应的分布,其对应的能量截止位置与能谱一一对应。与第一次返回相比多次返回(第二、三、四次返回)的隧穿时刻分布要窄的多,并且在t<0时刻的分布明显多于t>0的分布,这表明多次返回轨道与一次返回轨道具有明显不同的特征。因此,虽然第一次返回轨道可以得到与实验一致的能量截止位置,但是在对高阶阈上电离进行细致的定量研究时,多次返回碰撞轨道的贡献是不能忽略的。

3 结论

本文利用半经典模型,考虑电子隧穿后离子库仑势对电子的作用,研究了氢原子在800 nm,1.3×1014W/cm2线偏振强激光下的阈上电离过程。我们计算了不同返回次数碰撞轨道的能谱、碰撞时刻分布及隧穿时刻-能量分布。通过分析发现多次返回碰撞轨道具有与第一次返回轨道明显不同的特征,并且对高阶阈上电离具有重要贡献。因此对高阶阈上电离进行细致的定量研究时,多次返回碰撞轨道的贡献是不能忽略的。