连续变量系统高斯态的量子关联

马瑞芬,齐霄霏

(1.山西大学 数学科学学院,山西 太原 030006;2.太原科技大学 应用科学学院,山西 太原 030024)

0 引言

量子信息理论的主要任务之一就是量化量子态的量子关联。量子关联是量子力学令人惊叹的特性之一,是量子信息理论的核心基础。在有限维量子系统,量子态除了纠缠这种较强的关联性,还相继定义了许多其它重要的非经典关联,如量子失协(QD)[1-4],测量诱导的非局域性(MIN)[5-7]和基于测量诱导的扰动(MID)[8],量子操控[9]等,得出了很多漂亮的结果。近年来,连续变量系统受到人们的广泛关注。Paris[10]和Adesso等人[11]各自给出了两模高斯态量子失协的定义,并讨论了它们的性质。 高斯态量子失协已被应用到量子密钥分配[12]等领域,引起了许多学者的广泛关注。其他高斯量子关联的结果, 请参阅文献[13-14]及里面的参考文献。

注意到, QD、MID与MIN等量子关联都是由局域测量定义的。此外,在量化量子关联中平均距离量的运用已被用于检测复合系统态的纠缠性等[15-16]。最近,Guo和Fan[17]利用平均距离定义了有限维系统中态的一种新量子关联, 并证明了只有乘积态不包含这种量子关联。

受该文的启发, 在文献[18]中, 作者类似定义了连续变量系统中两种新的量子关联, 并证明了两体高斯态ρ是乘积态当且仅当两种关联均为0;对两模压缩热态和混合热态, 证明了这两种量子关联是一致的, 并给出了它们的具体计算公式。本文的目的则是在此基础上, 进一步讨论这两种关联的性质, 证明了对于任意两模高斯态, 文献[18]中定义的两种关联都是一样的, 并探讨了其与纠缠性之间的关系。

1 预备知识

设ρAB是(m+n)模连续变量系统S(HA⊗HB)中的态。 若ρAB的特性函数χρAB(α)具有高斯形式, 即

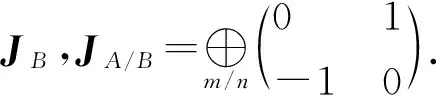
现假设ρAB是任意(m+n)-模高斯态，那么Γ可以写为

(1)

特别地, 当m=n=1时, 通过局域酉变换，Γ具有标准形式:

其中a,b≥1,ab-1≥max{c2,d2}.

(2)

此外, 当c=-d时, 两模高斯态称为压缩热态; 当c=d时, 两模高斯态称为混合热态。

(3)

其中λ∈[0,1],θ∈[0,π)与x∈[1,∞)分别代表压缩参数、旋转角度和温度。此外，ω是纯态种子当且仅当式子(3)中的x=1, 此时相应的{Π(α)}即为秩一测量。

2 连续变量系统的量子关联

文献[18]中引入了两种量子关联。

定义1 (文献[18]) 假设ρAB是(m+n)模连续变量系统S(HA⊗HB)的任意态。定义Q(ρAB)为:

其中上确界取遍系统HA上的所有GPOVMs

ΠA={ΠA(α)}，ρB=TrA(ρAB),p(α)=Tr[(ΠA(α)⊗I)ρAB]

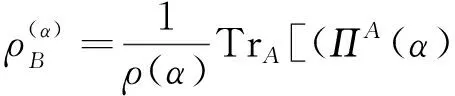
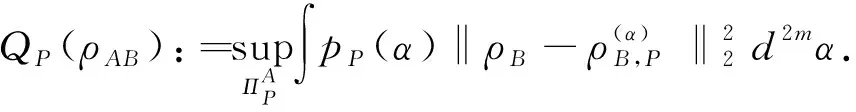
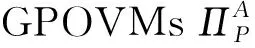
命题1([文献18,定理6]) 假设ρAB∈S(HA⊗HB)是两体(m+n)-模高斯态,其相关矩阵Γ具有等式(1)中形式，则

且

其中ΣA和ΣA,P分别是表示m模生成种子和纯态生成种子相关矩阵并且

YA=(ΣA+A)-1+(ΣA+A)-1C(B+Λ)-1CT(ΣA+A)-1，

并且ΛP,Np,YA,P与Λ,N,YA具有相似的形式。

文献[18]中的定理10表明, 对于任意两模压缩热态和混合态ρAB, 必有Q(ρAB)=QP(ρAB).一个自然的问题是, 对于任意两模高斯态, 这两个量子关联是否一样。 下面的定理说明答案是肯定的。 注意到，Q与QP均具有局域酉不变性[18], 因此可假设两模高斯态的相关矩阵具有标准形式。

证明对任意两模高斯态ρAB, 由命题1知

与

注意到单模生成种子的相关矩阵ΣA与ΣA,P具有等式(3)中的形式。 通过maple软件计算, 我们有

进而得到

其中

由文献[18]知, 只需证明c≥|d|时定理成立。

事实上,当c≥|d|时,容易看出,当θ=0时,f(x,λ,θ)取得最大值,即

(4)

因为f(x,λ,0)在区域{(x,λ)∈R2:x>1,0<λ<1}内没有内点, 所以上确界在边界处{x=1,0≤λ≤1}∪{x≥1,λ=0}∪{x≥1,λ=1}取得。此外,容易得出f(1,0,0)=f(x,0,0)对所有x≥1成立。因此有

(5)

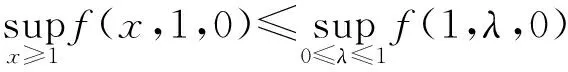
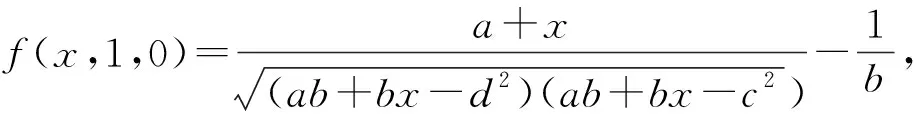
这意味着

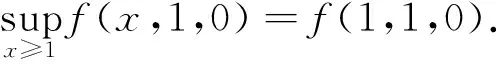
同理可得

最后, 利用函数f(x,λ,θ)的表达式, 可知定理成立。 证毕。

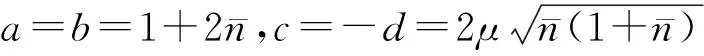
对SSTSρAB, 由文献[18]有

(6)

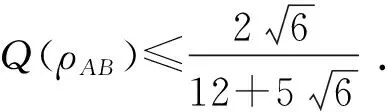
另一方面, 对于SSTSρAB,利用Williamson定理[22]知,存在辛矩阵S,使得其相关矩阵

(7)

其中v是ρAB的辛特征值。

对任意两模高斯态σAB,文献[23]给出了纠缠度(logarithmic negativity)的定义, 即

图1给出了Q(ρAB)与Ε(ρAB)之间的关系。从图1可以看出, 对于固定的纠缠度E,Q(ρAB)是其辛特征值v的增函数。

Fig.1 Quantum correlation Q(ρAB) of STS ρAB as a function of entanglement Ε(ρAB), in the plot, we have the curves with the symplectic enginvalues v=1,2,3,4,5 from bottom to top图1 图中曲线表示压缩热态ρAB的量子关联Q(ρAB) 作为Ε(ρAB)的函数图形,曲线从下至上依次代表ρAB的辛特征值v分别为1,2,3,4,5