带Neumann边值条件的p-Laplace方程组 径向增长解的存在性

张亚静，宣子娇

(山西大学 数学科学学院,山西 太原 030006)

0 引言

本文考虑以下椭圆方程组

(1)

其中,B是RN中单位球,ν是边界∂B上的单位外法向量,λ1,λ2>0,p-Laplace算子是二阶拟线性微分算子,定义为Δpu=div(|u|p-2u),p>1.众所周知,椭圆方程组有许多实际应用,例如种群进化,反应扩散问题,多孔介质等。近年来,拟线性椭圆方程组得到越来越多的关注,例如文献[1-11]及其参考文献。

(2)

Bonheure等人使用拓扑不动点理论证明了(2)径向增长解的存在性[4]。Ma等人在f,g不同的假设条件下通过全局分岔定理证明了径向增长解的存在性[16]。

基于文献[12，16-17]及其参考文献,我们研究方程组(1)径向增长解的存在性。目的是得到λ1,λ2以及一对函数(u,v)∈W1,p(B)×W1,p(B)使得(1)在弱的意义下有解。受文献[20-21]启发,我们使用变分法去证明问题(1)在无非线性增长性条件下正径向解的存在性。对照带Dirichlet边界条件的拟线性椭圆系统存在性结果,我们注意到在处理Neumann边值条件时,不是必须假设增长性来确保正径向解的存在性(例如次临界性假设)。据我们所知,目前对于拟线性椭圆方程组的Neumann边值问题研究很少,所有涉及拟线性椭圆方程组的研究都在Dirichlet边值条件下。本文将文献[16]和文献[20]的结果拓展到拟线性椭圆方程组。

我们作如下假设:

(H1)Q∈L1((0,1))是非常数径向增函数,对几乎所有r∈[0,1]有Q(r)>0;

(H2)H∈C1([0,+∞),[0,+∞)),H(u,0)=H(0,v)=0,Hu(0,0)=0,Hv(0,0)=0,在[0,+∞)上, ∀u>0,H(u,·)严格递增;∀v>0,H(·,v)严格递增;

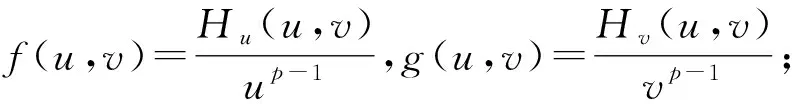
本文结论如下:

定理1 假设(H1)-(H3)成立,存在λ1,λ2>0,使得方程组(1)至少存在一个正径向对称的单调增长解。

推论1 对α,β≥1,α+β>p,Hénon方程组

(3)

至少存在一个径向增长解。

记号

·任意径向函数u记作u(x),x∈B,或u(r),r∈[0,1].

‖u‖Lp,p∈(1,+∞)表示函数u的Lp范数

·W1,p(B)是Sobolev空间, 范数:

·X=W1,p(B)×W1,p(B)表示Banach空间, 对应范数为:

1 非线性特征值问题

定义集合

M={(u,v)∈W1,p(B)×W1,p(B)|u(r)≥0,

v(r)≥0,u(r)≤u(s),v(r)≤v(s),∀r,s∈[0,1],r≤s}

径向函数u,v∈W1,p(B), 由于径向函数u,v在(0,1]连续, 且u,v为非负单增函数, 可定义

使得u,v在[0,1]为连续函数。解非线性特征值问题(1)即找变分问题(4)的解。

(4)

引理1 存在正常数CM使得‖u‖L∞≤C‖u‖,‖v‖L∞≤C‖v‖,∀(u,v)∈M.

证明证明过程可参考文献[20]命题1。

定义泛函I:M→R

由于M⊂L∞(B),H∈C1([0,+∞),[0,+∞)),∀(u,v)∈M,

H(‖u‖L∞,‖v‖L∞)|∂B|‖Q‖L1(B),

因此, 泛函I定义在M上,又因为H无增长性条件,I不能定义在整个W1,p(B)×W1,p(B)空间。

引理2S是一个有限正数。

证明设(u,v)∈M使得‖(u,v)‖p=1,由引理1,

H(CM,CM)|∂B|‖Q‖L1(0,1),

由S的定义,Q是严格正的且远大于零可知S是有限正数。引理2得证。

引理3 存在(u,v)∈M使得I(u,v)=S.

证明取序列(un,vn)∈M,使得∀n≥1,‖(u,v)‖p=1,I(u,v)→S.序列(un,vn)在W1,p(B)×W1,P(B)有界。

假设对子序列, 存在(u,v)∈W1,p(B)×W1,P(B), 有

在W1,p(B)中，un→u,vn→va.e. 在B上

由(un,vn)∈M得, (u,v)∈M.

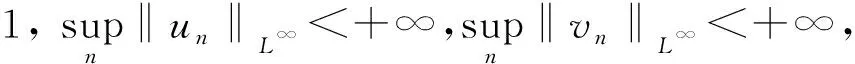
如果‖(u,v)‖p=1成立, 则S在(u,v)处达到。

下证‖(u,v)‖p=1.

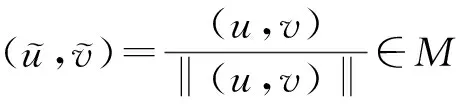
我们证明了S在(u,v)处达到, 接着证明(u,v)在弱的意义下是微分方程的解。

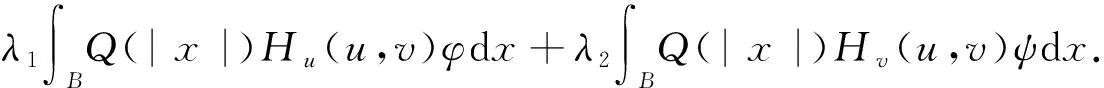
(5)

定义辅助函数G:[0,δ)→R

在ε=0时取最大值。 由‖(u,v)‖p=1,计算得

0≥G′(0)=

则

现在考虑下列两个问题

(6)

(7)

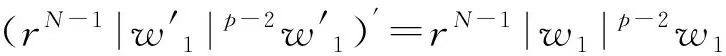
又w1是严格正的,故ω>0,即w1是严格增的,同理,w1也是严格增的,因此,w1,w2是正的径向增函数。

注:函数u,v是单调增的径向函数，满足u′(r)≥0,v′(r)≥0.实际上，u,v是严格增的。

证明对每个s∈[0,1],由于u,v,w1,w2均为正的径向增函数, 故u+s(w1-u)+,v+s(w2-v)+是径向增的，因此, (u+s(w1-u)+,v+s(w2-v)+)∈M.

由引理4, 我们有

(8)

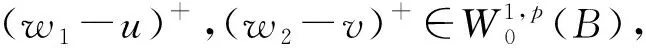
上面两式与(8)相减,

引理6 对几乎所有的r∈[0,1]，S的极大化(u,v)满足u′(r)>0,v′(r)>0.

证明这里仅给出u′(r)>0的证明。

取ρ∈(0,1),设δ>0,取适当的μ>0,定义连续函数ωδ:[0,1]→R,

则ωδ(r)∈W1,p(B)且ωδ是增函数。由于ωδ不是正的,故(ωδ,v)∉M.对每个正的足够小的s,有(u+sωδ,v)∈M.

由(5)得,在Lebesgue空间Lq(B),对q<∞,当δ→0+, 且

有,

(9)

因此,

类似地,

则在(9)式中, 令δ→0+,∀ρ∈(0,1),有

(10)

因此, 我们得到,

上面两个不等式至少有一个严格不等,否则,有

此时函数u,v是常数,Q也是常数。这与假设(H1)矛盾。

回到(10)式,我们证明了

(11)

(1+μ)ρN-1|u′(ρ)|p-2u′(ρ)>0,a.e.ρ∈(0,1),

又由于μ>0,故u′(r)>0,a.e.r∈[0,1]。 同理可证, 对几乎每个r∈[0,1],v′(r)>0.

现在证明极大化(u,v)是问题(1)的解。

引理7 对任意径向函数(φ,ψ)∈C1(B)×C1(B),S的极大化(u,v)满足

设χEk是集合Ek的特征函数, 取(φ,ψ)∈C1(0,1)×C1(0,1),定义两个函数

.对固定的k≥1,取ε>0,使得

对满足条件的ε, 有(u+εφk,v+εψk)∈M且u+εφk≠0,v+εψk≠0.对每个r∈[0,1],u(r)+εφk(r)≥u(0)-|ε|‖φ‖L∞>0,v(r)+εψk(r)≥v(0)-|ε|‖ψ‖L∞>0.对几乎所有的r∈(0,1),由φk(r),ψk(r)定义,我们有

(u+εφk)′(r)=u′(r)+εφ′(r)χEk(r),(v+εψk)′(r)=v′(r)+εψ′(r)χEk(r).

若r∈Ek,则

(u+εφk)′(r)=u′(r)+εφ′(r)χEk(r)>0,(v+εψk)′(r)=v′(r)+εψ′(r)χEk(r)>0.

若r∉Ek,我们有

(u+εφk)′(r)=u′(r)>0,(v+εψk)′(r)=v′(r)>0,

因此, 几乎处处有(u+εφk)′(r)>0,(v+εψk)′(r)>0,即u+εφk,v+εψk是严格单调增的。

由(5)式得

由于

由Ascoli-Arzelà定理, 在[0, 1]上,φk,ψk分别一致强收敛于φ,ψ。

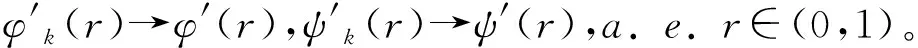
由于(φ,ψ)是任意的, 有

由此,引理7得证。

定理1的证明

由引理7可知, 根据稠密性,∀(φ,ψ)∈W1,p(B)×W1,p(B),

又由对称临界原理[22], (u,v)是问题(1)的解。