汽车顶盖失稳载荷规律数值分析

黄红端 朱灯宏 刘洋 韦超忠 黄金旺

摘要：应用有限元数值模拟法研究不同曲率半径顶盖及横梁高度对汽车顶盖屈曲失稳的影响。计算结果表明，顶盖失稳载荷与曲率半径成指数反比例关系;顶盖失稳载荷与横梁高度呈线性正比例关系。根据数值模拟结果得到了汽车顶盖失稳载荷与曲率半径、横梁高度之间关系的计算公式，为校核、计算汽车顶盖失稳载荷提供了参考。

关键字：汽车顶盖;曲率半径;顶盖横梁;失稳载荷;数值模拟

中图分类号：U463.82+1 文献标识码：A 文章编号：1005-2550（2018） 02-0072-04

引言

汽车顶盖作为整个车身最大的覆盖件，不但影响着整车外形美观，在保持车身结构，保护乘员安全、改善乘员NVH等方面同样起到重要作用。因此，汽车顶盖的结构稳定性在整车性能设计目标中具有非常重要的意义。国内外学者对顶盖结构模态性能、抗凹性能进行了一定的研究。本文文献采用薄壁腔体的屈曲应力的计算公式对汽车顶盖结构优化设计，并给出抑制薄壁腔体产生曲线现象的关键影响因素。文献采用综合评价方法结合有限元分析对轿车顶盖结构进行研究，系统评价了轿车车顶结构的静态、动态性能，并详细介绍了载荷、边界条件的设置等，给出了相应的评价准则及适用范围。文献考虑材料、几何和边界的复杂非线性以及模拟天窗的夹紧，用Abaqus有限元分析软件对某车型开天窗的顶盖的抗凹性能进行有限元分析，并通过试验验证了仿真分析结果。虽然前人对顶盖的抗凹性能进行了较多的研究，但是在顶盖失稳载荷分布规律及失稳载荷影响因素研究方面的相关文献很少。另外，顶盖生产、运输及返修过程中也容易造成局部区域出现凹痕情况。为此，本文运用有限元数值模拟方法研究汽车顶盖失稳载荷分布规律及顶盖不同曲率半径、横梁高度对汽车顶盖屈曲失稳的影响规律，可为车身顶盖结构设计和工程应用提供重要的理论依据。

1 基本概念与理论

屈曲有时也叫失稳，主要发生在细长或薄壁结构上，当施加在结构上的载荷达到某一临界值时，结构产生跳跃现象，构形将突然跳转至另一个随遇的平衡状态。屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷。

线性屈曲分析是以特征值为研究对象的，特征值方程决定了结构的分支点。进行线性屈曲分析的过程就是对相应矩阵方程进行求解，找到所求解结构的分支点，得出材料的屈曲因子λ_i和屈曲模态ψ_2i。

静力分析中刚度矩阵的应力状态函数为：

（[K]+[K_G]）{x}={P_ref}

（1）

如果分析是线性的，可以对载荷和几何刚度矩阵乘上一个系数，此时：

（[K]+λ_i[K_G]）{x}=λ_i{P_ref}

（2）

在屈曲模型中，当载荷达到临界值时，结构的位移会大于而载荷没有增加，即：

（[K]+[K_G]）{x+ψ_i}={P_ref}（3）

通过上面的方程进行求解，可得：

（[K]+[K_G]）{ψ_i}=0（4）

式中，[K]为结构的刚度矩阵;[K_G]为结构的几何刚度矩阵;λ_i为屈曲因子（参考载荷的放大系数）;{x}{ψ_i}为屈曲模态（位移特征向量）;{P_ref}为参考载荷（任意值）。

上式就是在线性屈曲分析求解中使用的方程，对于同一种材料，[K]和[K_G]为定值，通过对方程的求解，可以得到需要的屈曲因子九，和屈曲模态特征值ψ_i，则屈曲临界载荷可以根据下式计算：

P_Cr=λP_ref

（5）

其中，求解过程中得到的屈曲因子和屈曲模态特征值均为多维向量，但结构屈曲只与最小有關，因为一旦发生屈曲结构即失效。

2有限元分析

2.1几何模型

为了得到顶盖失稳载荷与顶盖曲率半径关系，文中顶盖X向曲率分别取4000mm、6000mm、8000mm、10000mm、14000mm、24000mm、34000mm、40000mm、44000mm、54000mm。顶盖Y向曲率分别取4000mm、6000mm、8000mm。为了得到顶盖失稳载荷与顶盖横梁高度关系，顶盖横梁高度分别取10mm、18mm、25mm、30mm。顶盖外板及横梁厚度为t=0.7mm。顶盖总成几何模型，如图1所示。

2.2有限元模型

本文采用有限元前处理软件Hyper Mesh进行网格划分，有限元计算模型如图2所示，共有单元33142个，其中壳单元为31748个，实体粘胶单元1394个。顶盖及横梁的材料特性：弹性模量为2.1×10⁵ MPa，泊松比为0.3，密度为7 850 Kg/m³。粘胶的材料特性：弹性模量为50 MPa，泊松比为0.49，密度为1200 Kg/m³。边界条件：约束顶盖总成四周X，Y，Z方向平动自由度。在顶盖外板表面各测点处施加1N的集中载荷，通过将载荷设置选项和分析类型设置为静载荷下的屈曲分析（buckling）来确定加载位置的失稳载荷。

根据汽车顶盖的结构特点可知，顶盖外板关于Y轴对称。考虑汽车顶盖特性及对称性，沿X向、Y向将顶盖外板4等分，取等分线交叉点作为测点，从左到右，从上到下进行编号，顶盖失稳载荷测点位置分布，如图3所示。

2.3顶盖曲率半径

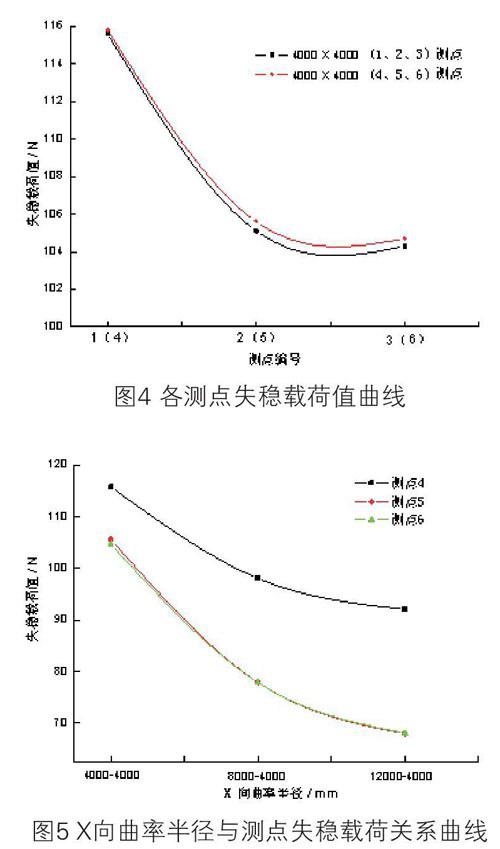
为了得到顶盖失稳载荷与顶盖曲率半径关系，首先需要得到顶盖外板各测点失稳载荷分布规律，再从测点失稳载荷规律中选取最具代表性的测点位置进行下一步分析。为了求得顶盖各测点的失稳载荷分布规律，对X向曲率半径为4000 mm，Y向曲率半径为4000 mm的顶盖进行数值模拟计算，得到顶盖各测点失稳载荷值曲线，如图4所示。从分析结果可知，测点4失稳载荷值最大，其次是测点1，测点3失稳载荷值最小，即越靠近前挡风玻璃顶盖越拱起的位置越不易发生失稳。同时，可以得到沿Y向分布测点失稳载荷值相差不大。

从图5、图6可知，X向、Y向曲率半径增加，各测点失稳载荷值减小。测点5与测点6失稳载荷值相差0.9 N，即越靠近车身尾部区域失稳载荷值越小且数值相差不大。

根据数值模拟计算结果，可以得到测点6顶盖失稳载荷与顶盖X向曲率半径的关系，其具体表达式为：

式中，F_collapsing（r）为顶盖测点失稳载荷，N;r为顶盖X向曲率半径，mm：

A₁、B₁和C₁为待定系数，见表1：

由式（6）可知，当顶盖曲率半径→+∞时，测点失稳载荷逐渐趋向于一个下限值，见图7所示。在顶盖曲率半径5000 mm至24000 mm之间，由于顶盖弧度变化比较明显，各测点失稳载荷变化比较急剧;但是，当曲率半径超过一定数值时，顶盖失稳载荷基本不随曲率半径变化。

2.4顶盖横梁高度

顶盖测点失稳载荷与横梁高度呈线性正比例关系，失稳载荷随横梁高度增加而增大。有数值模拟计算可以得到以下公式：

F_collapsing（h）= A₂+ B₂*h

（7）

式中F_collapsing（h） -含顶盖横梁测点失稳载荷，N;

h——顶盖横梁的高度，mm;

₂、B₂——待定系数，见表2：

表2不同测点位置时，式（7）中的待定系数

由表2数据可知，测点5与测点6斜率相差不大，且失稳载荷相差也不大;相对于测点5和测点6，测点4失稳载荷增加剧烈，见图8所示，其主要原因为：失稳载荷与顶盖横梁分布也存在直接关系，本文分析车型为MPV车型，相对于其他普通车型来讲，该车顶盖外板长宽比比较大，顶盖外

3结论

（1）通过汽车顶盖失稳载荷分析得到当顶盖曲率半径相同时，沿着+X向测点失稳载荷递减;顶盖对称轴沿Y向两边分布测点失稳载荷值相差不大。这主要是因为顶盖Y向曲率半径趋于无穷大时，顶盖趋于平面。

（2）通过取不同的X向曲率半径，分析得到頂盖失稳载荷与曲率半径成指数反比例关系。顶盖X向曲率半径5000 mm至24000 mm之间，由于顶盖弧度变化比较明显，各测点失稳载荷变化比较急剧。随着曲率半径增加，失稳载荷逐渐趋向于一个下限值。

（3）在相同的顶盖曲率半径下，顶盖失稳载荷与横梁高度呈线性正比例关系。失稳载荷大小与横梁高度及横梁X向分布位置有直接关系。