基于La-VaR模型互联网金融流动性风险的研究

陈耀辉 杨 宁

（南京财经大学，江苏 南京 210046）

一、引言

互联网金融的概念是由谢平于2012年首次提出，目前，互联网金融风险的分类形式多样，如市场风险、信用风险、操作风险、流动性风险、法律风险等。谢平认为，与传统的商业银行和资本市场不同，互联网金融是“第三种”金融模式，高速发展的背后所蕴藏的风险逐渐引起社会各界的关注。2014年政府首次将互联网金融写进工作报告；2017年，互联网金融第四次被写入政府报告，其中“控风险”成了该报告的主要基调和关键词。

近年来，随着金融行业以及互联网技术的飞速发展，互联网金融逐渐的进入人们的生活中。例如常见的网上借贷、网上支付，都属于互联网金融的范畴。互联网金融快速发展的同时，其中蕴含的风险就成为我们不可回避的话题。互联网金融依托传统金融，借助了先进的互联网技术，这就决定了互联网金融风险比起其他传统和新兴市场的风险更加难度量和管理。本文着眼于互联网金融的流动性风险，以中证互联网金融指数为样本，采用GARCH方法和极值理论POT的方法分别计算经流动性调整的VaR值。

二、文献综述

风险价值（Value-at-Risk）模型,简称VaR模型，自20世纪90年代被引入到风险管理中，已经成为金融机构和监管当局所广泛采用的风险度量和管理工具。传统的VaR模型包含一个隐含的假设，在固定的时间（及持有期，通常为一天）内，无论投资者持有的头寸规模如何，都可以以固定的市场价格完成。显然，这个假设并没有考虑到流动性风险。

关于流动性风险的定义和计量，虽然国内外学者不断进行研究，但即便在传统的金融市场也没有形成统一的定论，一直处于探索阶段。在市场微观理论中，资产的市场流动性定义为：在进行迅速大规模交易时，对资产价格影响很小的能力。对于互联网金融而言，更是容易出现交易违约的现象，其流动性风险比传统金融更加严重。Bangia等(1998)将流动性风险分解为外生和内生两个方面，提出了BDSS模型，首次对流动性调整的VaR进行了研究。Amihud(2002)等认为流动性衡量了规定时间内完成交易所花费的成本，或达成一个理想交易价格所需要的时间。Liu(2006)和Hasbrouck(2009)等流动性分为交易成本、交易速度、价格冲击三个维度。在国内的相关研究中，杨之曙和吴宁玫（2000）提出了交易金额、交易次数、换手率、价格的波动性、换手率等指标，认为也可以被用来衡量流动性风险。宋逢明、谭慧（2004）通过延长清算时间将流动性风险引入VaR中。

在计算互联网金融流动性风险时，本文将采用La-GARCH-VaR和La-POT-VaR模型，可以满足对尾部风险精确描述的要求。同时，本文还采用了返回检验方法对改进后的La-VaR模型进行了测试，使得模型结果更具有说服力和一般性。

三、La-VaR模型的度量

对于流动性指标构造，基于交易成本的流动性风险，主要通过价差指标来衡量，这也是衡量即时交易成本最重要的指标，包括买卖价差、有效价差、实现价差和定位价差。买卖价差是当前市场上最低卖价和最高买价之间的差额，是最基本的流动性度量指标，一般有两种计算方法:绝对价差和相对价差，绝对价差是指买卖价差的绝对值;相对价差是除去了价格变量之后的结果。收益率r采取对数收益率的形式，表达式为，Pt为当天收盘价，Pt-1为前一天的收盘价。设最高价为P1，最低价格为P2，绝对价差S=P1-P2,中间价格P0为(P1+P2)/2,相对价差rs=S/P0，由覃小兵（2015）在对中国股市流动性调整的极值风险测度中，在置信水平α下持有单位金融资产的La-VaR可以表述为：

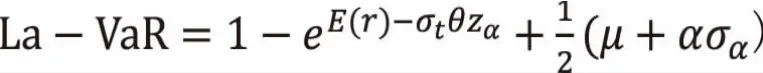
其中，E（r）是收益率的期望，σt是收益率的方差；θ是针对收益率序列的肥尾特征进行修正的调整参数，故有θ=1+φln(k/3)，k是对数收益率的峰度，φ取决于尾部概率。传统的BDSS模型假定收益率服从正态分布，并且买卖价差具有相同的方差，因此无法针对金融收益分布的尾部进行建模和分析，下面主要采用两种方法进行改进。

（一）GARCH模型

在进行短期预测时，可以使用ARMA模型，但无法处理金融时间序列存在的“波动率聚集”现象。GARGH模型由Bollerslev在1986年提出，该模型假定序列随机误差具有时变性，未来时刻预测值依赖于历史观测值在不同时刻波动程度有所差异，因而可以用来描述“波动聚集”效应。本文在ARMA模型中引入GARCH模型，ARMA-GARCH（1,1）形式如下：

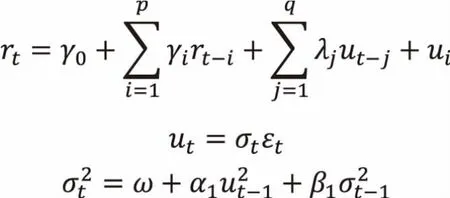
为扰动性，建模过程中假设其服从正态分布。

（二）极值理论

传统的BMM模型依赖于子区间长度的选择，容易忽略一些重要的数据，而阈值模型（POT）能够充分利用有限的观测值，为了在选这数据上弥补BMM模型的缺陷，该方法不是关注极值，而是着重讨论对某个高阈值的超出量和超出发生的时间。假设日对数收益率为r1,r2,...,rt,其分布函数为F(r),给定阈值为u,超出量为xi=ri-u,超出量x的分布函数表达式为

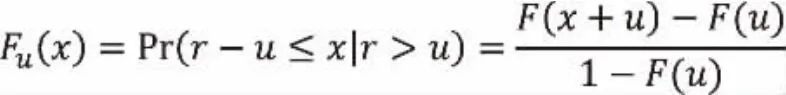
对于一个足够大的阈值u,Fu(x)可以由广义帕累托分布（GPD）近似表示，即 Fu≈G（x;ξ;β）,其中

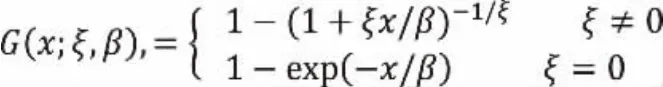
式中，ξ为形状参数，β为尺度参数。

记Nu为超过阈值的观测值个数，n为观测值数，日对数收益率r1,r2,...,rt的累计分布函数为

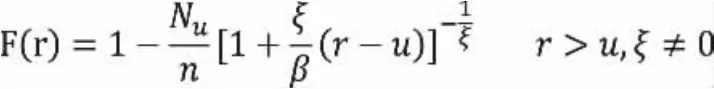
假设上尾概率为α，则F(r)=1-α。可以得出金融时间序列的(1-α)分位数，即

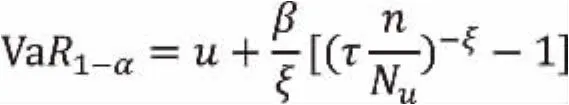
（三）模型的检验

返回检验是指通过VaR的计算结果来测试实际损失的覆盖范围，本文采用Kupiec提出的失败频率检验法。返回检验的方法是在实际损失大于估计的VaR时，记录失败；而把当实际损失小于估计的VaR时，成功被记录一次，并且失败的次数受二项分布的影响。假设返回检验样本数为T，其中失败次数为N(N≤T)，则失败率p=N/T。VaR模型的置信度为1-α，显著性水平为α，期望的失败率为p*=1-α。故VaR模型的返回检验对应着失败率p与显著性水平是否存在显著的差异。如果失败率p与显著性水平α之间没有显著性差异，则表明估计的VaR有效，反之则无效。原假设：H0=p=p*,Kupiec提出了基于失效率的LR统计量，表达式如下:

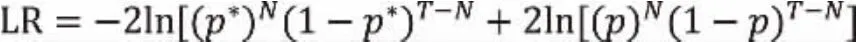
若原假设成立，服从χ2（1）分布。

四、实证研究

本文采用由中证指数有限公司于2015年2月10日正式发布的中证互联网金融指数来衡量我国互联网金融的发展状况。中证互联网金融指数（指数代码：399805，简称互联金融）是反应以互联网金融主题公司的整体表现的股票指数，具有权威性和代表性。

（一）数据选取与分析

互联网金融指数的样本空间为2012年6月29日至2017年12月29日，样本量为1342个，数据来自Wind数据库。由于本文是使用2018年1月2日至2018年4月18日的数据进行测试，因此样本长度为70。

表1 描述性统计检验结果

对样本进行单位根ADF检验，经检验该收益率序列不存在单位根的现象，是平稳序列。但序列存在显著的自相关现象，表现出了明显的“波动聚集性”。在对收益率r及相对价差rs的自相关性和异方差性进行研究时，本文建立ARMA（1,1）-GARCH(1,1)模型。在对收益率r和相对价差rs的调整因子进行估计时，可采用历史模拟法，99%置信水平下为2.7134，在95%置信水平下为2.0126。

（二）La-VaR及返回检验结果

模型假定，统计量LR服从χ2分布，其非拒绝域可表示为:

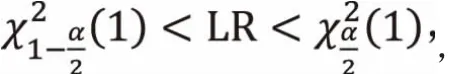
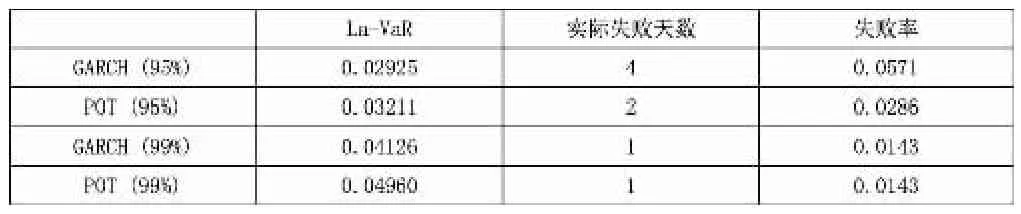
表2 互金指数La-VaR值及返回检验

可见，两种方法计算出的La-VaR值均落在非拒绝域内，并且用极值理论对流动性风险的衡量要优于GARCH方法。

五、结论

目前，计算经流动性调整VaR值的主要模型，Bangia等(1998)提出的BDSS模型依旧被众多学者引用，但是该模型本身存在许多不足，如假设价差波动同方差。针对BDSS模型的不足，本文引入Garch模型和极值理论来弥补BDSS模型的原假设：假定收益率服从正态分布，不能针对收益率分布尾部进行刻画。因此，改进后的La-VaR模型更能准确测度中国互联网金融面临的流动性风险，并且运用返回检验方法对模型的有效性进行验证，结果表明两个模型都能够显著地衡量流动性风险。

在改进后的La-VaR模型中，La-POT-VaR模型比La-GARCH-VaR模型不仅具有更好的覆盖能力，而且模型的失败率更低，从而使模型具有较强的有效性。虽然以GARCH模型为代表的参数模型能够反映金融时间序列的波动特征，但其更适合于收益率的波动较小的情况，在衡量具有较大波动特征的互联网金融收益率时，其精确性将会大大降低。因此，基于GARCH模型的VaR方法并不适合衡量互联网金融的风险。在度量中国互联网金融流动性风险时，本文提出的基于POT的La-VaR模型是一个较好的流动性风险度量模型，对于政府监管者而言，有效的控制互联网金融的流动性风险尤为重要，需要制定合理的监管机制，积极引导投资者进行理性投资，从而减少金融市场的盲目投机行为、缓解羊群效应，使得互联网金融市场有序健康的发展。