无反射板激光导航机器人地图创建的特征提取

李丹阳 张 轲 许如清 罗志峰 吴佳谦 桂 豪

1.上海交通大学上海市激光制造与材料改性重点实验室，上海，2002402.高新船舶与深海开发装备协同创新中心，上海，200240

0 引言

无反射板激光导航(自然导航)不需要设置繁琐的反光标识板，行走路径可根据实际需求随时改动，比有反光标识板的激光导航更加灵活,具有更低的人力和物力成本、更高的效率，代表激光导航技术的未来发展方向。无反射板激光导航最为关键的是地图的构建以及导航过程中对特征信号的准确识别和定位[1]。

真实环境的抽象描述称为地图构建。测距式传感器采集环境得到的数据是点的集合，如何处理这些离散的点获得环境的抽象描述呢？文献[1-3]详细比较了几种典型的数据点提取特征直线的方法：Hough变换法特征精度较高[4-5]，但计算量较大，难以保证局部地图构建的实时性；数据分裂与合并(split-and-merge)算法精度和实时性都较好[6-7]。

通常情况下，地图构建和导航定位提取的特征是直线或圆。直线是地图构建最典型的特征，本文采用逐步分解的方法，将直线特征提取分为断点检测、线段分割以及直线提取三个步骤逐步分离点集，来提高特征提取的精确度。

断点检测法有固定阈值法、自适应阈值法以及卡尔曼滤波断点检测法等[8]。自适应阈值法不受地图尺寸影响，且将点之间的关系纳入考虑范围，因此稀疏的线段不会被判定为断点。

线段分割的本质就是提取多线段中的拐点，目前较为成熟的线段分割方法主要有LT(line tracking)算法[9]、模糊聚类(prototype-based fuzzy)算法[10]和迭代适应点(iterative end-point fit，IEPF)[11-12]算法。

LT算法计算速度非常快且具有普适性，但难以确定一个合适的阈值，尤其在地图尺寸和误差量未知的情况下。此外，LT算法只考虑一个点的情况，而没有考虑所有已被纳入直线的点的残差，易将曲率较大的曲线误判断为直线特征。

模糊聚类算法的核心思想是通过递归计算，不断减小成本函数(cost function)来进行线段分割。模糊聚类算法有比较大的局限性，一是算法需要已知原型，采用模糊聚类算法必须把原型的数量作为已知条件，而在大多数应用情况下，线段的数量是未知量；二是模糊聚类算法容易受到异常值干扰，算法的鲁棒性差。

IEPF算法的核心是递归思想[11-12]，计算速度快且对局部地图的适应性好。

本文所涉及的环境为纺织仓库，环境特点以直线特征为主，因此对无反射板激光导航AGV地图构建的直线特征提取进行研究。针对环境地图扫描范围多变、扫描数据点远近稀疏不均，采用自适应阈值法进行断点检测，考虑到运算速度和局部适应性，采用IEPF算法进行线段分割，最后采用最小二乘法拟合直线及区域搜索法进行优化，进一步提高直线特征提取的精度。

1 实验系统及参数

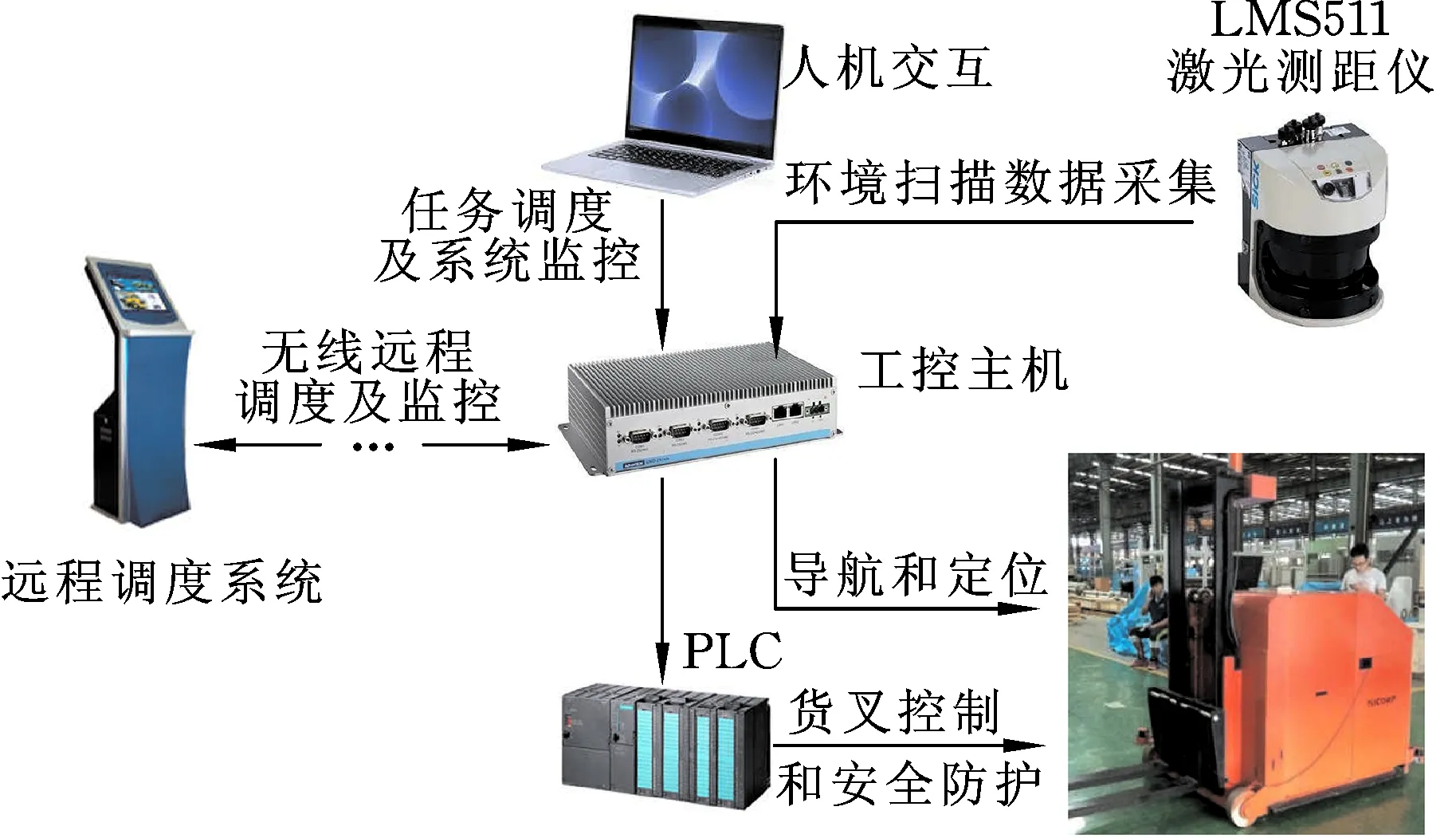
图 1 开发的无反射激光导航AGV系统架构Fig.1 Developed AGV architecture based on laser navigation without reflector

图1所示为研发的无反射板激光导航AGV系统架构。激光测距仪实时扫描外部场景并将数据传输给工控机；工控机进行地图构建、任务规划、导航，对搬运任务执行过程中的AGV进行实时定位，并将位置信息反馈给PLC系统；PLC主要完成货物的装卸以及安全检测和控制。通过远程调度系统(通过wireless signal 与AGV进行通信)对AGV进行远程调度。本研究中，激光测距仪为SICK公司的LMS511 2D型激光扫描测距仪，扫描频率为50 Hz，扫描角度范围为180°，每0.25°扫描一次，扫描高度为2.5 m。一次扫描后得到721个极坐标系下的数据点。

2 特征直线提取

2.1 自适应断点检测

在激光扫描地图匹配中，断点指在连续的扫描点中数据特征出现突变的情况。这种情况通常对应被扫描区域内的物体边缘、门、窗，或者环境中的障碍物等物体不连续的部分。断点检测是地图特征提取中非常重要的一个步骤，有助于辨识环境地图中的门、窗、立柱等重要的特征，方便随后的地图匹配以及路径规划等。

为方便问题描述，下文将连续的2个点统一命名为Pn-1、Pn，旗标Kn-1和Kn表征Pn-1和Pn是否为断点。如果Pn-1和Pn不连续，则Pn-1和Pn的对应值都被赋值为TRUE。

自适应阈值的判定标准：若|Pn-Pn-1|>Dmax，则判定Kn-1和Kn为TRUE。本文采用MORAVEC[8]提出的一种自适应阈值算法，原理如图2所示。首先假设一条通过Pn-1点的直线l，并假设这条直线是能被算法提取的最极端的情况，以此来外推最极端可接受情况下Pn点阈值圆的半径。直线l与Pn-1点的激光入射线Φn-1的夹角为λ，根据图2所示的几何关系可得

(1)

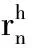
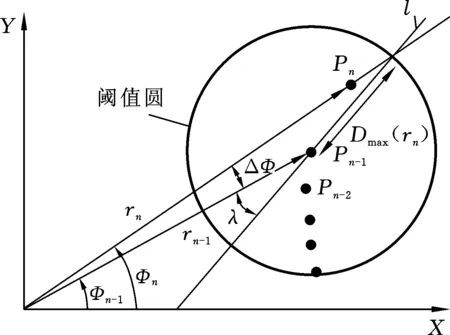
图2 自适应阈值的原理图Fig.2 Schematic of adaptive detection

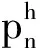
(2)

(3)

式中，σr为设定的传感器的测量误差，根据实际测试情况进行确定。

测试发现，在σr取25 mm，λ取5°的情况下，可以取得比较理想的结果。

自适应阈值法不受地图尺寸的影响，而且自适应阈值将点之间的关系纳入考虑范围，因此稀疏的线段不会被误判为断点。

2.2 线段分割

2.2.1点集分离

断点检测后，需先将点群按断点分为不同的点集，然后再进行线段提取。有效的特征直线应满足以下几个基本条件：①线段的长度应该超过最小值Lmin；②线段所包含的点的数量应该超过最小值Nmin；③不能有断点。因此，按这三个原则根据断点分离成不同点集，为后续进一步的线段分割奠定基础。

2.2.2迭代适应点算法

IEPF算法利用递归的思想，不断地将点集P={Pni,Pni+1,…,Pne}划分为子集P′={Pni,Pni+1,…,Pna}、P″={Pna,Pna+1,…,Pne}。如图3所示，首先连接起点Pni和终点Pne，得到线段l，然后计算点集P中所有点到线段l的距离，将距离线段l最远的点标记为Pna，最远距离记作Tmax。然后将点集P按顺序从Pna处划分为子集P′和P″。划分将一直迭代，直至子集P′和P″满足了两个终止条件之一：①点集中的点的数量小于阈值Nmin；②Tmax的值小于阈值Tthreshold。

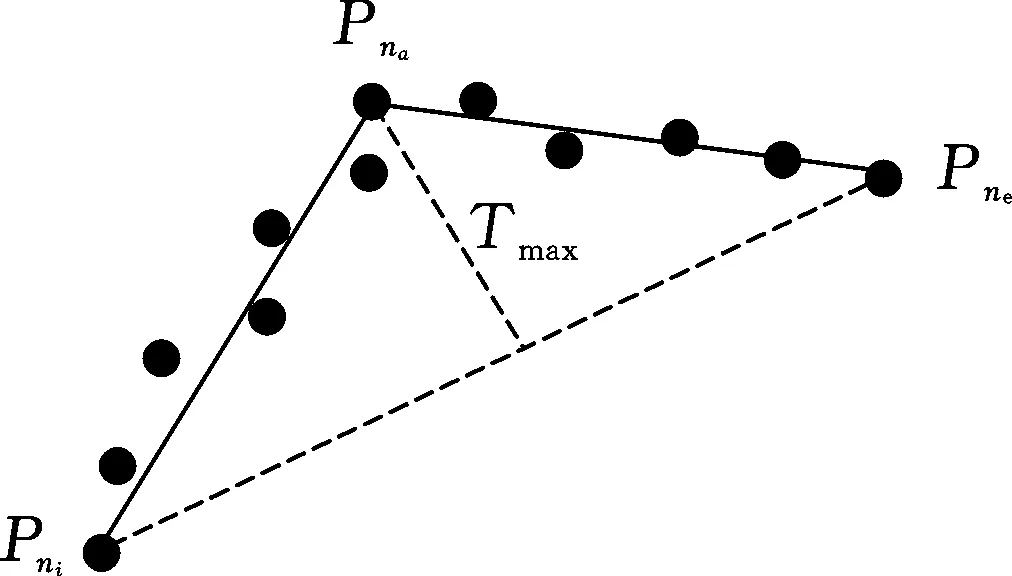
图 3 IEPF算法原理Fig.3 Scheme of IEPF algorithm

2.2.3算法实现

算法的主程序部分负责控制迭代的进行，并记录一轮迭代后所输出的拐点索引值。初始的搜索范围是整个点集，然后开始进行迭代计算，每一轮迭代后，输出下一轮的搜索列表和本次迭代后所得到的拐点。计算一直循环进行，直到某一次迭代后输出的搜索列表为空，这意味着点集中所有的分段都已满足上文所说的终止条件之一。最后的输出将包括所有拐点的索引值。具体过程如下：首先计算点集中所有的点到直线的距离，求其中的最大值Tmax以及对应的索引值(记为Pspinodal)。如果Tmax大于所设定阈值，则Pspinodal被判定为拐点，并将点集P分割为P′和P″两个子集。然后创建下一轮迭代的搜索列表。根据子集P′和P″内点的数量判断搜索列表函数，如果子集P′或P″点的数量大于阈值Nmin，则将子集P′或P″加入下一轮迭代的搜索列表；如果Tmax小于所设定阈值，则意味着点集P′或P″无需再分割。

2.3 特征直线提取及优化

线段分割后，在断点和拐点之间还有一些离散的点，它们不具有线段的特征信息。直线拟合的本质就是确定直线的参数特征，即将前文中所提取的断点和拐点所夹的中间点直线拟合为y=kx+b的形式。除了Hough变换算法，其他算法得到的线段分割结果都为点的信息，都需要进行直线拟合，本文采用最小二乘法进行特征直线提取。

直线拟合的过程将前文提取的结果(断点和拐点)有机地结合在一起，生成用于直线拟合的点集，即两个断点间以拐点为分割点的子集。程序首先尝试拟合直线，如果拟合残差超过设定的阈值threshold，需再进行拟合优化。直线拟合的关键算法如下：

/*生成直线拟合的点集*/

fitting_point = [ni sort(Pspinodal) ne]

for i in fitting_point do

/*尝试拟合直线*/

[parameter(i) error_value(i)] = LineFit (fitting_point)

/*当拟合残差超过阈值*/

if error_value(i) > threshold do

/*进行拟合优化*/

[parameter(i)] = LineFitOptimization (fitting_point)

end

end

进行拟合优化的原因是某些直线的拟合结果不理想，由IEPF算法的自身缺陷所致。图4是IEPF算法所导致的缺陷示意图，P1为程序所计算出的拐点，而P1(3 349，2 175)(mm)与P2(3 417，2 177)(mm)之间的距离仅为32 mm，Tmax小于两点之间的距离，远小于所设置的阈值75 mm，导致程序无法判定P2为拐点。减小阈值有利于程序识别P2为拐点，但阈值设定过小(在本例中，小于30 mm)时，迭代适应点将陷入时间复杂度为O(n2)的最糟糕情况，导致程序进入长时间的迭代。因此图4所示的缺陷情况难以通过改进IEPF算法加以改善，而应通过拟合优化的方式来解决。

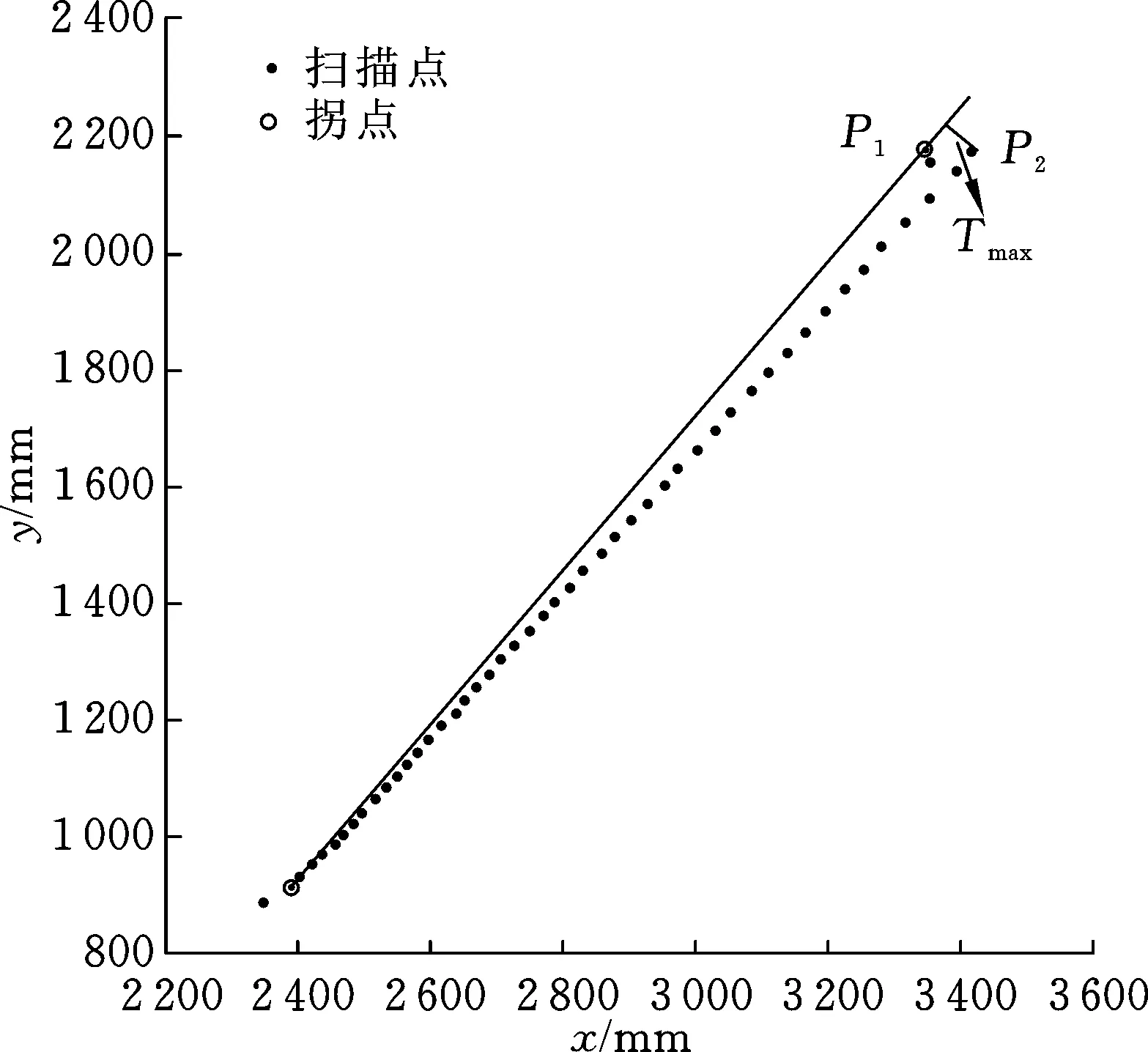
图 4 IEPF算法所导致的缺陷示意图Fig.4 Scheme of the defects caused by IEPF algorithm

优化拟合的思路如下：由于该缺陷一般仅出现在线段起点Pni或终点Pne附近，因此只需考虑在两端小范围内搜索从而寻找最优值即可。在本研究中，将搜索范围限定为[Pni+3,Pne-3]可以取得比较理想的结果。

算法如下：首先创建一个搜索列表；然后计算不同组合情况下的拟合残差，并以矩阵的形式储存；最后，求出最小残差及其对应的起点和终点的索引值，并输出此条件下的最优参数。

拟合优化的关键算法如下：

Function [parameter] =LineFitOptimization (fitting_point)

/*设置搜索区域*/

search_area = CreatSearchArea(fitting_point)

/*计算不同组合下的拟合残差*/

error_value_matrix = LineFit(search_area)

/*求最小残差对应的索引值*/

[error_value_min index]= min(error_value_matrix)

/*输出最优的参数*/

parameter = fitting_point(index)

3 结果和讨论

3.1 算法结果讨论

为验证特征直线提取算法的有效性，使用移动机器人在某厂的纱包仓库进行环境扫描、特征提取和地图构建测试。测试场景如图 5所示，仓库宽约20 m，长约110 m(图示长约60 m)，图中两侧的立柱、支架等以直线特征为主，可作为特征标识物方便定位。首先沿着预先规划的路径移动机器人，用激光测距仪扫描环境，进行特征直线提取、地图构建。分别对本文提出的自适应断点检测、IEPF线段分割、最小二乘法特征提取及优化算法进行测试和效果验证。

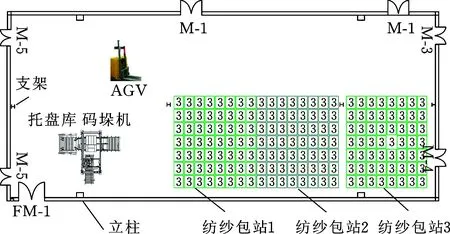
图 5 纺织车间纺织包堆放仓库应用场景Fig.5 Warehouse for textile spinning package

由图6可知，采用自适应阈值法可以比较理想地进行断点检测，在线段上的点排列稀疏程度不同的情况下，自适应阈值法都能成功识别出断点特征。

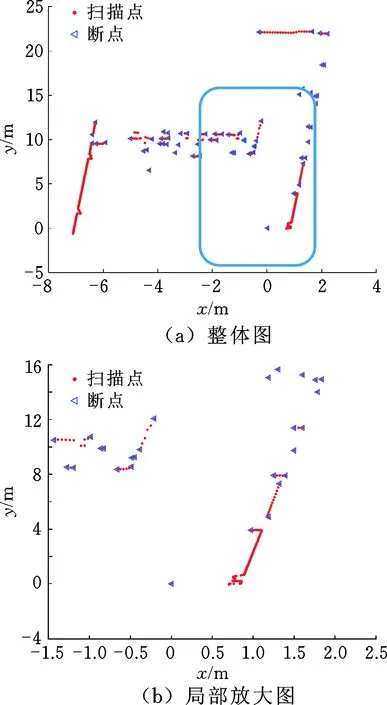
图 6 自适应阈值断点检测实例(σr=25 mm，λ=5°)Fig.6 Breakpoint detection used by adaptive thresholds(σr=25 mm，λ=5°)

图7所示为采用IEPF算法进行线段分割的实例。可以看出，该算法的效果较理想，可以精确地提取出一些非常细节的拐点，这非常有利于后续的特征提取和地图匹配。

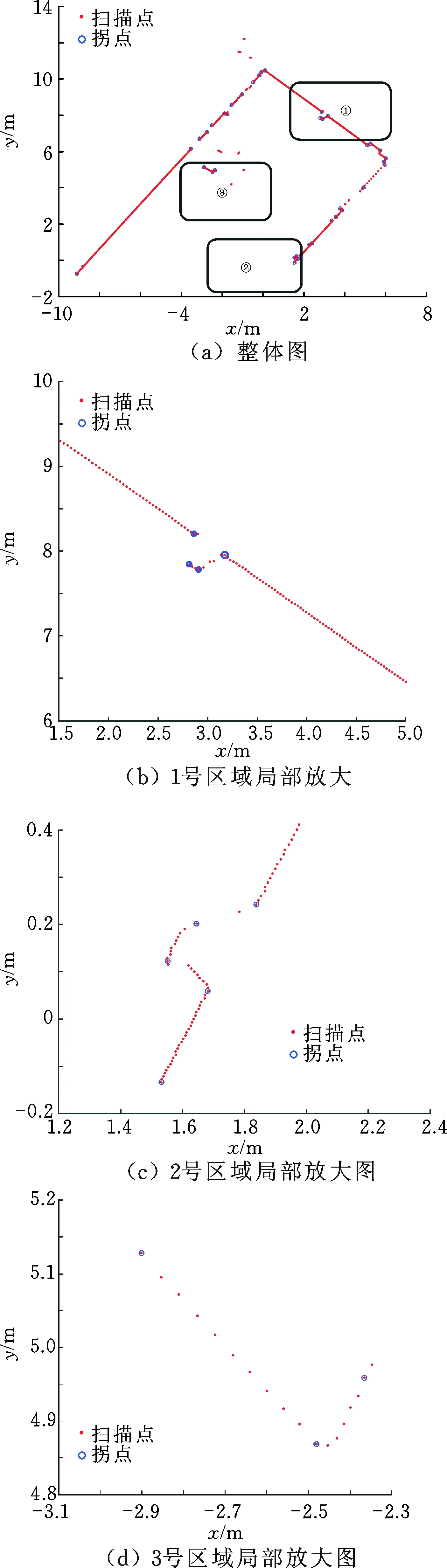
图7 IEPF算法线段分割实例Fig.7 Line segmentation based on the IEPF algorithm

实验中，采用IEPF算法的运算时间小于0.02 s，满足AGV在行驶过程中实时定位的速度要求。

图8所示为应用上述的断点检测、线段分割和线段拟合算法的直线特征提取实例，程序一共提取出12条直线特征，地图中主要的直线特征都被准确提取，尤其是在一些细节处的直线提取也得到了理想的结果。

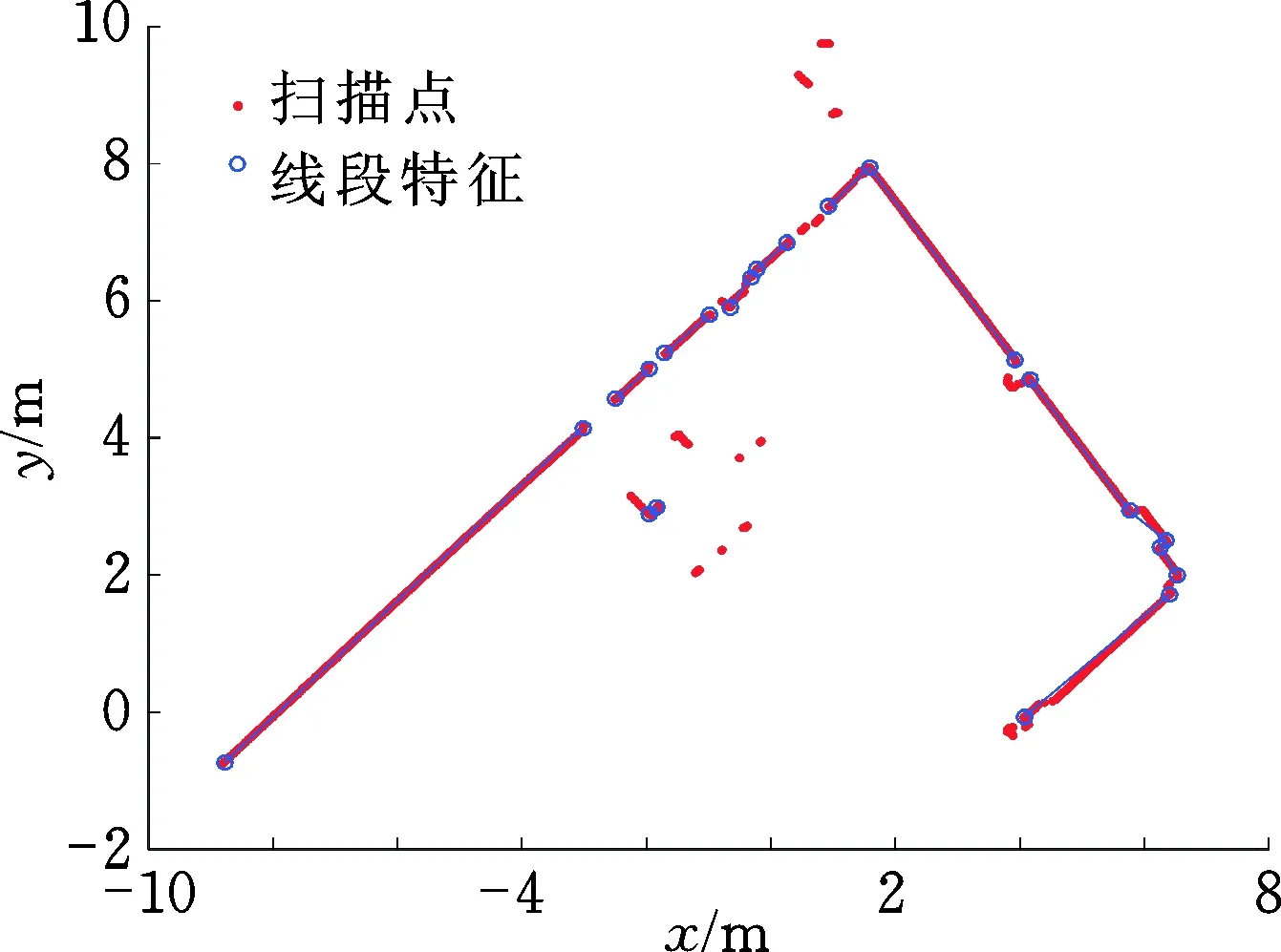
图 8 直线特征提取实例Fig.8 Line extraction by using least square method

图9是进行直线拟合优化前后的对比图，可以看出，优化过程可以使地图的直线特征提取更为精确。这说明由IEPF算法所引起的缺陷可以通过优化拟合过程得以消除。

拟合优化就是将拟合残差的影响纳入直线特征提取的考虑范围。经过断点检测和线段分割的步骤后，原先接近千个数据点集被算法简化为由断点和拐点组成的简单拓扑关系，所包含的信息量急剧减少，这虽然减轻了计算机的运算量，但增加了程序整体的盲目性。一旦断点检测和直线分割的算法出现遗漏断点或拐点的情况，程序将忽视原始点集而提取出地图上并不存在的直线。因此，在直线拟合的步骤中加入优化程序是十分有必要的。

3.2 重复定位精度测试

应用本文所提出的算法进行特征直线提取，然后进行地图匹配和构建，建立全局地图。将激光导航机器人移动到测试仓库的任意位置，并采用激光导航仪进行扫描，建立局部地图并将其与全局地图进行匹配，确定机器人的当前位置。在应用场景中任取了6个点进行重复定位精度测试，每个位置进行多次重复扫描。其测试结果如表1所示，由测试结果可知，X方向、Y方向的定位精度在±6 mm以内，而方位角的定位偏差则在±0.007 rad以内。

图10所示为表1第一个测试位置经过260次重复定位测试时的位置和方位角的变化。

由图10可知，X方向和Y方向的偏差始终在±6 mm以内，方位角变化始终在±0.003 5 rad以内，即使考虑小车在运动过程中产生的偏差，其整体偏差也可控制在±10 mm以内，该定位精度满足纺织纱包搬运重载机器人实际应用需求。

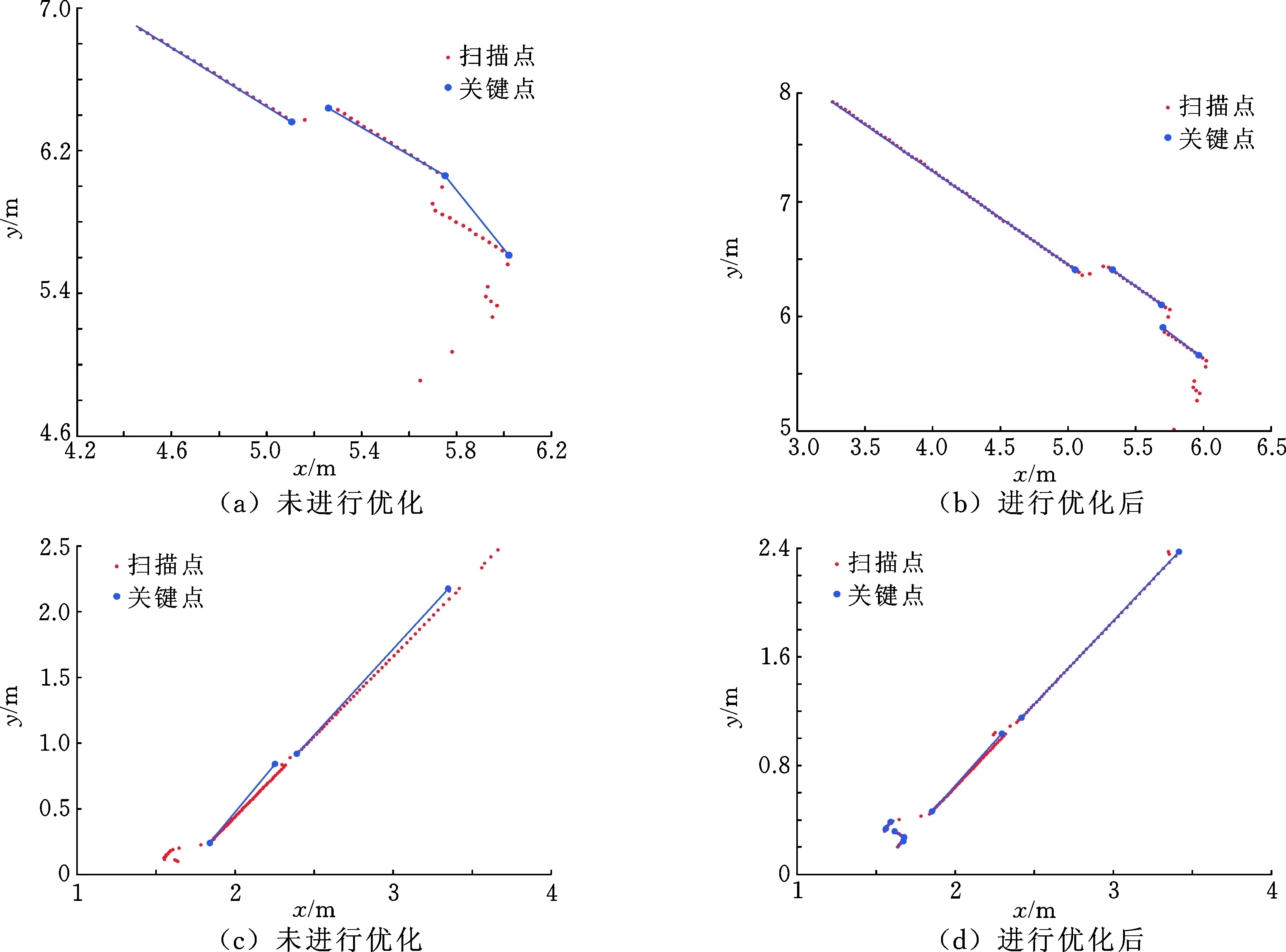
图9 直线拟合优化前后对比Fig.9 Comparison of line fitting before and after optimization

位置(x,y,θ)(xmax,xmin) (mm)(ymax,ymin) (mm)(θ max,θ min) (rad)重复次数(-6.00,15 326.0,0.08)(-13.2,-0.6)(15 322,15 332)(0.080 7,0.087 3)260(186.4,12 869.0,0.100)(180.2,193.4)(12 865,12 875)(0.099 1,0.104 1)120(54.90,15 249.0,0.06)(50.8,59.5)(15 245,15 254)(0.061 7,0.065 7)120(225.0,19 810.0,-0.030)(219.6,231.4)(19 807,19 815)(-0.029 4,-0.034 4)120(2 120,16 215.0,1.569)(2 114.9,2 124.6)(16 209,16 220)(1.566,1.575)120(-1 620,22 320,-1.568)(-1 625.2,1 615.6)(22 315,22 326)(-1.573,-1.563)120

图10 位置和方位角的变化Fig.10 Variation of the position and orientation angle

3.3 现场应用测试

将上述特征直线提取算法以及地图匹配算法等植入无反射板激光导航自主运动机器人，进行实际搬运任务测试。首先，激光导航仪扫描放置纱包的仓库，建立全局环境地图，机器人根据搬运任务规划运动路径。运动过程中，激光导航传感器实时扫描现场场景，提取特征直线后，创建当前位置的局部地图。AGV通过与全局地图中的期望位置相比较不断调整运动路径，这个过程被反复进行，直到搬运任务完成。图11所示为实验场景，纺织纱包被准确地取货，行进之后，在正确的位置放货。实验结果表明本文的算法满足实际应用要求。

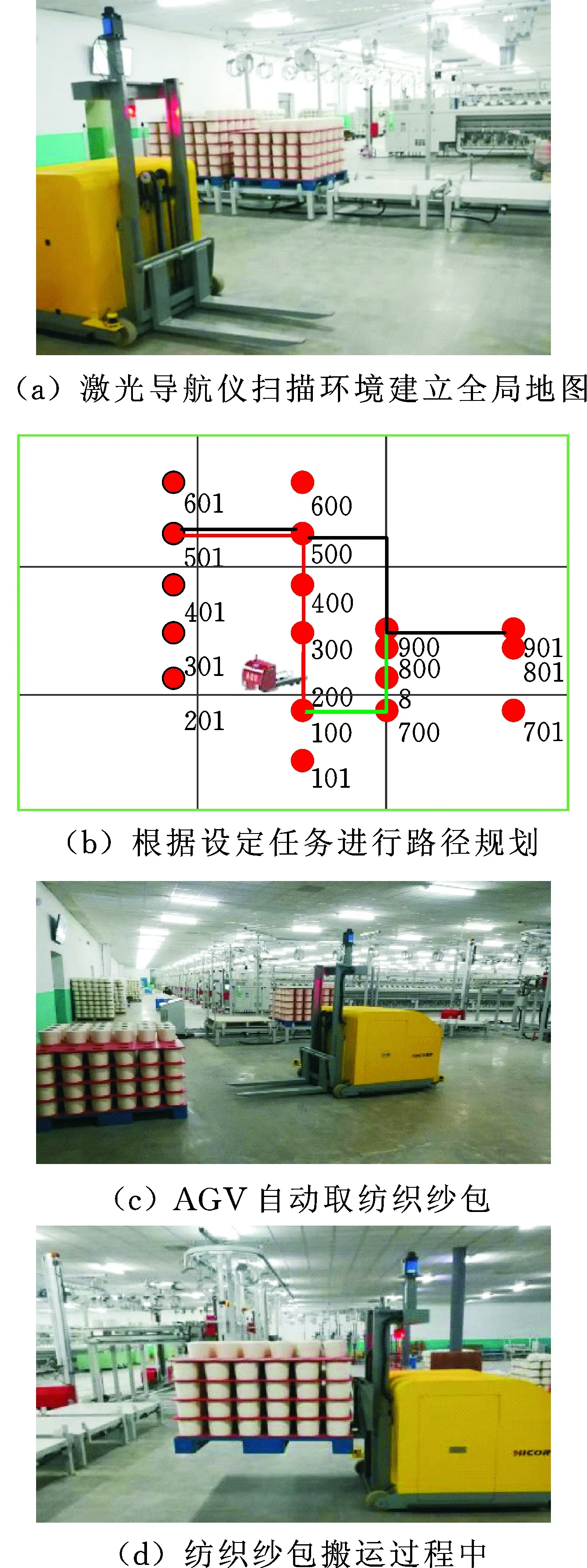
图11 开发的AGV搬运纺织纱包实验Fig.11 Experiment of carrying textile spinning package for the AGV

4 结论

(1)针对特征直线提取，提出了逐步分解的方法，将直线特征提取分为断点检测、线段分割以及直线提取三个步骤来分离点集。

(2)在断点检测部分，提出自适应阈值断点检测法。针对线段分割，提出的IEPF线段分割方法运算快且效果较好。

(3)对最后分离的直线特征点集，采用最小二乘法并结合局部区域搜索的方法进行直线特征提取，提高了精度并消除了线段分割中IEPF算法自身缺陷带来的不利影响。

(4)实验结果表明，所提出的逐步分解的直线特征提取方法可以精确地提取直线特征，位置重复定位精度在±6 mm以内，方位角偏差在±0.007 rad以内，计算时间在0.02 s以内。现场应用测试表明该算法满足大部分以直线特征为主的工业应用场合。