考虑不确定度的POT模型在洪水重现期分析中的应用研究

吴 迪

(辽宁省沈阳水文局，辽宁 沈阳 110094)

随机性和确定性方法为工程水文分析计算的两种主要方法，采用数理统计外推法并依据实测或水文历史数据可对重现期的洪水量值进行求解的方法为随机性方法；而确定性方法主要是对洪水灾害利用物理模型与数学工具进行反演模拟的方法。AMS年最大值法因其具有的理论系统成熟、计算概念清晰等特点被广泛引用于国内的水文统计计算中，而在实际工程应用中该方法仍存在诸多的问题和限制。数据观测年限的选择是确保计算结果可靠性的主要影响因素，通常情况下数据观测年限应不低于30年并因此造成该方法在资料匮乏区域的应用存在一定局限，即使可依据有关技术规范采用延拓或插补的方法对缺失数据资料进行补充，但依旧可对洪水的预测分析带来较多的不确定性。而且，对于有效水文信息或丰水年有价值的洪水数据利用年最大值法也存在丢失的现象，尽可能的获取样本值信息基本原则与采用年最大值法具有的特征现象明显不符。

国内外水文学者经过多年的努力和研究，分别利用多种理论和方法从各个角度提出了扩充样本法，而POT超阈值模型为水文研究最为常用的方法。对于水文事件POT模型将其认为是一个离散随机发生的过程，模型对统计分析的有效样本选取为超过某一洪水阈值的极值数据。对于实测数据中的有价值的数据该方法可最大程度的提取和挖掘，对其频率计算结果的精度POT模型可利用增大统计分析样本数量进行提高。Pickands等[1]研究表明，超出阈值的样本序列在阈值选取足够大的条件下满足GP广义帕累托稳定分布。Lang等[2]对POT模型拟合优度检验及其可靠性进行研究分析，并对POT模型采用GP分布时的频率与阈值之间的作用关系以及典型问题进行了探讨和分析，指出数据年限长度的2～3倍为合适阈值选择的适用范围；王建峰等[3]为提高计算精度提出了改进的线性矩法，并认为相对于传统的Pearson-Ⅲ型分布三参数GP分布的经验频率点与理论频率曲线在重现期较大时的拟合结果更优；张丽娟等[4]对POT模型计算结果受历史洪水数据的作用影响进行了探讨，并指出相对于AMS方法利用POT方法的拟合优度更佳。

多种复杂环境因素的共同作用形成的洪涝灾害其频率计算不仅与参数估计方法、统计分布函数等因素相关，而且受自然环境的变化、观测时间以及数据量的多少等客观因素的作用影响，超越预期的极端洪水事件在目前人类活动影响显著、全球气候变化剧烈的大背景下而经常出现，因此对计算成果的不确定性进行合理考量，在保证设计成果处于一定的安全状态并预留充足的裕度空间方面具有重要作用[5- 8]。据此，国内外学者对多种理论方法分别从不同的角度进行了研究，其主要集中在对模型参数的不确定性估计方面即通过设定合理的置信区间对参数估计的误差进行不确定程度的表征。本文以辽河流域为例，并依据流域出口断面流量数据资料，利用GP分布理论构建POT模型并对模型的置信区间范围及似然函数进行求解，对水文频率计算结果与不同观测年限样本数据之间的作用关系和影响规律进行探讨分析，并在此过程中对适线结果的拟合优度和样本的一致性检验、POT模型阈值选择原则加以探讨。

1 基本理论

1.1 统计分布函数的确定

样本序列{Xi}符合独立同分布基本特征，若固定值u满足Xi>u条件，则称x-u、u分别为超阈值和阈值，可采用下述公式代表样本序列平均超出量函数：

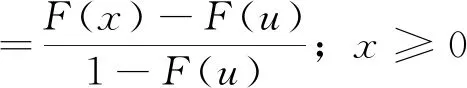
(1)

可利用下述函数代表三参数GP分布函数：

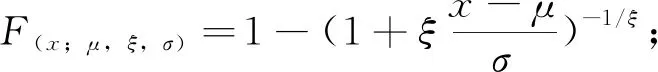
(2)

式中，F(x)—不超越概率分布函数；μ、σ、ξ—分别代表位置参数、尺度参数和形状参数。

依据上述计算公式，当样本数量足够大时采用POT抽样法获取的样本其GP分布函数可进一步简化为：

(3)

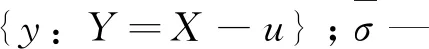
在时间段w内样本序列可利用POT模型进行筛选和证明，不难发现样本符合典型的HPP齐次泊松过程并且其速率为λw，而且在相邻时间间隔内的洪水发生时间符合指数分布特征。洪水实测数据在实际应用中往往可划分为多个固定时段，若超过阈值的洪水年平均次数为λ且洪水重现期为T年，则1/(λT)即可代表洪水的发生频率。可采用下述公式进行POT模型的洪水重现期的计算和求解：

T=1/λ(1-F(x))

(4)

式中，F(x)—代表GP的分布函数；T、λ—分别代表重现期和超越阈值速率。

可采用修正后的期望值公式对符合超阈值相似经验频率进行求解，其表达式如下：

Pc≈i·λ/(N+1)

(5)

式中，Pc—超阈值样本经验频率；i—按照降序排列的超阈值样本的序号。

1.2 参数估计与分位点估计方法

对模型参数利用极大似然原理进行统计估计的方法即为最大似然法，其常用的枉法为点估计法，其基本内涵为对模型最优参数利用目标函数的求解进行估计和提取。依据公式(4)可知，对重现期水平利用GP分布进行求解时不仅要对形状ξ和尺度σ参数进行估计，而且需对超阈值速率λ进行统计估计。结合文中所述，齐次泊松过程为洪水超阈值发生次数的分布特征，所以不仅要采用密度函数乘积基本方式而且对最大似然目标函数还需要考虑泊松分布函数基本理论，因此所建立的似然方程其表达式如下：

(6)

依据上述公式基本形式可对其进行推导，并且固定时段选取自然年长度其函数表达式如下，当ξ不为0时：

(7)

当ξ不为0时：

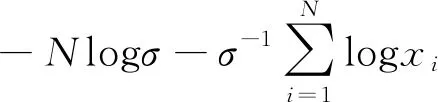
(8)

式中，N、w—分别代表超阈值样本总数和时段长度，其他各参数同上。

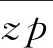
(9)

(10)

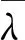
1.3 确定置信区间

依据待估计量的渐进正态性基本假设对置信度利用Delta法进行计算，即对分布函数相关参数置信区间采用Taylor展开式进行计算获取，可采用下述公式表征GP分布置信区间边界条件：

(11)

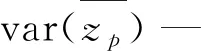
2 统计建模

2.1 区域概况

辽河流域位于我国东北地区西南部，属于温带、寒温带大陆性季风气候，冬冷干燥漫长，夏季多雨炎热，全年降雨量和流经量分布不均匀，其中西部径流面积较大，每年的7～8月为降雨旺季。流域内地势结构由东南向西北方向逐渐降低，海拔最高处为1800m最低处约200m。流域内工业发展充分、畜牧业和农林业发展迅速，不仅是我国的粮食基地也是工业发展中心[9]。辽河流域上游保存有较为原始的自然生态环境，所以对该流域所提取的实测水文数据资料具有一定的合理性和代表性[10]。本文统计整理了辽河流域1960—2010年出口水文站的实测日流量数据并将其划分为30、35、40、45、50年5种不同时长序列数据，对不同时长数据的选取对计算结果的不确定性影响利用模型进行探讨和分析。

利用模型进行极值统计分析时不仅要避免所提取的数据的自相关性，而且还要需保证各样本的独立性和数值的大小。针对上述问题国内外学者分别提出了多种判别标准并可独立次洪过程进行分割判别，限值法即对流量限值依据实测洪水数据变化状况进行估计，并对超过该限值的洪峰流量进行提取，该方法较为简便但可出现对前后相继的次洪过程进行阶段和忽略一部分小洪水事件等现象，据此本研究为获取独立洪峰数据值可利用该方法进行求解和提取[11]。

2.2 确定阈值

设定一个恰当的阈值u为POT模型统计计算极值洪水样本的核心和关键内容，如阈值选取的过大或过低将直接影响到有效样本数量的多少，阈值过低则对极值分布的基本含义相偏离，并可造成抽样数量的增大。相关学者针对样本选取方法开展了大量的研究，然而国内并未形成较为系统成熟的标准，其中年均超阈值发生次数法、分散指数法以及超阈值样本均值法等为较为常用的方法，其中超阈值样本法应用较为广泛并取得了很好的效果。Coles等[12]依据相关研究成果认为形状及尺度参数、尺寸区间应在合适的阈值作用下呈现出稳定线性状态，尽量选择稳定区间内较大的阈值并以此对极值样本进行筛选。本文依据上述过程和方法进行阈值变化与GP分布状态及其评价剩余寿命、尺度参数值之间的作用关系进行分析，其变化曲线如图1所示。

图1 阈值变化与GP分布尺度、剩余寿命值、形状参数的作用曲线

由图1可知，形状及尺度参数、平均寿命三种指标在阈值为160～250m3/s时处于稳定状态，即在此区间范围内三种指标参数随阈值的变化而不发生明显的改变，并且在该范围内三种指标的置信区间变化幅度较低，因此可认为在此区间取值时POT模型具有较高的确定度。综上所述，POT模型的最佳阈值为190m3/s，各时段阈值的样本极值数量计算结果如表1所示。然后对超阈值样本分别利用三种非参数检验法进行相关假设检验，检验结果见表1。由表1可知，三种双侧检验P在阈值为190m3/s时均高于0.05，即在95%置信区间内不能被原假设拒绝，即POT模型独立同分布的相关要求符合所筛选的超阈值样本结果。

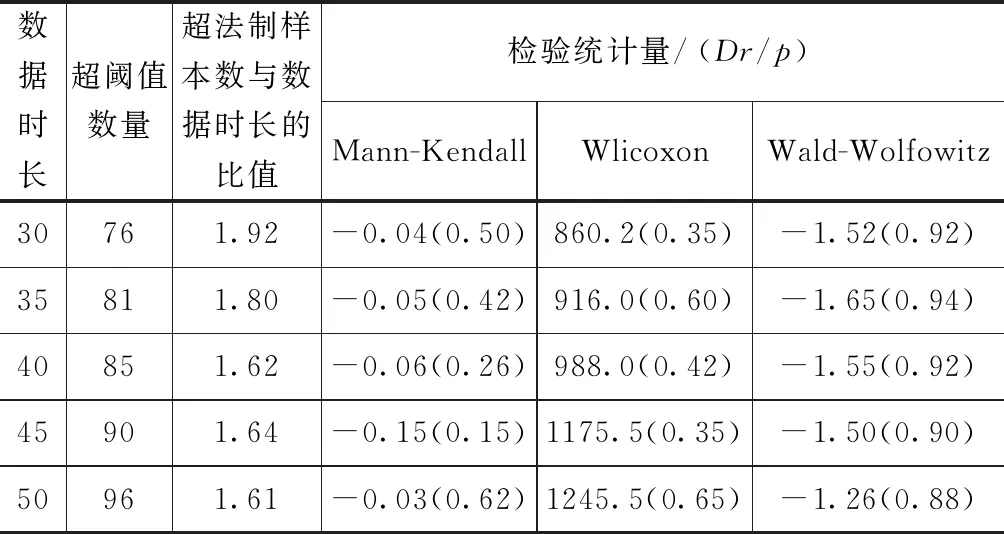
表1 样本独立性检验结果

2.3 重现期及拟合优度检验

对GP分布函数中的各参数利用最大似然法进行估计，因此可确定70%双侧置信区间范围以及不同重现期洪量大小。考虑到5个时段数据GP分布适线图变化趋势的一致性以及文章篇幅原因，本文仅对50a时段数据的GP分布适线图进行分析和讨论。研究表明，理论分布曲线以及样本点经验累积整体沿对角线分布，由此表明GP分布的前提假设基本符合相关参数设定要求，其他时段的变化趋势及验证结果与该时段基本相同。对理论曲线与各时段样本经验点据的吻合程度采用较为常用的统计检验法进行拟合优度检验，检验结果见表2。结果表明：拟合检验P值除了个别时段如30年时段外均高于0.05，依据卡方检验结果和置信水平为95%的K-S检验结果可知样本与理论频率曲线的表现出良好的适线效果。

表2 拟合优度检验结果

2.4 不确定性讨论

为了对计算结果不确定性受时间长度、数据数量多少的作用影响进行研究，本文依据表3有关数据和上述基本过程对5种时段数据上的不同重现期水平值以折现的形式进行描述，其绘制结果如图2所示。

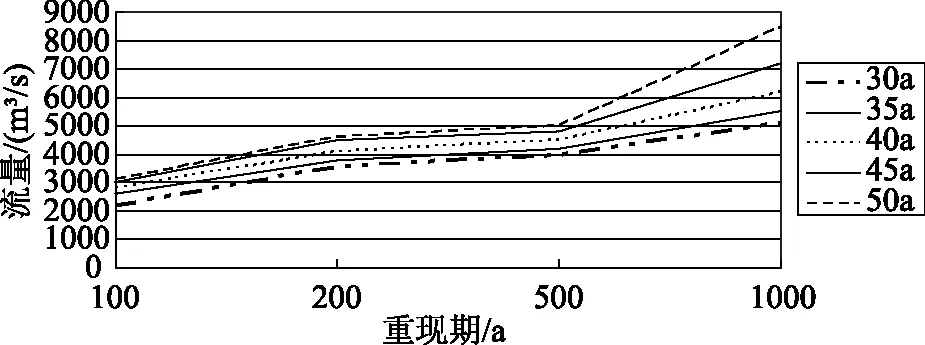
图2 各时段流量资料的重现期水平

由图2可知，辽河流域在1000a、500a、200a和100a日平均洪峰流量重现期水平分别在5100～8500m3/s、4000～5000m3/s、3600～4600m3/s、2200～3100m3/s范围之内。根据纵向变化可知，各重现期计算结果差异范围随所用数据时间程度的增大热表现出增大的趋势，而所用数据的时段长度在同一重现期上的洪水流量大小并未呈现出明显的线性关系。例如各重现期上最大、最小流量值分别可在45年和50年时段上进行求得，重现期计算结果在其他时段样本的处于二者之间。由此表明，重现期计算结果与样本数量的大小以及观测年限长度密切相关，并且样本数量可利用实测数据长度的延长而逐渐增大，环境条件仍然可对新补充的水文条件产生作用影响，对于丰水年份所补充的观测年份可得到离散值偏高的样本，具有代表性的样本可由于长时间枯水实测数据的增大而逐渐不足，虽然采用改进的方法即POT模型仍不能消除此过程的作用影响。研究表明，在实际工程设计中数据资料年限的长短所引起的不确定性可通过设定上侧设计值以及恰当的置信区间进行消除或降低，并因此提高设计成果的准确性与可靠性[12]。

3 结论

本文利用辽河流域出口流量数据资料对GP分布的POT模型进行洪水重现期计算和分析，并对研究区域响应置信区间范围和各重现期流量大小进行研究，理论分布曲线以及经验分布点据分别利用卡方检验、K-S检验进行拟合优度检验，对5种时段流量数据重现期进行计算，得出的主要结论如下：

(1)相对于年最大值取样方法POT模型抽样法可使得数据提高约1～2倍，为符合大样本量对统计分析的有关需求该方法可扩大样本数量。

(2)洪水流量数据拟合优度检验结果显示，GP分布能较好的进行适线并且相对于传统的水文统计分析POT模型能较好的对洪水统计分析。

(3)在实际工程设计中数据资料年限的长短所引起的不确定性可通过设定上侧设计值以及恰当的置信区间进行消除或降低，并因此提高设计成果的准确性与可靠性。