一种强噪声背景下微弱超声信号提取方法研究∗
王大为1)2) 王召巴1)
1)(中北大学信息与通信工程学院,太原 030051)2)(山西师范大学物理与信息工程学院,临汾 041000)(2018年4月24日收到;2018年6月22日收到修改稿)
为解决在强噪声背景下获取超声信号的难题,基于粒子群优化算法和稀疏分解理论提出一种强噪声背景下微弱超声信号提取方法.该方法将降噪问题转换为在无穷大参数集上对函数进行优化的问题,首先以稀疏分解理论和超声信号的结构特点为依据构建了粒子群优化算法运行所需要的目标函数及去噪后信号的重构函数,从而将粒子群优化算法和超声信号降噪联系在一起;然后根据粒子群优化算法可以在连续参数空间寻优的特点建立了用于匹配超声信号的连续超完备字典,并采用改进的自适应粒子群优化算法在该字典中对目标函数进行优化;最后根据对目标函数在字典上的优化结果确定最优原子,并利用最优原子按照重构函数重构出降噪后的超声信号.通过对仿真超声信号和实测超声信号的处理,结果表明本文提出的方法可以有效提取信噪比低至−4 dB的强噪声背景下的微弱超声信号,且和基于自适应阈值的小波方法相比本文方法表现出更好的降噪性能.
1 引 言
无损检测技术在工业中得到了广泛的应用,超声检测是实现无损检测的重要手段[1,2].尤其是近年来非线性超声技术因对被测材料微观结构变化所引起的介质不连续和不均匀更敏感[3−5]而备受关注,如谐波法[6]、混频技术[7]在对材料应力疲劳、微裂纹等表征方面取得了比线性超声更好的效果.制约非线性超声技术应用的重要原因之一是在非线性超声检测中由于通过非线性作用产生的目标超声信号相对线性超声信号幅值较小,同时受到仪器噪声、环境噪声以及被测工件自身非线性的影响,目标超声回波信号中通常包含较大的噪声,给准确提取目标回波信号带来了困难[8].此外,在大型工业基础设施的无损检测中,由于被测材料对超声波的衰减、散射等导致回波信号信噪比无法满足要求,因此增强回波信号的信噪比成为超声无损检测中不可或缺的技术手段之一[9].Sinding等[10]提出一种正则化的超声回波处理方法,相对于经典的带通滤波法不仅提高了处理速度而且可以显著提高降噪后的信噪比;Wu等[11]利用小波变换对获取的超声信号进行降噪处理使降噪后的信噪比提升了6 dB;San和Rodriguez[12]提出了一种基于随机选择移位的小波循环旋转降噪方法,该方法具有平移不变性使得降噪效果优于离散小波变换,但和离散小波变换方法一样在处理含有强噪声的信号时降噪结果会出现失真.
虽然传统的超声信号降噪方法及其改进方法有很多,但它们都是基于傅里叶分析、小波变换的思想.对于接收到的具有一定信噪比的回波信号,可以进一步增强信噪比使之满足后续处理要求,但对于信噪比较低的超声回波信号这些方法难以满足降噪要求.
本文以稀疏分解理论和粒子群优化(particle swarm optimization,PSO)算法为基础,提出一种新的超声信号降噪方法,解决强噪声背景下超声信号的降噪问题.
2 信号稀疏分解及实现算法
稀疏分解是一种在超完备字典上对信号进行分解,并通过优化重构算法求解信号最稀疏表达的信号处理方法,在微弱信号检测方面得到广泛应用[13].但稀疏分解涉及到非确定性多项式难题的求解因而计算复杂,造成其计算量过大的原因有两个:一是稀疏分解中最优匹配原子搜索算法计算复杂;二是超完备字典中原子数目较多.
2.1 信号的稀疏分解理论
信号稀疏分解的基本原理是:对于给定集合D={gi,i=1,2,···,Q},其元素gi是张成整个Hilbert空间H=RN的单位矢量,并有Q≫N,称集合D为超完备原子库,元素gi为其原子.对于空间内任意给定信号f∈H,都可以用D中的m个原子线性表示,即

式中,αi为对应原子的展开系数,且有m≪Q.由于原子库D是超完备的,各原子不是线性无关的,故(1)式的表示方法不惟一.稀疏分解就是从各种可能的分解方法中找出m取值最小的一种表达.
2.2 匹配追踪算法
匹配追踪(matching pursuit)算法[14]是目前信号稀疏分解最常用的方法之一,是强噪声背景下微弱特征提取的有效方法[15],其基本原理为:从超完备原子库D中选取与待分解信号f最为匹配的原子使其满足



(4)式中第k+1次匹配找到的最优原子满足
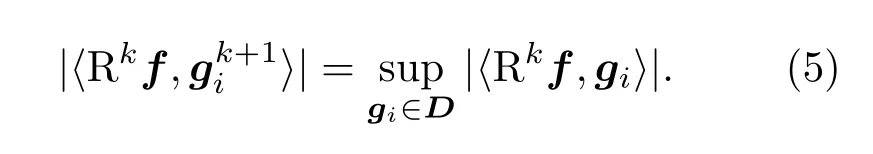
令R0f=f,对信号f进行K次分解后信号可表示为

(6)式表明信号f可分解为K个最优原子的线性组合与第K次分解之后的剩余信号之和.文献[14]研究表明剩余信号的能量会随着K的增大收敛于零.故信号f可稀疏分解为

即信号f可以用超完备原子库中K个最优原子稀疏表示.
2.3 匹配追踪算法的改进
匹配追踪算法是一种遍历所有原子的贪婪算法,因此必须要求用于匹配的原子库是仅包含有限个原子的超完备字典,一般通过离散化字典参数的方法实现超完备字典中原子个数的有限化,例如Gabor字典就是对高斯窗函数g(t)=e−πt2进行伸缩、平移和频率调制得到

然后再对参数γ=(s,u,v,w)离散化:

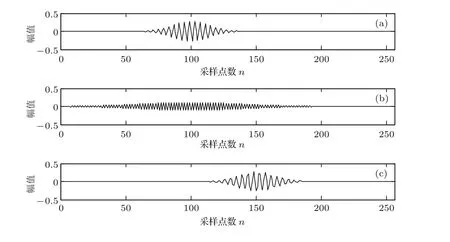
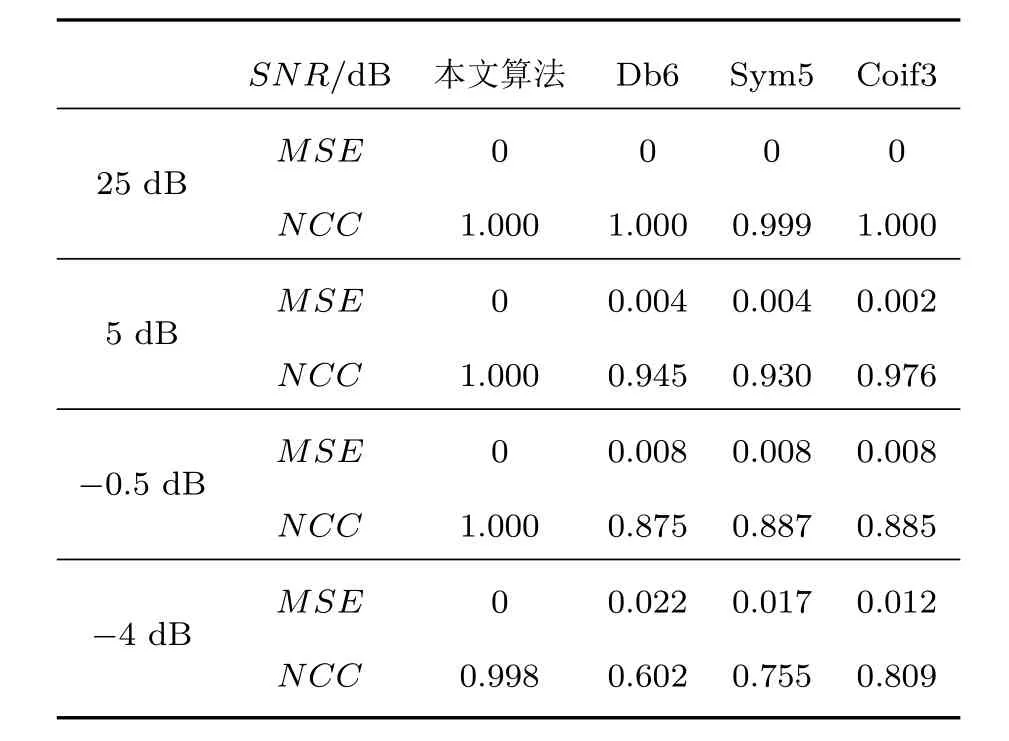
其中,0 这种离散化参数生成可用超完备字典的方法一定程度上会降低超完备字典的冗余性,这与稀疏分解要求超完备字典有尽可能大的冗余性相矛盾. 事实上,利用匹配追踪算法搜索最优匹配原子的稀疏分解中,最优匹配原子搜索需要遍历整个字典,为保证算法完成不得不对Gabor函数的参数进行离散化使其成为原子个数有限的字典.因此作为实现信号稀疏分解手段的匹配追踪算法对字典的要求在本质上和稀疏分解对字典的要求存在不可调和的矛盾.而近年来备受关注的PSO算法可以实现针对连续搜索空间的优化,其在优化支持向量机[16−18]、混沌系统参数估计[19,20]和神经网络训练[21,22]等领域应用十分广泛.根据稀疏分解理论只要能构造合适的目标函数和信号重构算法就可以将PSO算法代替匹配追踪算法直接应用到稀疏分解中,这样不仅可以避免因离散化导致的字典冗余度降低,而且由于优化算法的智能特性还可以加快搜索速度.本文工作的重点之一就是探索构造该目标函数和信号重构算法. PSO算法的数学描述:m个粒子组成一个种群,每个粒子在d维搜索空间中以一定的速度飞行,粒子根据自己搜索到的个体历史最优位置和种群内所有粒子的历史最优位置更新自己的位置. 第i个粒子的位置表示为 第i个粒子的速度表示为 第i个粒子经过的历史最优位置表示为 种群内所有粒子所经过的最优位置表示为 上标t表示进化代数,i∈[1,m].根据如下公式进行速度和位置更新: 其中,w是惯性因子,决定着粒子对当前速度继承的大小;c1是自我学习因子,c2是社会学习因子,在标准粒子群算法中c1,c2取常数,学习因子使粒子具有自我总结和向种群中优秀个体学习的能力,从而向自己的历史最优位置以及种群最优位置靠近;r1,r2为随机因子,服从[0,1]之间的均匀分布. 标准的PSO算法存在“早熟”问题,这是因为(14)和(15)式决定了所有粒子跟随着最优粒子在解空间中搜索并向最优粒子靠近.如果搜索到的最优粒子并非全局最优粒子,且在群体聚集的过程中没有搜索到更优解,那么粒子群算法就会陷入局部最优.惯性因子w值较大时,全局搜索能力较强但局部搜索能力较弱;w值较小时,全局搜索能力较弱但局部搜索能力较强.文献[23]认为在进化初期粒子速度大,快收敛时粒子飞行速度低,基于此提出了利用粒子的平均速度自适应控制w.在本文建立的待寻优参数空间中,粒子速度的每一维度都有特定的物理含义且所用尺度不一样;另外本文是一个最大值优化问题,以评价粒子的适应度函数作为目标函数,在进化初期种群目标函数平均值较小,在进化后期种群目标函数平均值较大.因此受文献[23]启发,结合建立的匹配超声信号超完备字典的参数空间特点,本文提出一种新的方法自适应控制惯性因子w: 式中fit(·)表示粒子的适应度值.因为在进化初期粒子随机分布在参数空间中,各粒子的适应度值差异较大且取值较小,因此δ(t)值较小;随着进化次数增加,粒子逐渐聚合于最优位置,粒子间适应度值差异变小,此时δ(t)值接近于1.因此δ(t)反映了种群的进化深度,其取值范围在(0,1].当w=0.7,c1=c2=2时,在粒子群算法某次进化过程中δ(t)随进化代数的变化规律如图1所示,在进化早期δ(t)发生振荡是因为最优粒子从局部最优跳出,种群向新的全局最优位置聚合导致的. 图1 δ(t)与进化代数的关系Fig.1.Relationship between δ(t)and the number of evolution. 本文以δ(t)自适应地控制惯性因子,其表达式为 c1和c2的大小分别决定着粒子个体历史最优位置、群体最优位置对粒子未来运动速度的影响.在算法进化早期个体历史最优位置相对于全局最优位置有着更重要的作用,因为此时的全局最优位置很可能并非真正的全局最优,故在这个阶段c1的值应取大些,而c2的值要取小些,以粒子自我进化为主从而增强种群的多样性;随着进化过程的进行,全局最优的作用相对凸显出来,因此c1应取小些,而c2应取大些.通过多次对本文构造的目标函数进行重复优化实验和总结,本文采用如下方式自适应控制c1和c2: 式中c0是比例常数.上述学习因子更新方法可以使c1(t),c2(t)根据δ(t)的变化沿着相反的方向自适应变化,它们在平衡全局搜索能力和局部搜索能力方面所起的效果和(19)式是正相关的.本文将w(t),c1(t)和c2(t)分别按(19),(20),(21)式自适应变化的粒子群优化算法称为自适应粒子群优化算法(adaptive particle swarm optimization,APSO).采用APSO算法对本文建立的目标函数进行优化时(c0=1.2),w(t),c1(t)和c2(t)变化趋势如图2所示. 如图2所示,在c点之前粒子的运动方向主要取决于个体历史最优位置,粒子可以充分搜索个体历史最优位置附近的解空间,增强了群体的全局搜索能力;随着进化代数增加,在c点之后粒子的运动方向主要取决于全局最优位置,各粒子向全局最优粒子运动并搜索各自经历的空间,增强了群体局部搜索能力.这样的搜索过程在理论上能使粒子群算法获得更好的优化效果. 图2 自适应因子规律图Fig.2.Change rules of adaptive factors. 为进一步避免算法陷入局部最优,当fitg(t)连续数次停止更新后,用如下更新公式可以有助于解决局部最优问题[24]: 其中xrj表示在参数空间中随机选择的一个粒子. 在脉冲超声检测中,超声脉冲回波信号通常是一个被探头中心频率调制的宽带信号,超声回波的数学模型[25]可建立如下: 式中,A是反射回波幅度,它包含超声波在介质中传播时因衰减而产生的能量损失;α为带宽因子,是一正常数,它决定着超声回波信号的带宽,α越大波形在时间上持续越短,波形越窄,α越小波形在时间上持续越长,波形越宽;τ为回波的到达时间;f0是超声发射脉冲的中心频率;φ是初相位.可以看出,系统接收的超声回波信号是一被探头中心频率f0调制的高斯包络脉冲.(23)式所描述的超声信号本质上是Gabor原子库中的一个原子. 对信号进行稀疏分解的关键是选择一个和信号特性能够匹配的字典.Gabor字典[14]是高斯窗函数经过平移、伸缩和频率调制得到的Gabor窗函数族,其在形式上和超声脉冲表达式相似.根据稀疏分解理论,字典中的原子必须是单位矢量,本文以改进的Gabor函数,即(24)式所张成的希尔伯特空间为超完备字典,称之为匹配超声信号超完备字典,记作D. 式中g(t)=e−πt2是高斯函数;γ=(s,u,v,w)是时频参数,s是尺度因子,控制着高斯脉冲包络的衰减快慢,u是位移因子,控制着高斯脉冲的起始时刻,v是频率因子,控制着高斯脉冲的主频,w是相位因子;λ是归一化因子,其使原子满足单位向量的条件. 图3 不同时频参数的原子 (a)γ1=(20,100,π/2,π/2);(b)γ2=(60,100,π,π);(c)γ3=(20,150,30,40)Fig.3. Atoms with different time frequency parameters:(a) γ1=(20,100,π/2,π/2);(b) γ2=(60,100,π,π);(c)γ3=(20,150,30,40). 由于在本文建立的字典中参数γ=(s,u,v,w)是连续的,因此D中包含的原子个数有无穷多个,词汇量远大于传统的Gabor字典,最优原子必能反映原信号的结构特点.此外,本文方法只需实时产生优化过程中用到的原子,节省了生成字典和读取字典中原子的时间.不同时频参数下本文建立的匹配超声信号超完备字典D中的原子如图3所示. 染噪超声信号的数学模型可表示为 式中,f为含噪超声信号;fs为原始无噪超声信号,fn为噪声信号. 由于无噪超声信号fs是有特定结构的,当构建的超完备字典D能够充分匹配超声信号特征,并在D中对含噪超声信号进行稀疏分解时,fs的结构特性与D中原子的特性是相关的,fs可用D中的原子线性表示;而噪声信号的结构和本文构建的匹配超声信号超完备字典中原子结构是无关的,故噪声无法用D中的原子表示.由于本文构建的字典是一个连续的超完备字典,其中必包含某个原子与超声信号fs匹配,因此降噪问题就是在海量的字典中找出这个原子.两个函数的内积反映了函数的相似性,文献[14]给出了信号与字典相关度的定义,在其基础上本文给出信号f和字典中原子的相关度.其表达式如下: 式中⟨f,gi⟩表示超声脉冲信号f与原子gi的内积,显然,J(f,gi)∈[0,1].当信号f和字典D中任一原子不相关时J的取值为0,当信号f和字典中任一原子完全相同时J取1.J的大小反映了信号f和字典中原子的相关程度. 理论上,噪声与最优匹配原子内积为零而原始无噪信号与最优匹配原子内积为1.故本文把对含噪超声信号的提取转化为对下面目标函数的求解: 经过降噪处理后的信号重构方法为 其中gbest是在匹配超声信号超完备原子库D中找到的最优原子. 基于PSO算法和稀疏分解理论的超声信号提取方法具体步骤如下. 步骤1以原子参数γ=(s,u,v,w)为待寻优参数空间,初始化粒子群,包括种群规模、粒子维数、粒子初始位置、粒子初始速度、粒子位置边界、粒子速度边界、最大进化代数iter等. 步骤2以(26)式为适应度函数,计算每个粒子的适应度值. 步骤3比较粒子当前适应度值和个体历史最优适应度值,如果当前适应度值大于个体历史最优适应度值,则将当前适应度值设置为个体历史最优适应度值;反之不变. 步骤4比较粒子当前适应度值和群体最优适应度值,如果当前适应度值大于群体最优适应度值,则将当前适应度值设置为群体最优适应度值;反之不变. 步骤5根据如下公式更新粒子的速度和位置, 步骤6检查fitg(t)是否连续数次停止更新,若是则执行(22)式然后执行步骤7,否则直接执行步骤7. 步骤7检查是否达到最大迭代次数,若满足则执行步骤8,否则iter=iter+1并转至步骤2. 步骤8记录全局最优原子gbest及Γ. 步骤9根据重构(28)式重构无噪信号,算法结束. 为了验证本文所提方法的有效性,首先对仿真超声信号进行测试与分析,然后再验证对实测超声信号的去噪效果.目前广泛用于评价仿真信号去噪效果的指标有均方误差MSE、波形相似参数NCC及重构信号的信噪比SNR[26,27],其定义如下: 式中s(n)为原始无噪信号,f(n)为降噪后信号. 图4 超声回波仿真信号 (a)理想超声仿真信号;(b)含噪超声仿真信号Fig.4.Simulation of ultrasonic echo signal:(a)Simulation of ideal ultrasonic echo signal;(b)simulation of noisy ultrasonic signal. 理想超声仿真信号及含噪信号如图4所示,其中图4(a)是带宽因子5µs,中心频率1 MHz,延时20µs,初相位0,采样频率10 MHz,采样点数N=512的无噪超声仿真信号波形.超声回波中的干扰主要是高斯白噪声,因此在理想超声仿真信号中加入白噪声模拟含噪超声回波信号.加入方差为0.3个单位的高斯白噪声后的含噪超声回波如图4(b)所示.经计算该信号信噪比为−4 dB. 本文提出了权值自适应变化的PSO算法,待优化参数γ=(s,u,v,w)包含4个维度.s,u分别表示尺度和时延,其在超声信号长度范围内可任意变化;v的物理含义是数字频率,故v∈[0,π];w表示初相位,因此w∈[0,2π].在PSO算法中用粒子位置表示待优化参数γ,具体实验参数设置见表1. 表1 APSO算法参数设置Table 1.Parameters setting of APSO. 为验证本文提出的APSO算法的有效性,分别用本文提出的APSO算法和标准粒子群算法对图4中的含噪信号进行处理,重复实验50次得到的平均重构误差如表2所列. 表2 去噪效果评价指标与实验结果Table 2.Evaluation index of de-noising effect and experimental results. 均方误差MSE反映了原始信号和去噪后的估计信号之间方差的均方,波形相似系数NCC用于评价降噪后信号与理想信号之间的相似程度,重构信号信噪比SNR衡量降噪后信号的凸显程度.均方误差越小、信噪比越大说明去噪效果越好.波形相似系数越接近于1,说明波形越相似.从表2的实验数据中可以看出APSO的三项指标均优于PSO.MSE,NCC,SNR随实验重复次数的变化关系如图5所示. 图5 评价指标波动图Fig.5.Stability of evaluation index. 从图5可以看出,APSO的均方误差MSE、波形相似系数NCC和重构后信噪比SNR不仅平均值优于PSO的对应值,而且方差也小于PSO的对应值.这充分说明与标准粒子群算法相比本文提出的APSO算法显著增强了超声降噪结果的准确性和鲁棒性. 设计本实验旨在验证本文方法可以在强噪声背景下提取超声信号.根据工程中常用超声信号的特点,不失一般性地确定用于本实验的仿真超声信号中心频率f0=1 MHz,带宽因子α=5µs,回波延时τ=20µs,初相位φ=0,采样频率fs=10 MHz,采样点数N=512,将超声信号幅值按最大值归一化为1.在超声信号中依次加入方差从小到大变化的白噪声,用本文算法对含噪超声信号进行降噪处理,对降噪后的重构信号和理想无噪信号进行对比分析,MSE,NCC,重构信号的SNR随所加噪声大小变化规律如图6所示. 图6 评价指标变化图Fig.6.Variation of evaluation index with the increase of noise. 从图6可以看出,当噪声方差小于0.3,即信噪比大于−4 dB时,均方误差MSE为0,波形相似系数NCC为1;在该区间本文方法可以不失真地重构出原始无噪信号,重构信号信噪比SNR在10 dB以上,重构出的无噪超声信号完全满足工程后续处理要求.噪声方差在[0.3,0.55]区间时,随着噪声增大,均方误差MSE增加,重构信噪比SNR减小,波形相似系数NCC出现振荡;该区间的特点是本文方法重构结果不稳定,随噪声增加得到正确结果的概率变小.这主要是因为PSO算法陷入局部最优导致本文算法无法正确匹配到最优原子.噪声方差为0.3(−4 dB)时原始信号、含噪信号、降噪后重构信号的幅值及对应功率谱密度分别如图7所示. 图7中原始信号是中心频率为1 MHz,带宽因子为5µs的超声脉冲信号,在该信号中加入均方差为0.3的高斯白噪声后信号已基本被噪声淹没,此时信噪比为−4 dB.采用本文方法降噪后的重构信号如图7(e)所示,可以看出当信号被噪声淹没时(−4 dB)采用本文方法仍可以不失真地重构原始信号.继续降低信噪比,当噪声方差值为0.5(−8.5 dB)和0.7(−11.2 dB)时原始信号、含噪信号和降噪后重构信号及其对应的功率谱密度的最佳效果分别如图8和图9所示.此时也可以重构出信号,但随噪声增加重构结果稳定性变差且出现失真. 综上,本文算法可以准确重构出信噪比大于−4 dB的含噪超声信号,也可重构出信噪比低于−4 dB的超声信号,但去噪结果的稳定性变差且出现失真. 图7 噪声σ2=0.3时的降噪结果 (a)原始信号;(b)原始信号的功率谱;(c)含噪信号;(d)含噪信号的功率谱;(e)降噪后的信号;(f)降噪后信号的功率谱Fig.7.De-noising results with noise variance σ2=0.3:(a)Original signal;(b)power spectrum of the original signal;(c)signal contaminated by noise;(d)power spectrum of signal contaminated by noise;(e)de-noising result of contaminated signal;(f)power spectrum of the de-noising signal. 图8 噪声σ=0.5时的降噪结果 (a)原始信号;(b)原始信号的功率谱;(c)含噪信号;(d)含噪信号的功率谱;(e)降噪后的信号;(f)降噪后信号的功率谱Fig.8.De-noising results with noise variance σ2=0.5:(a)Original signal;(b)power spectrum of the original signal;(c)signal contaminated by noise;(d)power spectrum of signal contaminated by noise;(e)de-noising result of contaminated signal;(f)power spectrum of the de-noising signal. 图9 噪声σ2=0.7时的降噪结果 (a)原始信号;(b)原始信号的功率谱;(c)含噪信号;(d)含噪信号的功率谱;(e)降噪后的信号;(f)降噪后信号的功率谱Fig.9.De-noising results with noise variance σ2=0.7:(a)Original signal;(b)power spectrum of the original signal;(c)signal contaminated by noise;(d)power spectrum of signal contaminated by noise;(e)de-noising result of contaminated signal;(f)power spectrum of the de-noising signal. 为对比本文算法的降噪能力,选择小波阈值降噪法和本文算法做比较.小波降噪自适应阈值选择基于Stein无偏风险估计原理的rigrsure阈值,小波基选择和超声信号结构有相似点的Db,Sym和Coif小波基,对不同信噪比的信号降噪所得结果如表3所列. 从表3可以看出,当信噪比较大时小波降噪和本文方法都可以取得较好的效果,信噪比较低时本文方法比小波降噪效果更好.当信噪比为−4 dB时,本文方法和小波降噪结果如图10所示. 图10 不同方法降噪对比 (a)原始信号;(b)含噪信号;(c)本文方法降噪后信号;(d)小波降噪后信号Fig.10.Comparison of de-noising by different methods:(a)Original signal;(b)signal contaminated by noise;(c)signal de-noised by our proposed method;(d)signal de-noised by wavelet method. 表3 不同方法降噪结果对比Table 3.Comparison of denoising results obtained by different methods 从图10可以看出,当信噪比降低至−4 dB时,本文方法仍可以对含噪信号取得较好的降噪效果,但用小波降噪方法得到的结果已出现严重失真. 在实验室中用RITEC公司生产的RITEC RAM-5000-SNAP超声检测系统采集了用透射法测试金属构件拉伸疲劳实验的实测超声回波信号进行处理.如图11所示,超声信号采集装置由RAM-SNAP系统、匹配电阻、衰减器、低通滤波器、换能器、示波器以及计算机等组成.实验中设置RAM-SNAP系统激发频率为5 MHz、周期数为7的脉冲信号,经过匹配电阻和低通滤波器传输到换能器上,再由换能器将电信号转换成超声波发射到被测金属试件内部,超声波在被测试件内部传播到达试件表面后发生透射,透射的超声波被换能器接收后再转换为电信号,最后接收到的信号在示波器上显示.本实验的目的是采集实测含噪超声信号,通过采用本文方法对实测含噪超声信号进行降噪处理,从而验证本文方法可以有效地提取强噪声中的实测超声信号. 图11 超声信号采集装置Fig.11.Ultrasonic signal acquisition device. 由于和工程实际相比实验室环境中的噪声很小,本文把无激励时测试到的系统噪声放大后叠加到信号中.实测超声信号和测试系统噪声如图12所示. 采用本文方法和小波方法对实测强噪声背景下含噪超声信号进行降噪处理,降噪前后信号时域和频域对比如图13所示. 从图13(a)可以看出,由于在实验室环境下测试系统中噪声较小,实测超声信号中包含少量噪声.为比较本文算法和小波方法的降噪性能,将测试系统噪声放大,并与超声信号叠加,所得到的含噪信号如图13(c)所示.通过对比图中不同方法的降噪结果可以看出,本文方法对实测超声信号的降噪结果无论在时域还是频域都优于小波阈值降噪. 综上所述,本文方法可以准确提取淹没在强噪声(SNR>−4 dB)中的实测超声信号,而且降噪效果好于基于自适应阈值的小波降噪方法.对于SNR<−4 dB的强噪声本文方法也可以实现降噪,但算法稳定性下降. 图12 (a)实测超声信号;(b)系统噪声Fig.12.(a)Measured ultrasonic signal;(b)measured system noise. 图13 实测信号降噪前后时-频对比 (a)实测超声信号;(b)实测超声信号功率谱;(c)叠加噪声的实测超信号;(d)叠加噪声的实测超声信号功率谱;(e)本文方法降噪后结果;(f)本文方法降噪后信号的功率谱;(g)小波方法降噪后的结果;(h)小波方法降噪后信号的功率谱Fig.13.Comparison of measured signals before and after denoising:(a)Measured ultrasonic signal;(b)power spectrum of the measured ultrasonic signal;(c)measured ultrasonic signals contaminated by noise;(d)power spectrum of signal contaminated by noise;(e)signal de-noised by our proposed method;(f)power spectrum of the signal de-noised by our proposed method;(g)signal de-noised by wavelet method;(h)power spectrum of the signal de-noised by wavelet method. 本文基于PSO算法和稀疏分解理论提出了APSO-SD超声信号提取算法,并通过仿真和实测验证了本文算法可以有效提取强噪声中的微弱超声信号. 1)将超声信号降噪问题转化为对约束函数的优化问题.随着深度学习的发展和优化算法性能不断提升,相信在不久的将来这种信号处理方法将会成为继傅里叶分析、小波变换之后的又一种重要的信号处理手段. 2)基于超声信号的结构特性建立了匹配超声信号超完备字典D,利用超声信号与字典中原子必然相关而噪声与字典中原子无关这一事实构造了目标函数和信号重构函数,将超声信号降噪和智能优化算法联系在一起. 3)对粒子群算法做了改进,提出了一种基于粒子适应度值自适应变化的PSO算法,增强了本文算法的鲁棒性. 同时还存在一些问题,例如在信噪比低于−4 dB时本文算法的稳定性变差,这是由于APSO算法陷入局部最优导致的.如果能够开发出性能更加优良的优化算法,利用本文降噪思想将可以对更低信噪比的超声信号取得更好的降噪效果,这也是我们下一步研究的重点.3 PSO算法介绍和改进
3.1 标准PSO算法






3.2 PSO算法的改进





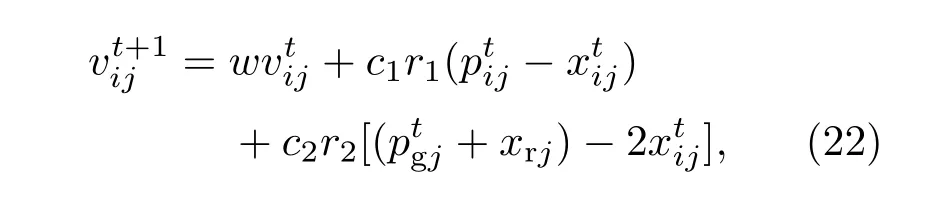
4 本文算法
4.1 超声信号模型
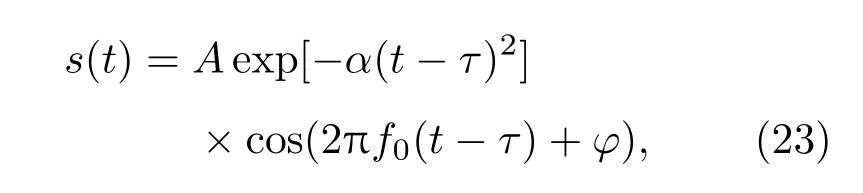
4.2 建立匹配字典

4.3 构建目标函数




4.4 算法流程

5 仿真验证与结果分析

5.1 超声信号仿真

5.2 APSO参数设置与实验



5.3 去噪性能分析




5.4 本文方法和小波降噪对比

6 实测信号验证



7 结 论

