非线性系统相轨迹教学仿真平台设计

张 婧，盖文东，高宏岩，卢 晓

(山东科技大学 电气与自动化工程学院,山东 青岛 266590)

几乎所有的实际系统都具有非线性特性。非线性程度较弱且运行在平衡点附近较小范围内的系统,可采用小偏差法将其线性化作为线性模型处理；而非线性特性较明显或非线性因素无法忽略的系统,只能采用非线性系统理论进行研究[1-2]。有时,在解决工程问题时,人为地引入非线性部件可改善系统的性能或简化系统的结构。因此研究非线性系统的分析和设计方法是非常必要的。

目前工程上常用相平面法和描述函数法分析和研究非线性系统。相对描述函数法,相平面法不仅可以判断系统的稳定性和自激振荡,还可以讨论系统在不同初始条件以及在不同输入信号作用下的运动状态,可全面形象地获得系统运动的全部信息[3]。

针对非线性系统的分析和设计问题,相平面法在实际工程中应用范围较广,如可采用相平面法分析飞行控制、车辆行驶、电力系统暂态响应等非线性系统的稳定性及电网中单相接地故障、发电机组故障的诊断[4-8],也可采用相平面法设计飞行器舵机负载模拟器和飞行器的控制器[9-10],因此掌握如何绘制相轨迹及利用相平面法分析系统也是非常必要的。但是由于相平面法是一种图解法,使用时需要绘制大量曲线。在相关内容的教学过程中,教师在黑板上绘制曲线的准确度难以保证,导致系统的性能也难以体现。教学实验着重采用相平面法分析含有典型非线性环节的非线性系统,但在实验过程中经常会因为元件参数不稳定,实验值与理论值不太吻合,导致学生产生错误的理解[11]；并且,由于实验箱分立元件众多,元件组成的传递函数接线较复杂,导致学生不知如何调整实验参数。为了解决这些问题,期望能够找到一种可以通过交互界面设置或修改系统参数,从而直观准确地绘制非线性系统相轨迹的方法。

一阶或二阶非线性系统相轨迹的绘制较为简单,高阶系统相轨迹的绘制则较为困难。文献[12-13]阐述了高阶系统可采用δ法或等倾线法绘制相轨迹,但这两种方法比较复杂；文献[14]借助MATLAB文本语言绘制高阶非线性系统的相轨迹,这种方法需要根据非线性环节的分界线将线性环节的传递函数写成分区线性微分方程再利用ode函数求解,因此也较为复杂；而文献[15]则借助Simulink仿真工具高阶非线性系统仿真模型绘制相轨迹,但当系统参数及初始条件发生变化时,操作较为复杂,仿真结果也不直观。

基于上述考虑,本文将MATLAB中的Simulink仿真工具箱和GUI引入到教学中,设计开发了非线性系统相轨迹的教学仿真平台。首先通过Simulink构建非线性系统的仿真模型；然后通过GUI交互界面调取仿真模型,并设置或修改系统输入信号、开环增益、初始条件等参数；最后直观、准确地绘制非线性系统的相轨迹,分析非线性系统的性能。仿真平台交互性好,操作简单,既能丰富教学手段,又有助于学生加深对相平面的理解,可以激发学生的学习兴趣,培养学生的研究能力和创新能力。

1 教学仿真平台的总体方案

Simulink仿真工具箱以框图形式描述系统的模型,进行动态系统建模、仿真和综合分析,其框图化的设计方式简化了编程；图形用户界面(GUI)可以实现人与计算机信息交换的功能,操作简单,形象直观。将Simulink和GUI结合,利用GUI的友好交互界面,在界面中设置或修改Simulink模型参数,并且实时显示期望的仿真结果,这将会对精确绘制非线性系统的相轨迹提供方便,同时有利于提高教学效果。

基于GUI设计的非线性系统相轨迹教学仿真平台上包括多个组件,需编写每个组件的回调函数,以便完成用户与GUI的交互功能。在GUI界面上输入系统的相应模型参数,回调函数接收这些参数并将参数值传递到Simulink模型中,根据输入的参数值设置相应模块的参数进行仿真；然后将仿真结果传到Workspace,得出系统响应的输出数据；最后利用输出数据在GUI界面上绘制相轨迹。教学仿真平台通过交互界面实现调取仿真模型、设置或修改系统各项参数、绘制非线性系统的相轨迹等各项功能,其总体设计方案如图1所示。

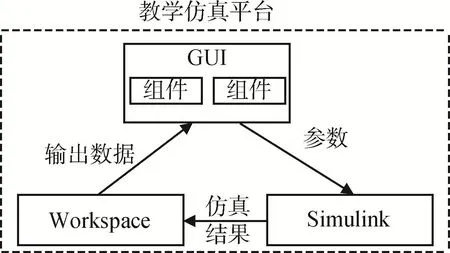
图1 教学仿真平台总体设计方案

2 非线性系统相轨迹教学仿真平台的构建

对于用非线性微分方程描述的非线性系统,可调用MATLAB的ode及plot函数,先求解系统微分方程高阶数值,再在相平面上绘制相轨迹；而对于某些由多个不同线性微分方程描述的分区非线性系统,可在不同分区内绘制相轨迹再分析。本文主要讨论含有典型非线性环节的分区非线性系统,其结构图如图2所示。

图2 含有典型非线性环节的非线性系统结构图

下面将以一示例来详细介绍非线性系统相轨迹教学仿真平台的构建。示例为:

非线性系统结构图如图3所示,h＝1,a＝1,系统的初始条件为[c(0),(0),(0)]＝[0.6,1,0.7],要求在相平面c-上绘制系统的相轨迹。

图3 非线性系统的结构图

2.1 基于Simulink的仿真模型构建

将示例中线性环节的传递函数写为可观标准型的状态空间表达式:

之所以将高阶线性环节部分写成可观标准型,是因为可观标准型的特点是线性环节的输出c(t)恰为最后一个状态变量xn,即状态变量图中最后一个积分器的输出就是线性环节的输出c(t),其输入为线性环节输出的一阶导数(t)。若已知系统输出的初始条件,或要求根据相平面法分析高阶非线性系统的运动特性,即在相平面c-上绘制系统的相轨迹,相较可控标准型,可观标准型的表示方法更为简便。

由于构建的仿真模型是以状态变量图表示,所以需要将输出量初始值变为状态变量初始值。由已知条件[c(0),(0),(0)]＝[0.6,1,0.7]及式(1),得:

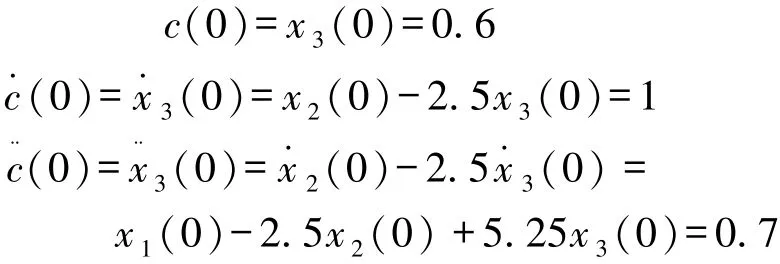
求得状态变量初始值[x1(0),x2(0),x3(0)]＝[3.8,2.5,0.6]。

在Simulink中将图3所示的线性环节以状态变量图表示,再结合非线性环节构造仿真模型如图4所示,命名为“honl”。其中,点划线框内为系统的输入信号,由于输入信号一般为无信号输入、阶跃信号、斜坡信号或两种输入信号之和,故将其幅值和斜率都预先设置为0,在仿真平台上可修改其幅值参数。虚线框内为构建的非线性系统模型,为便于直观显示,将状态变量的初始值都预设为0且设置在积分器外面,在仿真平台上可设置或修改初始值；线性环节的开环增益K也可在仿真平台上修改,当K取不同值时,相轨迹和系统动态响应形式皆不同；线性环节的状态变量关系,即Gain1,Gain2,Gain3的值也可以在仿真平台上修改,即改变系统的模型参数,由题意可知,仿真平台上a、b、d的值分别为2.5,1和0。为了能够在仿真平台上绘制相轨迹,在仿真模型中将示波器Scope和Scope1的数值保存到MATLAB的工作区间内,以便仿真平台调用数据。

图4 基于Simulink的非线性系统的仿真模型

2.2 基于GUI的教学仿真平台界面构建

基于GUI的非线性系统相轨迹仿真教学平台界面如图5所示。

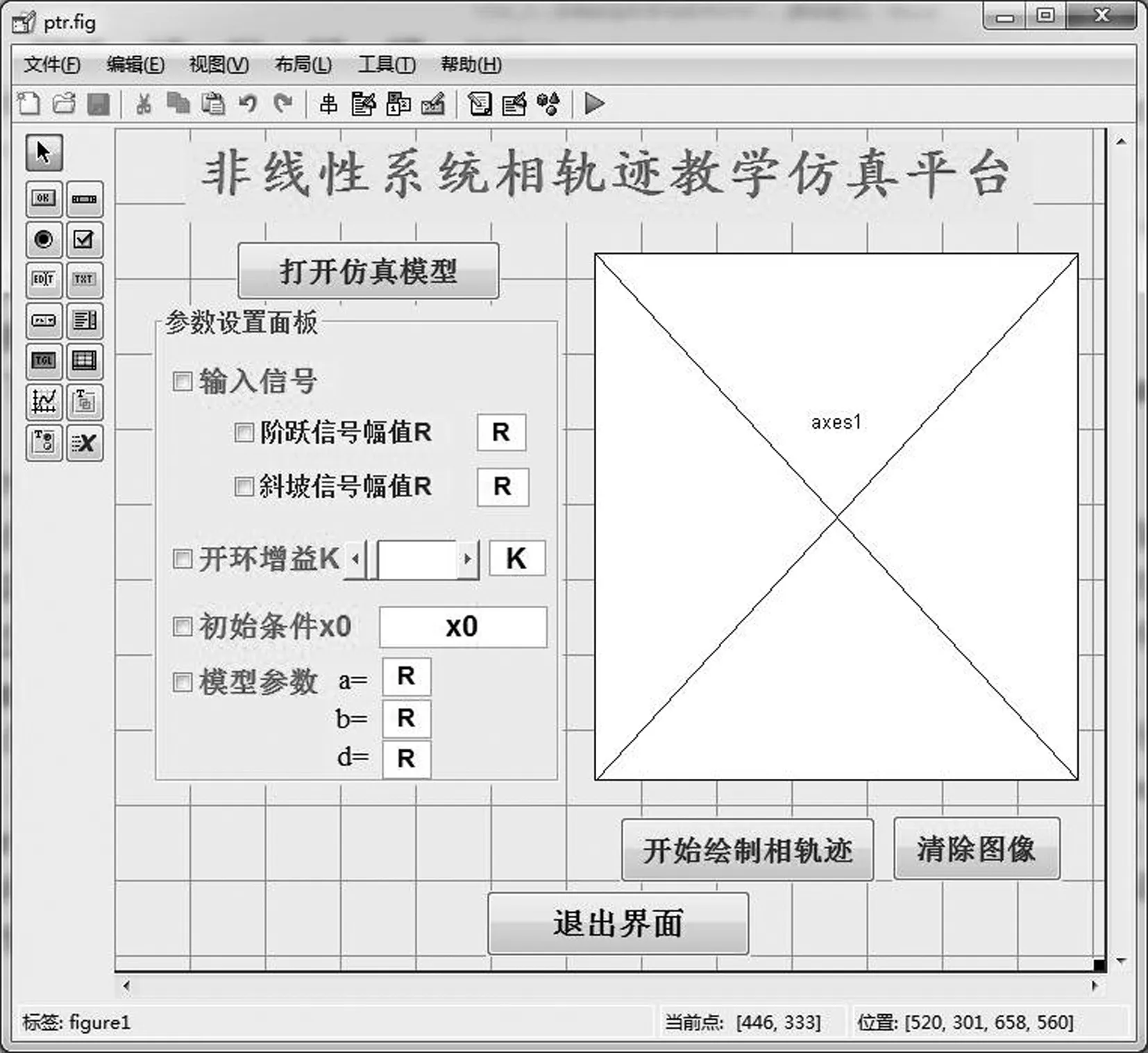
图5 基于GUI的非线性系统相轨迹教学仿真平台界面

保存界面同时生成 “ptr.jpg” 和 “ptr.m” 两个文件。前者每个组件都对应其句柄图形,后者是根据编写的组件回调函数实现预定的交互功能[16]。下面主要介绍GUI界面实现交互功能的方法。

在运行GUI界面时,点击 “打开仿真模型”按钮,需实现调取2.1节构建好的仿真模型。其回调函数程序为

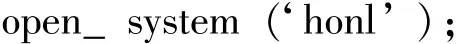
点击 “开始绘制相轨迹”按钮,在axes1坐标轴上绘制相应的相轨迹。需要先将Simulink中Scope和Scope1的数据 “c” 和 “dotc” 存到Workspace中,再根据存储的数据绘制相轨迹,所以需要定义全局变量,其回调函数如下:

global c

globaldotc

handles＝guidata(gcf)；

axes(handles.axes1)；

sim(‘honl’)；

plot(c.signals.values,dotc.signals.values)

hold on

grid on

选中 “开环增益”的复选框。为了体现参数逐渐变化对相轨迹的影响,用滑动条来实现参数的平滑调整。在 “Slider”的属性中可以修改其最小值和最大值,点击或拖动 “Slider”,就可以在“EditText”中显示实时的开环增益。其回调函数为:

set(handles.edit3,'string',num2str(get(handles.slider1, ‘Value’)))

利用MATLAB提供的get()函数获取开环增益K的值,再用 set＿param()函数设置仿真模型“Gain”的数值K,其回调函数为:

s＝get(handles.checkbox4, ‘value’)；

if(s＝＝1)

b＝char(get(handles.edit3,'string'))；

set＿ param(‘honl/Gain', ‘Gain',b)；

end

GUI界面上其他组件的回调函数程序的编写类似,不再赘述。这样就可以在GUI界面上随时设置或修改参数,不需要再进入Simulink环境。点击“开始绘制相轨迹”按钮就可绘制各种条件下的非线性系统的相轨迹,实现期望的非线性系统相轨迹教学仿真平台的交互功能。

3 非线性系统相轨迹教学仿真平台的应用

在仿真平台界面上设置或修改参数,并绘制相轨迹,得到的Simulink仿真模型如图6所示,仿真平台界面如图7所示。由图7可知,不论开环增益K取何值,相轨迹都从初始条件(0.6,1)出发,以不同形式运动。当K＝1时,相轨迹以螺旋线的方式最终趋于稳定,且稳定在坐标原点；当K＝2.54时,相轨迹最终趋于极限环,系统输出呈现自激振荡,振幅约为1.1。根据上述分析可知,令系统出现自激振荡的临界值K＜2.74,经实验得到临界值为2.5。

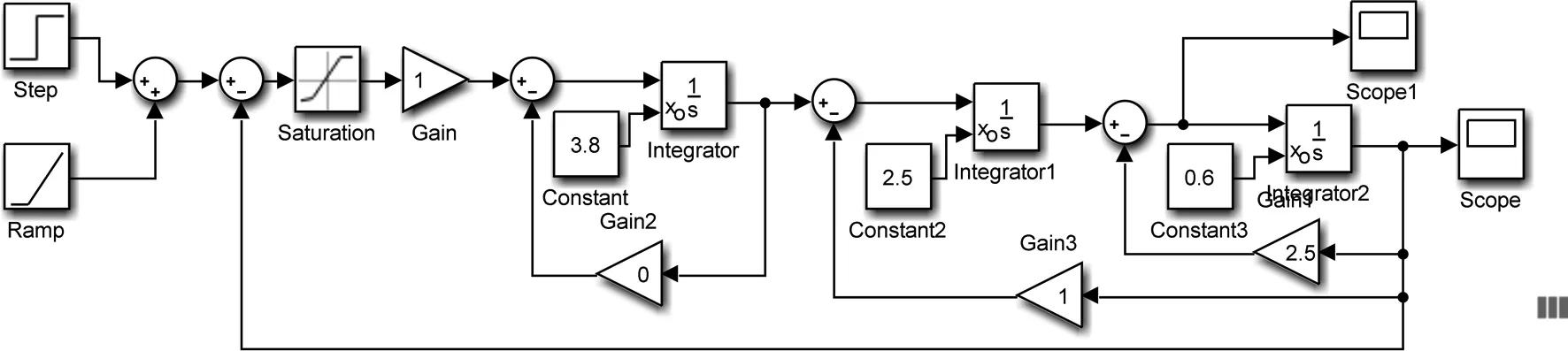
图6 根据题意设置Simulink仿真模型 (K＝1)

在仿真平台上还可以分析当初始条件不变输入信号发生变化时的相轨迹,界面如图8所示；分析当输入信号不变初始条件变化时的相轨迹,界面如图9所示。由图8和图9可知,相轨迹不仅与初始条件有关,也和输入信号的形式与幅值等有关。

图7 在仿真平台上设置参数并绘制的相轨迹

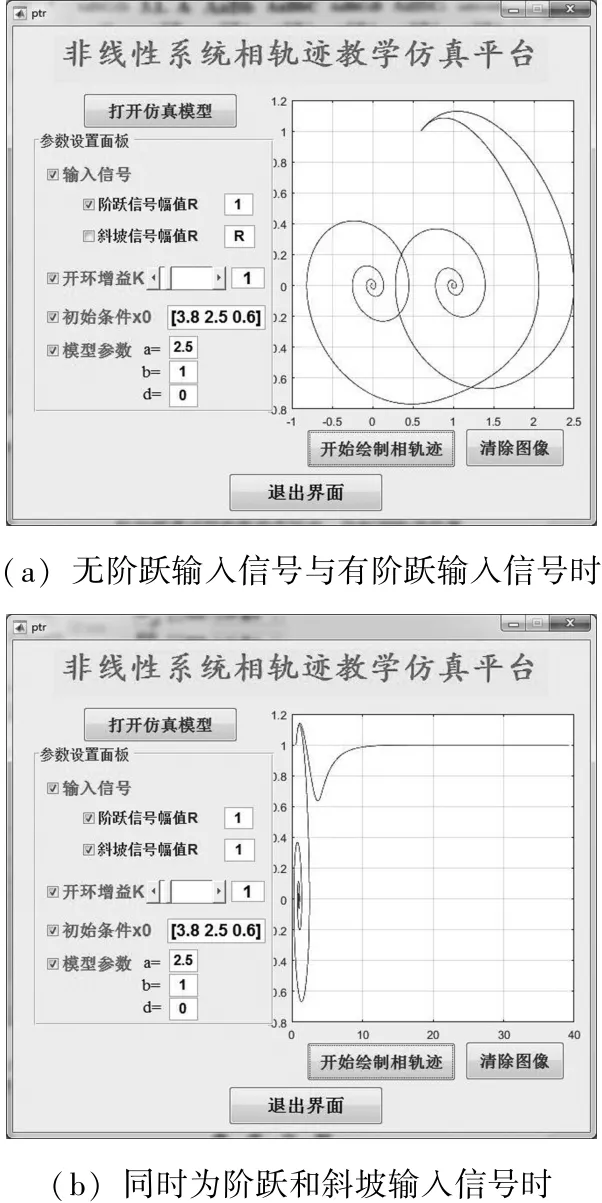
图8 初始条件不变输入发生变化时绘制的相轨迹

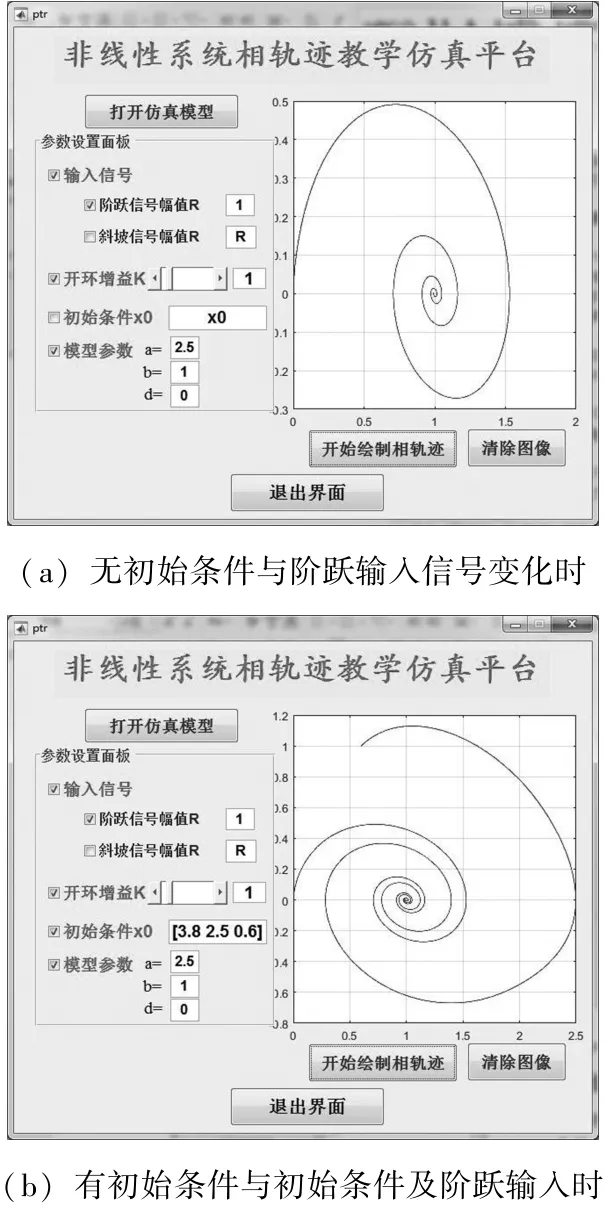
图9 输入信号不变初始条件变化时绘制的相轨迹

除此之外,在教学仿真平台上修改模型参数,即可改变线性环节的数学模型,可用同样方式绘制新非线性系统的相轨迹并分析其性能；还可以在Simulink仿真模型中修改非线性环节的数值及特性,如将饱和特性换为继电特性或死区特性等,甚至可以是多种非线性特性的组合,这些问题可以作为课后思考题供学生学习和思考,本文不再赘述。

由非线性系统相轨迹教学仿真平台可以很直观地看到系统在不同初始条件以及在不同输入信号下绘制的相轨迹是不同的,而根据精确绘制的相轨迹不仅可以判断非线性系统的稳定性,还可以判断系统是否产生自激振荡及产生自激振荡的条件和振荡幅值,甚至可以稍微修改aexs1回调程序,进一步得到系统的性能指标。

4 结束语

针对授课过程和教学实验中,绘制相轨迹的复杂性、不准确性和不直观性的问题,本文将MATLAB中的Simulink仿真工具箱和GUI引入到教学中,设计开发了非线性系统相轨迹的教学仿真平台。该教学仿真平台可根据需要构建非线性系统的仿真模型,可交互性地设置或修改系统参数,绘制相应的相轨迹。近几年来的教学实践表明仿真平台交互性好,操作简单,既能丰富教学手段,又可以帮助学生加深对相平面的理解和学习,激发学生的学习兴趣,培养学生的研究能力和创新能力,改善教学效果,提高教学质量。