弗兰克-赫兹实验探究
吴 静,陈艺超,严一民,姚列明
(1.电子科技大学 物理学院,四川 成都 610054)
1913年波尔提出了关于原子结构的一种理论——玻尔理论,这是在卢瑟福原子模型基础上加上普朗克的量子概念后建立的。具体来说,玻尔理论包括:1)原子能量的量子化假设,原子只能处于一系列不连续的能量状态中,在这些状态中的原子是稳定的,电子虽然做加速运动,但并不向外辐射能量;2)原子能级的跃迁假设,原子从一个定态跃迁到另一个定态时,原子辐射一定频率的光子,光子的能量由这两种定态的能量差决定;3)原子中电子运动轨道量子化假设,原子的不同能量状态对应于电子的不同运行轨道。由于原子的能量状态是不连续的,因此电子运动的轨道也可能是不连续的,即电子不能在任意半径的轨道上运动[1-2]。为了证明原子内部量子化能级的存在,1914年,弗兰克(James Franck)和赫兹(Gustar Hertz)在研究中分别发现电子与原子发生非弹性碰撞时能量的转移是量子化的。他们的精确测定表明,电子与汞原子碰撞时,电子损失的能量严格地保持4.9 eV,即汞原子只接收4.9 eV的能量[3]。
改变原子能级的方法有许多种,通常在两种情况下可让原子状态改变:1)当原子吸收或发射电磁波时;2)用其他粒子碰撞原子而交换能量时。用电子轰击原子实现能量交换最方便,因为电子的能量可通过改变加速电场V来控制。弗兰克-赫兹实验就是用这种方法证明了原子能级的存在。基于此,关于原子内部结构以及慢电子轰击原子的实验规律得以实现,通过测量电子和原子碰撞时交换某一定值的能量,直接证明了原子内部量子化能级的存在,同时也证明了原子发生跃迁时吸收和发射的能量是完全确定的、不连续的,给波尔的原子理论提供了直接的而且是独立于光谱研究方法的实验证据。在后续的发展过程中,弗兰克-赫兹实验采取了许多优化措施,例如经常采用将管内抽取至高真空后,冲入各种高纯度气态物质,如惰性气体-氩气或其他元素气体来进行实验。本文实验中,采用电子科技大学的智能充氩弗兰克-赫兹管测量程序,可以设置时间、手动或者自动测量方式,而不是采用示波器测量,这基本消除了实验中由于时间演化所带来的数据不准确的误差。采用内部热阴极电子进行加热的方式,用慢电子轰击氩原子。
1 实验装置
本文弗兰克-赫兹实验所采用的真空弗兰克-赫兹管,管内充满氩气。在弗兰克-赫兹管中所使用的弗兰克-赫兹仪的参数为:电源电压为220 V,50 Hz,最大电源电流为0.5 A。灯丝电压范围为0~6.3 V,±0.063 V;第一栅极电压范围为0~5 V,±0.05 V%;第二栅极电压范围为0~100 V,±1 V;拒斥电压范围为0~12 V, ±0.12 V;电流(IA)1μA~1 mA。
2 结果讨论
如图1(a)~1(d)所示,分别给出了在加速电压为1.6 V,反向拒斥电压为8.0 V,温度26℃时,灯丝电压范围为2.3~2.6 V时,弗兰克赫兹管伏安特性曲线图。分别对波谷和波峰的电压值进行标定,相应的电压间隔就是氩的第一激发电势。采取线性拟合的方法(逐差法,最小二乘法线性拟合),对实验结果进行求解。从拟合结果可以得到,当阴极电压逐渐增加的过程中,所计算的结果误差越来越小(6.95%,6.59%,6.43%,6.43%);而采用波谷计算的结果误差(4.29%)要比波峰计算的结果误差(6.29%)要小。热阴极电压增加,导致电子能量增加,这样发生碰撞的概率就会增加,导致电子与原子碰撞能量交换发生的概率增加,有利于达到更为平衡的条件,因此对于准确结果的获得可能更为有利。
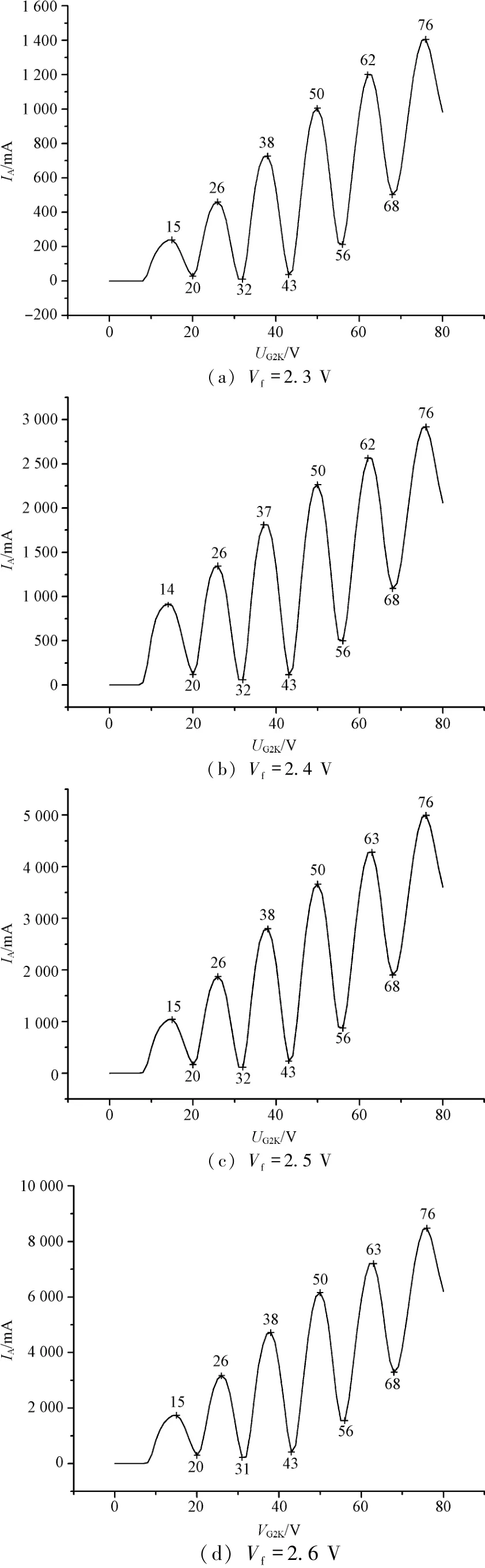
图1 加速电压为1.6 V,反向拒斥电压为8.0 V,温度为26℃时,灯丝电压V f的弗兰克赫兹管伏安特性曲线
在文献[4]中给出了相关的解释:弗兰克-赫兹管中所采用的材料不尽相同,因此会产生接触电势差。接触电势差的大小应该与两种材料的逸出功有关,可以通过一个方程进行修正:

式中,P1为氩原子的第一激发电势[4-7],P2为接触电势差等因素引起的电势差。由于空间电荷对加速电压的影响,峰位序数n和对应加速电压具有线性关系。
本文采用最小二乘法对上述测得的实验数据进行处理。从线性拟合曲线可以计算出氩原子的第一激发电势。从结果可以看到,灯丝电压的变化对极板电流的影响非常大,在其他条件相同的情况下,灯丝电压Vf越高,极板电流IA越大。灯丝电压的增加,实际上是功率增加。在其他参数不变的情况下,灯丝温度增加,单位时间内从热阴极K到达阳极极板A上的总电子数目增加,从而导致极板间电流IA增加。灯丝电压不能过高或过低。因为灯丝电压的高低,确定了阴极的工作温度,按照热电子发射的规律,影响阴极热电子的发射能力。灯丝电位低,阴极发射电子的能力减小,使得在碰撞区与氩原子相碰撞的电子减少,从而使板极A所检测到的电流减小,伏安特性曲线的分辨率下降给测量带来困难。从拟合的方式来看,由于峰值和谷值数据点较少,并不能很好地说明两种方法哪种拟合好,而最小二乘法依赖大量数据的计算,可得到较好的线性相关度。由于实验电压限制(击穿),因此只有有限的拟合数据点。
在本文实验中,所测量得到的氩的第一激发电势12.0 eV左右,与理论值13.06 eV相差有5%左右的误差。由于在第一激发态和基态之间还存在着两个亚稳态[4](11.55 eV和11.72 eV),氩原子外层电子在这两个亚稳态的停留时间为10-3s,比第一激发态的停留时间(10-8s)要长许多。因此从能级理论角度上讲,所测量的结果应该要进行修正,考虑两个亚原子能级。当慢电子从热阴极产生,经过加速与氩原子发生碰撞,有可能存在到这两个寿命更长的氩原子能级上。氩原子不仅以一定的概率跃迁到了13.06 eV这个理论值的能级上,还以一定的比率跃迁到了能量差值为11.55 eV和11.72 eV这两个亚稳态上。该实验测量得到的激发电位本质上应为第一激发电势和两个亚稳态激发电位的一定概率比,与其内部原子的结构有千丝万缕的联系[1,8-9]。由于电子和氩原子碰撞能量交换是复杂的过程,能量交换与电子能量分布、氩原子密度分布、板间间距、弗兰克-赫兹管温度等都关系紧密。由于电子和氩原子碰撞发生能量交换的程度与电子能量分布及对应电子的激发概率的乘积有关,如果提高实验精度,可以测量得到峰值电压间距和谷值电压间距都在变化,而不是一个恒定值,会出现峰值和谷值扰动,这跟管温及板间间距都相关。不仅如此,在测量结果的修正上,应该还要考虑接触电势差。如式(1)所示,P2应该为接触电势差,但是在测量的结果上接触电势差不仅仅跟材料的逸出功相关,还与温度、电压等参数相关,因此不能仅仅像文献[4]中,简单地扣除接触电势差,而应该给出接触电势差动态的变化,这个也是一个较为明显的实验误差来源,应该提醒学生注意。
3 结束语
通过测量与计算充氩弗兰克-赫兹管在特定的条件,不同的灯丝电压条件下,伏安特性曲线的规律,利用逐差法和最小二乘法线性拟合了曲线峰值和谷值的线性关系,计算得到了氩原子的第一激发电势,进一步验证了非弹性碰撞的近似模型。由实验结果发现:根据近似理论模型假设计算所得的氩原子第一激发能与理论值较为相近,但是,氩原子实验结果的误差似乎较大。由此说明,利用上述实验方法只能得到所测气体的第一激发能的不太精确的数值,原因是在第一激发态左右,会有两个亚稳态(11.55 eV和11.72 eV)。氩原子对电子能量的吸收应该是一个比较复杂的过程,根据量子力学能级理论,电子的分布会出现一定的概率,假设电子分布满足玻尔兹曼分布,但是因为在低能和高能部分的分布不同,因此不能简单地根据加速电压确定电子和氩原子的实际碰撞,而应该为13.3 eV、11.55 eV和11.72 eV共同作用的结果,观察到的氩原子第一激发能是这三条谱线共同作用的结果。由于初始时刻加速电压较小,能量较低的电子数目较多,因此碰撞交换能量的概率小,但是随着加速电压的增加,电子能量分布朝着高能部分移动,因此,电子与三个能级的氩原子交换能量的概率增加,总的间距依次在增加,这在许多实验中有所观察[8-10]。总之,本文实验测量得到的激发电位本质上应为第一激发电势和两个亚稳态激发电位的一定概率比,接触电势差的存在。另外,由于弗兰克-赫兹管的结构和实验参数会有一些不尽相同,需要找到最适合的点去测量,才能保证实验结果有较高的准确性。由于本文中所选用的是氩原子和电子相互碰撞,而氩原子的第一激发电势为13.1 V,因此所得到的峰值比较少,用最小二乘法得到的计算结果精度较逐差法低,随着数据量的增加,最小二乘法要更为精确。尽管如此,在弗兰克-赫兹实验中,宏观电流IA的变化趋势体现着内部电子与原子相互碰撞的结果,在理论以及宏观的物理现象中揭示了原子内部的信息,弗兰克-赫兹实验架起了微观原子结构和宏观世界之间的桥梁。弗兰克-赫兹实验在测量中计算的结果跟理论值有一定偏差,尝试从材料接触电势差和能级亚稳态出发,去解释微观的物理模型,增强学生的感性认知。

