基于频域匹配滤波的音频信号分析与识别

赵凌览，李晓峰

(电子科技大学 信息与通信工程学院,四川 成都 611731)

乐音音符识别和自动乐谱编制研究的基本目的在于使计算机听懂乐器的演奏并自动谱曲,在音乐创作中有很重要的实用价值。目前已有相当一部分的相关文献报道[1-2],其通过对检测到的音符进行频域分析,使用小波变换或者滤波的方式将音符的有效频率集中在基频频率附近,除去泛音干扰分量,而后通过识别基频频率的方法实现单个音符的识别。

本文提出一种基于频域匹配滤波进行音阶识别的方法。在识别基频频率的基础上对其泛音分量也进行匹配,在一定程度上提高了识别的可靠性与准确度；此外,对于音频信号的每一个频谱峰值,利用Goertzel算法计算出对应的单一谱线进行表示,提高了运算和识别的效率,同时又不失一般性。

最后,本文以钢琴标准音频文件、手机钢琴演奏软件以及真实的钢琴演奏录音等多种音源的部分音符为例进行了测试,测试结果表明:该方法具有较高的识别准确度和良好的抗噪性能。

1 乐音的基本特性

1.1 乐音的音乐特性

一段连续的乐音是由一系列不同音高的音符按照时间顺序发声组成的,音符的频域通常由两部分组成:基音频率和泛音频率。基音频率决定乐音的音高；而泛音频率决定音色[3]。泛音由基音频率的各整数倍频率构成,实测发现泛音各次谐波的幅度和基音频率对应的幅度之比基本是固定不变的。所以,利用音符的特定频谱特性,就能很好地实现对乐音信号的识别。本文的音频识别算法如图1所示。

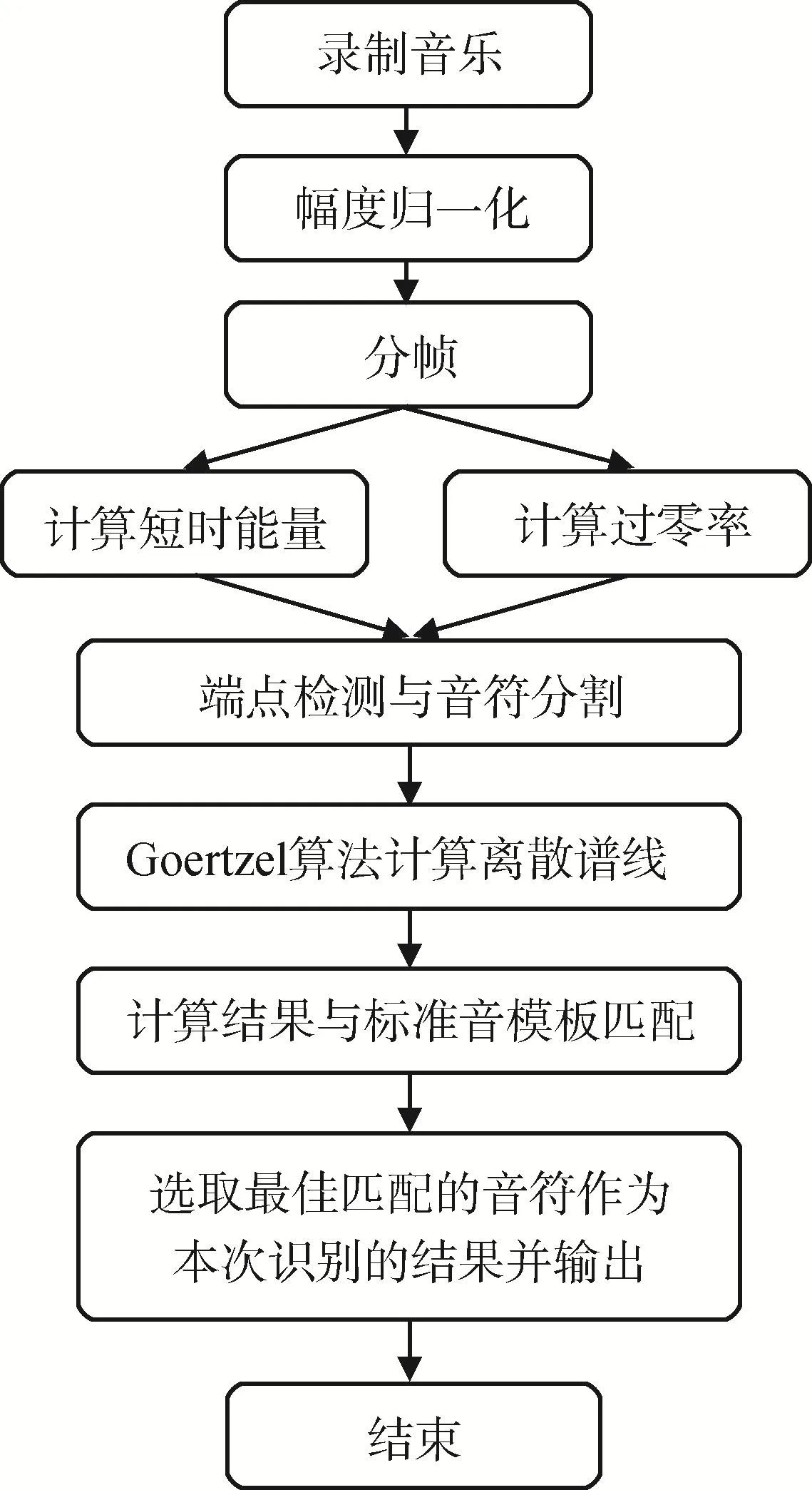
图1 音频识别算法示意图

乐音满足十二平均律,十二平均律是指按照1/12倍频程来划分音阶,每八度音为一个频程,将一个频程划分为12个半度音阶,十二平均律在数学上有严格的表示,每2个相邻的半度音阶的频率之比为2的1/12次方:

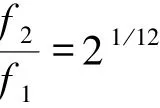
钢琴部分音符所对应的基频频率表如表1所示,一个音符唯一对应一个基频频率,单位为Hz。基音频率决定了音符的音高,也是本文识别音符的重要依据之一。

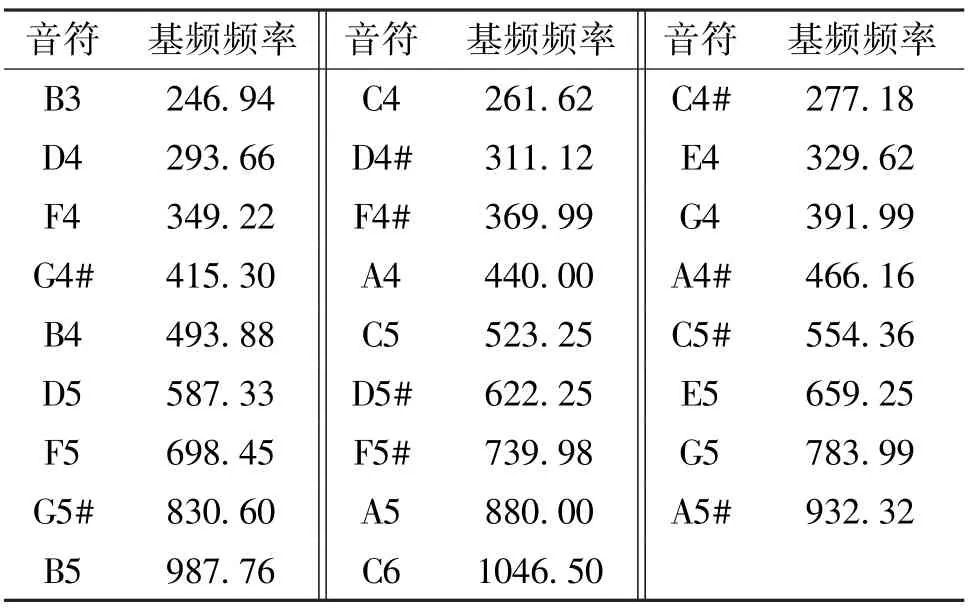
表1 钢琴部分音符基本频率表 Hz

1.2 乐音的频谱特性

如图2所示的是使用快速傅立叶变换 (FFT),以输入的C4＃信号为例绘制的频谱图像。对照表1可以看出,信号频谱在277.18 Hz基频频率处出现了较大峰值；此外,频谱在该基频频率的二次谐波和三次谐波处也出现了相当的峰值,其中二次谐波的峰值甚至大于基本频率处的峰值。一些文献中[1-2]的识别方法只保留了基频频率,这种方法固然是可行的,但放弃对泛音的利用会降低识别的抗噪性能。

图2 利用FFT算法绘制的连续频谱

实际上,虽然在高音部分的频谱特性中,谐波分量的幅度不具有突出优势；但是,在低音部分,谐波分量幅度大,利用价值明显。一种有效的方案是对每个音符的频谱做一个相应的模板,检测时只需要将待检测的信号的频谱与模板进行匹配,选择匹配程度最好的频谱作为本次识别的结果并输出。

2 音频信号的时域处理

首先,对计算机读取的音频信号的所有采样点的幅度归一化,将其转化成一标准模式；其次,乐音信号具有短时平稳特性,故在实际处理时先将乐音信号分成很小的时间段,该段就称之为“帧”,分帧的具体过程可由MATLAB自带的语音工具箱的enframe函数来实现；最后,通过短时能量和短时过零率[4]的方法判断单音符的起、止位置。

通过时域分析端点检测确定了乐音端点的起、止位置后,就可以从采集到的一段音频信号中分割出一个个单音信号(如图3所示),并逐个对分割出的单音信号进行频域分析,完成单个乐音识别,最后实现整个音频信号即乐句的识别[5]。

图3 端点检测与单音符分割结果

3 音频信号的频域分析与识别

3.1 标准音的匹配滤波器设计

利用Goertzel算法可以得到每个标准音在不同基音频率下的频谱幅度值。图2和图4以钢琴C4＃的标准音为例,分别展示了该音符利用FFT算法绘制的连续频谱和利用Goertzel算法绘制的离散谱线。

可以看出,该离散谱线几乎包含了该音符频谱峰值的全部信息。所以,可以用一个长度为N的序列S来唯一表示第i个音符的频谱特性。

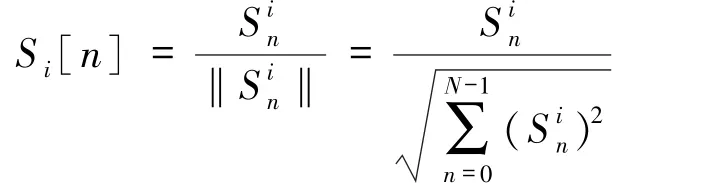
最后,将这些序列翻转时移构成M＝26路分支的匹配滤波器(对应26个示例的标准音模板),其中,n＝0,1,…,N-1；j＝1,2,…,M。则滤波器的单位冲击响应为:

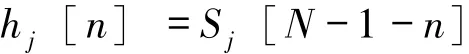
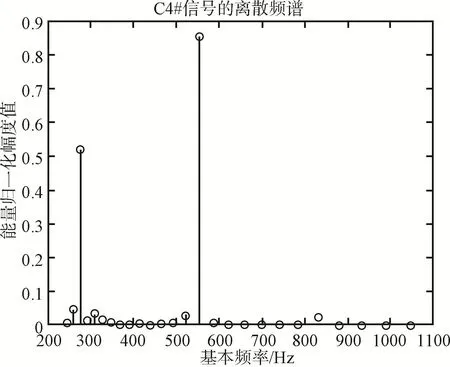
图4 利用Goertzel算法绘制的离散频谱

3.2 识别框图与原理

本文的频域识别算法示意图如图5所示。输入的音频信号经过时域处理后被分割成一个个的单音信号。将单音信号经过Goertzel算法计算后得到该信号的离散频谱序列,将这些序列并行通过M＝26路分支的标准音匹配滤波器,在卷积后的序列中点n＝N-1进行采样并输出,作为信号间相关程度的度量,把采样值最大的那一路匹配滤波器对应的音符映射输出作为输入信号的接收和识别。

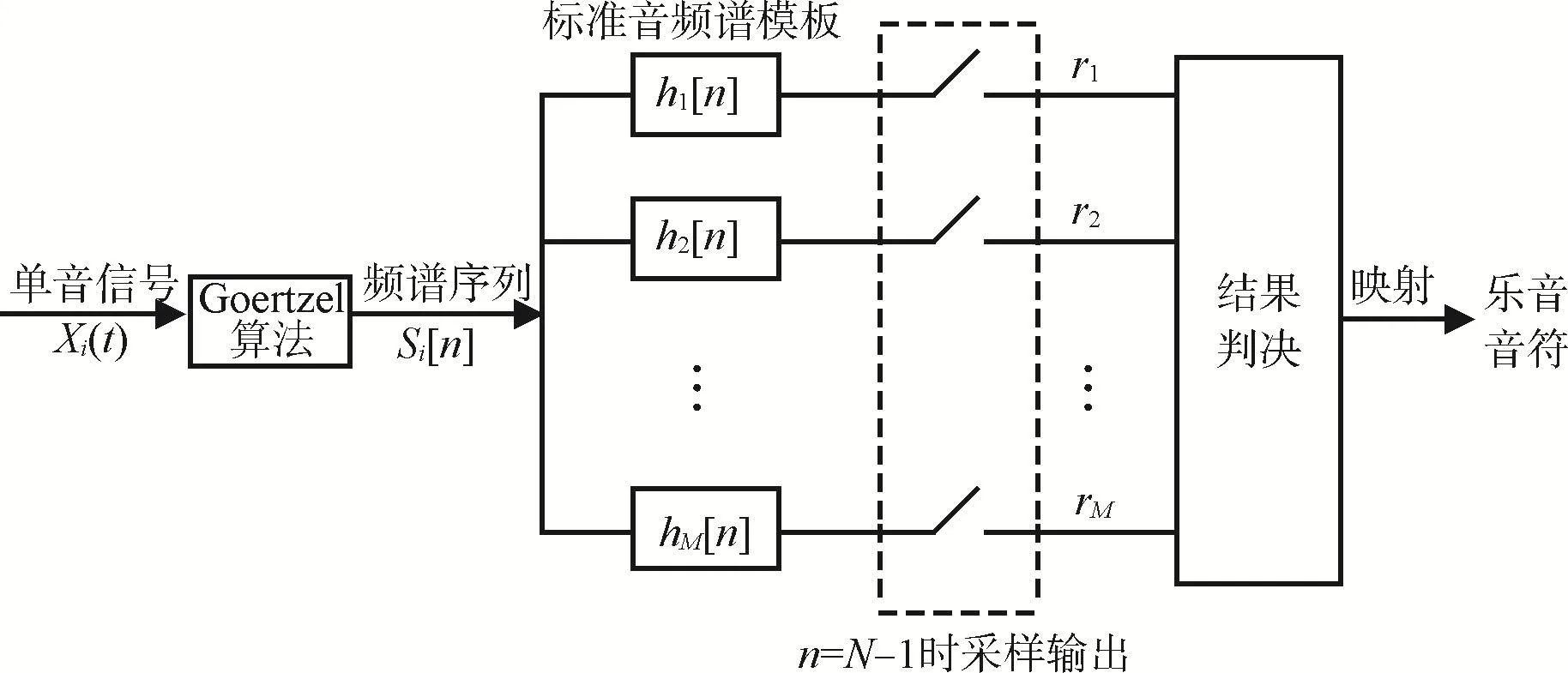
图5 单音识别算法示意图

输入单音信号Xit()的N点长的频谱序列为Si[n],各分支的匹配滤波器的冲击响应为hj[n],则输入的频谱序列通过离散匹配滤波器后采样输出的过程如下:

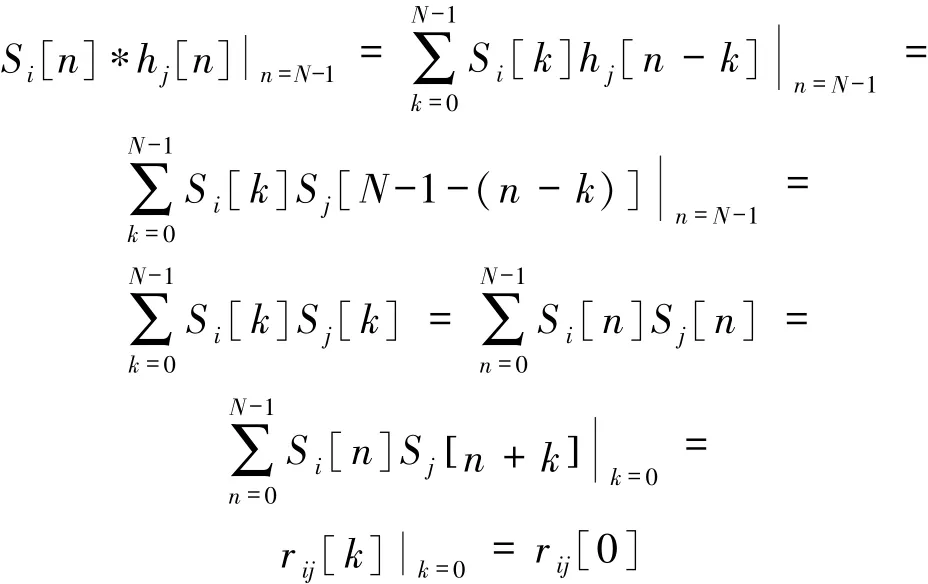
可见输入的单音信号的离散频谱序列经过匹配滤波器后采样输出的过程等效于进行相关运算[6],是输入信号与标准音信号频谱之间相关程度的一种度量[7]。因此,可以将这个相关性的度量作为乐音检测和识别的依据。

下面简要说明离散谱线能量归一化的原因。Si[n]为输入单音信号Xit()的离散频谱序列,设ri为Si[n]通过Xit()所对应的标准音匹配滤波器后的采样输出值,rj为Si[n]通过其他标准音的匹配滤波器后(i≠j)的采样输出,则有:

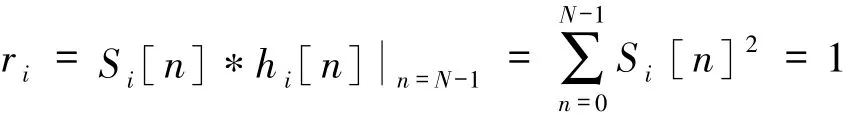
故在离散谱线能量归一化的条件下,输入的单音信号的频谱总是与其本身所对应的标准音的频谱具有最大的相关性,故能够准确判决和识别出输入的单音信号。

3.3 单音符识别的过程与结果分析

实际录音的C4信号的归一化离散频谱,以及其通过C4标准音信号的频域匹配滤波器和任一其他标准音信号的匹配滤波器后的输出序列如图6所示。图中红色(n＝26)的点为采样后的输出样本值。可以看出信号通过其本身的频域匹配滤波器后的输出样本值远大于该信号通过其他标准音信号的频域匹配滤波器的输出样本值。

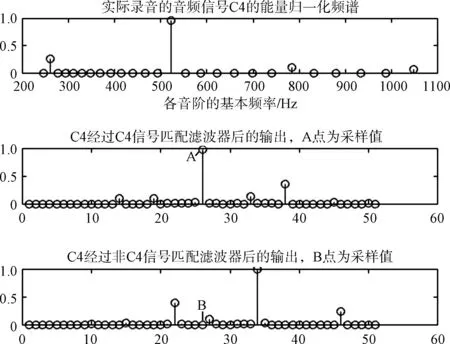
图6 频域分析的中间过程

对中音区音阶C4～B4(不含半音)采用上述乐音识别方法的识别结果如表2所示。表中的第一行代表一个待检测的实际录音音符,第一列代表相应的标准音频谱模板,表格中的数值代表行列信号之间的频谱匹配即相关程度。

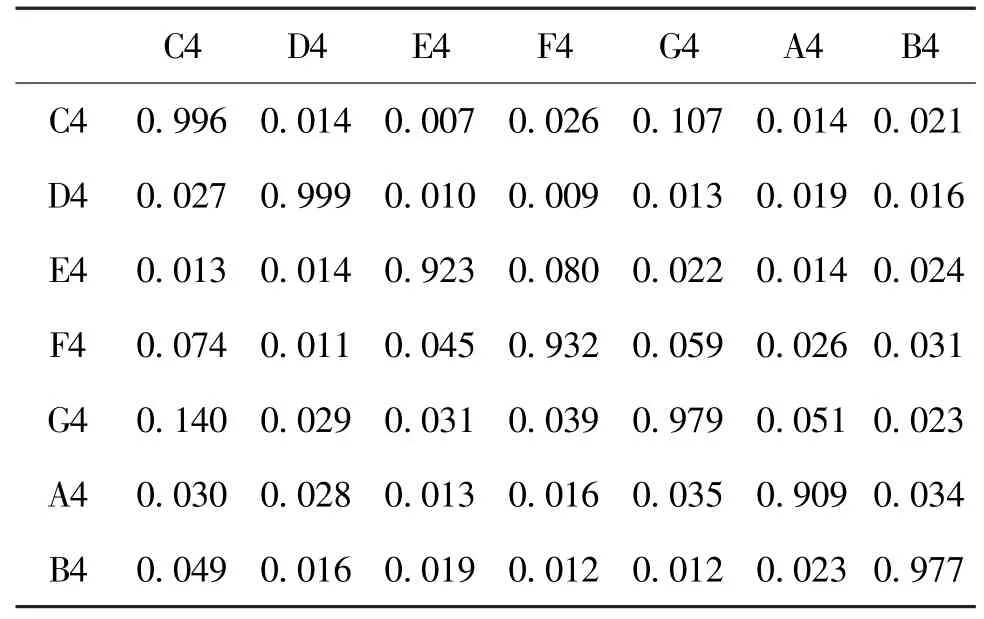
表2 待测音符与标准音频谱模板的相关程度

如表2中的对角线所示,输入的单音信号与其对应的标准音信号的频谱相关程度远大于该信号与其他标准音信号的相关度。所以很容易通过计算和比较待测信号与标准音模板之间的匹配程度识别出待测的音符,从而实现乐音的自动识别、录入和自动乐谱创作。

4 频域匹配滤波的应用

乐音识别是实现自动谱曲的基础,在音乐创作中有很重要的实用价值。下面将从实际乐音编辑和处理中较为常见的和弦分解和乐句识别这两部分,介绍频域匹配滤波的应用。

4.1 和弦的分解

和弦识别是指对3个(及以上)的乐音按一定顺序排列产生的音程组的分解和识别。接收机接收到和弦信号后,用其频谱分别与每个单音符的频谱模板进行匹配,并选择相关程度最大的前3个(及以上)音符进行输出就可以实现对和弦的分解。表3示例的是以实际录音的三音和弦(由C4-E4-G4组成)为例,进行分解的一个典型实验。可以看出,以上算法准确地实现了对该和弦的分解与识别。

表3 和弦信号与单音模板的相关程度

4.2 乐句的识别

通过对输入的音频信号进行多次端点检测,将输入的长乐句按短时能量和过零率分割成一系列的单音信号,并依次通过频域匹配滤波器进行识别,最后按序输出即可完成对整个乐句的分解和识别。

手机钢琴演奏软件演奏的乐曲 “Mary Had a Little Lamb”开始的7个单音符的波形以及检测输出结果如图7所示,录音乐句总长为20个音符,录音环境可近似认为是无噪的。

图7 乐句检测输出结果

该7个音符对应的乐谱如图8所示,对应的音符依次为:E4,D4,C4,D4,E4,E4,E4—。实验表明,检测结果与乐谱一致,系统正确识别出了乐句中所有单音符的音名,效果比较理想。

图8 被检测乐句的乐谱

由于实际应用中环境噪声的存在是不可避免的,所以下面有必要对以上算法的实际抗噪性能进行定量的分析。在该由20个音符组成的乐句的基础上,利用MATLAB的awgn函数对其加入不同强度的高斯白噪声,信噪比由该函数的SNR参数设置。同一信噪比下对乐句进行10次测试取平均,观察在不同信噪比下,该检测方法的检测准确率。实验结果如表4所示。

表4 不同信噪比下乐句的错检概率

可以看出对于加性的高斯白噪声,其信噪比为0～5 dB时,时域波形已经几乎完全失真无法辨识；而该噪声对信号的频谱影响相对较小,所以基于频域匹配滤波的识别方法仍具有很好的识别效果,即具有很好的抗噪性能。

5 结束语

本文通过对乐音信号进行时域处理和频域分析,对乐音识别进行了初步的探索,乐音识别的基本目标得到了实现。该接收和识别方法相比一些文献中进行小波变换并滤除泛音分量的识别方法[1-2]而言,充分利用了音符的泛音分量,从而增加了检测结果的可靠性；对所有可能出现频谱峰值的频率处利用Goertzel算法得到的单一谱线进行表征,相比其他一些特征表示方法[8-12],则降低了运算的复杂度；同时实际检测过程中背景噪声对离散谱线的影响相对较小,因而具有良好的抗噪性能。

本文的工作得到电子科技大学教学改革项目“通信工程大类专业挑战性课程探索”与 “探索式小班教学课程-通信原理”的支持。