面向天线互耦效应抑制的波束预编码算法

仲伟志，徐 磊，朱秋明，陈小敏，周建江

(1. 南京航空航天大学 航天学院, 江苏 南京 210016；2. 南京航空航天大学 电子信息工程学院, 江苏 南京 210016)

毫米波通信作为一种新兴的通信技术被广泛关注和研究[1]．与传统无线通信技术相比，毫米波通信具有丰富的频谱资源[2]，为实现千兆传输速率创造了条件．但是，由于超高的通信频段，毫米波无线通信面临着传播损耗高的问题．为了弥补传播损耗，毫米波通信利用在较小天线模块上形成大规模阵列天线，以实现波束赋形，从而提高天线的方向性和增益，改善链路质量[1-3]．

但是，毫米波大规模阵列天线系统中，天线阵元间的距离较小，易产生互耦效应，导致天线方向图畸变[4-5]．因此，需要通过改进波束成形方法来抑制互耦效应带来的影响．

毫米波波束成形目前吸引了大量研究者的注意，在已有的研究工作中，文献[6]提出了数字模拟混合的波束成形系统，通过信道估计和迫零法产生了具有强方向性、高增益的波束，有效地提高了用户通信质量．在此基础上，文献[7]提出了一种基于正交匹配追踪(Orthogonal Matching Pursuit，OMP)算法的混合波束预编码方法，该方法利用OMP算法进行自适应波束设计，在保证波束增益的前提下，降低了训练开销．文献[8]利用前者的结论，提出了一种面向较大蜂窝区域的宽波束优化方案，使波束能量在较大范围内近似均匀分布，保证了蜂窝内用户的通信质量．此外， 文献[9]还对波束训练协议进行了深入研究，为毫米波波束成形系统在蜂窝网络中的实际应用奠定了基础．

但是，以往研究并没有考虑天线互耦效应对毫米波系统性能的影响，这将会为实际应用带来额外误差．因此，笔者在已有研究的基础上，结合天线互耦效应分析，提出一种基于改进OMP算法的波束预编码方法，能有效地抑制互耦效应带来的波束畸变，从而提高系统性能．

1 系统模型

1.1 混合波束成形系统

文中以基站下行链路作为研究目标．为了简化计算，假设发射端采用的是数字与模拟混合的毫米波阵列系统，接收端采用单天线结构[8]，混合波束系统结构如图1所示．

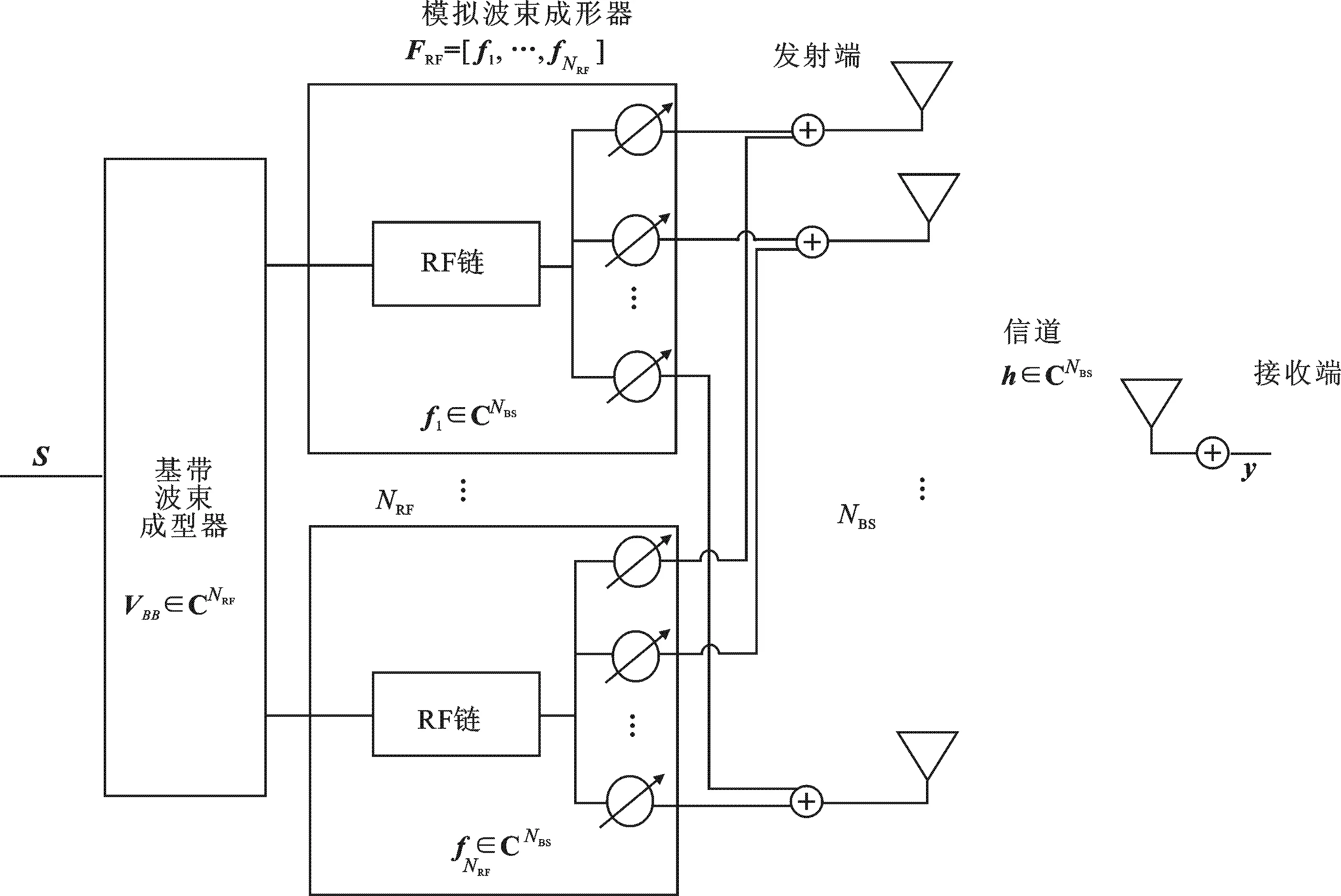
图1 混合波束成形系统

发射端由NRF个射频链路组成，控制NBS根天线产生波束，并且满足NRF≤NBS．因此，在块衰落信道下，接收信号可以表示为

y=ρ1/2hHcs+n,

(1)

(2)

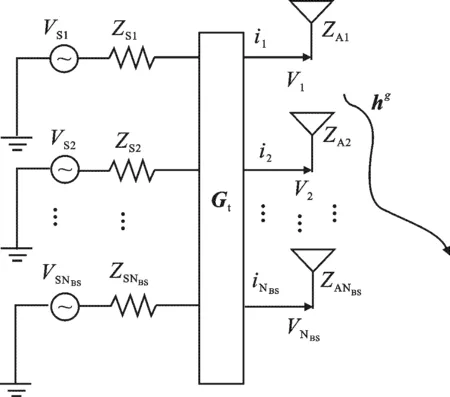
图2 等效互耦模型

1.2 天线互耦模型

当天线阵元间距很小时，每个阵元上的电压信号会感应出电流信号，从而激励产生出一个新磁场，影响相邻阵元上的信号，导致天线阵列中的天线方向图发生畸变，这种现象被称为互耦效应[10]．根据图1的发射端天线阵列结构，可得到如图2所示的等效互耦模型．图中ZA1，ZA2，…，ZANBS表示发射端的天线自阻抗，Vj(j=1，2，…，NBS)为发射端天线阵列端口电压，ij为阵列端口电流;VS1，VS2，…，VSNBS表示发射天线的电源电压值，ZS1，ZS2，…，ZSNBS为发射端电源阻抗，Gt表示发射端互耦矩阵，hg表示计算互耦效应时的信道矩阵．

天线馈电点的等效电压可表示为

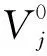
(3)

Vj=-ijZSj+VSj．

(4)

(5)

(6)

(7)

从而可以得到发射端的互耦矩阵为

(8)

由此可知，对于任意阵列流型，假设各天线特性相同，负载阻抗相等，发射端互耦矩阵可化简为

Gt=(ZS+ZA) (ZS+Zt)-1,

(9)

其中，ZS和ZA分别表示负载阻抗和天线自阻抗的值．

1.3 互耦效应下的信道模型

毫米波信道以直视路径为主，因此，信道一般可以建模为一条直视路径和多条非直视路径(Non-Line-Of-Sight， NLOS)的和[8]．假设信号传输过程中产生了L个散射信道，信道之间相互独立，在考虑互耦效应下，信道状态系数h就可以表示为

(10)

其中，K为莱斯因子，ai是满足高斯分布的复信道增益，L表示NLOS信道个数，变量θi∈ [-π，π]，表示不同信道的信号发射角(Angle Of Departure， AOD)，dBS(θi)表示基站发射角的阵列响应向量，并与天线阵列结构有关．

由于毫米波信道中的K值比较大，散射路径可以忽略不计[8]，因此，式(10)可以简化为如下形式:

h=γ(NBSNMS)1/2a0dBS(θ0)Gt,

(11)

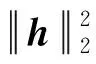
(12)

其中，d为阵元间距，λc表示毫米波信号的波长．根据式(11)的互耦信道状态系数，以IEEE.802.15.3C标准中波束设计方案为例，波束的两种可能畸变情况如图3所示．

图3 互耦效应下的波束畸变

图3(a)中的波束畸变表现为受互耦效应影响，原波束设计方案产生了巨大的旁瓣，从而大大降低主瓣增益并造成信号干扰;图3(b)中的波束畸变表现为主瓣发生了偏转，从而使目标用户增益受损，影响通信质量．不难发现，在实际通信过程中，由于阵元间的互耦效应，造成波束畸变发生，受主瓣增益降低与旁瓣干扰变大的影响，与理想情况相比，通信速率将严重下降．为了保证波束形状和方向不发生改变，需要利用互耦信道进行波束预编码，从而抑制互耦效应产生的影响．

2 基于改进OMP的预编码算法

文中提出的预编码方法以保证通信速率最大为目标，通过采用基于改进OMP的预编码方法，找到最优的模拟波束控制矩阵FRF和基带波束成形向量vBB，从而产生互耦效应下的理想波束，实现低功耗下的波束优化．

令波束预编码矢量为c，则传输速率可以定义为

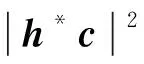
(13)

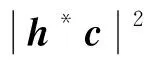
copt=γ(NBSNMS)1/2a0dBS(θ0)Gt

(14)

时，R可以获得最大取值．

根据前文可知，混合波束成形预编码的设计问题可以建模为寻找最优模拟波束控制矩阵FRF和基带波束成形向量vBB的问题[12]，即

(15)

混合波束成形方法中采用的RF链的数量远远小于天线数，因此，相比于纯数字波束成形方法，混合波束成形降低了元件损耗[7]．文中的RF链相移器将采用qbit 控制相位加权[13]，因此，式中fRF∈CNBS模拟波束成形矢量的相位集合可以表示为Zq= {0，2π/2q，…，2π(2q- 1)/2q}．

为了解决式(15)中的优化问题，文献[6]提出了基于OMP算法的解决方案，为了降低运算复杂度和元器件损耗，笔者对传统OMP算法进行了改进．以往的OMP算法中，往往需要预设非完备字典集，并在此字典集中选取FRF的新列向量fn，字典集的不完备性造成了较低的迭代速率和较高的运算次数．而在文中算法中，fn将直接由迭代残差量化而成．因此，相较于原OMP算法方案，改进算法具有更高的精确度，具体算法流程如算法1所示．

算法1 OMP波束预编码算法．

Require:copt

3 性能仿真

为了验证文中波束预编码方案的实际性能，需要进行仿真分析．假设采用阵元数目为16的ULA阵列，阵元间距为半波长，并采用传统默认的互耦参数[5]．此外，传输信道为高斯衰落信道，波束移相器由q=3 控制，发射信号功率为 0.1 W．

3.1 互耦效应抑制

由图3不难发现阵元互耦对波束形状的影响，为了量化波束畸变对通信速率的影响，需要计算功率相同情况下的系统归一化通信速率．如图4(a)所示，曲线分别为无互耦情况、存在互耦情况(不采用波束优化)下通信速率变化图，不难发现，由于阵元互耦的影响，通信速率显著下降．图4(b)验证了在NRF=2 和NRF=4 情况下，文中预编码算法对通信速率的优化作用．如图4所示，随着迭代次数的增加，文中所提出的算法几乎完全抑制了互耦效应下的波束畸变与速率降低的现象．

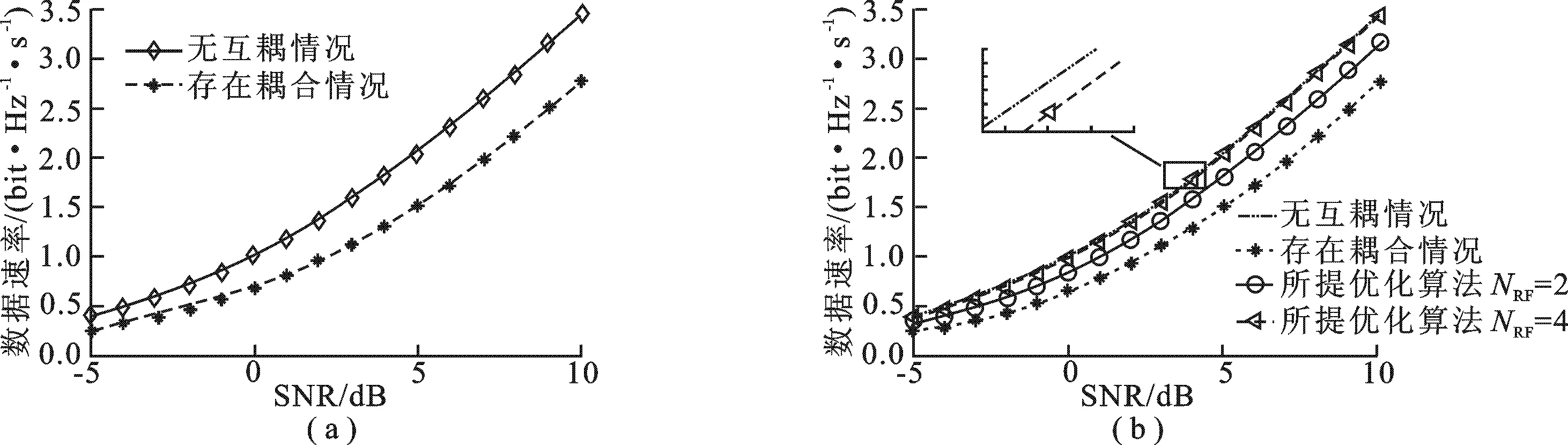
图4 通信传输速率

3.2 算法性能评估

文中采用的波束预编码算法运用了更精确的字典集，相比较于传统OMP算法具有更高的收敛速率与更优秀的迭代性能．为了验证这一点，将AOD角度域(0，π)分成M份，每一份间隔为 π/M．若角度θm(m=1，2，…，M)对应增益Q(θm)，那么增益矩阵Q可以表示为

Q=[Q(θ1)，Q(θ2)，…，Q(θm)] ．

(16)

采用变量波束畸变百分比r表示角度域内增益矩阵Q的畸变情况，那么

(17)

其中，Qq，NRF表示互耦导致波束畸变后的增益矩阵，而NRF表示迭代次数，若不采用优化设计，则NRF=0．不同迭代次数下的波束畸变百分比如表1所示．可以发现，当NRF为0的情况下，波束的畸变率较大; 而随着迭代次数的增多，波束的畸变逐渐得到抑制．相比较于传统OMP算法，文中提出的改进OMP算法在第2次迭代时取得了前者6次迭代下相近的互耦抑制效果，即文中提出的改进算法能够有效降低迭代次数，提高收敛速度，能够在一定程度上减少运算复杂度．

表1 不同迭代次数下的波束畸变百分比

4 结 论

针对毫米波大规模天线阵列存在互耦效应这一问题，文中提出了一种基于改进OMP算法的波束预编码方法．该方法以等效互耦信道模型为基础，以最大化传输速率为目标，利用改进的OMP算法求得最优预编码向量，从而获得互耦效应下的理想波束．仿真表明，文中提出的改进波束预编码方法能够有效抑制互耦效应下的波束畸变，与传统OMP算法相比，文中提出的改进算法能够大大缩减迭代次数，获得更好的畸变抑制效果．