水电站上机架-定子机座系统模态及稳定性研究

邓亚新，张 帆，杨 斌，顾承庆，李冬冬

（国网新源水电有限公司新安江水力发电厂，杭州 311608）

0 引言

研究水力发电机组重要部件的自振特性是研究其振动问题的基础，对其关键部件进行模态分析不仅有助于机组振动故障诊断，而且可以防止共振现象的发生，对保障机组安全稳定运行具有重大意义[1]。

某水电站有9台单机容量95 MW、额定转速150 r/min的混流式机组，为二导结构悬式机组，上机架为承重机架。首台机组于1960年开始发电，9台机组服役期都超过50年，机组主要承重结构部件上机架及定子机座没有进行详细的受力计算分析，且通风系统曾进行改造，在定子机座环板上开过孔，为保证机组安全稳定运行，有必要对上机架-定子机座系统振动特性进行研究。

1 上机架-定子机座结构特点

上机架主要由8条对称支臂和中心体构成，8条支臂通过螺栓联接固定在定子机座上环板。图1所示为上机架-定子机座3D模型，上机架最上端安装推力轴承座板，共10块，对称支臂最外端距离为9 840 mm。定子机座高度2 930 mm，壳体最大直径9 980 mm，主要由7层环板和40条竖直立筋构成。

在这种结构中，上机架-定子机座系统受力主要有结构自身重力、电磁场的电磁扭矩、电磁场的偏心磁拉力等。上机架放置在定子机座上，定子机座须承受上机架重量、自重和电磁扭矩。上机架-定子机座系统作为机组重要的支撑部件，除具有足够的强度和刚度外，还必须具有良好的动力特性，其模态特性将影响到机组安全性和稳定性，特别是对机组转动部分和轴承系统的稳定运行起着决定性作用[2]。

图1 上机架-定子机座3D模型

2 上机架-定子机座模态分析

2.1 模态分析原理

有限元模态分析是将某个无限复杂的多个自由度振动结构离散成多个多自由度结构，并用有限个相互独立的物理坐标重新定义结构的物理参数。各个振动都包括一种固定形态的自由振动，系统具有的固有振频就是振动频率，系统的固有振型就是振动形态[3-4]。

实际求解结构的模态特性，常做如下假设：结构的质量和刚度不变，不考虑阻尼作用，结构作自由振动。其控制方程：

式中：M，X和K分别为质量矩阵、阻尼矩阵和刚度矩阵。

对于单个线性系统，自由振动可表示为如下的简谐形式：

式中：Φi和ωi分别为第i阶振型的特征向量和自振频率；t为时间。

将式（2）代入（1）可得：

可以求得n个满足式（3）的ω2值，n为自由度。那么自振频率可表示为：

2.2 上机架-定子机座有模态分析

定子机座除鸽尾筋材料为Q345外，上机架-定子机座其余材料均为Q235，其弹性模量为210 GPa，泊松比为0.3，密度为7.85 g/cm3，边界条件为：上机架与定子机座上环的连接视为刚性连接，定子机座与水泥基础之间的连接同样视为刚性连接[2]。

采用ANSYS Workbench软件计算分析，根据上机架-定子机座的结构特点、有限元计算的精度和求解时间等，建模计算时忽略上机架-定子机座结构中的小圆角、倒角、退刀槽、砂轮越程槽等；因安装上螺栓后螺栓孔刚度加强，因此忽略所有的螺栓孔，也避免了划分网格时出现畸形网格。经过简化后，Workbench建模后的单元总数110 954，节点数228 496。

2.3 模态计算分析

应用Workbench默认的求解器，采用LANCZOS法对上机架-定子机座系统进行前6阶自振特性计算分析，提取模型固有频率和固有振动形态见表1。由表1可知，前6阶固有频率值相邻两阶十分接近，这是由于系统结构对称导致的。

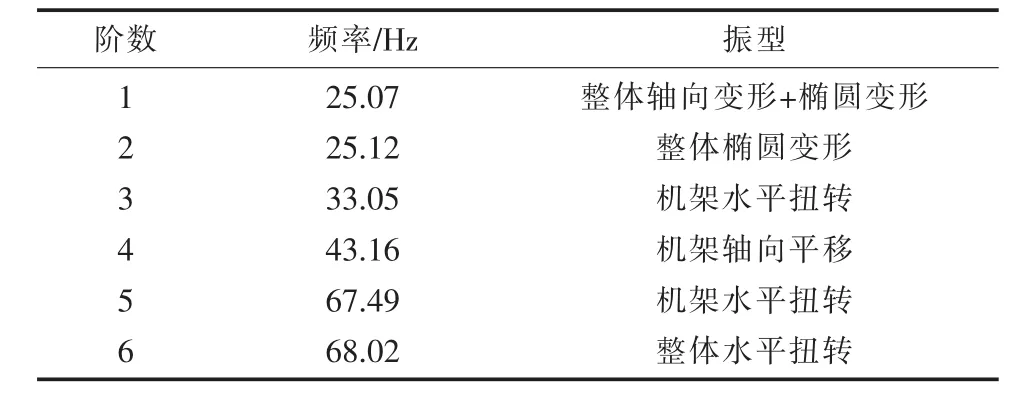
表1 上机架-定子机座系统固有频率与振型

图2为上机架-定子机座1-6阶振型，由图中结果可以看出，上机架-定子机座系统振动形态主要有整体轴向平移、椭圆晃动、水平扭转、机架水平扭转、平移，实际仿真出的自振频率为25 Hz， 33 Hz， 43 Hz和 68 Hz。

3 机组稳定性分析研究

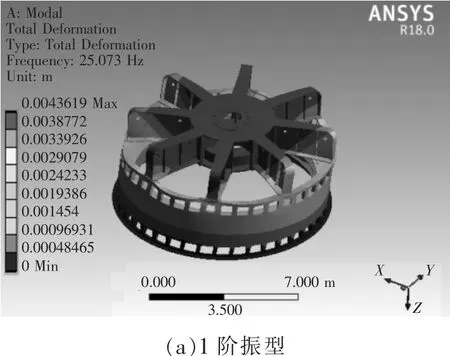
图2 上机架-定子机座1-6阶振型

表2 水轮机常见故障特征

水轮发电机系统振动故障可分为水力、机械和电气3方面[1，6-9]，具有复杂性、耦联性、故障和特征非一一对应性等特征。其常见故障特征如表 2 所示[1，6-15]。

根据机组结构参数，转频fn为2.5 Hz，推力轴承数量m为10，活动导叶Z0数量为24，计算可得机组故障特征频率为：2.5 Hz，25 Hz，60 Hz，0.69 Hz。卡门涡列的特征频率通常在100～500 Hz，且很少出现[6]。从以上计算可知，只有推力瓦不平整的特征频率（25 Hz）与理论模态频率接近。推力瓦不平整的主要原因是推力头和轴颈间有间隙，轴和推力头之间有相对运动现象，这种现象非常少见[8]。

4 结论

上机架-定子机座系统理论模态频率为25 Hz， 33 Hz， 43 Hz， 68 Hz， 只有 25 Hz与机组常见故障特征频率接近，但此种故障极其少见。机组上机架-定子机座系统结构稳定，不会产生常见共振故障，可以保证机组安全稳定运行。