单列高速列车通过隧道空气阻力特性数值模拟研究

杨永刚，杜云超，梅元贵



单列高速列车通过隧道空气阻力特性数值模拟研究

杨永刚，杜云超，梅元贵

(兰州交通大学 甘肃省轨道交通力学应用工程实验室，甘肃 兰州 730070)

针对高速列车空气阻力直接影响列车最高运行速度，采用真实外形的8编组国内某型动车组，建立单车通过隧道的数值计算模型，并对隧道空气阻力的形成机理及其随时间的变化特性、列车表面压力与阻力两者变化间的关系、列车各部件阻力的分布特性进行分析；对比隧道通过时整车阻力的最大值、最小值和明线整车的阻力值。研究结果表明：列车通过隧道时，隧道内压缩波和膨胀波对列车阻力有直接影响，列车空气阻力呈现准周期性波动，其中压差阻力的波动幅度比摩擦阻力的波动幅度大；压差阻力和摩擦阻力所占的比例随时间而变化；列车空气阻力的最大值和最小值分别为明线的1.96倍和0.89倍。列车明线稳定运行时，压差阻力和摩擦阻力分别占列车空气阻力的61.7和38.3%。列车通过隧道过程中，列车各部件阻力分布特性随时间而变化。

高速列车；隧道空气阻力；形成机理；分布特性

近年来，随着高速列车速度的快速提高，列车空气动力学问题成为高速列车发展的关键问题，其对高速列车的运行经济性、安全性、舒适性和周围环境有着重要影响。高速列车通过隧道时，空气动力学问题更为严重，高速列车空气阻力直接影响列车的最高运行速度。近年来，国内外学者通过实车试验、模型试验、数值模拟等方法对高速列车空气动力学特性进行了大量研究[1−11]，对高速列车隧道空气阻力的研究相对较少。Nakade等[12−13]采用三维数值模拟方法将列车明线稳定运行和隧道单车通过时气动力的波动幅度进行了对比，说明列车气动力波动的原因，展示了气动力沿列车长度方向的波动规律，以及列车通过隧道时，空气阻力的变化特性。Takanobu等[14−15]采用三维数值模拟方法研究了高速列车隧道内会车时空气阻力随时间的变化特性，车速和阻塞比对空气阻力最大值的影响。王伟等[16]建立了隧道内空气阻力的计算公式，讨论了不同隧道断面的阻力系数。LI等[17−18]介绍了运用动模型实验测试列车在明线运行和隧道通过时的空气阻力。赵有明等[19]介绍了一种隧道内非恒定流空气附加阻力实车试验测试技术。Peters等[20]研究了ICE/V列车隧道因子随列车长度和隧道长度的变化情况但是上述研究对列车通过隧道时空气阻力的形成机理、随时间的变化特性、分布特性没有进行详细研究。本文采用8编组国内某型动车组，研究单车通过隧道时，空气阻力的形成机理及其随时间的变化特性，隧道内压缩波和膨胀波对压差阻力、摩擦阻力影响；列车表面压力变化对列车空气阻力的影响，车体各个部件的阻力分布特性。列车通过隧道时空气阻力的最大值、最小值以及明线运行时的阻力值进行对比研究。

1 计算模型和网格划分

1.1 计算模型

列车采用8编组国内某型动车组，列车外形及几何尺寸如图1所示。

(a) 正视图；(b) 受电弓

取轨面到车顶平面高度4.05 m为基准尺寸，记为，车体总长为51.6。隧道采用《高速铁路设计规范》(TB10621—2009)时速300 km/h和350 km/h双线隧道，隧道净空面积100 m2，线间距5.0 m。忽略隧道线路沿列车运行方向的坡度，隧道内的线路为直线，并且忽略隧道内的轨道、竖井等结构，隧道长度取800 m。

1.2 计算区域

计算区域如图2所示，隧道长度记为L。图中为隧道内轮廓直径，=13.3 m。

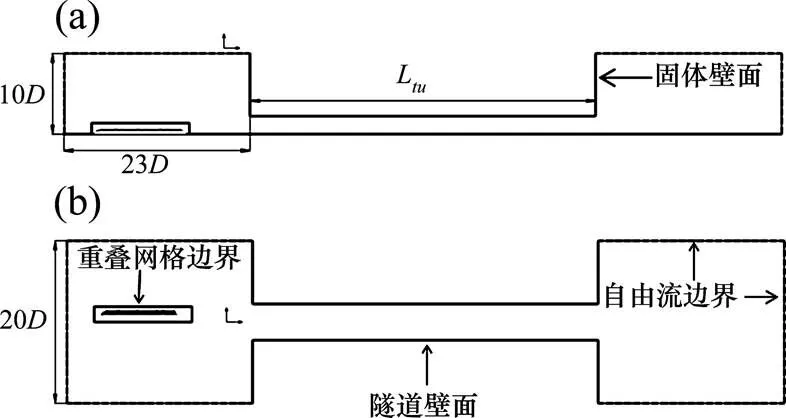
(a) 侧视图；(b) 俯视图

1.3 网格划分

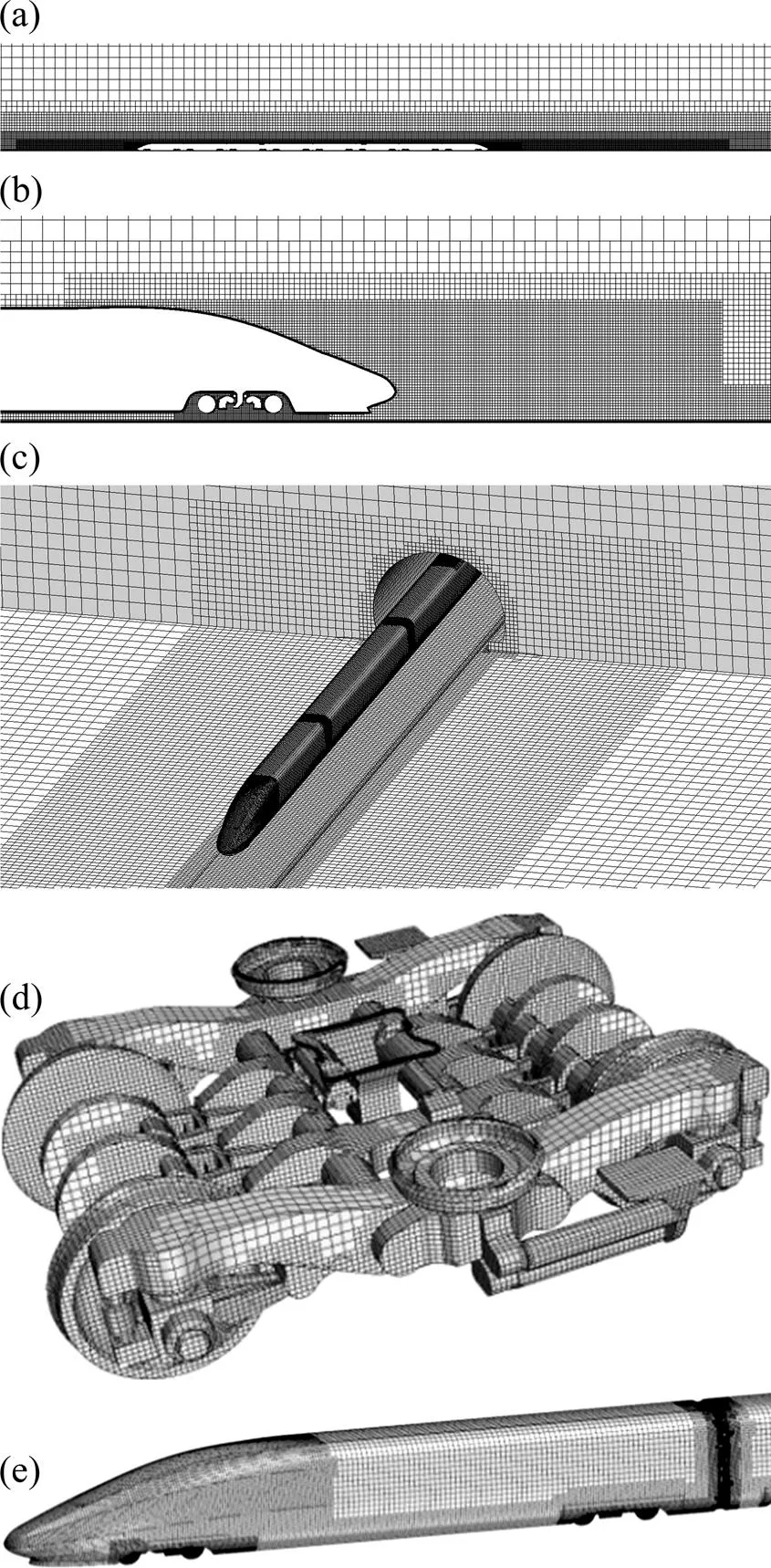
(a) 网格整体分布；(b) 尾流区网格；(c) 隧道口网格；(d) 转向架表面网格；(e) 列车头部(尾部)网格

1.4 计算方法

列车过隧道时，隧道内的空气流动十分复杂，空气流动受到隧道壁面的限制而被压缩，流场处于湍流状态，计算采用三维、非定常、可压缩N-S方程，湍流模型为SST−模型，应用重叠网格技术对高速列车通过隧道时的空气阻力进行数值模拟研究。根据重叠网格和非定常计算对时间间隔的要求，计算时间步长取0.001 s，为保证每步计算达到收敛，内迭代次数为20。

对于单车过隧道情形，列车表面和隧道表面、隧道口的垂直边界、路基表面为无滑移固体壁面，其切向速度都设定为0。开阔空间的其他边界均采用自由流边界，用于模拟无穷远处的可压缩流动。

计算参数：列车运行速度350 km/h，远场压力取1 013 025 Pa，参考温度取283 K。

1.5 气动力系数定义

阻力系数和压力系数定义如下：

阻力系数：

压力系数：

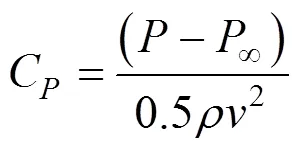
式中：为空气密度，1.225 kg/m3；为来流速度、列车运行速度；为参考面积，取列车方向的横截面积11.93 m2；F为空气阻力。

根据CEN标准[21]，隧道因子的定义如下：

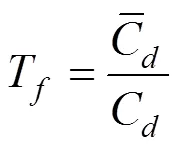
2 方法验证

文中分别采用高速列车风洞试验的阻力和实车通过隧道压力波的结果验证本文所采用的数值模拟方法的合理性和准确性。

2.1 风洞验证

为验证本文所采用网格划分的可靠性。本文通过与CRH380A缩尺风洞测试结果进行验证。风洞试验中来流风速为60 m/s，侧偏角为0。风洞试验采用的模型为1:8缩尺模型，带有转向架、路堤、钢轨、支柱及风挡，实际风洞的截面尺寸为8 m×6 m。本文所使用计算域截面尺寸与风洞相同，并在流向方向进行延长以降低尾流对计算结果的影响。

表1 列车阻力系数值

数值模拟结果与风洞试验测试结果如表1所示。由表1可知：空气阻力的误差最大值为10.7%。

2.2 重叠网格方法验证

为验证本文所采用的计算方法的合理性。本文通过与京沪线凤凰台隧道实车试验数据进行验证。实车试验中，列车采用8编组，列车速度300 km/h，隧道长1 168 m。实车试验与数值计算的压力时间历程曲线如图4所示。由图4可知：数值模拟计算所得测点的压力与现场实测的压力变化规律基本一致，最大误差为6.5%。

图4 隧道内200 m处测点的压力波对比

综合风洞试验和实车试验可知：本文所采用的计算方法和网格划分方法可用于求解列车过隧道的空气动力学问题。

3 计算结果与分析

3.1 列车空气阻力形成机理

图5表示列车通过隧道的压力、阻力时间历程曲线。图5(a)表示列车运行轨迹、压缩波和膨胀波的传播轨迹。其中：“”表示压缩波，“”表示膨胀波。图5(d)中蓝色曲线为阻力系数，红色直线为隧道内列车阻力系数的平均值。0时刻车头端到达隧道端口。

(a) 传播轨迹；(b) 头车鼻尖测点压力；(c) 尾车鼻尖测点压力；(d) 阻力系数

由图5可知：车头驶入隧道前，列车表面的压力和列车阻力都处于稳定状态。0时刻，车头到达隧道口，产生初始压缩波N1并向隧道出口方向传播。由于隧道壁对空气流动的限制作用，车头前方的空气受到压缩，车头鼻尖的压力快速升高，由于车尾在明线运行，故尾车鼻尖压力依旧处于稳定状态，头尾车的压差增大，列车阻力突然增大。随着列车继续驶入隧道，车头鼻尖压力线性增大，阻力也平稳上升。=2.15 s时，车尾到达隧道口，产生初始膨胀波T1并向隧道出口方向传播。车尾的压力突然减小，头尾车的压差再次增大，列车的阻力再次急剧增大。车尾驶入隧道一段距离后，列车阻力达到最大值。由于车尾驶入隧道入口时产生的膨胀波强度最大，导致车尾负压值最大，而车头正压仍保持较大值，因此，在此位置列车阻力最大。

=2.15~8.23 s时，高速列车在隧道内运行，由于压缩波和膨胀波的不断传播和反射，列车阻力呈现准周期性波动。

=8.23 s时，车头驶出隧道，车头的压力增大，恢复到明线运行时的压力。列车驶出隧道过程中，膨胀波T2和压缩波N和T2相继经过车尾，使车尾的压力产生波动，导致列车驶出隧道过程中，列车阻力产生波动。列车完全驶出隧道后，列车恢复到明线运行时的阻力。8编组列车通过隧道过程中，阻力系数平均值为0.864，隧道因子为1.35。

3.2 列车表面压力和阻力两者变化间关系

图6表示列车通过隧道过程中列车截面处的压力分布。在图6(a)中，列车明线稳定运行时，在车头前方，以鼻尖为中心，形成正压区，向四周辐射。图6(b)中，=2.2 s时，车尾驶入隧道后，产生初始膨胀波T1，使车尾的压力开始下降；车头前方的压力继续增大。图6(c)中=5.0 s时，膨胀波N1经过车体，列车表面的压力和列车周围的压力下降，车体表面的负压值较大。图6(d)中，=6.6 s时，压缩波T1经过车体，列车表面的压力和列车周围的压力再次增大。图6(e)中，=9.3 s时，列车驶出隧道一半车长，驶出隧道的车体的表面压力恢复到明线运行时的压力。

3.3 列车空气阻力时间历程特征

列车通过隧道过程中，阻力时间历程曲线如图7所示。图7(a)为压差阻力、摩擦阻力和总阻力的力系数曲线。图7(b)为摩擦阻力。

(a) 明线运行；(b) 列车完全驶入隧道(t=2.2 s)；(c) 膨胀波经过车体(t=5.0 s，膨胀波EN1)；(d) 压缩波经过车体(t=6.6 s，压缩波CT1)；(e) 驶出隧道一半车长(t=9.3 s)

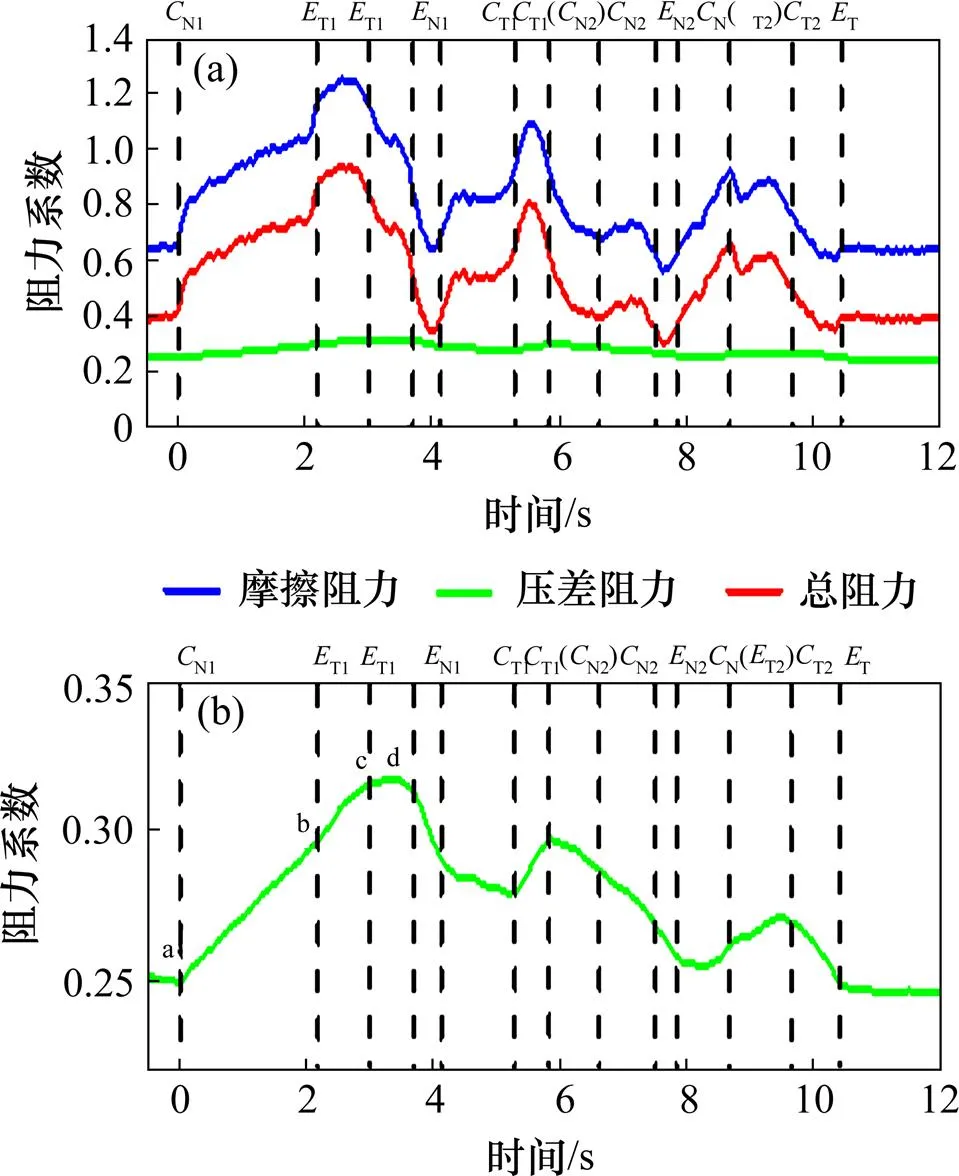
(a) 阻力时间历程曲线；(b) 摩擦阻力

在图7(a)中，列车在隧道内运行时，列车压差阻力有时小于明线的压差阻力，有时大于明线的压差阻力；但摩擦阻力一直大于明线运行时的摩擦阻力。列车的摩擦阻力和压差阻力都随时间而波动，但摩擦阻力的波动幅度小于压差阻力的波动幅度；列车阻力随压差阻力的变化而变化，两者的变化趋势几乎一致，压差阻力对列车阻力的影响远大于摩擦阻力对列车阻力的影响。

在图7(b)中a~b时刻：=0~2.15 s时，列车驶入隧道过程中，车身壁面与隧道壁面组成环状空间，随着列车的不断驶入，环状空间增大，由于空气的黏性，列车的摩擦阻力随着环状空间的增大而增大。b~c时刻：=2.15~2.7 s时，车尾完全进入隧道口后，整车的摩擦阻力还在继续增大。这主要是因为：由于列车在隧道内继续向前行驶，车头前方受挤压的空气进一步增多，车头前方压力也继续增大。这样，车头前方的空气通过环状空间向车头后方流动的空气越来越多，流动速度也越来越大，这样导致列车与周围空气的摩擦阻力也越来越大。c时刻：=3.0 s时，膨胀波T1经过车头后，车头前方的空气压力下降。这样，从车头前方流向车体后方的空气流动速度减小，摩擦阻力也开始减小。

由图7可知：列车通过隧道过程中，压差阻力和摩擦阻力都随时间而波动。为了分析摩擦阻力和压差阻力在列车通过隧道过程中不同时刻的值和所占的比例，取列车在明线、=2.7 s时列车完全驶入隧道、=5.0 s时膨胀波N1经过车体、=6.6 s时压缩波T1经过车体、=9.3 s时列车驶出隧道一半车长5个时刻的阻力进行分析。图8表示了5个时刻各个力系数值以及所占的比例。

由图8(b)可知：列车明线稳定运行时，摩擦阻力和压差阻力分别占列车空气阻力的38.4%和61.6%。列车完全驶入隧道后，压差阻力所占的比例达到最大，占列车空气阻力的75.3%。=5.0 s膨胀波经过后，列车的压差阻力所占的比例大于明线对应的比例。=6.6 s压缩波经过后，列车的压差阻力所占的比例小于明线对应的比例。=9.3 s时，列车驶出隧道一半车长，车头的压力恢复到明线运行的压力；而前一时刻，膨胀波T2经过列车尾部，车尾的压力下降，头尾车压差增大，导致该时刻列车的阻力大于明线的阻力，压差阻力所占的比例大于明线对应的比例。列车通过隧道过程中，列车的压差阻力和摩擦阻力所占的比例随时间而变化，压差阻力和摩擦阻力各自所占的比例有时大于明线的，有时小于明线对应的比例。

(a) 阻力值；(b) 所占比例

图9为列车明线单车稳定运行和通过隧道过程中整车阻力最大值和最小值时刻的阻力分布。由图可知：隧道对列车空气阻力的影响较大，特别是压差阻力。8编组列车通过隧道时空气阻力最大值为明线的1.96倍，对应时刻的压差阻力和摩擦阻力分别为明线的2.4倍和1.26倍。隧道通过时的阻力最小值为明线的0.89倍，对应时刻的压差阻力和摩擦阻力分别为明线的0.76倍和1.08倍。

图9 隧道内阻力最大值和最小值以及明线的阻力分布

3.4 列车阻力分布特性

取列车在明线、=2.7 s时列车完全驶入隧道、=5.0 s时膨胀波N1经过时的数据、=6.6 s时压缩波T1经过车体、=9.3 s时列车驶出隧道一半车长5个时刻的阻力进行分析。平直车身包含所有平直车厢的侧墙和顶部，车底包含所有车厢的底部，转向架包含所有的转向架和转向架腔，风挡包含所有风挡，如图10所示。受电弓系统如图11所示。图12表示了列车通过隧道过程中，列车各部件阻力的分布特性。表2为不同时刻，列车各部件的阻力值。

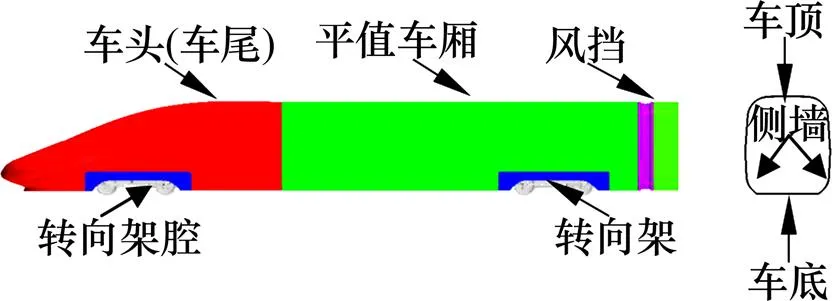
图10 列车部件示意图

图11 受电弓系统

由图12和表2可知：对于车头，阻力主要为压差阻力，列车明线稳定运行时，车头的阻力和所占的比例较小，列车驶入隧道后，车头的压力增大，压差阻力增大，车头的阻力和所占的比例增大，大于明线的阻力值和所占的比例。当膨胀波经过列车后，车头的压力减小，压差阻力减小，车头的阻力变为负值，小于明线运行时所占的比例。压缩波经过之后，车头的压力增大，车头的阻力和所占的比例增大，大于明线的阻力值和所占的比例。

图12 不同时刻列车阻力分布特性

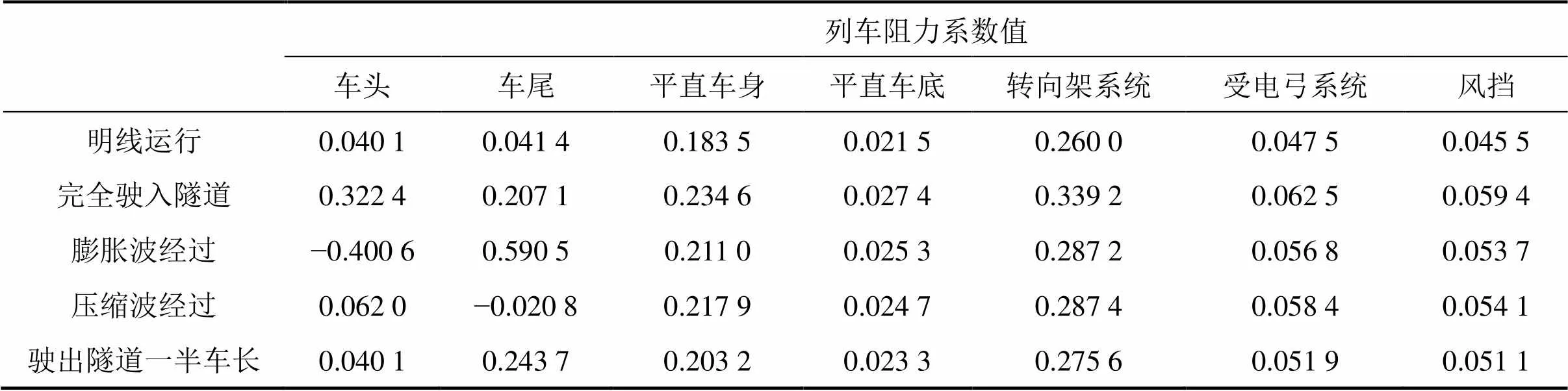
表2 不同时刻列车阻力百分比

对于车尾，阻力主要为压差阻力，列车明线稳定运行时，车尾的阻力和所占的比例较小，列车驶入隧道后，产生初始膨胀波，车尾的压力减小，压差阻力增大，车尾的阻力和所占的比例增大，大于明线的阻力和所占的比例。当压缩波和膨胀波经过车尾后，车尾的阻力与车头的阻力变化相反。列车驶出一半车长时，膨胀波T2经过车尾，车尾的压力减小，车尾的阻力和所占的比例增大，大于明线对应的阻力和阻力所占的比例。

对于平直车身和平直车底，主要为摩擦阻力，隧道内的阻力大于明线的阻力，但阻力值变化不大。但所占的比例有时小于明线对应的比例，有时大于明线对应的比例。对于转向架系统，列车完全驶入隧道后，阻力增大，大于明线对应的阻力，但所占的比例小于明线所占的比例，主要是因为车头、车尾阻力的增大幅度大于转向架系统的增大幅度。其他时刻，由于压缩波和膨胀波的作用，转向架系统的阻力和所占的比例随时间而变化。对于受电弓系统和风挡，同转向架系统一样，其阻力值和阻力所占的比例随时间而变化。

4 结论

1) 通过与实车试验、风洞试验结果对比，验证了本文所采用的计算方法和网格划分的正确性。

2) 8编组列车明线稳定运行时，压差阻力和摩擦阻力分别占总空气阻力的38.3%和61.7%；列车单车通过隧道时，列车的压差阻力有时大于、有时小于明线运行时的压差阻力，列车的摩擦阻力一直大于明线的摩擦阻力。

3) 单车通过隧道时，由于隧道内压缩波和膨胀波的反复作用，列车表面的压力随时间而变化，导致列车阻力呈现准周期性波动。压差阻力的波动幅度比摩擦阻力的波动幅度大；8编组列车通过隧道时的空气阻力最大值为明线的1.96倍；空气阻力最小值为明线的0.89倍。

4) 8编组列车明线稳定运行和隧道内运行时，转向架系统的压差阻力和平直车身的摩擦阻力占列车气动阻力的比例较大；列车通过隧道过程中，车头、车尾的阻力变化幅度较大；列车阻力的分布特性随时间而变化。

[1] 肖京平, 黄志祥, 陈立. 高速列车空气动力学研究技术综述[J]. 力学与实践, 2013, 35(2): 1−12. XIAO Jingping, HUANG Zhixiang, CHEN Li. Review of aerodynamic investigations for high speed train[J]. Mechanics in Engineering, 2013, 35(2): 1−12.

[2] ZHANG Jie, LI Jingjuan, TIAN Hongqi, et al. Impact of ground and wheel boundary conditions on numerical simulation of the high-speed train aerodynamic performance[J]. Journal of Fluids and Structures, 2016(61): 249−261.

[3] Raghunathan R S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002(38): 469−514.

[4] 梅元贵, 周朝晖, 许建林. 高速铁路隧道空气动力学[M]. 北京: 科学出版社, 2009. MEI Yuangui, ZHOU Chaohui, XU Jianlin. High-speed railway tunnel aerodynamics[M]. Beijing: Science Press, 2009.

[5] 李人宪. 高速列车气动影响[M]. 北京: 中国铁道出版社, 2016. LI Renxian. High-speed train aerodynamic effect[M]. Beijing: China Railway Press, 2016.

[6] 田红旗. 中国高速轨道交通空气动力学研究进展及发展思考[J]. 中国工程科学, 2015(4): 30−41. TIAN Hongqi. Development of research on aerodynamics of high-speed rails in China[J]. Engineering Sciences, 2015(4): 30−41.

[7] DING Sansan, LI Qiang, TIAN Aiqin, et al. Aerodynamic design on high-speed trains[J]. Acta Mechanica Sinica, 2016(2): 215−232.

[8] 刘堂红, 田红旗, 金学松. 隧道空气动力学实车试验研究[J]. 空气动力学学报, 2008(1): 42−47. LIU Tanghong, TIAN Hongqi, JIN Xuesong. Experimental study of full-scale train on aerodynamics in tunnel[J]. Acta Aerodynamica Sinica, 2008(1): 42−47.

[9] ZHANG Lei, YANG Mingzhi, LIANG Xifeng, et al. Oblique tunnel portal effects on train and tunnel aerodynamics based on moving model tests[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017(167): 128−139.

[10] MEI Yuangui. A generalized numerical simulation method for pressure waves generated by high-speed trains passing through tunnels[J]. Advances in Structural Engineering, 2013, 16(8): 1427−1436.

[11] 梁习锋, 田红旗. 列车气动性能评估参数研究[J]. 中国铁道科学, 2003, 24(1): 38−42. LIANG Xifeng, TIAN Hongqi. Research on evaluating parameters of train aerodynamic performance[J]. China Railway Science, 2003, 24(1): 38−42.

[12] Nakade Koji1, Suzuki Masahiro1, Fujimoto Hiroshi1. Interaction between vehicle vibration and aerodynamic force on high-speed train running in tunnel[J]. Vehicle System Dynamics, 2004, 41(Suppl): 717−723.

[13] 王一伟, 杨国伟, 黄晨光. 高速列车通过隧道时气动阻力特性的CFD仿真分析[J]. 中国铁道科学, 2012, 33(B8): 33−38. WANG Yiwei, YANG Guowei, HUANG Chenguang. CFD simulation analysis high-speed on the aerodynamic drag characteristics of train running through tunnel[J]. China Railway Science, 2012, 33(B8): 33−38.

[14] Takanobu Ogawa, Kozo Fujii. Numerical simulation of compressible flow induced by a train moving in a tunnel[C]// 23rd Fluid Dynamics, Plasmadynamics and Lasers Conference, 1993.

[15] 赵晶, 李人宪. 高速列车进入隧道的气动作用数值模拟[J]. 西南交通大学学报, 2009, 44(1): 96−100. ZHAO Jing, LI Renxian. Numerical analysis of aerodynamics of high-speed trains running into tunnels[J]. Journal of Southwest Jiaotong University, 2009, 44(1): 96−100.

[16] 王韦, 王建宇, 陈正林. 隧道中高速列车活塞风及空气阻力的计算[J]. 中国铁道科学, 1999, 20(1): 9−16. WANG Wei, WANG Jianyu, CHEN Zhenglin. Computation of piston wind and aerodynamic drag on high speed train in tunnel[J]. China Railway Science, 1999, 20(1): 9−16.

[17] LI Zhiwei, YANG Mingzhi, HUANG Sha, et al. A new method to measure the aerodynamic drag of high-speed trainspassing through tunnels[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2017(171): 110−120.

[18] YANG Mingzhi, DU Juntao, LI Zhiwei, et al. Moving model test of high-speed train aerodynamic drag based on stagnation pressure measurements[J]. PLOS ONE, 2017, 12(1): 1−15.

[19] 赵有明, 马伟斌, 程爱君, 等. 高速铁路隧道气动效应[M]. 北京: 中国铁道出版社, 2012: 47−124. ZHAO Youming, MA Weibin, CHENG Aijun, et al. Aerodynamic effect of high speed railway tunnel[M]. Beijing: China Railway Press, 2012: 47−124.

[20] Peters J L. Measurement of the influence of tunnel length on the tunnel drag of the ICE/V train[J]. Aerodynamics and Ventilation of Vehicle Tunnels, 1991: 739−756.

[21] CEN European Standard. Railway applications- aerodynamics. Part 1: Simbols and Units, CEN EN 14067-1[S].

Numerical simulation of aerodynamic drag of single high-speed train passing through a tunnel

YANG Yonggang, DU Yunchao, MEI Yuangui

(Lanzhou Jiaotong University, Gansu Province Engineering Laboratory of Rail Transit Mechanics Application Institute of High Speed Train Aerodynamics, Lanzhou 730070, China)

Based on the aerodynamic drag directly affects the maximum running speed of high-speed train, this paper established the numerical calculation model for single train passing through the tunnel with the real configuration of a domestic EMU with eight carriages. The formation mechanism and variation characteristics of the tunnel aerodynamic drag over time, the relationship between the changes of the car body surface pressure and the drag, the distribution characteristics of the drag of individual parts of the train were analyzed at different times of the train when passing through the tunnel. The maximum and minimum of the drag values for going through the tunnel were compared with the drag of the open air condition. Results indicate the compression and expansion waves directly affected on the drag, the drag showing quasi-periodic fluctuations over time of the whole train, the fluctuation range of the pressure drag is larger than the friction drag, the possession ration of pressure drag and friction drag are changed over time when the train passing through the tunnel. The maximum value and minimum value of total drag when the train passing through the tunnel are 1.96 times and 0.89 times of that in the open air.When the train is running in the open air, the pressure drag and frictional drag accounted for 61.7% and 38.3% respectively of the total aerodynamic drag. The distribution characteristics of the drag of individual parts of the train are changed over time.

high-speed train; tunnel aerodynamic drag; formation mechanism; distribution characteristics

10.19713/j.cnki.43−1423/u.2018.11.005

U270

A

1672 − 7029(2018)11 − 2755 − 09

2017−10−30

中国铁路总公司科技研究发展计划课题资助项目(2016T004-F)

梅元贵(1964−)，男，河南荥阳人，教授，博士，从事高速列车空气动力学研究；E−mail：meiyuangui@163.com

(编辑 蒋学东)