基于数据演绎和认知模型构建探讨化学平衡——由两道高考真题及改编题引出的深度思考
李银秀
湖南
平衡思想是高中化学核心素养之一。化学平衡保证了化学变化有限度,造就了物质的多样性,保持了化学物质在质的方面的稳定性。化学平衡是一切平衡的基础,是中学阶段重要的基本理论,也是教学的难点之一。对于一个具体的可逆反应,化学平衡状态的建立与反应途径无关,这是化学平衡的重要特征,其化学平衡常数只与温度有关,这是化学平衡的定量特征。在学习中,若能有效运用这些特征,深入运用数学模型,可深化理解化学平衡,同时提高运用多学科知识解决较复杂问题的综合能力,促进思维的深度发展,提升科学素养。根据2011年江苏高考化学卷第15题改编的一道试题,是将数学思维模型与化学认知模型充分融合的一道好题,由此也引发对2018年高考新课标理综Ⅰ卷第28题中有关化学平衡考查的深度思考。
一、 2011年江苏高考真题节选及分析

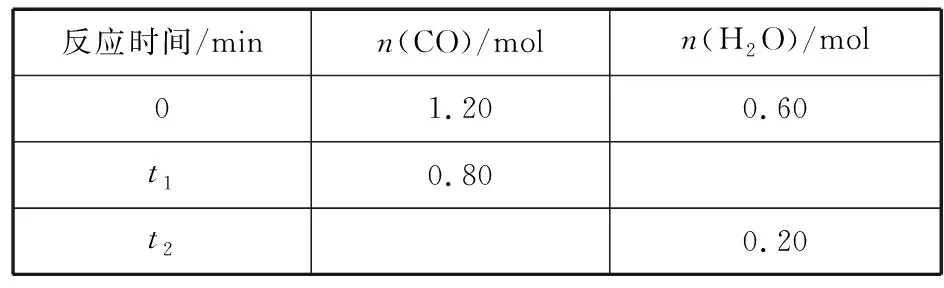
反应时间/minn(CO)/moln(H2O)/mol01.200.60t10.80t20.20
分析“保持其他条件不变,起始时向容器中充入0.60 mol CO和1.20 mol H2O,到达平衡时,n(CO2)=0.40 mol”是否正确。
分析:读取表格信息可知0~t1时间段内,CO转化物质的量为1.20 mol-0.80 mol=0.40 mol,采用三段式分析法:

n(起始)/mol 1.20 0.60 0 0
n(转化)/mol 0.40 0.40 0.40 0.40
n(t1)/mol 0.80 0.20 0.40 0.40
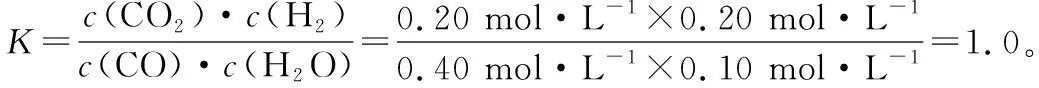
保持其他条件不变,起始时向容器中充入0.60 mol CO和1.20 mol H2O,用假设法验证:若达平衡时,n(CO2)=0.40 mol,则CO平衡时物质的量为0.60 mol-0.40 mol=0.20 mol,也采用三段式分析法:

n(起始)/mol 0.60 1.20 0 0
n(转化)/mol 0.40 0.40 0.40 0.40
n(平衡)/mol 0.20 0.80 0.40 0.40
因为温度不变,K为定值,通过假设法快速验证该说法正确。
由此可见,其他条件不变时,将CO、H2O的起始物质的量调换,分别达平衡时产物的物质的量相等。仔细分析K的表达式,不难发现,原因在于化学平衡常数只与温度有关。
二、2011年江苏高考改编题及分析
(2011年江苏高考化学卷第15题改编题)在一定温度下,在相同密闭容器中,分别充入氢气、碘蒸气2 mol、1 mol和1 mol、2 mol,达到平衡时,两密闭容器中碘化氢的物质的量是否相同?为什么?
分析方法一:该题与2011年江苏高考化学卷第15题 B选项非常相似,都是一个反应前后气体物质的量不变且两种反应物的化学计量数相等的反应。基础比较好的同学完全可以类比迁移2011年江苏高考化学卷第15题的结论直接判断出两种情况下碘化氢的物质的量相等。但该题的亮点在于要写出证明过程,增加了思维深度,而且要将抽象思维外显,增大了试题的区分度。在教学中,许多学生觉得证明过程有难度,似乎只可意会不可言传。本文巧妙借助平衡常数相等,深入运用数学思维模型,详细展示证明过程,以提升学生的证据推理和模型认知核心素养。
为了证明题中的数据2 mol、1 mol和1 mol、2 mol并非是固定不变的一组特殊数据,假设两组数据分别为任意比值,I2、H2的物质的量分别设为1 mol、nmol和nmol、1 mol(设n大于1),容器体积为VL,用三段式分析法:

n(起始)/mol 1n0
n(转化)/molaa2a
n(平衡)/mol 1-an-a2a

n(起始)/(mol)n1 0
n(转化)/(mol)bb2b
n(平衡)/(mol)n-b1-b2b
因为温度相同,化学平衡常数相等,K1=K2,所以有
4a2[n-(n+1)b+b2]=4b2[n-(n+1)a+a2]
a2[n-(n+1)b+b2] =b2[n-(n+1)a+a2]
na2-(n+1)a2b+a2b2=nb2-(n+1)ab2+a2b2
na2-(n+1)a2b=nb2-(n+1)ab2
na2-nb2-(n+1)ab(a-b)=0
n(a+b)(a-b)-(n+1)ab(a-b)=0
(a-b)[n(a+b)-(n+1)ab]=0
①
因为可逆反应中反应物的转化率小于100%,故有0
②
根据②式,将①中因式[n(a+b)-(n+1)ab]中较大值(a+b)用较小值ab代换,得到:
2nab-(n+1)ab=ab(2n-n-1) =ab(n-1)
③
因为n>1,0
④
根据①式和④式,可知必有a-b=0,可得:a=b,2a=2b。
即假设n>1时,两种情况下碘化氢的物质的量相等。
同理可证明0 若n=1,两种情况下每种反应物的物质的量对应相等,达到的自然是完全相同的平衡状态,不需要证明。 这种分析方法周密严谨,大多数学生比较容易接受。 2018年3月19日,教育部基础教育司专家到我校调研时强调,教育不是追求每个学生的整齐划一,而是尽量让不同天赋、不同程度的学生得到最大限度的个性发展。为此,若是基础比较好的学生,还可以进一步深度运用数学思维模型,通过证明函数在给定区间内的单调性,来证明本题的结论。 ① ② ③ ④ 只要证明在定义域x∈(0,1)内f(x)为单调函数,即每改变一个n的值,x为唯一确定的值,结果即得证;而要证明x∈(0,1)内f(x)为单调函数,需要证明x在(0,1)内的导函数恒为正数或恒为负数,因此需要求f(x)的导函数。 根据求导公式:(Kx2)′=K·2x、(xn)′=nxn-1和③式 因为平衡常数K为正值,分母K(1-x)2恒为正值,由于x∈(0,1),所以4x(2-x)>0,即f′(x)>0恒成立。 可见f(x)>0,f′(x)>0,故f(x)在(0,1)区间内单调递增,即碘单质与氢气在题给条件下调换起始物质的量,产物碘化氢的物质的量一定相同。 同理可证明当0 当然,第二种方法虽比第一种方法复杂,但对学生综合性思维的培养、引导他们自觉将不同学科知识融合,不孤立用单一学科思维方式思考问题。比如,用数学的眼光看世界,看到的是舍弃了内容的数和形,用化学的眼光看世界,看到的是物质之间的联系和变化。将各种眼光结合起来,才有可能看到一个完整的“图象”。这是全面、深入认识世界所必须秉持的态度和方法。注重知识的横向联系,打破学科之间的壁垒,对于培养学生的核心素养具有重要意义。 以上试题着重考查对于一个具体的可逆反应,其浓度平衡常数只与温度有关的特征;近年高考题,也非常重视分压平衡常数的考查,下面以2018年高考新课标理综Ⅰ卷第28题为例进行分析。 (2018年新课标理综Ⅰ卷第28题节选)采用N2O5为硝化剂是一种新型的绿色硝化技术,在含能材料、医药等工业中得到广泛应用。回答下列问题: (2)F.Daniels等曾利用测压法在刚性反应器中研究了25℃时N2O5(g)分解反应: 2N2O4(g) 其中NO2二聚为N2O4的反应可以迅速达到平衡,体系的总压强p随时间t的变化如下表所示[t=∞时,N2O5(g)完全分解]: t/min040801602601 3001 700∞p/kPa35.840.342.545.949.261.262.363.1 分析:该小问考查分压平衡常数的计算,对完整理解化学平衡理论有重要意义。因为前几年新课标卷如2014年新课标理综Ⅰ卷第28题曾以信息形式提到:用平衡分压代替平衡浓度计算,分压=总压×物质的量分数。根据理想气体状态方程pV=nRT,可知等温等容下,气体的分压之比等于气体的物质的量之比,故此题中不再呈现该完整信息。因为平衡状态的建立与反应途径无关,在计算过程中可以采用多种不同的思维模型计算出p(NO2)、p(N2O4),进而求出Kp,体现了对证据推理与模型认知核心素养的考查,也间接考查了对化学平衡状态的建立、化学平衡状态的理解和应用。另外,该题信息t=∞时,N2O5(g)完全分解,意在暗示N2O5的分解达到化学平衡需要足够长的时间,隐含了温度一定时,随着反应的不断进行,浓度减小,反应速率递减的规律;启示学生理解工业上的许多可逆反应不一定追求化学平衡状态,同时深刻领会学习外界条件对化学平衡的影响,主要是创设条件,促使平衡(化学平衡、电离平衡、水解平衡、沉淀溶解平衡等)向人们期待的方向移动,也体现了对变化观念与平衡思想核心素养的考查。 p(起始)/kPa 35.8 0 0 p(∞)/kPa 0 35.8×2 35.8÷2 p(起始)/kPa 71.6 0 p(转化)/kPa 2xx p(平衡)/kPa 71.6-2xx 因为t=∞时,p(总)=63.1 kPa,即p(O2)+p(NO2)+p(N2O4)=63.1 kPa (17.9+71.6-2x+x)kPa=63.1 kPa 解得:x=26.4 kPa 71.6-2x=71.6-2×26.4=18.8 kPa 分析方法二:从原子守恒角度出发,题中反应可拆分为下列两个反应,用守恒法分析: 根据前述分析可知:p(NO2)+p(N2O4)=p(总)-p(O2)=63.1 kPa-17.9 kPa=45.2 kPa 根据反应前后氮原子守恒可知:p(NO2)+2p(N2O4)=2×35.8 kPa=71.6 kPa 解得:p(NO2)=18.8 kPap(N2O4)=26.4 kPa 2 kPa (4-2x) kPaxkPa 1 kPa 35.8 kPa 35.8(2-x) kPa 17.9xkPa 17.9 kPa 因为t=∞时,p(总)=63.1 kPa,即17.9+35.8(2-x)+17.9x=63.1 kPa 解得:17.9x=26.4 即35.8(2-x)=71.6-35.8x=71.6-52.8=18.8 即:p(NO2)=18.8 kPap(N2O4)=26.4 kPa 分析方法四:从原子守恒角度出发,题中反应可拆分为下列两个反应,用极端假设法分析。 ① ② 但实际发生反应①②,设发生反应①②的N2O5(g)的物质的量分数分别为x、1-x,则根据t=∞ 时,p(总)=63.1 kPa,可列式:89.5x+53.7(1-x)=63.1 通过以上不同角度分析方法,可帮助学生从多种角度认识N2O5分解的实质,建立灵活多变的化学平衡思维模型,其实质都是反应前后质量守恒,平衡常数只与温度有关。该大题对化学平衡的原理应用进行了全方位、多角度的综合考查,涉及了信息的接受、吸收和整合(表格数据理解分析、方程式选用等),文字表达,计算等,设问层层递进,能力层层筛选,是全卷非常靓丽的一道风景线。尤其是该小问和最后一问,能很好区分学生核心素养上的差异。湖南省答卷该题抽样情况如下表1。 2018年高考新课标理综Ⅰ卷第28题湖南省答卷抽样统计表1 抽样数:205315 样品总数:205316 平均分(含零/不含零):3.54/3.74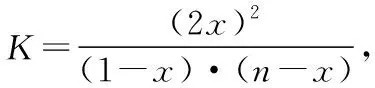
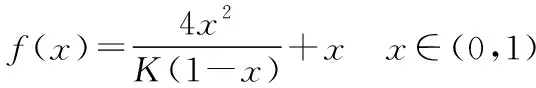
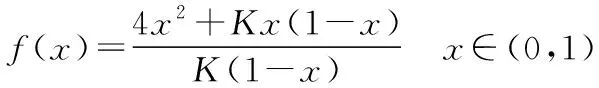
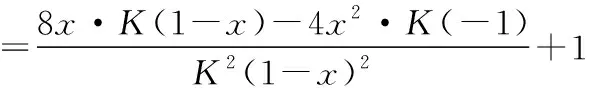

三、2018年高考新课标理综Ⅰ卷真题节选及分析














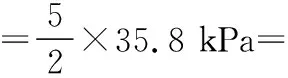

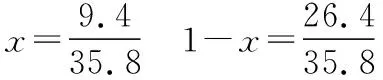
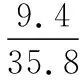
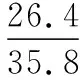


四、教学启示


