工业区土壤高光谱特性及其重金属含量预测研究——以上海市闵行区为例

陈银莹，柳云龙, *

1. 上海师范大学地理系，上海 200234；2. 上海师范大学城市生态与环境研究中心，上海 200234

土壤反射光谱中隐藏着土壤信息，不同反射波段的反射值是不同土壤特性综合信息的反映。分析土壤高光谱特性并利用其研究土壤问题，已广泛应用于土壤方面的研究（黄淑玲等，2015；赖宁等，2015；Casa et al.，2012）。随着工业化进程发展，大量重金属污染物通过各类生产排放进入土壤中，由于重金属不易被分解、易在土壤中富集，导致土壤重金属污染（蔡茜茜，2018；迟光宇等，2017；Li et al.，2017）。且由于工业区受人为干扰强烈，污染源众多，重金属污染呈现种类多、差异大、空间分布变异大等特点，使得监测难度上升（蒋煜峰等，2015；李小平等，2010）。传统的实验室重金属含量测量方法虽然能够获取较高测量精度，但采样效率低下且无法获取连续的空间信息，在对重金属污染源众多、重金属分布空间异质性高的工业区的研究中，传统的研究方法无法较好地满足对工业区土壤重金属含量的检测。

国内外研究发现，利用土壤光谱反射率反演预测土壤重金属含量，较之传统的实验室测定方法，具有便捷快速、大批量、低成本、对土地破坏性低的特点（Lewis et al，2004；Viscarra et al.，2007）。一般地，自然环境中的土壤重金属含量较低，并且对土壤光谱反射率在可见光-近红外反射波谱内的影响微弱，甚至没有任何影响（郭颖等，2018；Alloway，2013）。因此通过直接分析土壤重金属元素的光谱特征来估算其含量的工作难以进行。然而，工业区受人类活动影响强烈，如工业生产排放、生活垃圾排放、汽车尾气排放、汽车零部件磨损等，土壤中重金属元素富集现象严重，较高的含量使得利用土壤高光谱进行土壤重金属含量预测成为可能。此外，土壤中富集的重金属元素与土壤中有机质、粘土矿物、铁锰氧化物、碳酸盐矿物等土壤组分存在一定相关关系——主要为吸附与赋存作用，使土壤组分对光谱反射率有所影响，为在可见光-近红外反射波谱内间接预测土壤重金属元素含量提供可能性参考（程先锋，2017；Pinheiro et al.，2017），这是高光谱遥感探究土壤重金属含量的机理所在。国内外研究表明，利用可见光-近红外光谱能够进行较大面积的土壤重金属含量反演估算（王维等，2011；Tan et al.，2014；吕杰等，2015），但由于各研究区土壤类型不同，所受气候、成土母质、生物以及人为活动影响不同，土壤物质组成具备差异性；且该物质本身的独特光谱特征会导致土壤所反映的特征波段位置不同，同时由于各研究所采用的反演模型不同，导致最优模型的选择也有所差异（Kooistra et al.，2001；张威等，2014；张龙龙等，2015）。

在对多种土地利用类型，包括矿区、河流沉积区、郊区等区域的土壤重金属的研究过程中，偏最小二乘回归模型（Partial Least Squares Regression Model，PLSR）是利用土壤光谱反演土壤重金属含量最常用的模型，一般适用于变量多而样本少的数据；多元逐步回归线性模型（Stepwise Multiple Linear Regression Model，SMLR）则是最为传统的拟合模型，拟合过程自动剔除影响不明显的变量，直接选择具备突出影响的变量作为输入变量进行拟合。多项研究表明，这两种模型均能够满足较大区域的土壤重金属含量反演需求，适用于本研究中变量多的数据特点（Shi et al.，2013；Shi et al.，2014；王菲等，2016；郭颖等，2018）。目前利用受强烈人为干扰的工业区土壤光谱反演土壤重金属含量方面的研究为数不多，本研究选取上海闵行区西南部工业区土壤重金属为研究对象，分析工业区土壤的光谱特征，确定反演土壤重金属 Cu、Cr、Mn、Pb、Zn的特征波段，并采用偏最小二乘法及多元逐步回归线性法建立重金属高光谱预测模型，探讨在城市工业区中利用高光谱数据估算土壤重金属含量的适用性。

1 材料与方法

1.1 土壤样品采集

研究区为上海市闵行区西南部工业区（121°22′E，31°00′N），总面积 3.5 km2。重点发展机电产业（轨道交通、电站设备），以医药疗产业（常用药物）和轻工业（食品饮料）为辅。根据研究区域内地形分布、土地利用与覆盖的状况，在数字底图上通过网格布点大致确定采样点和取样数，使采样点分布相对均匀。实际取样时，根据工业区内工业企业、建筑物和道路的实际分布特点，对采样点数量和空间分布进行适度调整，土壤采样深度为0～20 cm，采样点GPS精确定位，共采集土壤样品63个。采样点分布如图1所示。样品带回实验室后，经风干、碾碎、过100目筛后，密封保存备用。将样品分为两份，一份用于高光谱测定，一份用于重金属含量分析。

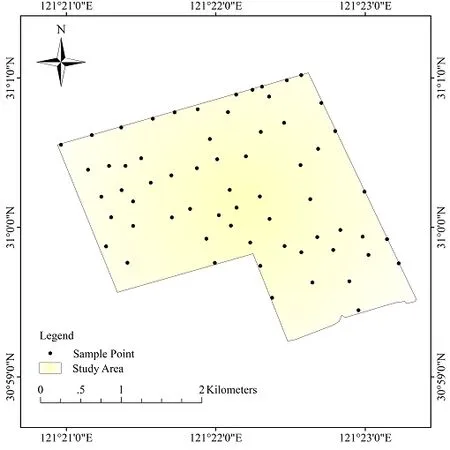
图1 研究区土壤采样点分布图Fig. 1 Distribution of soil sampling points in the study area

1.2 土壤样品光谱反射率与重金属含量测定

土壤样本的反射光谱使用荷兰 Ava Field-2便携式高光谱地物波谱分析仪采集，波段范围在300～1700 nm。在300～1040 nm范围内采样间隔为0.59 nm，在1040～1700 nm范围内采样间隔为3.8 nm，光谱分辨率为5 nm，输出波段为1421个。选取预处理后的2 cm样品放入直径为10 cm的器皿内，为减少因土壤样品表面凹凸不平所产生的散射光影响所测精度，对样品表面进行刮平处理。选择距离土壤表面20 cm的能够提供平行光的卤光灯作为光源，探头采用 15°光源照射角度、5°视角场和15 cm探头距离，同时利用标准白板进行定标，获取绝对反射率。为减少测量不稳定性所带来的误差，每个土样采集 10条光谱曲线，去掉异常光谱曲线后取平均值，得到的平均值作为土壤样品的实际反射光谱数据。采用X荧光分析检测法进行土壤Cu、Cr、Mn、Pb、Zn全量分析，该方法具有制样简便、可分析种类多、无损、快速、准确的优点，能够同时检测多种金属元素且不产生废弃物（王世芳等，2016；王鑫等，2018；Bilo et al.，2017；侯张明，2016；钟山等，2014）。

1.3 光谱数据预处理

光谱测定过程中由于光谱仪或外界其他光源的干扰会产生误差，为消除背景噪声、增大原始光谱曲线的特征、减弱原始数据的误差，需要对数据进行平滑处理及数据变换，以提高光谱的性噪比（吴明珠等，2014）。利用 ENVI（Exelis Visual Information Solutions，Boulder，CO，USA）软件对光谱数据进行平滑处理与包络线去除处理，把反射率进行归一化处理（0～1），消除光谱曲线背景噪音，突出光谱特征值。对光谱数据进行低阶微分变换能够有效去除背景漂移与基线干扰，放大原始数据所表达的信息，突出土壤原始光谱隐藏的反射特征。本研究对原始光谱数据进行一阶微分（First Derivative，FD）、二阶微分（Second Derivative，SD）、均方根一阶微分（Root Mean Square First Derivative，RMSFD）、均方根二阶微分（Root Mean Square Twice Derivative，RMSTD）、倒数一阶微分（Reciprocal Transformation First Derivative，RTFD）、倒数二阶微分（Reciprocal Transformation Second Derivative，RTSD）、倒数对数一阶微分（Absorbance Transformation First Derivative，ATFD）、倒数对数二阶微分（Absorbance Transformation Second Derivative，ATSD）共8种变换形式的处理（张秋霞等，2017；吴明珠等，2014；Shi et al.，2013）。

2 结果与讨论

2.1 土壤光谱曲线特征分析

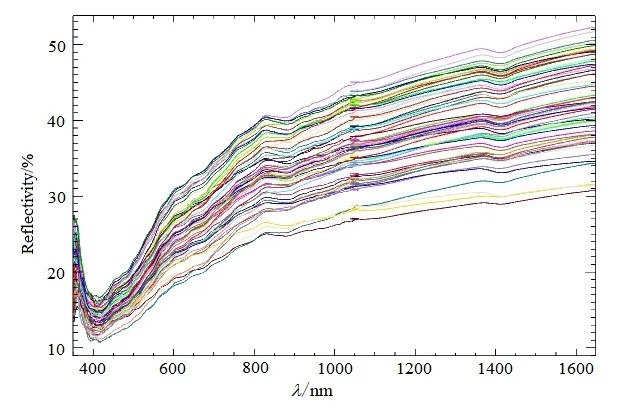
图2 研究区样本点土壤光谱曲线走势图Fig. 2 Spectral curve of soil in sampling points in the study area

为减少光谱测定过程中所产生的误差和数据记录的冗余、增强相似光谱之间的差别，需要对原始光谱进行平滑处理，处理后的 63个样本点光谱曲线走势见图 2。土壤光谱曲线基本走势大致分为4种基本类型，包含平直型（富含有机质的土壤）、缓斜型（与水耕热化联系的水稻土）、陡坎型（富铁铝土壤）、波浪型（干旱地区土壤）（戴昌达，1981）。由图2可知，63个样点土壤光谱反射率在10.01%～50.20%之间变化，土壤光谱反射率曲线基本平行且缓慢抬升，走势基本一致，均属于缓斜型。光谱曲线在可见光区域增加较快，在近红外区域增加缓慢。光谱曲线在近红外区域差异较大。土壤有机质和铁氧化物对其产生的影响主要在可见光和近红外波段，土壤含水量的增加使光谱反射率下降（徐彬彬等，1991）。图3(a)所示为样本光谱曲线去包络线图，经处理的光谱曲线突出显示了光谱的吸收特征和反射特征。在可见光至部分近红外（400～1650 nm）谱段内，受铁氧化物的影响，最低反射率出现在409.55 nm处。总体光谱反射率的吸收谷出现在425 nm处，吸收深度为0.43。在825～900 nm谱段受有机质的影响存在 C-H吸收带，在1400～1425 nm谱段受粘土矿物中所含OH-基团和H2O的影响存在结晶水的吸收峰（程先锋等，2017；江振蓝等，2017）。图3(b)所示为63个样点中重金属含量最高与最低样点的光谱反射率及平均光谱反射率图，重金属含量最高的样点光谱反射率低于重金属含量最低的样点光谱反射率，重金属含量最低样点的光谱反射率在400～600 nm之间，低于平均反射率（600～840 nm），二者反射率几乎相等，840 nm之后虽然重金属含量最低样点的光谱反射率略低于平均反射率，但仍十分接近。这些差异性可作为分析土壤反射光谱与重金属关系的基础（肖捷颖等，2013）。

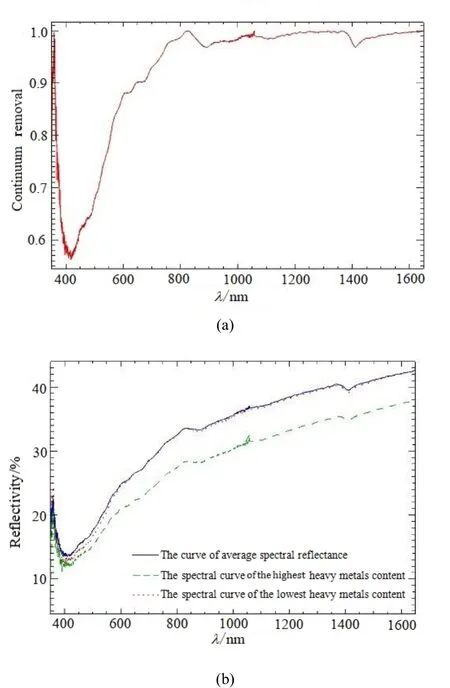
图3 样点光谱去包络线图和研究区重金属含量最高与最低点光谱曲线以及所有样点平均光谱曲线图Fig. 3 Sample spectrum to the envelope graph and the spectral curves of the highest and lowest soil samples in the study area and the average spectral curves of all sample

2.2 土壤重金属含量统计分析

对工业区土壤重金属含量进行统计分析，结果如表1所示。由表1可知，土壤重金属Cu、Cr、Mn、Pb、Zn含量平均值依次为 29.38、106.32、583.14、34.13、111.15 mg·kg-1，工业区土壤重金属平均含量均超过上海市土壤环境背景值。变异系数表示各样点重金属含量的平均变异程度，在一定程度上能反映样品受人为影响的程度。工业区土壤中Cr、Mn变异系数较小，分别为0.13、0.18，说明这两种元素受外界影响比较一致，空间分异相对较小。土壤Cu、Pb、Zn的变异系数分别为0.6、0.86和0.55，空间分异较大，说明土壤Cu、Pb、Zn受外界干扰比较显著，易受到较强的工业生产排放、交通运输等人为活动因素影响（蒋煜峰等，2015）。对土壤5种重金属含量进行相关分析，分析结果如表2所示。由表可知，土壤 Cu与 Pb、Zn，土壤Pb与Zn的含量在0.01水平呈显著相关，土壤Cr与Mn在0.05水平呈显著相关，表明工业区土壤重金属之间表现为复合污染或者具有同源性，多数土壤样品被2种以上重金属元素污染（韩玉丽等，2015）。

2.3 土壤重金属含量与光谱相关性分析

为了获取土壤重金属含量与反射光谱之间的关系，对土壤重金属含量与土壤光谱数据不同变换形式进行相关性分析。通过相关系数的大小确定特征波段范围及最优特征波段，结果见表 3，特征波段将作为反演因子进行数据建模。总体而言，原始光谱数据经微分变换后能够在某种程度上提高其与重金属含量的相关性，但不同重金属与不同光谱变换数据的相关性不同，特征波段也不同。土壤重金属Cu与二阶微分光谱变换数据相关性最强，特征波段范围在1088.17～1440.21 nm，最优特征波段为1440.21 nm。土壤重金属Cr与方根二阶微分光谱变换数据相关性最强，特征波段范围在584.06～985.52 nm，最优特征波段为834.44 nm。土壤重金属 Mn与倒数一阶光谱变换数据相关性最强，特征波段范围在 756.22～1047.57 nm，最优特征波段为984.98 nm。土壤重金属Pb与方根二阶微分光谱变换数据相关性最强，特征波段范围在1372.65～1440.21 nm，最优特征波段为 1440.21 nm。土壤重金属Zn与二阶微分光谱变换数据相关性最强，特征波段范围在1011.18～1649.15 nm，最优特征波段为1642.50 nm。一般认为，原始光谱的低阶微分能够放大数据特征，提高其与重金属含量的相关性（于庆等，2018；贺军亮等，2015）。本研究中，Cr、Mn、Pb含量与光谱原始数据的方根低阶微分变换、倒数低阶微分变换以及对数低阶微分变换之后的相关性更强，也能够用于反演模型的建立，这能够为光谱数据预处理提供新的参考方法。5种重金属的最优特征波段均在近红外波段范围内，但不同重金属的最优特征波段位置不同，特征波段范围也不一致，这与工业区内土壤组分受强烈人为活动影响较复杂，以及不同土壤组分对不同重金属的吸附与赋存作用不同有关（张静静等，2018）。

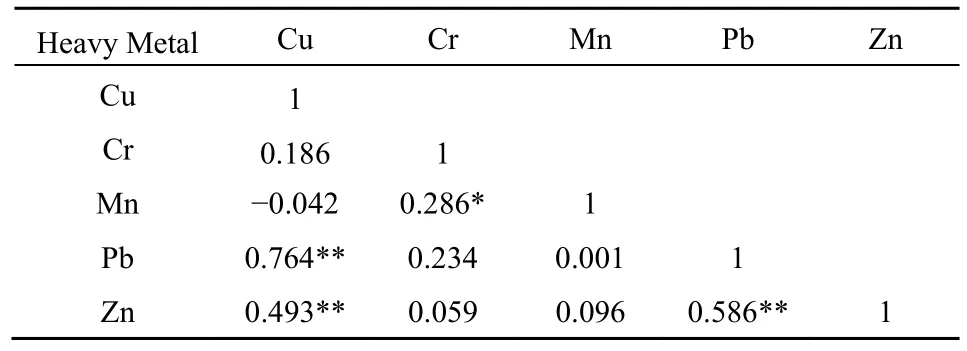
表2 土壤重金属含量相关系数矩阵Table 2 Soil heavy metal content correlation matrix

表1 工业区土壤重金属含量的描述性统计分析Table 1 Descriptive statistical analysis of soil heavy metal content mg·kg-1

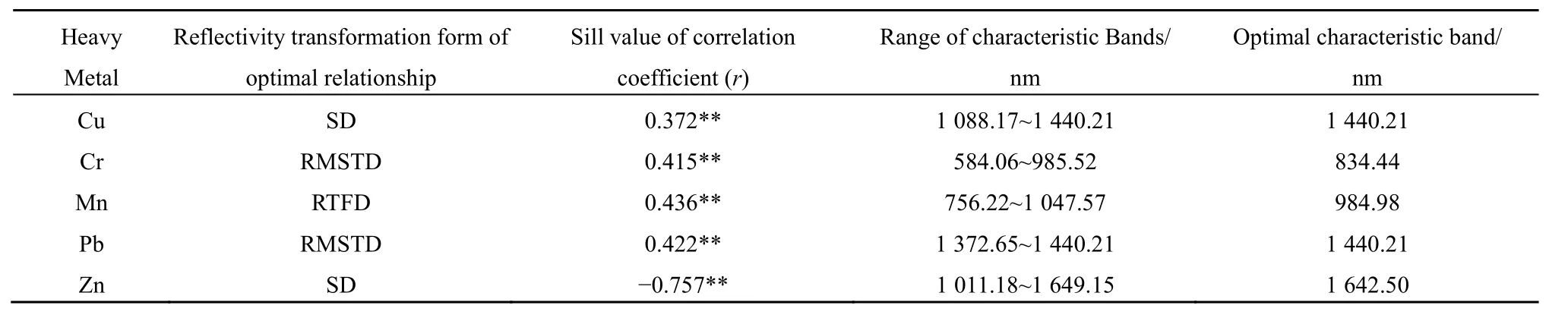
表3 不同重金属与反射光谱相关波段分析结果Table 3 Results of analysis of bands associated with different heavy metals and reflectance spectra

2.4 重金属含量反演预测模型比较

随机选取 51个样本作为建模样本用于模型建立，12个样本作为验证样本用于模型精度检验。将土壤光谱数据的8种变换形式与重金属含量在0.01水平上显著相关的波段（即特征波段）作为自变量，5种重金属含量作为因变量，分别采用偏最小二乘回归模型（PLSR）以及多元逐步线性回归模型（SMLR）构建工业区重金属含量预测模型，分析建模效果，确定最优模型并利用验证样本进行检验，最优建模结果及其光谱变换形式如表4所示。

最优模型的选择要求检验所建模型的决定系数（Coefficient of Determination，R2）与均方根误差（Root Mean Square Error，RMSE）的大小（夏芳等，2015；徐良骥等，2017）。决定系数R2反映模型的建模精度与稳定性，一般认为R2＜0.5，模型无法对所求变量进行预测；0.5≤R2＜0.65时，模型具备初步预测能力；0.65≤R2＜0.81时，模型具备较好的预测能力；R2≥0.81时，模型预测能力良好（Vohland et al.，2011）。均方根误差则检验模型对样本的拟合度，在对同种重金属的不同预测模型进行检验时，误差越低越好（程先锋等，2017）。由表4可知，每种重金属的最优预测模型所选用的数据变换形式不同。土壤Cu、Pb、Zn偏最小二乘回归最优模型选用二阶变换，土壤 Cr选用方根二阶变换，土壤Mn选用倒数二阶变换。多元逐步线性回归模型中，土壤Cu、Mn最优模型选用方根二阶变换，土壤Cr、Pb选用倒数一阶变换，土壤Zn选用倒数对数二阶变换。从建模效果来看，PLSR建模与验证的决定系数R2除Zn外均低于0.5，建模精度较低，不具备预测变量的能力。而SMLR建模的R2均达到0.65以上，其中Zn的R2达到0.974，均具备较好的预测能力；验证的R2除Mn外其他均达到0.5以上。与PLSR建模精度相比，SMLR建模精度与验证精度均明显提高，RMSE均有所下降，说明SMLR预测模型反演预测效果更好，对样本的拟合度更高，更具有稳定性与可靠性。一般地，数据低阶微分变换形式能够提高反演精度，但多数研究仅采用一阶微分、二阶微分形式，而较少利用其他变换形式的低阶微分形式进行模型反演（于庆等，2018；贺军亮等，2015；龚绍琦等，2010）。本研究所建的5种重金属的最优反演模型中，精度最高的模型所使用的数据变换形式分别是方根二阶变换、倒数一阶变换、倒数对数二阶变换，说明使用其他变换形式的低阶微分能够获得比原数据的低阶微分更高的模型精度，这可为今后的数据处理研究特别是工业区等受人为活动强烈影响区域的反演研究提供参考。

3 结论

（1）经统计，上海闵行区西南部工业区土壤重金属Cu、Cr、Mn、Pb、Zn存在明显积累，含量平均值依次为29.38、106.32、583.14、34.13、111.15 mg·kg-1，且表现为复合污染或具有同源性。空间分布上，土壤Pb、Cu、Zn空间分异较大，变异系数分别为 0.86、0.6和 0.55，受到工业生产等强烈人为活动因素干扰；土壤Cr、Mn空间分异小，受外界干扰小。

（2）经降噪处理后工业区土壤光谱反射曲线整体走势一致，呈缓斜型，反射率在10.01%～50.20%之间。除特定谱段受铁氧化物（409.55 nm）、有机质（825～900 nm)、水（1400～1425 nm）的影响存在光谱曲线吸收带外，光谱反射曲线走势均随波长增加而上升。

（3）土壤重金属含量与不同光谱变换数据相关性分析结果表明，土壤Cu最优特征波段为1440.21 nm；土壤Cr为834.44 nm；土壤Mn为984.98 nm；土壤Pb为1440.21 nm；土壤Zn为1642.50 nm。最优特征波段均在近红外波段范围内。

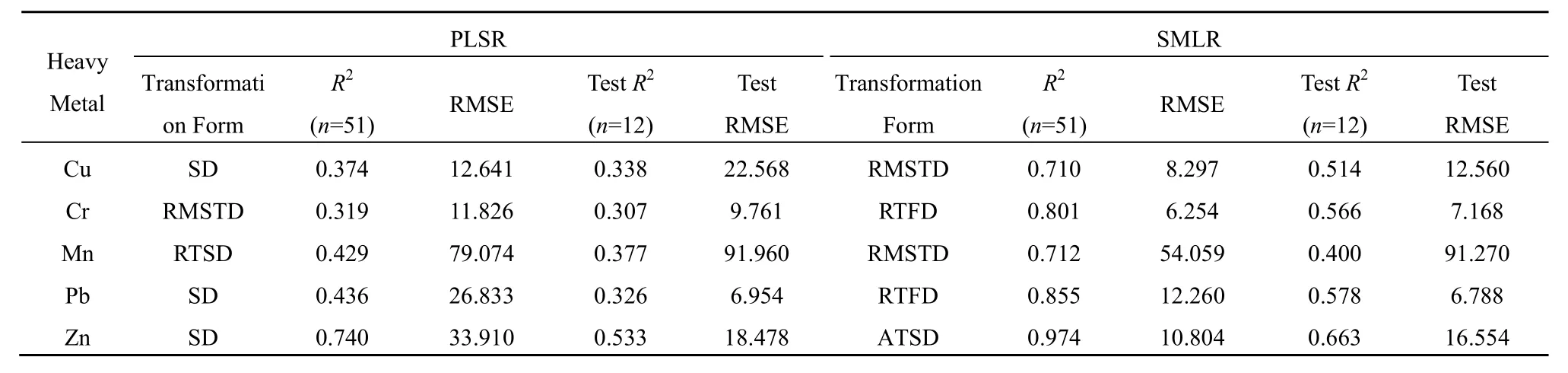
表4 工业区土壤光谱反射率预测重金属含量模型建模及验证精度比较Table 4 Prediction of spectral reflectance of soil in industrial area comparison of modeling and verification accuracy of heavy metal content model

（4）与PLSR建模精度相比，SMLR建模的R2均达到0.65以上，其中Zn的R2达到0.974；验证的R2除Mn外其他均达到0.5以上。SMLR的建模效果优于PLSR，各项系数检验说明SMLR反演预测效果更好，对样本的拟合度更高，更具有稳定性与可靠性，所建模型基本能满足工业区土壤重金属含量反演预测需求。