井下导线测量及陀螺定向测量的精度分析探讨

张 洁

(大同煤矿集团 马道头煤业有限责任公司，山西 大同 037100)

煤矿井下巷道开拓前，需要进行必要的导线测量工作来规划指导井下巷道的现场施工，以期满足设计图纸的精度要求。在进行井下导线测量时，必然有可能产生各种误差，因此有必要对产生的各种误差进行分析、总结以及了解误差累计的规律，进而采取有效的措施来减小甚至消除这种误差，从而为矿井井下开拓工程奠定坚实的基础。

1 导线测量误差分析

采用导线测量控制井下开拓巷道的掘进精度时，需要对导线的水平角、竖直角和边长三要素进行综合测量。根据以往经验和文献研究可知，实际导线测量工作中边长和竖直角的测量一般均能满足测量的精度要求，因此着重对水平角测量精度进行分析研究。

水平角测量的精度误差主要由测量仪器本身的误差、测量方法的误差以及对中误差所致。其中：

（1）测量仪器本身的误差诱因有多方面，例如仪器零件的加工误差、组装和校核误差、仪器结构误差和稳定性等因素。

（2）测量方法的误差主要是由于人为的原因造成的，其误差值大小如式(1)所示。

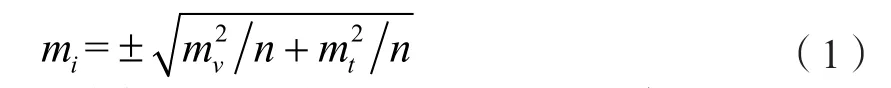
式中构成测量方法误差的核心因素主要由照准误差mv、读数误差mt和测回数n组成。

（3）对中误差由全站仪和其前后的棱镜对中线测量误差所致，进一步导致水平角的测量误差。

2 导线测量误差计算

水平角测量精度可以通过测角中误差这一数值指标来反馈，而测角中误差又可以根据多个双次观测值的方法求出。假设每次测量结果等精度，则可以利用两次观测值的差值来计算测角中误差，如式（2）所示。

式中：d为两次同精度测量结果的差值，n为两次测量导线上差值的个数，且差值尽量在不同的导线上选取，并且尽量使差值的数量最大化。

为了提高测量结果的可靠性，可以选取多组导线进行双次观测值的计算，并取多个双次观测值结果进行平均，计算公式如式（3）所示。

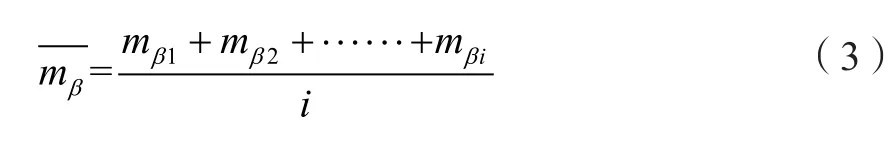
式中：mβi为第i次双次观测值结果，i值越大则测角中误差值的计算结果越精确。

以山西马道头矿为例，由于该矿井回风大巷关键线路施工段现场施工时进行了多次重复测量，构成了可以采取双次观测值的方法来计算测角中误差的前提条件。采用双次观测值测量方法时，在两条相互独立的导线上分别选取了8组点进行差值计算，其差值变化情况以及测角中误差计算结果如图1所示。从图中可以看出，除了第7组测点的差值和相应的测角中误差值波动性比较大以外，其余测点的差值和相应的中误差值变化波动性均较小，其测角中误差平均值为5.2″，满足安全规程要求的测角中误差小于7″的规定，但是比较接近规定的临近值大小，说明测量结果精度较低，虽然能够满足测量要求，但测量结果对工程质量的精度控制度不高。

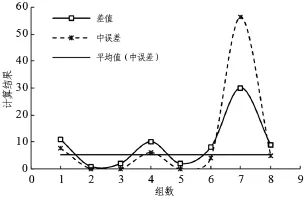
图1 双次观测值法测量结果分析

3 陀螺定向测量精度分析

陀螺仪本身为一种具有测定真北方位的精密仪器，将其与经纬仪组合形成的陀螺经纬仪能够不受时间和环境的限制，并且具有操作简单、测量效率高等优点，因此在矿山井下测量中采用陀螺经纬仪能够有效地提高测量的效率和测量的精度。

根据白塞尔公式计算陀螺经纬仪一次测定的测角中误差计算公式如式（4）所示。

式中：

v-1次测回的数值，为了确保测量计算结果的精确性，一般进行5次测回取平均值。

同样以该矿井回风大巷关键线路施工测量为背景，采用首级±15″的陀螺经纬仪进行测定，共进行5次测回，每次测回分为左右两侧各一次，并对5次测回结果取平均值，测定结果如图2所示。从图中可知，5次测量值根据公式（4）计算的测角中误差的平均值为2.74″，远远满足首级±15″的精度要求，且测角中误差值远远小于采取导线测量的结果，几乎是采用导线测量方法测定结果的一半，这说明采用陀螺经纬仪定向测量能够有效地提高测量的精度，进而更好地对现场工程质量的精度进行控制。

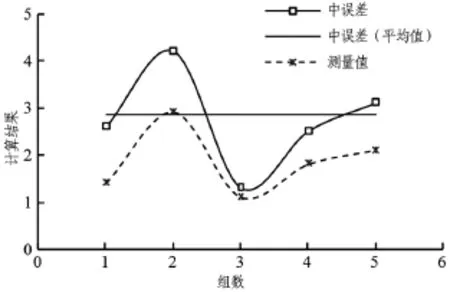
图2 陀螺定向测量结果分析

4 结论

传统的井下导线测量虽然能够满足安全规定的测量精度，但其测量精度较低，且误差主要来源于水平角测量误差。由于水平角测量精度可以通过测角中误差这一数值指标来反馈，因此对山西马道头矿回风大巷关键线路采用导线测量和陀螺定向测量计算结果进行对比，可知导线测量的测角中误差为5.2″，而采用陀螺经纬仪测量的测角中误差为2.74″，测角中误差几乎为导线测量结果的一半，说明采用陀螺定向测量能够有效地提高测量的精度，对矿井重要巷道的施工开拓有重要的规划指导意义。