偏心电磁力对永磁同步电主轴转子可靠性的影响
李嘉明,于慎波,赵海宁,夏鹏澎
(沈阳工业大学 机械工程学院,沈阳 110870)
0 引言
永磁同步电主轴是高档数控机床关键部件之一,在机床加工中发挥着重要作用。电主轴运转过程中,由于质量不平衡、转子变形、定转子的制造公差、轴承公差及不平衡质量等原因不可避免地造成了转子和定子之间的静、动偏心,该偏心又产生了不平衡磁拉力[1]。通过对电主轴内部最易损坏的部分进行寿命估计从而得出整个电主轴的使用寿命,可以提高数控机床加工的可靠度。电主轴的工作状态直接决定机床加工精度,因此对转子的疲劳强度分析对实际生产有重要意义。
纵观国内外文献,很多学者都对永磁同步电机气隙磁场进行了研究。王凤翔提出应用电磁场、应力场与温度场耦合方法,分析计算电机定转子的高频和高速损耗和温升分布,电机的强度刚度、振动和噪声的方法[2]。 将转子受力状况简化为平面应变问题,在此基础上推导出了两层过盈配合、三层过盈配合转子的应力场、应变场、位移场的解析公式[3]。Ronghai Qu等通过改进永磁电机的设计参数,从而减小了径向电磁力并提高了转矩密度和效率[4]。但在永磁同步电主轴转子偏心磁场分布以及偏心引起的电磁力对转子机械强度和疲劳寿命的影响方面都没有太多的研究。
本文针对转子偏心状态下,进行了永磁同步电主轴转子气隙磁场的理论计算,并与有限元仿真结果进行比较,吻合较好。不平衡磁拉力对转子机械强度和疲劳寿命有一定影响。
1 电机气隙磁场分布
本文分析了在空载下电主轴内部气隙磁场分布。空载下电主轴气隙内部磁场分为径向磁密和切向磁密,均由永磁体产生。其中产生不平衡磁拉力的主要原因为径向磁密,由于切向磁密成分较小,通常忽略其影响。在不考虑定子开槽影响的情况下,气隙内磁场分布呈较为规则的矩形分布规律,当考虑定子开槽的影响时,气隙在有槽处的磁导率发生变化,径向磁密分布也发生变化。本次样机为4极18槽永磁同步电主轴,电主轴参数如表1所示。

表1 永磁同步电主轴基本参数
由文献[5]可知,永磁同步电主轴气隙磁场分布为:

(1)

(2)
其中,r为气隙处半径,μ0为真空磁导率,μr为相对磁导率,Rs为定子内径,Rr为转子外径,Rm为永磁体外径,α为转子位置角。
定子槽通过减少每极的总磁密来影响磁场,通常引入卡特系数对其进行解释[6],考虑定子开槽影响后,气隙磁导率产生周期性变化。未开槽处气隙磁导率为:
(3)
开槽后,气隙相对磁导率变为:
(4)
由此得出开槽后气隙径向磁密为:
(5)
分别对气隙径向磁密进行解析法计算和实验仿真,其结果如图2所示。由分析结果可知理论计算值与有限元仿真结果吻合。

图1 有限元仿真界面
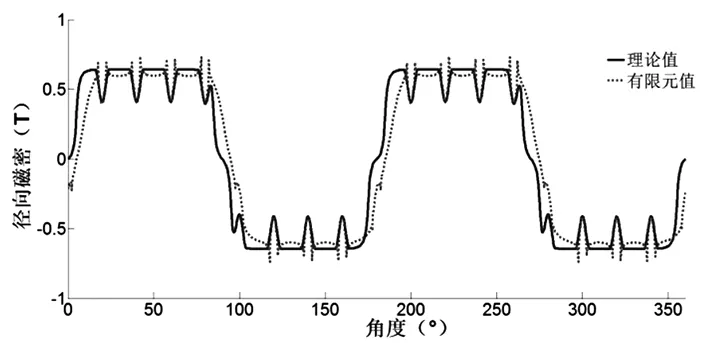
(a)气隙径向磁密
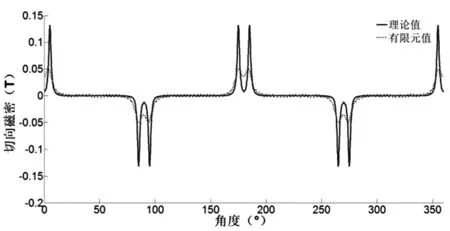
(b)气隙切向磁密图2 气隙磁密
2 不平衡电磁力的计算
2.1 转子偏心理论
永磁同步电主轴转子偏心主要分为动偏心和静偏心。静偏心时转子中心为旋转中心,但不与定子中心重合;动偏心时转子旋转中心不与定转子中心重合。转子偏心的存在会使气隙大小发生变化,因而产生作用在转子上的不平衡磁拉力。不平衡磁拉力的计算既与时间有关又与定、转子位置有关[7]。

图3 转子偏心示意图
图中Os为定子几何中心,Or为转子几何中心,O为转子旋转中心,Rs为定子半径,Rr为转子半径,r0为初始状态下转子中心距定子中心距离,r为旋转后某一时刻t转子旋转轨迹半径。根据几何关系可得:
(6)
(7)
则在t时刻、位置α处气隙大小为:

(8)
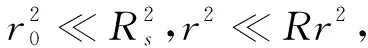
当r=0时,转子偏心为静偏心;当r≠0时,转子偏心为动偏心。
正常状态下的转子磁密是对称分布的,当存在偏心时,气隙减小位置磁密会增大[8]。实验证明转子偏心会影响径向和切向磁密,这同样会引起不平衡磁拉力[9]。将磁密分解为径向磁密Br和切向磁密Bt,则可以得到径向和切向电磁力密度表达式:
(9)
(10)
则径向、切向电磁力为:
(11)
(12)
弯曲偏心常出现在转子为细长结构的电机中,这会使得轴向偏心程度不同,在转子中部偏心最大[10]。径向电磁力会随着挠度的产生而发生变化。

图4 转子不平衡磁拉力空间示意图
径向电磁力作用在转子上产生挠度,其可被分解为轴向和径向两个分量,轴向力分量抵消,径向分量产生新的不平衡磁拉力,挠度的存在使得沿轴向气隙大小也发生不均匀分布,将轴弯曲拟和成二次曲线:
L(z)=c1z2+c2z+c0
(13)
轴向气隙大小为:
(14)
考虑轴挠度后的不平衡磁拉力公式为:
(15)
2.2 不平衡磁拉力的计算
分别选取偏心量0.1~0.3mm进行偏心电磁力密度计算,并将不同偏心值的气隙径向磁密分布和径向电磁力值进行比较,得到图5、图6所示结果。
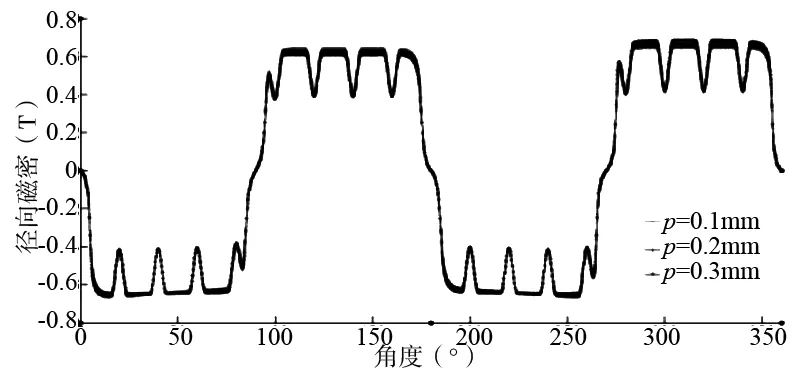
图5 不同偏心量气隙磁密

图6 不同偏心值产生的径向偏心力
图7是沿圆周方向,偏心后的气隙电磁力密度值,随着偏心量的增加,沿偏心方向的径向电磁力密度逐渐增大,径向电磁力密度不对称分布程度加剧,从而不平衡磁拉力增大。

图7 不同静偏心值下电磁力密度沿圆周分布
3 偏心对转子强度影响
3.1 转子机械强度分析
由于永磁电机的高效率和高功率密度,永磁转子成为中小功率高速电机的首选结构[11]。通过有限元分析软件对永磁同步电主轴转子轴进行强度分析,以偏心最大值0.3mm为例,首先将轴模型导入有限元分析模块中并赋予模型材料SAE 1045-450-QT,对模型施加约束、载荷,得到转子轴的应力云图,最大应力为134.35MPa,小于屈服强度355MPa,满足机械强度要求。由分析结果得出:轴未发生强度破坏。但是在轴输出端轴肩处存在应力集中,是潜在的发生强度破坏的危险截面,可以通过对轴进行结构改进以减少应力集中,提高可靠度。
3.2 增加轴强度措施
为了散热,轴内部设计为中空结构,本文通过改善轴内部孔结构分布,来增加危险截面的机械强度,达到消除危险界面的应力集中的效果。同时,在轴肩应力集中部位处采取导内圆角措施,减少应力集中,改进方法如图8~图10所示。

(a) 改进前

(b)改进后图8 轴内部结构图

图9 轴肩处导内圆角
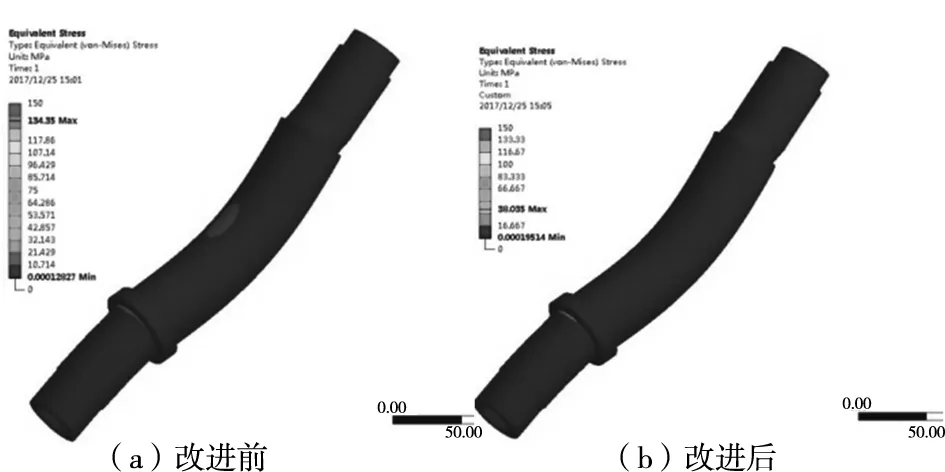
图10 改进前后轴应力云图比较
改进后轴的最大应力减小到38.05MPa,轴强度得到提高,降低了因应力集中而产生断裂的可能性,提高了可靠度。同时,通过仿真结果可以看出:相比只考虑离心力作用,考虑不平衡磁拉力后所计算出的最大应力,更接近实际情况,实现了更准确的机械强度校核。
4 偏心对转子疲劳寿命的影响
本样机转轴疲劳类型为高轴疲劳,通过有限元仿真对转轴进行疲劳分析。采用Goodman曲线对得到的各个离散的载荷块修正,考虑平均应力的影响,得到等效的应力幅[12]。有限元仿真载荷谱及修正曲线如图11所示。

图11 疲劳寿命仿真界面
通过有限元仿真得到不同偏心量的疲劳寿命见表2。

表2 不同偏心值疲劳寿命
通过有限元仿真结果可以看出,转子疲劳寿命缩减速度随着转子偏心量增加而加快。相比较只考虑质量偏心的计算方法,考虑不平衡磁拉力作用后的疲劳寿命计算方法更加准确,实验计算结果更具真实性和可靠性。
5 结论
本文对永磁同步电主轴气隙磁场进行了理论计算,并与有限元仿真进行比较,吻合较好。在原有气隙磁场计算方法基础上加入转子偏心理论,得出了永磁同步电主轴在不同偏心量下的气隙磁场分布情况,与有限元仿真结果吻合,验证了永磁同步电主轴偏心气隙磁场计算方法的正确性。
不平衡质量产生的离心力和磁场畸变引起的不平衡磁拉力会随着偏心量增加而增大,偏心量达到最大时,永磁同步电主轴转子强度满足机械强度要求。永磁同步电主轴内部孔结构改进和轴肩处内导圆方法达到了减小应力集中、增加了转子的可靠性目的,通过两种改进方法使转子强度提高4%。与只考虑偏心质量产生的离心力相比,加入不平衡磁拉力对转子机械强度和疲劳寿命的计算方法更具严谨性与可信性,对于电机内部关键部件机械特性研究有重要意义。

