轴承滚子尺寸误差与径向跳动的Copula建模与分析

魏建波，薛玉君,,，余永健，李济顺，庞碧涛

(1. 河南科技大学 a.机电工程学院；b.河南省机械设计及传动系统重点实验室，河南 洛阳 471003；2. 航空精密轴承国家重点实验室，河南 洛阳 471039)

0 引言

滚动轴承作为机械传动系统中的一种重要基础零部件，其旋转精度是影响整个轴系运转的重要因素。轴承零件的加工精度是影响滚动轴承旋转精度的重要因素，因此轴承零件的尺寸误差对轴承的旋转精度有着重要影响。

近年来众多学者在轴承旋转精度方面进行了深入研究：宋飞和史文祥[1-2]在已知圆柱滚子轴承套圈滚道误差的条件下，通过仿真得到其径向跳动变化曲线，并分析了外圈径向跳动与外圈滚道圆度误差谐波阶数、谐波系数的关系。史文祥[3]运用编程仿真和数理统计的方法预测圆柱滚子轴承的旋转精度。在外圈仅存在圆度误差、轴承零件为刚性等假设条件下运用C++编程实现其预测仿真算法。建立了圆柱滚子轴承外圈径向跳动的统计学模型，分析了圆度误差的分布特征与其谐波的分布特征。武全有[4]建立载荷约束下滚子直径尺寸误差与轴承运动精度关系的数学模型，对圆柱滚子轴承的运动状态进行数值仿真，研究载荷约束下滚子尺寸误差对轴承运动精度的影响，得到了以下结论：随着轴承径向载荷的增大，内圈径向跳动量呈逐渐减小的趋势，且逐渐趋于平缓；多个滚子存在误差时，内圈径向跳动量大小与滚子的排布方式有关。留剑等[5]建立角接触球轴承旋转精度的五自由度拟静力学模型，分析了轴承元件接触面波纹度对球轴承运动精度的影响规律。吴柏华等[6]和李传顺等[7]从深沟球轴承内部几何关系入手，考虑了滚动体的直径误差、内外圈滚道的圆度误差等，着重分析了滚动体的直径误差以及内外圈滚道圆度误差对深沟球轴承非重复性跳动的影响规律。宋飞[8]和王宝坤[9]在考虑轴承内圈转动的情况下，讨论了滚子直径误差对轴承径向跳动的影响。另外，李传顺等[10]研究了多方面因素对深沟球轴承旋转精度的影响。武全有等[11-12]根据轴承元件间的几何运动关系及载荷接触变形关系，建立了载荷和轴承元件几何尺寸误差共同作用下轴承的回转精度几何模型，分析了在载荷和几何约束共同作用下轴承运动精度的变化规律。纪鹏[13]对在载荷条件下滚子直径误差对轴承性能的影响进行了分析。马方波[14]根据Houpert推导的计算公式，建立了滚子、滚道点接触法向载荷和轴心轨迹的计算模型，理论验证了单个滚子存在直径误差与多个滚子存在直径误差对球面滚子轴心轨迹的影响。崔伶俐[15]等对滚动轴承外圈故障的振动响应进行了定量地分析，建立了滚动轴承非线性振动的故障性评估模型，给出了振动响应与误差尺寸的对应关系，获取了不同故障级别下的响应特征。Guanci Chen等[16-17]将圆柱滚子轴承作为研究对象，考虑了滚动体直径对轴承载荷分布的影响，并对轴承滚道圆度和滚动体大小对轴承运行情况进行研究。Copula函数能够有效地描述特征变量间的相互关系，因此被广泛应用于水文、金融等各项领域中。但是，目前大多数针对滚子尺寸误差与径向跳动的相关结构描述的研究中，利用Copula函数作为研究模型，还少见报道。

为此，本文以圆柱滚子轴承为研究对象，针对滚子尺寸误差及轴承径跳动的相关性分析问题，提出了建立轴承滚子尺寸误差和轴承径向跳动二维Copula函数模型的方法及模型合理性的验证方法。基于建立的Copula函数模型对两者的相关性进行了分析。为系统分析滚子尺寸误差与轴承径向跳动的相关性提供了有效手段。

1 特征变量的统计分析

1.1 特征变量的获取

在本文中，以圆柱滚子轴承的滚子直径尺寸误差和轴承的径向跳动为特征变量。由大量实验数据统计分析得到滚子尺寸误差的分布符合正态分布，故可给定滚子尺寸误差的特征参数由正态随机数生成滚子尺寸误差数据。根据数理统计的知识：大于30个数据样本即具有统计学意义，所以本文在0.001～0.1mm之间产生两组长度为40的正态随机数作为滚子尺寸误差数据并分别标定为1号、2号滚子。以滚子直径尺寸误差作为输入变量，代入轴承径向跳动的计算方法，获得每种滚子尺寸误差组合下的轴承径向跳动数据。各特征变量的特征参数如表1所示。

表1 特征变量的边缘分布参数

1.2 特征变量的边缘分布函数与检验

要建立以轴承滚子尺寸误差和轴承径向跳动为特征变量的二维Copula联合分布函数，首先要确定特征变量各自的边缘分布函数。根据上文可知滚子的尺寸误差是正态随机数，而其对应的轴承径向跳动的分布还不确定，在此假定轴承径向跳动也是符合正态分布的，然后运用Kolmogorov-Smirnov检验法(以下简称K-S检验法)来验证假设分布的合理性。K-S检验结果如表2所示。

表2 Kolmogorov-Smirnov单样本检验中D的值

Kolmogorov-Smirnov单样本检验中D的判断依据是当D的值大于D(n，α)，则拒绝原假设，反之则接受。在置信水平为α=0.05时，三个特征变量的D值均小于D(40,0.05)=0.215[18]。且伴随概率P也均大于0.05，所以不能拒绝原假设，故三个特征变量的数据均符合正态分布。

根据K-S检验分析可知，轴承1号、2号滚子的直径尺寸误差和轴承径向跳动的数据分布是符合正态分布的。

2 Copula函数参数估计与模型优选

要选择最合适的Copula函数，首先要确定不同Copula函数的建模参数，本文用半参数估计法分别估计高斯Copula、t-Copula函数、Gumbel-Copula函数、Clayton-Copula函数、Frank-Copula函数等5种Copula函数的建模参数值。

根据计算得到的Copula函数建模参数可以分别建立相应滚子误差和轴承径向跳动的函数模型。本文选择均方根误差法[16]分别对5种函数模型进行拟合优度评价。结果如表3所示。

表31号滚子直径误差w1与轴承径向跳动s各建模模型的拟合优度评价

均方根误差高斯Copulat-CopulaGumbelClaytonFrankRMES0.02980.02390.02340.03520.0271

表42号滚子直径误差w2与轴承径向跳动s各建模模型的拟合优度评价

均方根误差高斯Copulat-CopulaGumbelClaytonFrankRMES0.03220.03500.02800.04170.0321

依据Copula模型选择方法均方根误差法的原则，误差值越小的模型为优选的模型。据此拟合优度的评价标准，综合上述两个均方根误差表3、表4的结果可知，1号和2号滚子直径误差与轴承径向跳动的Copula函数模型中都是Gumbel-Copula函数对应的均方根误差最小，所以选用Gumbel-Copula函数来描述特征变量间的相关结构。

3 Copula函数模型建立与验证

3.1 二维Copula函数的联合分布函数模型建立

根据Sklar定理可知，要建立二维联合Copula函数分布模型，要知道连接特征变量的连接函数和各自的边缘分布。根据之前的分析结果可知，滚子直径误差和轴承径向跳动的连接函数为Gumbel-Copula函数，二元Gumbel-Copula函数的分布函数和概率密度函数公式为：

分布函数：

(1)

式中，u(w),v(s)分别为滚子直径尺寸误差w与轴承径向跳动s的边缘分布,θ为Gumbel-Copula函数的建模参数。

为简化方程形式，令W=(-lnu(w))θ+(-lnv(s))θ，则概率密度函数：

(2)

3.2 模型的合理性验证

滚子直径误差与轴承径向跳动的所建立的联合分布模型是否合理，通过比较特征变量数据点所对应的经验累积概率值和理论累积概率值的一致性来验证。理论累积概率值可以经过建立的模型函数求解，经验累积概率值由下式计算得到：

(3)

其中，N为随即变量的样本总数，nmk为样本值(xm,yk)出现的频数。

根据计算的结果绘制以理论累计概率Fthe为横坐标，经验累积概率值Femp为纵坐标的散点图。从图1和图2中可以看到各个相关变量所对应的理论值和经验值基本都在一条直线上，并且两者的线性相关系数R分别为0.982和0.981，说明滚子尺寸误差和轴承径向跳动的联合分布函数模型与实际情况的拟合效果良好。

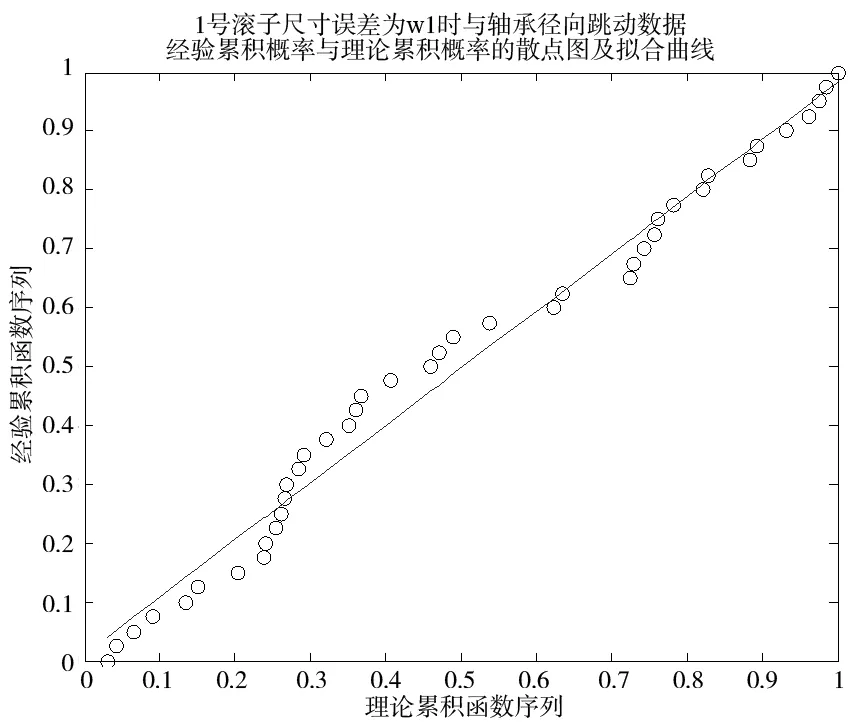
图1 1号滚子尺寸误差下Copula函数模型验证

图2 2号滚子尺寸误差下Copula函数模型验证

上述情况已经讨论了两个相邻滚子存在尺寸误差时，轴承滚子的尺寸误差数据与轴承径向跳动的Copula函数建模问题，另外两种分布情况：①两个存在尺寸误差的滚子相间排布，即1号滚子尺寸误差保持不变，3号滚子尺寸误差和上述2号滚子尺寸误差一致。②当所有滚子存在相同尺寸误差w1时。

根据上文同样的建模步骤和方法分别求出对应的径向跳动值，然后进行Copula函数模型建立。

4 特征变量间的相关性分析

Copula函数在描述特征变量间的相关结构较传统的分析手段有着明显的优点，能够轻松便捷地解决传统分析方法中的遇到的难题。本节将会针对圆柱滚子轴承滚子直径尺寸误差和轴承径向跳动之间的非线性相关关系进行分析和讨论。

相关系数是度量随机变量之间相依性的常用指标。分别采用Pearson线性相关系数γn、Spearman秩相关系数ρn和Kendall系数τ来表征，秩相关系数反应的是变量间的单调相依性，其在非线性单调变换下保持不变，具有良好的统计特性。对于本文选取基于样本数据的Kendall系数τ、基于构建的Copula函数的Kendall系数和Spearman秩相关系数ρn和来表征变量间的相关性。

表5 1,2号滚子存在误差时特征变量间的秩相关系数τ

表6 1,3号滚子存在误差时特征变量间的秩相关系数τ

由表1可知，两滚子尺寸误差的均值基本相等，方差第二个滚子较小。结合表5、表6分析可知：滚子直径尺寸误差与轴承径向跳动是显著相关的。当两个存在误差的滚子相邻排布时，滚子的直径尺寸误差与轴承径向跳动的秩相关系数差别较大，分别为0.5117和0.6373。说明其对轴承径向跳动的影响是略有不同的，方差较小的滚子误差数据分布较为集中，其与轴承径向跳动相关系数较大。当两个存在误差的滚子间隔一个无误差的滚子排布时，两个存在误差的滚子的直径尺寸误差与轴承径向跳动的秩相关系数有微小差别，但整体上相差不大，分别为0.5774和0.5618。说明其对轴承径向跳动的影响是大致相同的，两者对轴承径向跳动的贡献是相同的，地位是对称的。

所有滚子存在同一尺寸误差时，特征变量尺寸误差与轴承径向跳动的秩相关系数如表7所示。

表7 所有滚子存在相同误差时特征变量间的秩相关系数τ

根据表7可知，当各个滚子尺寸误差均为w1时，轴承径向跳动的量值明显减小。但滚子尺寸误差与轴承径向跳动的秩相关系数为0.8700，与相邻两个滚子存在直径尺寸误差时相比，秩相关系数的值显著增大。综上所述可以得出：滚子尺寸误差的一致性对轴承径向跳动具有显著影响。

综合分析误差滚子不同排布下滚子尺寸误差与轴承径向跳动的相关系数可得：滚子误差的排布方式和尺寸误差数据的边缘分布数字特征是综合影响滚子直径尺寸误差与轴承径向跳动的秩相关系数的因素。

5 结论

通过统计学、运动学及仿真和理论验证相结合的方法，建立了滚子尺寸误差及轴承径向跳动的Copula函数模型，对圆柱滚子轴承滚子尺寸误差及轴承径向跳动的相依性进行了系统的分析。得出以下结论：

(1)基于本文的数据，对于圆柱滚子轴承，相邻两个滚子存在尺寸误差时，经过模型合理性验证得到：滚子尺寸误差数据与轴承径向跳动的最优Copula函数模型为Gumbel-Copula函数。

(2)滚子直径尺寸误差与轴承径向跳动是显著相关的。且两个滚子存在误差时，滚子尺寸误差分布方差越小即集中，滚子的直径尺寸误差与轴承径向跳动的秩相关系数越大。所有滚子存在相同误差时，两者的相关系数较两个滚子存在尺寸误差时显著增大。综合得出滚子误差的排布方式和尺寸误差数据的边缘分布数字特征是综合影响滚子直径尺寸误差与轴承径向跳动的秩相关系数的因素。

(3)通过对比分析不同排布方式下的模型可得：滚子误差的不同排布方式会影响优选的Copula函数。误差滚子数量相同、排布方式不同时，滚子尺寸误差与轴承径向跳动的优选Copula函数相同。当所有滚子存在相同尺寸误差时，优选的Copula函数为t-Copula函数。该方法能正确分析轴承径向跳动与滚子尺寸误差的相关性，具有一定的工程应用价值。