基于Maxwell滑动模型的压电驱动器非对称迟滞特性研究*
王行刚,杨雪锋
(1.常州机电职业技术学院,江苏 常州 213164;2.中国矿业大学 机电工程学院,江苏 徐州 221008)
0 引言
随着精密工程和微细工程的迅速发展,亚微米和纳米级定位技术和微动伺服技术已成为微机电系统、超精密加工、微电子、光电子和生物工程等前沿学科的关键技术。压电陶瓷驱动系统作为理想的纳米微位移元件,具有体积小、位移分辨率高、频响高、承载力大、无噪声、不发热等特点,获得了广泛应用。但是在实际应用过程中,其本身的一些非线性因素给精密定位带来一定的影响,而其中迟滞特性是影响精度的最主要的因素[1]。
为了减小压电驱动器的非线性迟滞现象给定位精度带来的负面影响,国内外学者对此进行了深入研究。Newcomb C V[2]提出用电荷驱动代替经典的电压驱动,但电荷控制法需要专用的控制电荷放大设备,并且在控制过程中需要精密的电荷测量元件,以补偿电荷泄漏造成的控制误差。P Ge和Song D等提出Preisach模型的分布函数在输入上升及下降过程中具有不同的转换值,其值为+1或者是-1,从而产生迟滞控制项[3-4]。参考文献[5]则提出了神经网络动态迟滞模型等。这些方法虽然在一定程度上减小了非线性和迟滞特性的影响,但是都对压电驱动器的特性进行了某种简化甚至不考虑其物理意义,并且算法复杂,实时性不好,影响其在实际控制过程中的使用。
M Goldfarb等[6]则以Maxwell滑动模型为基础建立迟滞模型,利用简单的机械元件来描述非线性对称迟滞系统。Maxwell滑动模型具有参数少[7],结构简单的优点,但是存在弹性滑块单元的参数耦合问题,所以只能用来描述对称迟滞曲线,但是压电陶瓷驱动器本身的非对称迟滞现象,Maxwell滑动模型所得到的误差较大,不能用于实际控制系统。本研究主要对传统的Maxwell滑动模型进行改进,将其并联结构修改为串并联结构,推导出新的数学表达式,然后利用递推线性回归法实时求解改进型Maxwell滑动模型的参数值,使其能够满足对压电陶瓷的非对称迟滞现象进行描述,并用于实际控制系统。
1 压电驱动器Maxwell滑动模型的建立
1.1 经典Maxwell滑动模型
经典Maxwell滑动模型以简单的机械元件来描述非线性迟滞系统,如图1a所示。这个模型利用弹簧和滑块组成,根据外力和时间的关系来建立迟滞非线性关系。其中每个单元均由一个无质量受库仑摩擦的滑块和一根线性弹簧组成。在t时刻,对第i个弹簧滑块单元来说,摩擦力fi与其当前位移xi(t)的关系如式(1)所示:
(1)
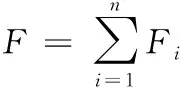
式中,ki为弹簧的刚度系数,Δi为弹簧的最大形变量,δi为弹簧当前形变量。F为整个系统的输入力,x为对应的位移[8-9]。
当弹簧力大于库仑摩擦力的时候,滑块开始移动,进入滑动区。即施加的外力只需要克服库仑摩擦力,而位移增加并不能使弹簧的伸长量增加,使得阻力增加。

(a)滑动模型结构 (b)输出曲线图1 经典Maxwell模型的结构与输出曲线图
当只有一个Maxwell模型时,模型的输出为一个斜方形,而不是一个平滑的曲线。若为8个模型并联,则输出为图1b所示。式(1)中,xi(t+1)=xi(t)-Δisgn(δi)针对滑块进入滑动区时,根据弹簧形变量,随时修正x的值,即弹簧的形变量达到最大时,滑块立刻由使得滑块可由滑动区进入线性区。
1.2 Maxwell滑动模型的改进
在传统的Maxwell模型中,虽然可以根据弹簧形变量的方向来修正整个系统的输出,但是无论如何,根据公式(1)和公式(2)所绘制的曲线必然存在对称性[x],而压电驱动器的迟滞曲线和传统的Maxwell模型描述的为曲线正好相反[xx],压电驱动器的位移随电压升高而增加,为下凹曲线,随电压降低而减小,为上凸曲线。因此若使用此模型来预测实际的压电陶瓷驱动器,则会产生较大的误差。
本研究将对上述的Maxwell模型作以下改进:
① 针对实际的压电驱动器的响应曲线一般为非对称性的特点,本研究将此模型分为两组,依据弹簧形变量的方向,选择启动其中一组Maxwell弹簧滑块单元。
② 通过借鉴神经网络给输入信号分配权重的方法,给每个弹簧滑块单元分配不同的权重wi,当Δisgn(δi)>0的时候,才会启动这个弹簧滑块单元。通过适当安排权重参数wi,使得每个弹簧滑块单元的输出力依次对输入力F产生影响,达到修正Maxwell滑动模型的目的,使其可以模拟压电驱动器的非对称型迟滞曲线。
公式(2)表示一个弹簧滑块单元输入力与输出位移的方程,整个系统的数学表达式如公式(3)所示。

(2)

(3)

(a) 改进型Maxwell滑动模型 (b)改进型Maxwell滑动模型的输出曲线图2 改进型Maxwell的结构与迟滞曲线图
1.3 弹簧滑块单元有关参数的确定
经典的Maxwell滑动模型采用并联方式,在求取参数时会遇到参数耦合的问题。T J Yeh[10]用linear programming[11]方式,先算出最后一个弹簧滑块单元的参数,再由后往前代入下一个进行计算。
在改进型Maxwell滑动模型中,通过加入权重参数,将并联模型改为串联模式,有效消除了参数的耦合问题。即在整个模型的工作过程中,任一时刻只有一个弹簧滑块单元处于线性工作区,其余单元不是尚未启动就是已经进入滑动状态。这就使得求取弹簧滑块参数的问题变成一个如何求取权重和如何使用一个弹簧滑块单元来描述迟滞曲线某一区段的曲线拟合问题。
由于涉及到多变量输入及权重分配问题,为了简化建模过程,本文使用了神经网络逼近的方法来求取各个弹簧滑块单元的权重。这里采用8个弹簧滑块单元来模拟整个迟滞过程,其中4个用于上升过程,4个用于下降过程。则整个系统的输入为弹簧刚度系数k1~k8和输入力F,输出为整个系统的位移x,由此建立的BP神经网络拓扑结构如图3所示。该网络由输入层、输出层和两个隐层组成,其中两个隐层各有10个神经元,第一隐层采用S型传递函数,第二隐层和输出层采用线性传递函数。

图3 BP神经网络模型
由于在测量压电驱动器响应曲线的过程中存在干扰,我们将测量多组数据,在某一段响应曲线中找出一个弹簧滑块单元的k值,使得由此k值描述的直线与实验数据所形成的曲线误差最小。k值的求取能被描述为一个最佳曲线拟合的问题[11],可以采取如下计算方法。

(4)
其中,y(v)为压电驱动器的响应曲线,δ(t)为取样函数,xn为输入电压。设定初始状态下Ln=1,k1=0,令Fn+1=Yn,利用公式(4)就可以得到针对y(v)逐次修正的kn+1的值。
(5)
令ki=kn+1,将公式(4)代入公式(3)即可得到Maxwell模型的输出Fn,即压电驱动器的输出,如公式(3)所示。
但是应该使用几个弹簧滑块单元以及何时启动下一个弹簧滑块单元呢T J Yeh[10]采用将区间等分N段的做法,计算实测值和模拟值的误差来决定N的值。在这里我们使用一个阈值参数,当测量值与改进型Maxwell模型的输出值的误差大于阈值时,将增加一个弹簧滑块单元进入递归计算。

1.压电驱动器响应 2. 线性递归计算输出 3.误差曲线
图4说明改进型Maxwell滑动模型根据阈值参数增加一个新的弹簧滑块单元的情形。在图4中,实线为实际测量的压电驱动器的响应曲线,点状线是根据线性递推回归法计算出的参数值。压电驱动器在50V左右出现转折,误差超过设定阈值0.6,所以自动增加一个新的弹簧滑块元件进入计算。实际的阈值设定依据不同的压电驱动器和实验要求而设定,当压电驱动器的响应Yn与改进型Maxwell滑动模型的输出Fn的绝对误差大于阈值参数时,将计算结果kn、输入电压xn,压电驱动器的响应值Yn,分别代入改进型Maxwell滑动模型的ki、xi、fi,然后增加一个新的弹簧滑块单元进入计算,由此求出的kn+1。
2 模型的实验验证
本实验所用的压电驱动器为piezomechanics公司的PSt150/7/100 VS12直线型压电陶瓷驱动器,最大位移为100μm,位移测量元件为WNAD65型镍锰合金磁迹位置传感器,分辨率为0.1μm。
令阈值参数为0.6μm,使用线性递推回归法对采集到的压电驱动器的响应曲线Yn逐次迭代修正,计算出一个弹簧滑块单元参数,如表1所示。

表1 使用线性递推回归法计算得到的弹簧滑块单元参数值
对于表1,可以看出弹簧滑块单元1、2、3、4对应与迟滞曲线的上升阶段,即图5a中所示的下凹部分;单元4、5、6、8对应与曲线的下降部分。图5中所示的压电驱动器的响应曲线为实际测试结果,模型的误差err=Yn-Fn。根据阈值限制,可以看出在上升阶段最大误差出现在输入电压为25V左右,而下降阶段则较为分散,没有明显的转折点。同时为了实验本模型预测值的有效性,使用由主环曲线推导而来的参数值来预测次环曲线,实验结果如图5b所示。可以看出在电压减小的过程中,预测的位移精度略小于主环精度,但是仍然在控制的精度范围内。

1.压电驱动器响应 2.线性递归计算输出 3.误差曲线(a)主环曲线图 (b)次环曲线图图5 改进型Maxwell滑动模型的输出与实际测量结果比较
从实验结果来看,本改进型Maxwell滑动模型的确能够有效模拟压电驱动器的迟滞现象,并且通过阈值参数的设置,可以较灵活的实现不同系统的定位要求。但是如果需要实现精密控制,则必须设置较小的阈值参数,这将使得构成模型的弹簧滑块单元的数量增加,增加了系统的复杂性。但是在一般应用中,采用0.6~1.0的阈值基本可以满足要求。作者将此改进型Maxwell滑动模型用于江苏瑞祺生命科学研究所研制的CFT-8000型生物细胞显微操作系统中,进行三维工作平台的位姿控制,取得了良好的效果。
3 结论
(1)将传统Maxwell滑动模型的并联结构改为串联结构,使得任一时刻都只有一个弹簧滑块单元处于线性工作区,因此可以降低模型计算量,提高控制效率,并且改进型Maxwell滑动模型能够有效模拟压电驱动器的迟滞现象。
(2)在实际控制系统中,可以通过设定压电陶瓷输出位移测量值与模型的输出值的误差阈值,实现不同系统的定位要求,阈值越小,控制精度越高,但是计算时间越长,实时性变差,因此在实际控制中,需要在阈值大小与控制精度之间进行权衡,以达到较好的控制效果。

