基于序列二次规划法的结构可靠度计算方法*

王林军,邓启程

(三峡大学 机械与动力学院，湖北 宜昌 443002)

0 引言

在结构分析中，通常将失效概率作为判断结构是否可靠的依据，以概率形式为基础的可靠度指标来表达。现有的可靠性分析方法一般采用概率模型，用随机分布来表达不确定变量。目前已经有比较完善的概率可靠性分析技术。姜潮等[1]针对工程实际中的不确定性，引入区间变量并结合概率变量提出了概率-区间混合可靠性分析模型；李昆封等[2]运用一种特殊的椭球凸模型来描述随机变量不确定性，提出了结构凸集-概率可靠性分析的新方法；赵军等[3]提出了广义随机空间中的改进一次二阶矩法，避免了概率变量正交变换过程中的负定问题，同时改善了一次二阶矩法的收敛效率；乔心洲[4]通过定义随机区间安全系数，提出了一种新的结构概率-非概率混合可靠性模型。概率可靠性分析均是基于数学优化算法，对于结构变量维度高、功能函数高度非线性等情况，应用传统的数学优化算法难以解决。智能优化算法的发展为结构可靠性分析及计算开拓了新的思路[5]。姜封国等[6]提出了基于最佳矢量法的混合遗传算法，提升了结构可靠性优化过程中的全局搜索能力，改善了其收敛性；田萍芳等[7]将粒子群算法(PSO)运用到可靠性优化设计中，简化了迭代计算过程，能快速找到最优解[8]，相对于遗传算法，PSO算法不需要梯度信息且可并行搜索，为结构可靠性优化提供了新方向[9-10]；吉猛等[11]提出了一种新的基于同伦分析的功能度量法(PMA)，该方法基于可靠性KKT条件构造同伦方程组，并利用β-core路径跟踪求解，获得了较好的收敛性。这些方法在一定程度上提升了收敛效率，但对于一些极限状态方程非线性程度较大或函数性态较差等问题，其收敛性及计算精度仍存在不足。

针对上述问题，本文引入序列二次规划法(Sequential Quadratic Programmaing，SQP)的约束优化模型并结合结构可靠度指标计算数学模型，将可靠度求解的每一迭代步转换为求解二次规划子问题，根据梯度下降方向搜索最优解，得到可靠度指标最优值及MPP点，保证收敛性的同时提高了计算效率。通过具体算例验证，该方法在保证足够精度的前提下，具有更快的收敛速度及更高的计算效率，同时也表明本文方法在结构可靠度计算中的可行性和有效性。

1 可靠度指标优化模型的建立

二维标准正态空间中可靠度指标β的几何意义如图1所示。正态变量R、S相互独立，其功能方程为：

Z=g(R,S)=R-S=0

(1)

图1中R′O′S′由ROS经过标准正态化变换得到，变换关系式如下：

(2)

其中，μR、σR、μS、σR分别为R和S的均值和标准差。

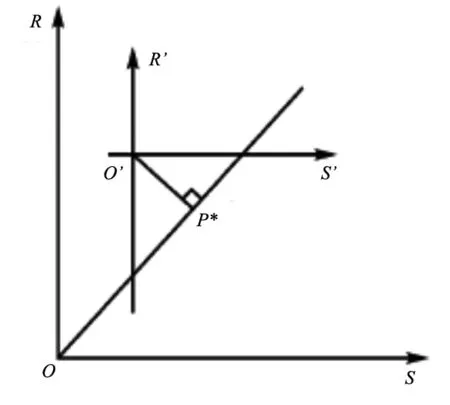
图1 可靠度指标几何意义及验算点示例

在标准正态空间中，极限状态面上距原点O′距离最短的点P*即为验算点，最短距离即为可靠度指标β。含有多个正态参量X1,X2,···,Xn的极限状态方程，β可表示为：

(3)

结构极限状态方程的一般形式为Z=g(X1,X2,···,Xn)=0，其中X1,X2,···,Xn是结构中n个任意分布的独立变量。运用R-F(拉科维茨-菲斯莱法)将非正态变量当量正态化。如图2所示，其基本原理是当量正态化之后的等价正态分布在验算点X*处的累积概率分布函数值(CDF)和概率密度函数值(PDF)分别和原变量在点X*处的CDF值、PDF值相等。

图2 当量正态化原理图

(4)

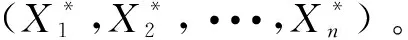
(5)

2 序列二次规划法的优化数学模型

序列二次规划算法最初是由R B Wilson提出[12]，该算法的主要思想是：在求解约束优化问题时，在每一初始迭代点构造一个二次规划子问题，将该子问题的解作为迭代搜索的方向，并选取相应的效益函数确定迭代搜索的步长；通过求解上述子问题修正迭代点，直到二次规划的结果逼近原非线性规划问题的解。一般约束优化问题可表示为：

minf(x)
s.t.hi(x)=0,i∈E={1,···,l}

(6)

则上述约束优化模型(6)的Lagrange函数为：

(7)

其中，μ=(μ1,···,μl)T为Lagrange乘子向量。约束函数h(x)的梯度矩阵为：

▽h(x)=[▽h1(x),···,▽hl(x)]

(8)

则h(x)的Jacobi矩阵为A(x)=▽h(x)T。根据约束优化问题(6)的KT条件，可以得到如下的方程组：

(9)

现在考虑用牛顿法求解方程组(9)。记函数▽L(x,μ)的Jacobi矩阵为：

(10)

其中，

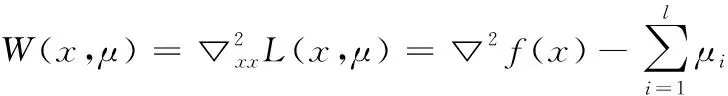
(11)

是拉格朗日函数L(x,μ)关于x的Hessian矩阵。式(10)所定义的矩阵N(x,μ)也称为KT矩阵。对于给定的点zk=(xk,μk)，牛顿法的迭代格式为：

zk+1=zk+pk

(12)

其中，pk=(dk,vk)满足下面的线性方程组：

N(xk,μk)pk=-▽L(xk,μk)

(13)

即：

(14)

对于方程组(14)，在A(xk)行满秩且W(xk,μk)正定的情况下，系数矩阵非奇异且该方程有唯一解，其中式(4)是拉格朗日函数稳定点的KT条件，该方法具有局部二次收敛性质。

详细算法步骤如下，算法流程图如图3所示。

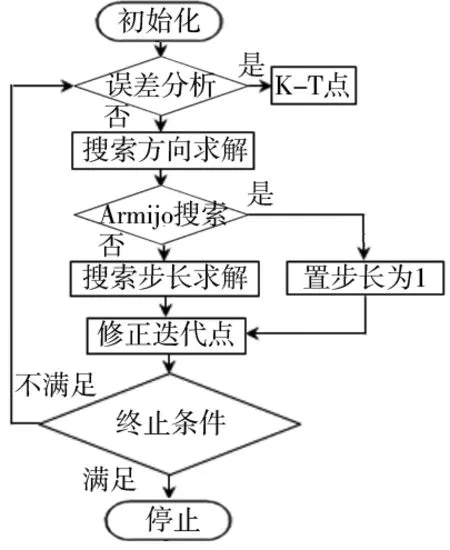
图3 序列二次规划算法流程图

Step 0：给定变量初始点及乘子向量初始值(x0,μ0)∈Rn×Rl，选择参量η,γ∈(0,1)，给定误差0≤ε≤1；

Step 1：计算原问题(6)的拉格朗日函数的梯度矩阵在xk处的值，若‖▽L(xk,μk)‖≤ε，则停算，表示满足容许误差，得到原问题(6)的一个近似K-T点(xk,μk)；否则转向Step 2；

Step 2：求解方程组(14)，确定初始点x及乘子向量μ的搜索方向，记为Pk=(dk,vk)；

Step 3：Armijo搜索。若不等式‖(▽L(xk+dk,μk+vk)‖2≤(1-γ)‖▽L(xk,μk)‖2成立，则置搜索步长αk=1，转向Step 5；否则转向Step 4；

Step 4：令mk是使不等式‖▽L(xk+ρmdk,μk+ρmvk)‖2≤(1-γρm)‖▽L(xk,μk)‖2成立的最小非负整数m，置搜索步长αk=ρmk；

Step 5：修正迭代点。由Step 2- Step 4求得的搜索方向及步长，修正当前迭代点，令xk+1=xk+αkdk，μk+1=μk+αkvk，转向Step 1继续优化求解。若xk+1满足终止条件，则停止迭代，否则重复以上步骤直到获得最优解。

3 算例及分析

3.1 数值算例

结构的功能函数表达式：

(15)

表1 各随机变量分布参数取值情况

表2 可靠性分析结果

计算结果表明，针对上述的结构功能函数，本文提出的方法能够得到精确合理的结果，同一次二阶矩法中的验算点法计算结果相吻合。采用蒙特卡洛验证表明，在满足预定精度的条件下，抽样次数M达到106次时，迭代优化收敛于最优点，该结果与本文提出方法及验算点法的计算结果相吻合，表明本文方法具有足够的精度。

3.2 悬臂梁算例

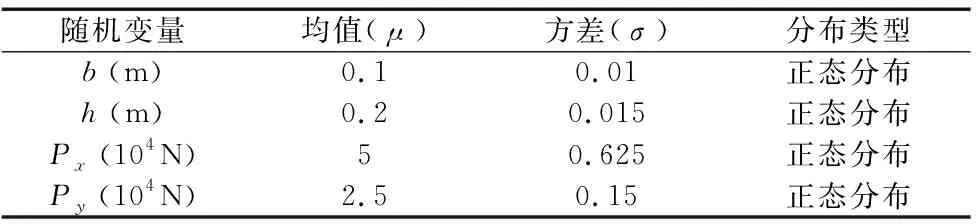
如图4所示的悬臂梁长度为L，横截面宽度为b，高度为h，悬臂梁顶端承受作用力Px，Py，方向如图所示。选用梁的横截面尺寸b与h，以及作用力Px，Py作为随机变量，各变量分布参数取值如表3所示。选择材料的许用应力S与悬臂梁固定端处最大应力的差作为功能函数，得到悬臂梁的极限状态方程：

(16)

其中，L=1m，S=320MPa。

图4 悬臂梁

随机变量均值(μ)方差(σ)分布类型b(m)0.10.01正态分布h(m)0.20.015正态分布Px(104N)50.625正态分布Py(104N)2.50.15正态分布

对于表3中的参数取值情况，采用本文所提出方法，得到可靠度指标及失效概率的计算结果，具体结果如表4所示。

表4 可靠性分析结果

3.3 汽车低速碰撞模型算例

汽车在设计过程中需要对其碰撞安全性进行全面的考虑，以最大程度上减少驾乘人员的损伤，主要通过提高车辆的耐撞性来减轻损伤。车辆碰撞过程中很大程度上是因为车体加速度场过大，驾乘人员撞击车体而损伤。因此，本文将图5中所示的小型轿车以56km/h的时速正面撞向刚性墙体时B柱下端加速度峰值设置为碰撞安全性的参考指标，来评估汽车碰撞安全的可靠性。在车辆耐撞性评估中，纵梁、防撞梁、加强板等元件的吸能性关系到整个车辆的耐撞安全性。在车辆碰撞分析中，通常是通过更改纵梁、防撞梁、加强板等部件的截面结构、厚度、材料等设计参数来改善吸能性能，降低碰撞对乘员带来的伤害。因此本文将防撞梁、前纵梁、前纵梁盖板、加强板等吸能元件作为影响B柱下端加速度的主要因素，考虑这些吸能元件厚度、材料参数的不确定性，并将它们作为分析变量进行汽车正碰安全性的可靠性分析，汽车碰撞模型随机变量及其分布见表5。

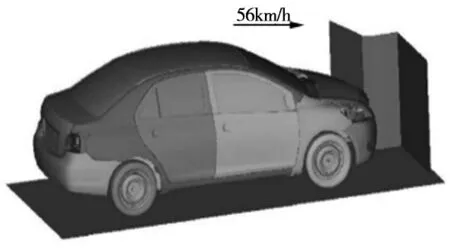
图5 汽车碰撞有限元模型

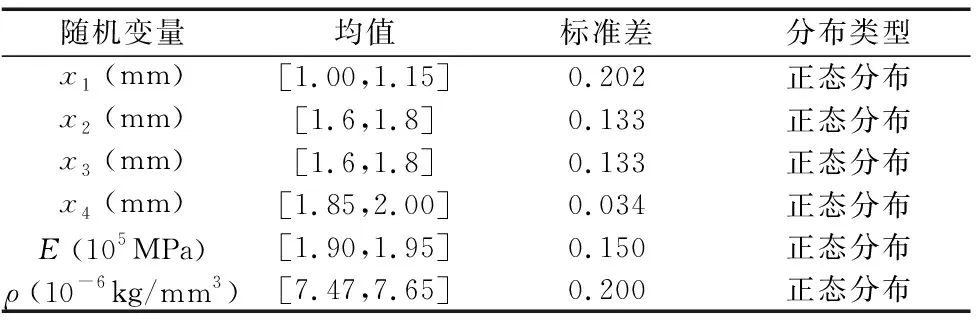
选取如图6中所示的防撞梁厚度x1、前纵梁盖板厚度x2、加强板厚度x3和前纵梁厚度x4及其材料属性弹性模量E、密度ρ作为不确定变量。

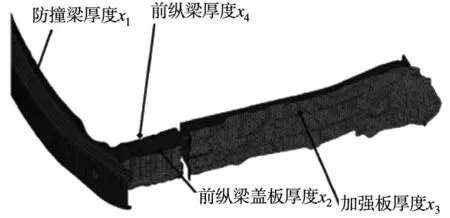
图6 分析变量的选取

随机变量均值标准差分布类型x1(mm)[1.00,1.15]0.202正态分布x2(mm)[1.6,1.8]0.133正态分布x3(mm)[1.6,1.8]0.133正态分布x4(mm)[1.85,2.00]0.034正态分布E(105MPa)[1.90,1.95]0.150正态分布ρ(10-6kg/mm3)[7.47,7.65]0.200正态分布

运用多项式响应面法拟合汽车碰撞的近似模型，运用拉丁方采样法在变量区间内釆取40个样本点，由LS_DYNA计算获得各样本点的加速度响应值。应用归一化方法对所有不确定参数进行无量纲化处理，并在此基础上运用响应面法构造B柱下端加速度峰值的二次响应面模型。功能函数定义为B柱容许的最大加速度amax与有限元仿真中B柱加速度峰值a的差。功能函数为：

g=amax-a(x1,x2,x3,x4,E,ρ)

(17)

根据设计目标给定上式中的amax为393m/s2。为方便画出功能函数响应面曲线图，依据参数的分布，固定x3=1.7，x4=1.93，x5=1.93，x6=7.56，得出功能函数响应面图，如图7所示。从图中可以看出，在固定x3、x4、x5、x64个参数之后，很大程度上降低了原功能函数的非线性，所以功能函数响应面在三维空间中的曲面度很小，近似显示为一个倾斜的平面。图中纵坐标表示功能函数值g的响应值，曲面的倾斜程度分别表示功能函数响应值g对参数x1、x2的敏感程度。可以看出相对于x1，随着x2的变化响应值g的变化更加明显。

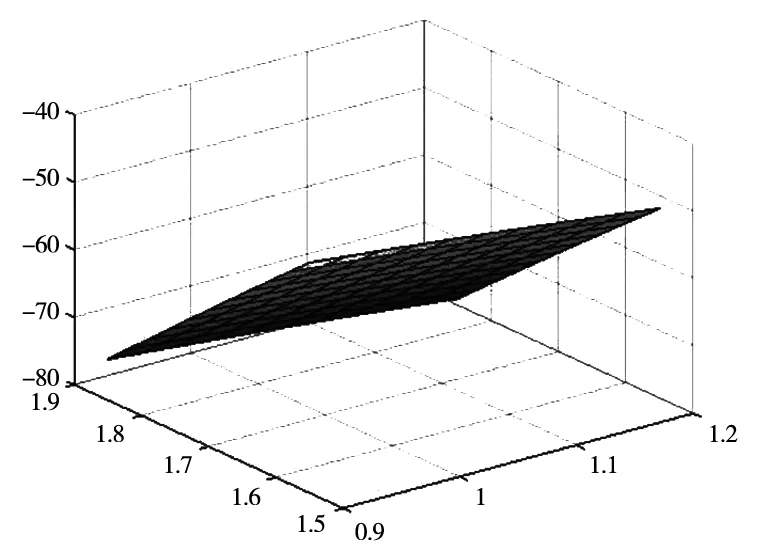
图7 功能函数响应面

汽车碰撞的可靠性分析结果汇总于表6。从分析结果可见，该结构碰撞可靠性最优值收敛于表中所示的MPP点，各随机变量的最优值在均值区间中心点周围的一定范围内波动，波动范围最大的两个参数分别是防撞梁厚度x1及前纵梁盖板厚度x2，分别达到了14.3%和20.6%，这与功能函数响应面图(图7)的分析而结果相吻合，说明防撞梁厚度及前纵梁盖板厚度的结构参数不确定性更加明显，对汽车的碰撞性能影响较大。碰撞可靠度指标β=3.6504且较小的失效概率说明该模型满足给定的加速度上限amax的要求。碰撞模型可靠性对比分析结果汇总于表7，此处将表6结果与JC法、蒙特卡洛模拟法结果进行对比。若以蒙特卡洛模拟(106次抽样)结果为精确值，本文所提方法具有较高的精度，且两者误差在可接受的范围之内；对比JC法的迭代次数(7次)， 本文提出的基于序列二次规划法的结构可靠度计算方法的迭代次数为4次，表明该方法具有较高的计算效率和较快的收敛速度，具有一定的应用价值。

表6 汽车碰撞模型可靠性分析计算结果

表7 碰撞可靠性分析结果对比

4 结论

本文提出了一种基于序列二次规划法的结构可靠度计算方法，该方法充分利用了序列二次规划方法的优点，沿目标函数的下降方向迭代搜索，能快速找到最优解。该方法可解决具有一定非线性程度的结构功能函数的可靠性分析，且有较高的计算效率和收敛速度。算例的结果表明，本文方法相对于现有的可靠性分析方法，在保证合理分析结果的同时有更高的计算效率和收敛速度。本文方法对初始点的选取及效益函数的定义要求较高，后期可以对这些实现细节做深入的研究。本文方法可推广至可靠性优化设计中，具有一定的实际意义。