基于小波分析的淮河干流上游年径流量周期分析研究
沈 丹戴 欢王敬磊
(1.蚌埠市机电排灌管理站 蚌埠 233000 2.河海大学水文水资源学院 南京 210098 3.安徽淮河水资源科技有限公司 蚌埠 233000)
1 引言
淮河发源于河南省桐柏山,自西向东流经鄂、豫、皖、苏四省,主流在三江营入长江,全长约1000km,总落差200m。从河源到洪河口为上游,流域面积3.06万km2,河长360km,多年平均径流量为92.48亿m3(1956~2010年平均值,下同),径流量年内分配不均,年际变化较大。王家坝水文站是淮河干流上游重要的控制站,其1956~2010年径流量过程线见图1。
河川径流序列是一个具有多时间尺度特征的复杂过程,径流的变化规律和丰枯变化趋势在不同的时间尺度下是不相同的,即多时间尺度。所谓多时间尺度变化,其含义就是指研究系统的变化并不存在一种真正传统意义上的周期性,即没有非常明显或者严格的交替循环过程,但是又存在时而以这种周期变化,时而以另一种周期变化,而且在相同的一个时段内,研究系统又同时包括各种时间尺度上的周期变化的现象,即这种肉眼无法观察或从直观数据中无法得到的多时间尺度的周期性和多层次时间尺度结构。所以在刻画径流序列中,水文要素的多时间尺度分析是无法避免的。而小波分析的优势就是在时域和频域上均具有良好的局部化特征和多分辨功能,对于多时间尺度的径流序列,不仅可以对其进行局部化分析,还可以分析其内部精细的结构特征,得到其在不同时间尺度下的周期性和演变情况。
2 小波分析
2.1 小波函数
小波函数指的是具有震荡特性,在有限的区域内能够迅速衰减到0的一类函数(t):
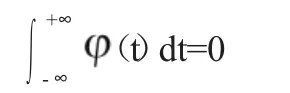

小波函数的类型在小波分析中有重要的指导作用,在水文时间序列中采用复值Morlet小波:

其中要求ω≥5为常数,即取ω=6。复值小波变换比实数形式的小波变换更适应水文序列。它的实部和虚部位相相差π/2,由此可以减少由于实数小波变换所造成对模的改变。
2.2 小波变换

式中:Wf(a,b)称小波变换系数。而在实际工作中,时间序列常常是离散的,如f(kΔt)(k=1,2,…,N;Δt为取样时间间隔),则上式的离散形式为:

从上式知,小波变换公式中同时含有参数a与b,则表明该公式会同时反映出时域参数b和对应频域参数a的变化过程。
Wf(a,b)随频域a和时域b变化,就可以作出时域b为横坐标频域、a为纵坐标的Wf(a,b)的二维等值线图,称为小波变换系数等值线图。不同时间尺度下的小波变换系数的特征值可以反映研究对象在对应的时间尺度下的变化特征:正的小波变换系数对应偏多期,负的则相反,正负小波系数的转折零点则对应突点;小波系数模的绝对值越大,表明该时间尺度变化越显著。通过以上研究,可以分析水文序列多时间尺度演变特性和突变特征。
2.3 小波方差
将所有与时间尺度a有关的小波系数进行积分,就可以得到其小波方差,其公式为:
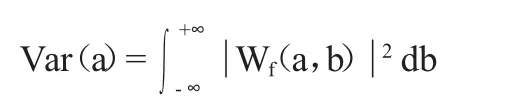
在一定尺度下,小波方差Var(a)数值则表示该时间尺度周期波动的能量大小。小波方差随时间尺度a变化的过程称为小波方差图。小波方差图能够反映出水文时间序列中所包含的不同周期波动及它们的能量大小。因此,通过小波方差图可以简单直观地确定出一个水文时间序列中存在多少个周期,有几个起主导作用的主要周期。
3 淮河干流上游年径流序列的小波分析
用上述小波分析的方法,对延伸后标准化的年径流量序列进行Morlet小波变换,用Matlab绘制出小波系数实部、模的等值线图和小波方差图。

图1 王家坝1956~2010年径流量过程线图

图2 王家坝站1956~2010年径流量序列Morlet小波变换的模时频分布图
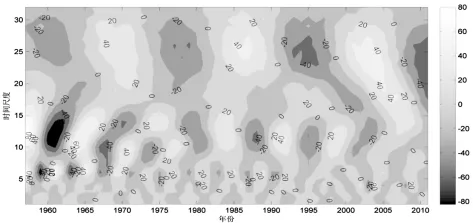
图3 王家坝站1956~2010年径流量序列小波变化实部等值线图
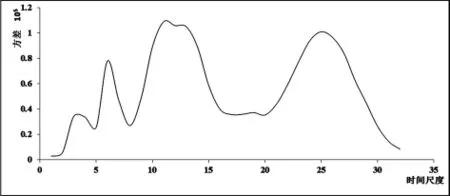
图4 王家坝站1956~2010年径流量序列小波系数方差图

图5 王家坝站年径流变化11a、25a、6a、3a时间尺度的小波系数实部过程线图
3.1 年径流序列小波变化模时频变化分析
从图2中可以看出,研究地区不同时段各时间尺度的震动能量密度时频强弱分布。在25a左右的时间尺度上其能量密度比较强,在时域上分布也比较明显,主要发生在1985~2010年之间,震动中心在2005年左右;在10~15a的时间尺度上,出现了两个震动中心,一个是全局最强震动能量密度,发生在1956~1970年,震动中心在1956年,说明该时间尺度上变化周期最明显。另一个在发生在1983~1996年,震动中心在1990年左右;在5a左右的时间尺度上,也出现震动能量密度较强的中心,发生在1957年左右;在1~5a的时间尺度上,震动能量较强信号发生在1998~2006年,震动中心发生在2003年左右。
3.2 年径流序列小波变化实部时频变化分析
图3是研究区域1956~2010年径流量序列小波系数实部的时频分布图。图中清晰地显示了研究区域径流量序列不同时间尺度变化、突变点分布及位相结构。在时间尺度a相同的情况下,正的小波系数与丰水期相对应;负的小波系数与枯水期相对应;小波系数为零与突变点相对应。可以看出该年径流量序列存在着 0~3a、4~8a、9~15a、16~32a左右的四类时间尺度的变化规律。其中9~15a和16~32a左右的丰枯交替变化最为明显。对于16~32a的时间尺度来说,年径流经历了枯→丰→枯→丰→枯→丰→枯7个交替变化。具体枯水年时段为:1956~1965年、1975~1982年、1991~1999年、2007~2010年,且2010年其实部等值线未闭合,说明在2010年以后可能还会存在一段枯水期。丰水年时段为:1966~1974年、1983~1990年、2000~2006年。
而对于9~15a的时间尺度来说其年径流序列经历了丰→枯→丰→枯→丰→枯→丰→枯→丰→枯→丰→枯→丰→枯→丰→枯16个交替变化。枯水年时段具体表现为:1958~1962年、1967~1968年、1972~1974年、1979~1981年、1986~1989年、1994~1996年、2001~2004年、2008~2010 年。丰水年时段为:1956~1957 年、1963~1966年、1669~1971年、1975~1978 年、1982~1985年、1990~1993年、1997~2000年、2005~2007年。
对于4~8a的时间尺度,周期变化显示较弱,丰枯周期变化竟有13次之多,位相结构不稳定。由此得知该时间尺度下年径流变化有明显的突变特征。同时,对于3a左右的时间尺度,丰枯周期变化更是达到了14次,可知在3a左右的时间尺度下,其年径流突变性较强,周期性较弱。
3.3 年径流序列小波变化方差分析
图4为王家坝站1956~2010年径流量序列小波系数方差图。小波方差图能够反映年径流时间序列的波动幅度随时间尺度a的分布情况,可以用来辨识时间序列中各种尺度的扰动强弱和周期变化特征。由此可以确定年径流变化的主要周期。由图可知:小波方差出现4个较为明显的峰值,依次为3a、6a、11a和25a的时间尺度。其中,11a的时间尺度对应着最大峰值,所以11a左右的时间尺度对应的周期变化最强烈,是其年径流变化的第一主周期。25a左右的时间尺度对应着第二峰值,是其年径流变化的第二主周期;6a左右的时间尺度对应着第三峰值,是其年径流变化的第三主周期;而3a左右的时间尺度对应着最小的峰值,是其年径流变化的第四主周期,相对于前三个主周期第四主周期的周期变化较弱。
绘制第一、第二、第三和第四主周期所对应的小波变换系数实部过程线,如图5所示。
将年径流序列小波变化方差分析与年径流序列小波变化实部时频变化分析结合,可以看出:在王家坝站年径流变化的四个主周期和实部分析中,四类时间尺度的变化规律相对应,并且四个主周期分别是是其时间尺度中心。
4 结论
通过Morlet小波分析法对王家坝站1956~2010年共计55年的年径流序列进行小波变化,结果表明:王家坝站存在 0~3a、4~8a、9~15a、16~32a 左右的四类时间尺度的变化规律,其时间尺度中心分别对应为3a、6a、11a、25a。根据小波方差图可知,11a的时间尺度为年径流变化的第一主周期,25年的时间尺度为其第二主周期,6a的时间尺度为其第三主周期,3a的时间尺度为其第四主周期

