特例法在电路分析中的应用

田社平， 孙 盾， 张 峰

(1.上海交通大学 电子信息与电气工程学院， 上海 200240；2. 浙江大学 电气工程学院, 浙江 杭州 310027)

0 引言

事物的普遍性存在于事物的特殊性之中，而特殊性中也包含着普遍性，特殊性与普遍性是相联系而存在的。将这一哲学原理应用于自然科学领域和工程技术领域，就可以得到解决问题的特例法。

特例法就是用特殊情形代替普遍条件，得出特殊结论，而这一特殊结论亦具有普遍意义。对电路问题而言，这特殊情形包括特殊的电路连接方式，如开路、短路等；特殊的元件参数取值；特定的电路拓扑结构等等。本文结合笔者的教学实际，通过例子来说明特例法在电路中的应用，欢迎大家批评指正。

1 问题的提出与特例分析

问题：如图1(a)所示，N为线性含独立源电阻网络。已知当R=0 Ω时，电压u=3 V；当R→∞时，u=4 V。ab端口的等效电阻Req=5 Ω。试求u与R的一般关系。

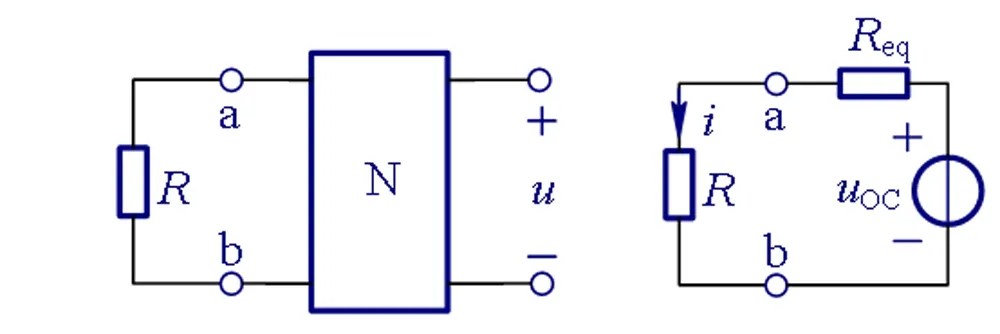
(a) 例1电路 (b) 等效电路图1 采用特例法分析的电路

这是一道公布在“电路教师之家”微信群中的题目，它主要考察电路定理的综合应用能力。为便于比较，这里先给出一般的常见解法如下：

(1)首先应用替代定理，将电阻用电流为i(方向向下)的电流源替代。

(2)由叠加定理可得，输出电压u可表示为u=Ai+B，其中A、B为待求的常数。

(3)由戴维南定理，作出如图1(b)所示的等效电路，易知电流i可表示为

因此

(1)

(4)将已知条件代入式(1)，得到

(5)最后得出解答为

从上述分析过程中可知，上述例子具有较强的综合性，如果对电路定理没有融会贯通的理解，要顺利地给出解答还是有一定挑战性的。但是，如果将网络N特例化，则分析过程就容易理解得多。为了将N特例化，可以假定N为不含受控源(可含独立源)二端口网络，即N可用含独立源的T形电路等效。由于输出端口保持为开路，等效的T形电路右臂的电阻对输出电压无贡献，因此可取该右臂电阻为零；同样由于输出端口开路，等效的T形电路左、右两臂中的等效电压源均可转移至第三条支路中。这样，可将图1(a)中的网络N特例化为如图2中具有明确拓扑结构的网络N，注意，图中已经隐含了条件“ab端口的等效电阻Req=5 Ω”。由题目给定的已知条件，可得

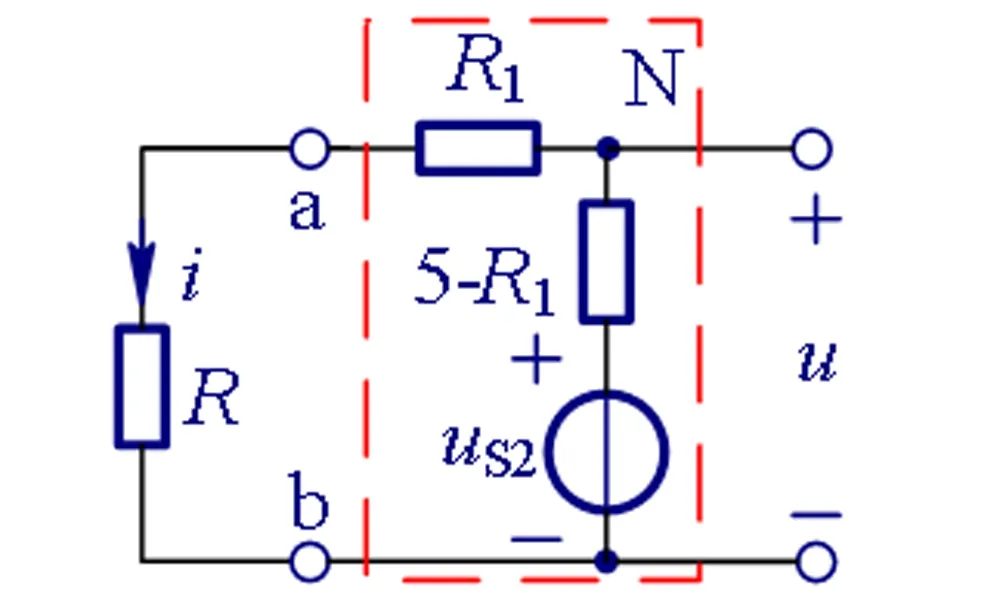
图2 图1(a)电路的特例化

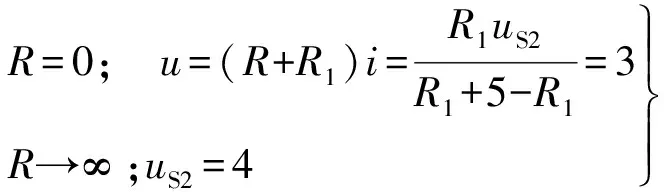
解得

(2)

又由图2，利用式(2)，易知

（2）经济社会发展情况。洞庭湖区位于长江黄金水道与京广交通动脉交汇处，具有承东启西、连南接北的独特区位优势。2016年区域（湖南部分）常住人口约1 692万人，地区生产总值为8 145.4亿元，三次产业结构为12∶46∶42，人均地区生产总值4.8万元，公共财政预算收入705.05亿元，城镇化率50.3%。洞庭湖区自古以来便是“鱼米之乡”和“天下粮仓”，是我国重要的大宗农产品生产基地、最大的水稻产地、商品粮调出地和畜禽水产养殖基地。工业方面初步形成了食品加工、石化、纺织、林纸等支柱产业。近年来，商贸物流、交通运输、生态旅游等现代服务业发展迅速。

相比较而言，上述解法显得非常简洁。上述解答尽管结果正确，但也产生了如下的问题：图2中的网络N是否确实与图1(a)中的网络N在题目给定的条件下等效？或者说，所谓的特例化方法对求解过程是否是充分的？这关系到特例法的合理性及其可应用性。

2 应用特例法的合理性

下面通过分析图1(a)与图2中N的端口特性，来说明应用特例法的合理性。将图1(a)重绘如图3所示 。

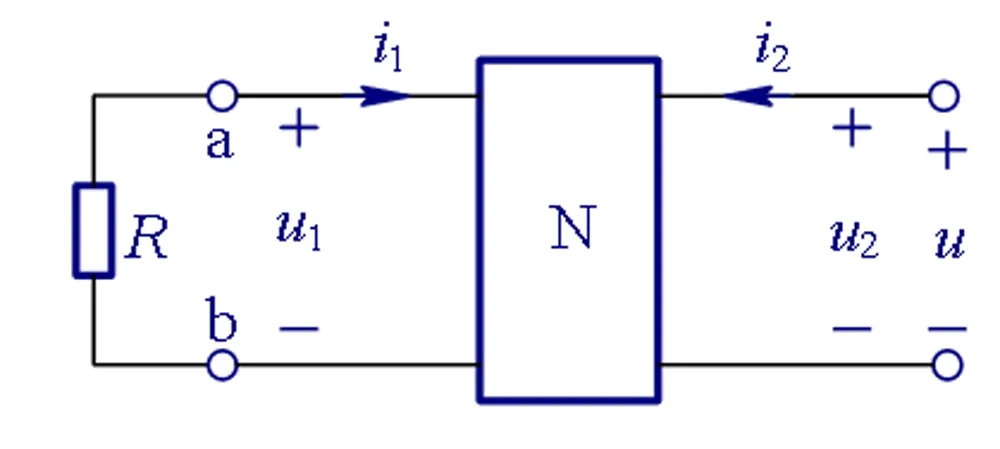
图3 求二端口N特性的电路

不失一般性，假设N的流控型VCR可表示为[1]

(3)

由条件“已知当R=0 Ω时，电压u=3 V”可得

(4)

由条件“当R→∞时，u=4 V”可得

(5)

由条件“ab端口的等效电阻Req=5 Ω”可知，N的端口1的开路正向电阻为5 Ω，亦即

r11=5 Ω

(6)

r21uOC1=5,uOC2=4,r11=5

(7)

上面的分析说明了图2中的N只是图1(a)中N的众多可能网络结构的一种可能的形式，亦即，图2电路的实现方式完全满足题目给定的条件，在题目给定的条件下，图2中的网络N确实与图1(a)中的网络等效。因此，采用图2所示的特例化方案对求解题目是完全充分而合理的。

3 进一步的讨论

由题目给定的条件无法唯一确定图1(a)的网络N的结构，因此特例化N可有多种方案，例如，另一种特例化方案如图4所示。

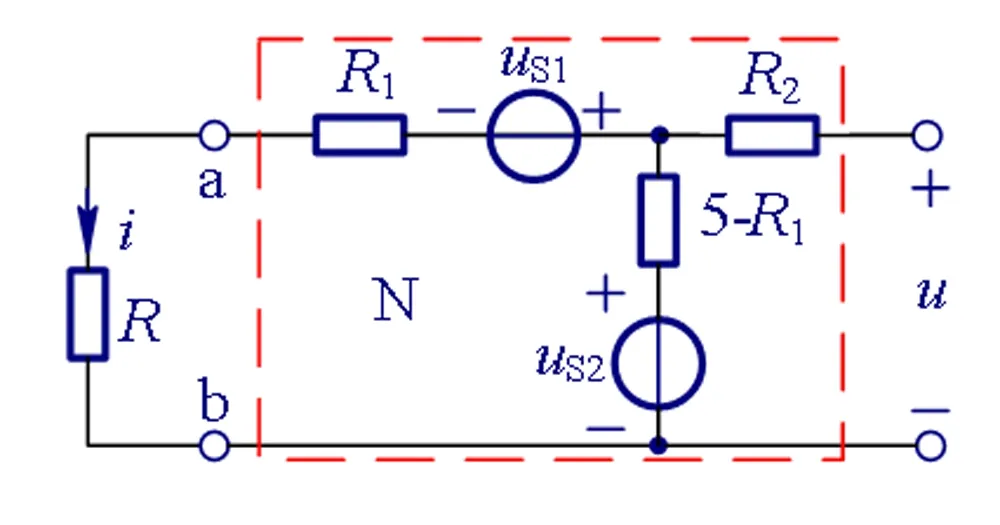
图4 图1(a)电路的特例化之二

同样，与图2类似，图4的特例化方案已经隐含了条件“ab端口的等效电阻Req=5 Ω”。由题目给定的已知条件可得

又由图4，易知

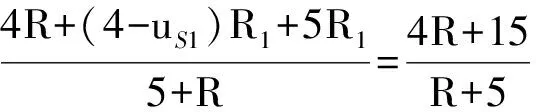
尽管图4中特例化网络N包含冗余的元件，但对分析结果没有影响。

利用二端口网络的等效电路还可进一步分析图1(a)的特例化方案。假设网络N是互易的(r12=r21)，则图1(a)电路可等效为图5所示的T形等效

电路[2]。

图5 图1(a)电路的T形等效电路

事实上，由图5的等效电路及其N的参数条件式(7)，可以构造出无穷多种特例化方案。当然，为求解题目的方便，采用图2所示的特例化方案较为合适。

4 结语

在科学研究和工程技术领域，特例法是一种普遍使用的方法。对某些电路问题，采用特例法可简化分析过程。本文通过对一含不明确拓扑结构电路的分析，说明了特例法的适用性。在电路教学中适当地应用特例法，可起到锻炼学生思维、提高学习兴趣、加深对电路知识的理解等作用。