基于蓄电池模型参数拟和的新型充电控制策略
马里千,许春雨,宋建成,武迪
(1.太原理工大学,太原 030024; 2.太原理工大学 煤矿电气设备与智能控制山西省重点实验室,太原 030024; 3.矿用智能电器技术国家地方联合工程实验室,太原 030024)
0 引 言
随着绿色可再生能源的快速发展,胶体铅酸蓄电池作为目前最具投资和成本效益的储能装置之一被广泛应用到新能源发电系统中[1-2],它的使用寿命直接影响到系统的安全可靠运行。相应的胶体铅酸蓄电池充电技术成为目前研究的热点。
针对胶体铅酸蓄电池有多种充电方法,恒流、恒压、恒流-恒压充电都属于传统充电方法[3],它们都有各自的优缺点。为了进一步提高充电速率和效率,国内外学者相继提出了一些改进充电方法,比如:间歇式充电方法、脉冲式充电方法、多阶段充电方法等[4]。要实现蓄电池最优充电除了要合适的充电方法外还要选择相应的控制策略来实现对充电电流的精确控制[5]。
以PI控制器为基础的充电控制策略已经被广泛应用到蓄电池充电器中,并取得良好的控制效果[6-10]。文献[6]设计了平滑切换机制来解决充电阶段切换过程中电流断续的问题,但在切换过程中充电电流波动较大。文献[7]虽然解决了上述问题但是缺少对系统稳态性能的分析。文献[8]在传统PI控制的基础上加入了模糊控制,提高了控制精度,但同时增加了计算量和系统的复杂性。文献[9]通过引入遇限削弱积分算法来消除双PI环积分饱和现象,但是在恒压充电阶段充电电流波动较大。文献[10]在PI控制的基础上通过改变硬件电路拓扑来实现充电阶段的平滑切,但是该方法需要特定的拓扑电路来实现,局限性较大,不易推广。
文章以胶体铅酸蓄电池模型的基础,通过实验数据拟和出模型参数,采用三阶段充电方法(恒流-恒压-浮充(CC-CV-FC)充电),在传统单-双闭环PI控制的基础上,提出了一种基于电流预测控制的蓄电池充电控制策略,用电流预测控制器来取代传统单-双闭环PI控制器中的电流环,简化控制器复杂程度的同时提高了系统控制性能,避免充电切换过程中由于PI控制参数改变造成充电电流断续失控的情况。
1 充电系统数学模型
1.1 系统结构
在新能源发电系统中蓄电池一般通过双向DC-DC变换器与直流母线相连。选用非隔离双向半桥DC-DC变换器作为该功率变换单元,具体电路拓扑如图1所示。蓄电池接变换器低压侧,变换器高压侧接直流母线,Cbus、Cbat为滤波电容,L为电感,Q1、Q2为开关管,系统开关频率20 kHz。
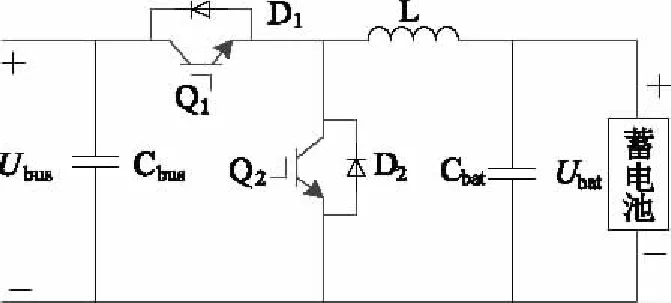
图1 系统主电路拓扑
1.2 蓄电池模型建立及参数识别
由于蓄电池在充电过程中是电化学反应,具有显著的非线性与时变性,而充电系统的精确设计对电池模型及其参数适应性要求较高[7]。按照建立模型的复杂程度,电池模型大致可分为电化学模型、神经网络模型和等效电路模型[10-11]。考虑等效电路模型具有建模简单、参数易于辨识的优点,决定采用二阶RC等效电路模型,电池放电模型如图2所示。

图2 蓄电池放电模型
当蓄电池处于放电状态时,其端电压Uo可表示为式(1):
Uo=E-UΩ-(U1+U2)=E-IbRΩ-
(IbR1(1-et/τ1)+IbR2(1-et/τ2))
(1)
式中RΩ为蓄电池欧姆等效电阻;R1、C1分别为电化学极化等效电阻与电容;R2、C2分别为浓度极化等效电阻与电容;Ib为蓄电池放电电流;E为开路电压;UΩ为欧姆电压降;(U1+U2)为极化电压。
通过脉冲放电法对相关参数进行识别,试验用单节12 V/17 Ah胶体铅酸蓄电池,放电电流为15 A,放电时间为10 s,图3为蓄电池脉冲放电过程中端电压变化曲线。

图3 脉冲放电电压变化曲线
从图3放电电压波形可以看出,蓄电池从开始放电到放电完毕稳定后要经过四个阶段:
(1)开始放电时,蓄电池端电压瞬间降低,这是由于蓄电池欧姆内阻引起的压降,称为欧姆压降,可表示为:
UΩ=IbRΩ
(2)
(2)放电过程中,随着放电时间的增长蓄电池端电压逐渐下降,这一现象主要是由电池的极化作用引起的,由于极化作用引起的电压变化称为极化电压,可表示为式(3):
Up=U1+U2=IbR1(1-et/τ1)+IbR2(1-et/τ2)
(3)
(3)放电结束时,蓄电池端电压瞬间回升,这一现象也是由于蓄电池欧姆内阻引起的,同式(2)。
(4)
(4)放电结束后,蓄电池端电压逐渐回升直到趋于一个稳定值,这是由于放电结束后极化作用逐渐消失引起的,可表示为式(5)
(5)
记录蓄电池每次放电过程中阶段(1)和阶段(3)蓄电池端电压瞬时变化值,根据式(2)、式(4)计算蓄电池欧姆电阻为:RΩ=47.8。
根据实测波形数据,取蓄电池放电阶段(2)和阶段(3)电压变化曲线进行曲线拟合,这里采用二维指数拟合,拟合曲线如图4所示。

图4 模型放电拟和曲线
从图4中可以看出蓄电池极化电压近似按指数函数规律减少或增加,正好与RC电路放电近似指数变化规律是相似的,故电池等效模型由RC表示是合理的。曲线拟合关系如式(6)和式(7)。
f1(x)=a1eb1x+c1ed1x
(6)
f2(x)=a2eb2x+c2ed2x
(7)
式中a1=0.564 5,b1=-0.448 1,c1=11.84,d1= 4.127e-5,a2=13.18,b2=-3.676e-4,c2=-0.563 4,d2=-0.448 8结合式(3)和式(5)可得蓄电池放电模型中各个物理量参数:R1=24 mΩ,C1=
60.2 F,R2=0.3 mΩ,C2=9 F。
2 充电控制器
2.1 传统充电控制器
传统单-双闭环PI控制方法控制框图如图5所示,第一阶段恒流充电通过电流单闭环控制来实现,在第二阶段恒压充电模式和第三阶段浮充充电模式时,充电器通过控制输出电压来调节输出电流,故需要电压外环电流内环级联控制结构。

图5 传统充电控制器控制框图
2.2 基于电流预测控制的充电控制器设计
2.2.1 电压外环控制环路设计
通常情况下,电池在充电过程中其端电压变化缓慢,同时为了避免电压外环与电流内环之间相互干扰,电压外环的带宽应远小于电流内环带宽。因此,在设计电压外环时,将内环近似等效为一阶惯性环节,即:
(8)
式中Tr为电流内环等效时间常数,这里Tr=2e-4s。由于控制量均为直流量故采用PI控制器,电压外环开环传递函数为:
(9)
式中Kp2、Ki2分别为电压外环控制参数,根据闭环传递函数和主导极点的思想可计算出恒压充电控制器控制参数为:Kp2=0.1,Ki2=50。
2.2.2 内环电流预测控制器设计
在传统电压外环、电流内环的基础上,以电流预测控制器来替代电流内环,具体设计思路如下:
建立蓄电池充电电路等效模型,如图6所示。当系统工作在充电模式时,Ubus通过功率变换器给蓄电池组供电,稳定情况下,C1上的电压Ubus也是恒定的,所以Cbus对功率变换没影响,所以在建立蓄电池充电模式等效电路时可以不计母线电容Cbus,图中Ts表示开关管开关周期。

图6 Buck模式等效电路
由图6可知,当双向DC-DC变换器工作在Buck模式开关管S1导通时,其电压方程为:
(10)
开关管S1关断时,其电压方程为:
(11)
将式(8)和式(9)离散化,离散化步长为T,则可得:
(12)
(13)
假定Buck变换器在一个开关周期内,开通占空比为d,式(12)等以d与式(13)乘以(1-d)两式相加得:
(14)
由式(14)可得Buck变换器在一个PWM周期开通的占空比d为:

(15)

(16)
综合以上分析,基于电流预测控制的蓄电池充电控制框图如图7所示。当蓄电池进行恒流充电时电压外环饱和,输出限副,此时充电器输出恒定电流。当蓄电池进行恒压充电和浮充充电时电压外环退出饱和状态,此时充电器通过控制输出电压来调节输出电流。由式(16)可知:采用电流预测控制减少了对控制参数的设计与计算,避免了充电切换过程中由于控制参数的改变造成充电电流断续的情况,蓄电池充电电路输出电流可以在下一周期快速达到给定电流,实现无差拍跟踪。因此该方法有很好的控制性能。
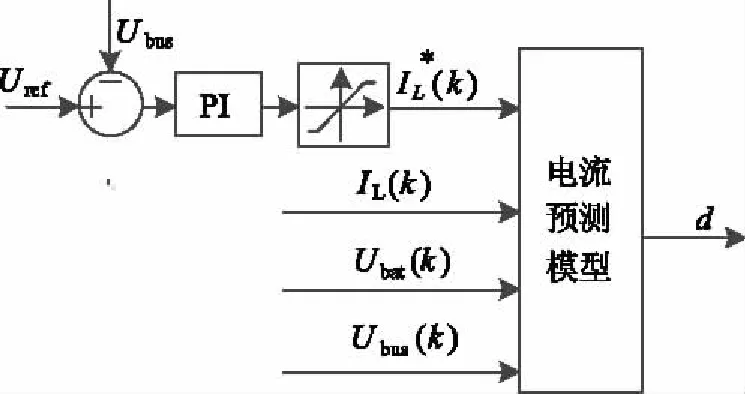
图7 基于电流预测控制的蓄电池充电控制策略
3 仿真及实验结果分析
3.1 仿真验证
根据控制器的设计对蓄电池充电系统进行仿真分析。图8为充电电流阶跃响应仿真波形,从图中可以看出启动充电电流没有超调量且稳态误差为零。图9为充电阶段切换仿真波形,从仿真结果可以看出在切换点前后恒流和恒压两个阶段控制稳定,在切换点处过渡平滑,充电电流连续,满足预期效果。

图8 充电电流阶跃响应仿真波形
3.2 实验验证
为进一步验证上述理论分析结果,按照表1所示系统参数搭建蓄电池充电平台。充电系统采用直流电源供电,充电对象选用胶体铅酸蓄电池,额定电压12 V,额定容量17 Ah。根据相关标准确定蓄电池恒流充电电流和恒压充电电压,在恒流充电阶段充电电流为2.55 A,蓄电池端电压增大到14.4 V后,进入恒压充电阶段,充电电压稳定在14.4 V充电电流由2.55 A逐渐减小。

图9 充电阶段切换仿真波形

参数数值系统工作频率f/kHz20直流源输出电压/V45 V高压侧电容/μF1 500低压侧电容/μF840电感/mH10
图10所示为恒流充电模式时充电电流Ib启动和稳态实验波形,从实验波形可以看出充电电流启动超调量极小,而且稳定后稳流精度可以达到0.7%满足蓄电池充电要求。

图10 恒流充电启动实验波形
图11所示为蓄电池恒流充电切换到恒压充电时的充电电压和充电电流实验波形,从图中可以看出在切换点前充电电流(2.55 A)基本不变,充电电压逐渐增大,当蓄电池端电压达到切换电压(14.4 V)时,充电器由恒流充电模式转换为恒压充电模式,此时充电电压(14.4 V)保持不变充电电流逐渐减小。在切换点处充电电压和充电电流过度平滑切换并没有出现断续震荡的情况,满足预期设计目标和实际蓄电池充电要求。

图11 恒流充电到恒压充电切换波形
4 结束语
在传统单-双闭环PI控制的基础上,提出了一种基于电流预测控制的蓄电池充电控制策略,用电流预测控制器来取代传统单-双闭环PI控制器中的电流环,通过理论分析和实验验证可以得到以下结论:
(1)电流预测控制与传统PI控制方法相比较,提高了系统的动态性能更适合于蓄电池充电系统;
(2)采用电流预测控制器来取代电流内环,减少了对控制参数的设计与计算,避免了充电切换过程中由于控制参数的改变造成充电电流断续的情况;
(3)通过在硬件电路实现基于电流预测控制的蓄电池充电策略,证明了该控制方法的有效性和实用价值。

