一种改进果蝇算法优化神经网络短期负荷预测模型*

王亚琴， 王耀力，王力波，常青

(太原理工大学 信息与工程学院，山西 晋中 030600 )

0 引 言

提高短期负荷预测精度可以为电力系统的运行提供保障，也有助于高效的能源决策和能源管理，还可以减少系统的运行成本[1]。然而，由于气象和温度等多重因素的影响，准确的预测负荷是一项具有挑战性的任务。为了在负荷预测模型中能更好的结合各种影响因素，基于人工神经网络的预测模型得到了深入的研究。其中，BP神经网络由于不需要先验知识、具有自学习的非线性拟合能力，成为了公认的有效的短期负荷预测模型[2-5]。但是传统的BP神经网络用于预测时存在很多不足，如收敛速度慢、初始参数的选取对网络的训练速度影响较大、容易陷入局部最优解和网络泛化能力弱等。

为了提高负荷预测的精度，1991年T. M. PENG等学者从改进神经网络结构方面入手提出了一种改进的BP神经网络算法[6]，该算法在网络结构上表现为在BP神经网络基础上加入了从输入层到输出层的连接，形成了从输入映射到输出的线性和非线性的组合模型，该模型相比BP神经网络模型的性能有了很大的提高，但是该方法并没有得到进一步的研究与发展。Ren和Suganthan在2016年采用随机向量法实现函数连接的(Random Vector Functional-link, RVFL)网络对短期负荷预测进行了研究，结果进一步表明从输入到输出的连接对网络预测性能起着非常重要的作用[7]，不仅可以减少隐含层所需的神经元个数，降低网络在训练过程中调整的参数个数，还可以提高电力负荷的预测精度和网络的泛化能力。此外，负荷预测模型的性能与网络初始连接权值、阈值等参数密切相关，因此要建立精确的短期负荷预测模型，首先要选择合理的初始化参数。目前，随着仿生学的发展，优化网络初始参数的方法有粒子群算法[8]、蚁群算法[9]和蜂群优化算法[10]等，但这些算法均存在参数多、难于理解和寻找全局最优解的过程较缓慢等不足，难以找到全局最优的网络初始参数。

2011年台湾某学者通过模拟果蝇的觅食行为提出了一种果蝇优化算法(Fruit fly Optimization Algorithm，FOA)[11]，和上面几种优化算法相比，它具有参数少、程序简单、易于理解和收敛速度快等优点，在短短的几年时间内获得了很高的关注，如今已广泛的应用在数学函数优化[12]、多维背包问题[13]、无等待流量流程调度[14]、电力负荷预测[15]等方面。FOA的性能主要取决于果蝇种群大小、迭代次数、初始位置和搜索步长的值。其中，搜索步长对果蝇群体的寻优能力有很大的影响[16]。针对基本FOA中搜索步长是个定值，存在后期局部寻优能力弱、收敛速度慢的不足，本文提出了一种改进的果蝇优化算法(Improved Fruit fly Optimization Algorithm，IFOA)用于优化神经网络的初始连接权值和阈值，即通过引入动态衰减因子来动态调整搜索步长，以实现算法全局寻优能力和局部寻优能力之间的动态平衡。

因此，首先采用在BP神经网络中加入从输入到输出的连接的网络(Back-Propagation Neural Network With Direct Input-to-Output Connections, BPNN-DIOC, 直连BP神经网络)，减少隐含层所需的神经元个数，加快网络训练速度。然后利用IFOA优化神经网络的初始连接权值和阈值，以改善算法的寻优能力。最后，综合IFOA和BPNN-DIOC构建了基于IFOA优化BPNN-DIOC的负荷预测模型。

1 直连BP神经网络描述

文献[6-7]的结果表明在神经网络结构中加入从输入到输出的连接对网络的预测性能起着非常重要的作用。受上述工作的启发，本文采用BPNN-DIOC，即直连BP神经网络用于电力负荷预测。直连BP神经网络的拓扑结构图如图1所示，红色箭头表示从输入神经元到输出神经元的直接连接。可以看出，该网络和BP神经网络的主要区别在于直连BP神经网络加入了从输入到输出的连接，形成了从输入映射到输出的线性和非线性的组合模型，从而使网络具有了从输入到输出的线性映射能力。

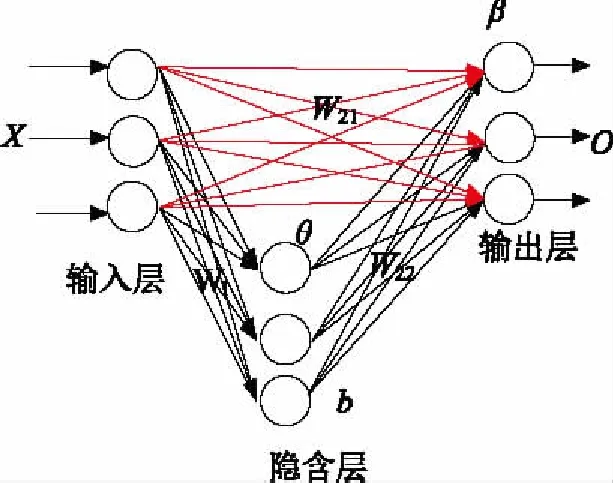
图1 直连BP网络结构拓扑图

直连BP神经网络的学习过程为：

隐含层输出：

(1)

相应的输出层输出为：

O=∑W21X+∑W22b+β

(2)

(3)

式中X表示训练样本的输入数据；W1是输入层到隐含层的连接权值；θ是隐含层阈值；f(·)是输入层到隐含层的激励函数，文中采用logsig函数，具体表达式为式(3)。W22是隐含层到输出层的连接权值；β是输出层阈值；b是隐含层输出；W21是输入层到输出层的连接权值，和网络其它连接权值一样也是随机生成的；O是输出层输出。

2 FOA及改进

2.1 基本FOA

FOA是台湾某学者于2011年提出的一种群体智能算法[11]，是一种基于果蝇觅食行为的新的全局优化方法。果蝇具有敏锐的嗅觉和视觉，刚开始，它通过嗅出漂浮在空气中的各种气味来检测食物源，并飞向相应的地方。然后，在接近食物源后，它可能会找到食物或者以其敏锐的视觉飞到其同伴的聚集地。

对于FOA，它主要包含两个步骤。在利用嗅觉觅食阶段，一群果蝇在群体位置周围随机搜寻食物。然后在视觉阶段，利用敏锐的视觉飞向群体的最佳位置。重复这两个步骤直到达到终止条件。该算法概述如下：

Step1: 初始化果蝇群体：种群大小sizepop，最大迭代次数maxgen，果蝇群体位置(X_axis,Y_axis);

Step2: 赋予果蝇个体利用嗅觉搜寻食物的随机方向与距离的能力，L0为果蝇个体搜索步长。

Xi=X_axis+L0×(2×rand()-1)

(4)

Yi=Y_axis+L0×(2×rand()-1)

(5)

Step3: 由于最优解的具体位置未知，因此先计算果蝇个体与原点间的距离Di，再计算味道浓度判定值Si，此值为距离的导数。

(6)

Si=1/Di

(7)

Step4: 把Si带入设定的味道浓度判定函数，求出该果蝇个体的味道浓度Smelli=F(Si);

Step5: 找出果蝇群体中味道浓度最低(最高)的果蝇:

[bestSmellbestindex]=min/max(Smell)

(8)

Step6: 保留最佳浓度值与x，y坐标，此时果蝇群体利用视觉飞往该位置。

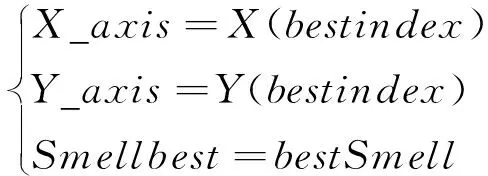
(9)

Step7: 进入迭代寻优，重复执行步骤step2～step5。如果满足条件，返回最优果蝇个体。如果不满足，则继续迭代寻优。

2.2 改进FOA

在FOA迭代寻优的步骤2中，搜索步长L0为固定值，即每代果蝇群体的个体在利用嗅觉寻觅食物时都是以固定半径L0向周围随机搜索的。显然，在果蝇群体个数一定的情况下，步长越大，果蝇个体的搜索空间越大，全局搜索能力越强，但其局部寻优能力会降低；反之，若步长过小，则果蝇个体的搜索空间较小，增强局部寻优能力的同时会削弱全局寻优能力，且易造成果蝇个体陷入局部最优。可见，在FOA中，合适的步长直接影响算法的执行效率。因此，在运用果蝇算法解决实际问题时，必须选择合适的步长值，使之既有较强的全局搜索能力以免陷入局部最优，又具有较好的局部寻优能力以提高搜索的精度。

许多学者针对基本FOA步长固定的缺点提出了改进算法，某些学者提出了一种递减步长果蝇优化算法(Diminishing Step fruit Fly Optimization Algorithm, DS-FOA)[17]，该算法随着迭代次数的增加逐步减小其搜索步长，即将固定步长变为递减步长，式(10)为DS-FOA算法中搜索步长L0满足的函数关系式。

(10)

式中L0为初始步长值；maxgen为设定的最大迭代次数；gen为当前迭代次数。

在DS-FOA中，搜索步长L对应的衰减因子如图2所示，可以看出，它并不能较好地保证算法的全局寻优性能，在一定程度上降低了FOA算法的全局寻优能力。因此，综合考虑基本FOA算法、DS-FOA算法中存在的问题，通过动态改变衰减因子，从而动态改变果蝇群体搜索步长L，提出了采用动态搜索步长的改进果蝇优化算法IFOA。IFOA中衰减因子及搜索步长的表达式如式(8)、式(9)所示，且随着迭代次数的变化趋势如图1所示。

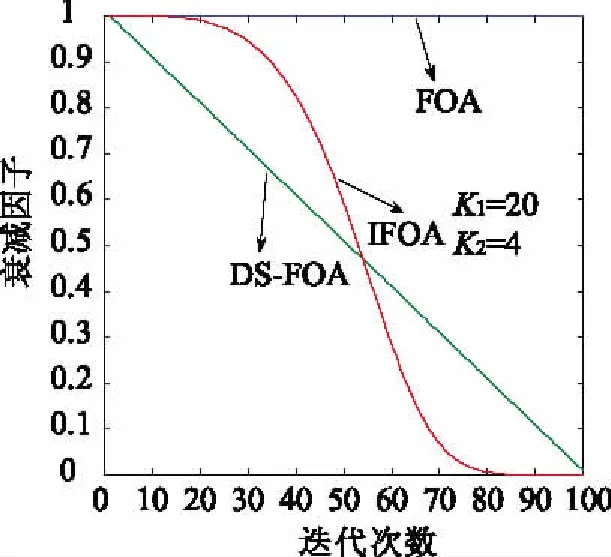
图2 衰减因子和迭代次数之间的关系

可以看出，当k1=20，k2=4时，本文提出的IFOA与DS-FOA、FOA相比，在迭代前期的全局搜索能力和后期的局部搜索能力可以达到较好的动态平衡，从而大大提高果蝇算法的寻优能力。

(11)

L=L0×ω

(12)

3 IFOA优化神经网络

由于神经网络随机生成的初始连接权值和阈值对网络性能有很大的影响，利用IFOA的寻优能力用于优化网络的初始参数，然后在网络训练过程中采用LM算法不断调整网络的连接权值和阈值，直至达到训练停止条件。IFOA优化神经网络的流程图如图3所示。

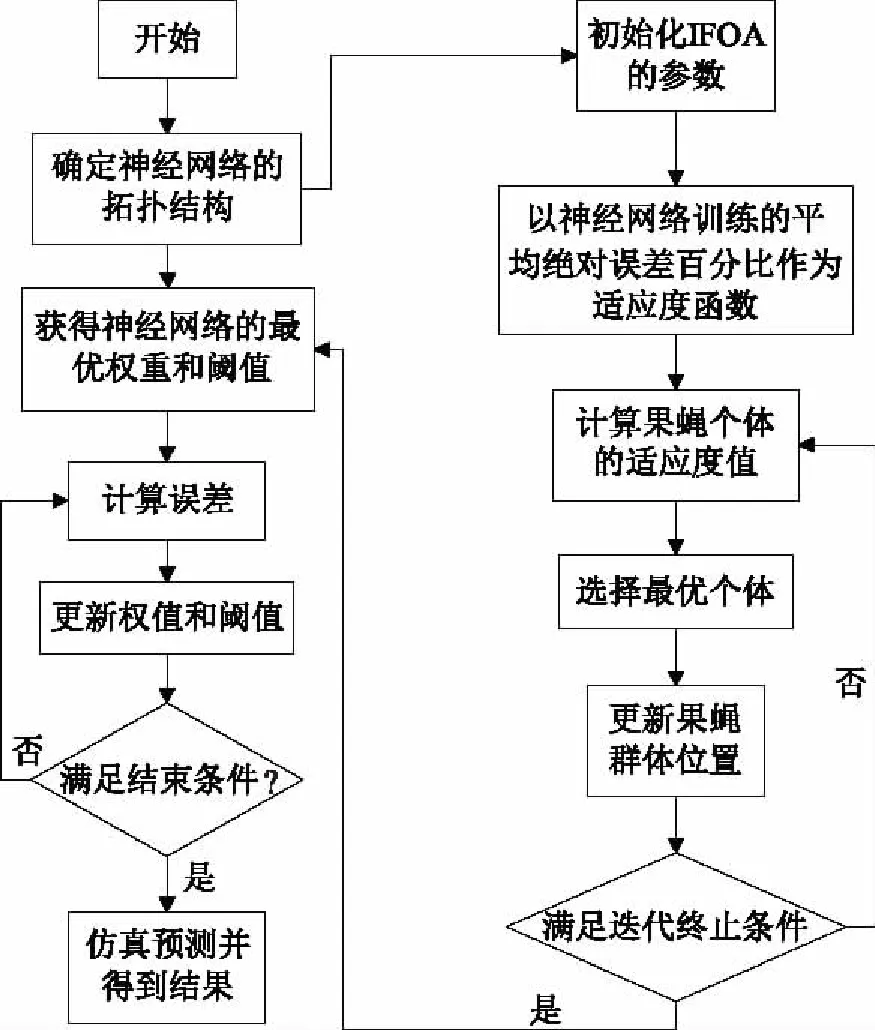
图3 IFOA优化神经网络的流程图

且详细步骤如下：

Step1: 确定神经网络的网络拓扑结构;

Step2: 初始化种群大小、果蝇个体的位置以及最大迭代次数等参数。其中每个果蝇个体包含神经网络的初始连接权值和阈值;

Step3: 赋予果蝇个体利用嗅觉搜寻食物的随机方向与距离的能力，L0为果蝇个体初始搜索步长。

(13)

Xi=X_axis+(2×rand()-1)×L0×w

(14)

Yi=Y_axis+(2×rand()-1)×L0×w

(15)

Step4: 先计算果蝇个体与原点间的距离Di，再计算味道浓度判定值Si。

(16)

Si=1/Di

(17)

Step5: 把Si带入设定的适应度函数，即味道浓度判定函数，求出果蝇个体的适应度值。本文以预测结果的平均绝对误差百分比(MAPE)作为果蝇个体的适应度函数，它定义为：

(18)

式中Yi是网络输出反归一化后的负荷；Ti是原始负荷；n表示数据的个数;

Step6: 找出果蝇群体中味道浓度最低的果蝇，也就是MAPE的最小值。

[bestSmellbestindex]=min(Smell)

(19)

Step7: 保留最佳浓度值与x，y坐标，此时果蝇群体利用视觉飞往该位置;

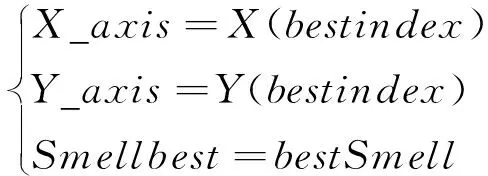
(20)

Step8: 进入迭代寻优过程，重复执行步骤2～步骤6。判断适应度函数值是否低于上一次迭代的值，如果是，则执行步骤7更新群体的最优适应度值并保留最佳位置；如果不是，则返回步骤2～步骤6继续迭代寻优，直到达到结束条件为止;

Step9: 找到全局最优个体后，将其解码为神经网络的初始连接权值和阈值;

Step10: 采用LM算法对经过IFOA优化的神经网络进行训练及预测。

4 短期电力负荷预测模型

4.1 数据预处理

短期电力负荷受经济因素、时间因素、气象因素和紧急事件等多种因素的影响，其中，气象因素对电力负荷的影响尤为明显。为了实现对不同类型的数据进行统一分析以提高预测准确性，首先需要将原始数据进行归一化处理。在文中，按式(21)将原始负荷数据归一化到 [0,1]，之后将预测输出值按式(22)反归一化为实际负荷。其中，T代表原始负荷，Tmax和Tmin是原始负荷的最大、最小值，y表示归一化后的负荷，Y是反归一化后的负荷。另外，式(21)、式(22)所示的归一化方法很难描述温度和日期类型等因素与电力负荷之间的关系，因此，对温度进行如表1所示的归一化处理。

表1 温度归一化

对日期类型取工作日为0.1，休息日为0.9。

(21)

Yi=yi×(Tmax-Tmin)+Tmin

(22)

式中Ti代表原始负荷；Tmax和Tmin分别是原始负荷的最大、最小值；ti表示原始负荷归一化后的负荷；yi为归一化的网络输出负荷；Yi是网络输出反归一化后的负荷。

4.2 确定神经网络拓扑结构

本文以澳大利亚能源市场运营商(Australian Energy Market Operator，AEMO)[18]新南威尔士州2015年9月份的数据为例构建短期电力负荷预测模型。将预测日前两天以及预测日前一周的电力负荷数据、温度和日期类型作为构建短期负荷预测模型的输入因子，而将预测日某一时刻t的电力负荷作为网络的输出。选取的具体的输入神经元如表2所示。

表2 网络的输入变量(t表示预测时刻)

4.3 仿真结果及分析

选取2015年9月1日～27日的数据作为训练样本，分别构建了BP神经网络(BPNN)、直连BP神经网络(BPNN-DIOC)、FOA优化的BP神经网络(FOA-BPNN)、DS-FOA优化的BP神经网络(DS-FOA-BPNN)、IFOA优化的BP神经网络(IFOA-BPNN)以及IFOA优化的直连BP神经网络(IFOA-BPNN-DIOC)六个不同的网络模型用于电力负荷预测。为了比较该六种模型在预测性能方面的好坏，采用预测输出的平均绝对误差百分比(Mean Absolute Percentage Error, MAPE)和均方根误差(Root Mean Square Error, RMSE)作为模型的评价指标。此外，将MAPE作为果蝇优化算法的味道浓度判定函数(适应度函数)，找出果蝇群体中味道浓度最小的果蝇，即找出MAPE的最小值。MAPE和RMSE的定义如下：

(23)

(24)

式中Ti代表原始负荷；Yi是网络输出反归一化后的负荷；n为数据的长度。

仿真平台为MATLABR2012a，利用以上六种模型分别预测9月28日24小时内的电力负荷需求。表3为在相同初始条件下六种模型的预测结果，从中可以得出以下结论：

(1)M3与M1相比、M6与M5相比，说明采用直连BP神经网络可以减少隐含层所需的神经元个数，降低网络在训练过程中调整的参数个数，加快网络训练速度，从而提高电力负荷的预测精度及网络的泛化能力；

(2)M2、M4、M5与M1相比，M6与M3相比，说明采用果蝇算法优化神经网络的初始连接权值和阈值可以改善网络的全局寻优能力，从而提高网络的预测性能；

(3)M5、M4和M2三个模型相比，本文提出的IFOA方法可以改善基本FOA方法中因搜索步长固定造成的后期局部寻优能力弱的缺点，也可以改善DS-FOA方法中由于线性成比例递减步长造成全局寻优能力减弱的缺点，从而使得算法在迭代前期具有很好的全局寻优能力的同时又在迭代后期具有较好的局部寻优能力；

(4)M6、M5与M1相比，说明本文构建的IFOA-BPNN-DIOC模型与文中其它模型相比可以大大减少网络在训练过程中调整的参数个数，加快网络的训练过程，提高网络的预测能力和泛化能力，是一种高效的短期负荷预测模型。

表3 六种不同模型的预测结果

5 结束语

为了提高神经网络负荷预测模型的性能，提出了一种直连BP神经网络和改进果蝇优化算法的组合模型用于短期负荷预测。首先采用直连BP神经网络构建负荷预测模型，以减少网络训练过程中调整的参数个数以及提高网络泛化能力。然后利用IFOA优化神经网络的初始连接权值和阈值，以改善算法的全局寻优能力。最后，构建了一种IFOA优化BPNN-DIOC的短期负荷预测模型。为了探究所提模型的有效性，分别构建了BPNN、BPNN-DIOC、FOA-BPNN、DS-FOA-BPNN、IFOA-BPNN以及IFOA-BPNN-DIOC六个不同的网络模型用于负荷预测。结果表明，采用直连BP神经网络负荷预测模型可以大大简化网络结构，提高网络的预测精度。而所提出的改进果蝇优化算法相比基本既有较强的全局搜索能力以免陷入局部最优，又具有较好的局部寻优能力以提高搜索的精度。因此，构建的基于IFOA优化BPNN-DIOC的负荷预测模型具有更高的预测精度和更好的泛化能力，能够更加准确地描述电力负荷的特性。

下一步可以扩大该网络模型的应用范围，如用于路径规划等优化问题。