基于LLSE的配电网状态估计器及优化方法
唐海国,刘海峰,朱吉然 ,张志丹,毛涛
(1. 国网湖南省电力公司电力科学研究院,长沙 410007; 2. 武汉东湖学院,武汉 430074)
0 引 言
国民经济的快速发展带动了电力需求的迅速增长,为了解决我国电能资源及负荷不协调的地理条件限制,近年来超高压远距离输电进入了快速发展阶段。由此也带来了无功补偿、绝缘保护、继电保护和运行维护等方面的困难[1-4]。利用可再生能源发电给负荷就近供电,以此降低输电损耗和提高供电安全性,是解决上述难题的一个新思路[5-6]。
分布式电源一般指安装在负荷附近、利用新能源或可再生能源的小型发电装置,如风电、光伏发电、生物质能发电等[7]。分布式电源的接入不仅不改变了原有的配网结构,便于安装运行;而且有利于改善配网的供电可靠性和电能质量[8-9]。但由于分布式电源的输出功率具有随机性和波动性,给传统的配电网状态估计带来困难。
传统配电网状态估计[10-11]是指对给定的系统结构及量测配置,在量测量具有误差的情况下,估计出系统各母线上的电压有效值和相角,及各支路潮流。由于考虑测量误差的存在,其要求量测量具有冗余性,需要较多的测量装置。本文设计了一种基于线性最小二乘法(Linear Least Square Estimate, LLSE)的实时电压状态估计器,在已知节点功率统计特性的情况下,仅少量电压测量装置,即可以较高精度估计全系统各节点电压有效值和相角。
本文首先利用三相电压降落计算建立配电网的电压估计模型,根据线性最小二乘法得到估计器的表达式。分析风电等功率预测误差较大电源接入配电网时对估计器性能的影响,建立了对监测装置位置进行优化的模型,给出了其决策变量、目标函数和约束条件,通过在IEEE 33节点配电网络中的仿真计算验证了本文估计器设计和优化方法的正确性和有效性。
1 三相状态估计器设计
1.1 区域电网节点电压计算
设树状三相配电网络节点集合为V={0, 1, 2,…,N},其中根节点为0号节点,且每个子节点比其父节点的编号大。设节点fi的子节点集合Cfi={i∈V|i>fi, (i,fi) ∈ε},其中ε为该配电网络的边集合。
忽略三相线路对地导纳,节点i与其父节点fi的三相电压关系为:
(1)

以a相为例,节点i与其父节点fi的电压差为:
(2)
设三相电压对称,相角互差120°,忽略电压降落横分量,由式(2)得到a相电压有效值之差为:
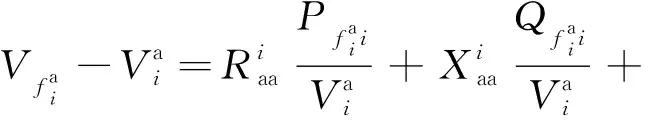

(3)

忽略配电网络线路功率损耗,得到:
(4)

设式(3)右边电压有效值为1.0 p.u.,得到:
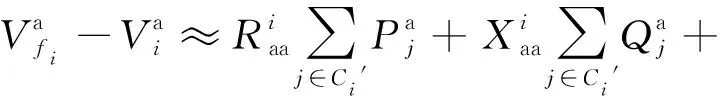
(5)
根据式(5),列写除根节点以外的其他N个节点与其父节点的a相电压有效值差表达式,写成矩阵形式有:
(6)

(7)

Pa∈N6N×6N的表达式为:
(8)
式中P∈NN×N是根据节点拓扑信息形成的矩阵,其表达式为:
(9)

S是功率矩阵,其形式为:
(10)
Pm∈NN×1和Qm∈NN×1是除根节点外的其余N个节点流出的m相有功和无功功率。
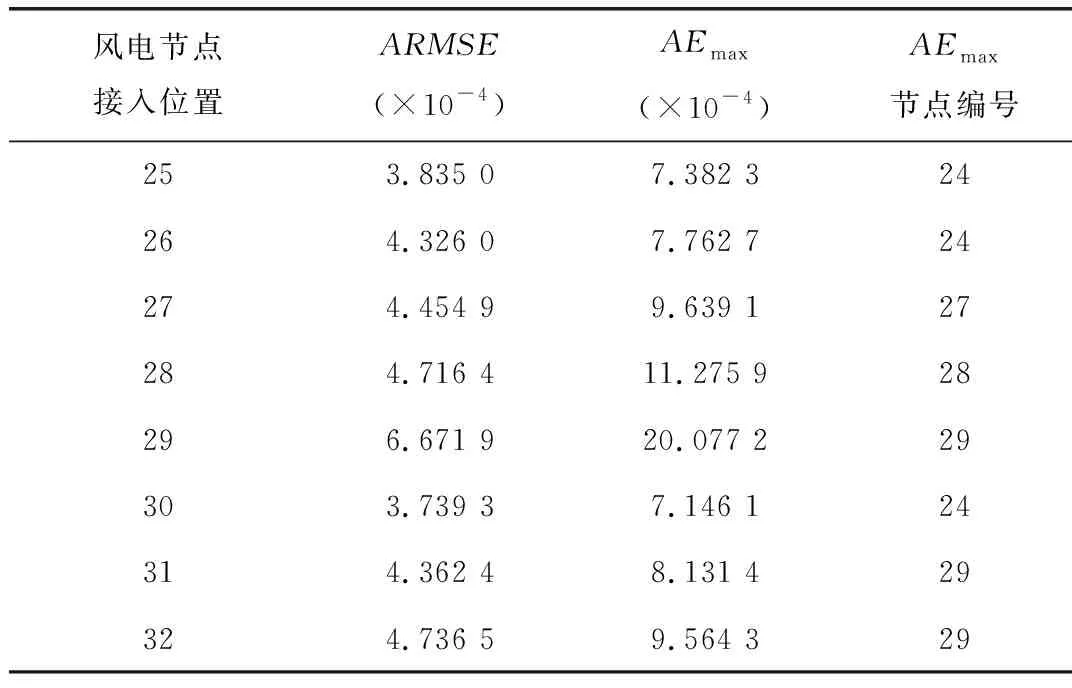
在包括根节点在内的M(M (11) 类似的,其余N-M+1个无测量装置节点的电压与根节点电压有效值之差可表达为: (12) (13) 可使均方误差最小。其中cov(·)是随机变量的协方差,var(·)是随机变量的方差。 (14) 同理,E(ΔVe)的表达式为: (15) 协方差cov(ΔVm,ΔVe)的表达式为: (16) (17) 将上述各变量的表达式代入式(13),得到: (18) 式(18)即为所设计的节点电压有效值的状态估计表达式,在已知每个节点功率的统计特性(均值和方差)时,根据电压测量装置提供的节点电压有效值信息,可以对未放置电压测量装置节点的电压有效值进行估计。 电压测量装置的位置不同,将对估计器精度产生很大影响,以电压测量装置位置作为决策变量, 可表示为: x=(x1,x2,…,xM) (19) 式中xi表示电压测量装置i所在的节点编号。 以a相电压为例,对具有N+1个节点(其中根节点编号为0)的树形配电网络,在其中M个节点(包括根节点)放置电压测量装置,用平均均方根误差(Average Root Mean Square Error, ARMSE)评价估计器的估计精度,ARMSE的表达式如下: (20) 以ARMSE作为目标函数,在给定电压测量装置数量时,当某一放置方案具有最小ARMSE时,认为此方案为最优放置位置。 在决策变量x中,不允许将两个电压测量装置放在同一节点,即: xi≠xj,(i≠j) (21) 放置电压测量装置节点的数量需小于总节点数量,得到: M≤N (22) 综上所述,状态估计器的优化模型可以表示为: (23) 本文利用MATLAB以如图1所示的IEEE 33节点配电系统为目标进行仿真计算,结果均以标幺值表示。 图1 EEE 33节点配电系统 设0号节点电压保持1.0 p.u.不变;对于一般的负荷节点,假设其流出有功功率和无功功率符合高斯分布N(μ,σ2),设σ=0.3μ;考虑分布式电源接入配电网络,对于光电节点,也可认为其发电功率符合高斯分布N(μ,σ2);而对于风电节点,用威尔分布双参数曲线[13]对风速进行统计描述,从而建立其发电功率的数学模型。 根据前推回代潮流计算[14]得到节点电压有效值的真值,估计器得到的结果作为节点电压有效值的估计值,以此计算ARMSE。 在给定的电压测量装置数量M的条件下,假设配电网络中所有节点的功率都符合高斯分布N(μ,σ2),其中σ=0.3μ;利用粒子群算[15]法求解优化模型,得到最优放置位置,如表1所示(结果均以标幺值表示)。 表1 不同电压测量装置数量下的最优放置位置 可以看出,当电压测量装置增加到一定数量时,节点编号为17、24和31的节点出现的次数很频繁,这是由于它们位于配电网络一段馈线的末端,而馈线末端附近节点的误差较大,需要放置电压测量装置以限制误差。 在测量装置放置在最优位置时,根据表1画出估计器的ARMSE随测量装置数量的变化曲线,如图2所示。 图2 ARMSE随电压测量装置数量变化曲线 可以看出,当电压测量装置的数量增加到7时,ARMSE的减小不明显,而在电压测量装置数量小于6个时,ARMSE随测量装置数量增加明显减小,故需找到一个合适的电压测量装置数量,以平衡估计器的高精度和经济性。 如前所述,当风电节点接入配电网络时,其发电功率特性不能用高斯分布来模拟。当测量装置数量给定(5个)且放置在最优位置(0,2,7,15,31)时,在配电网络的不同位置接入风电,用最大绝对误差(Absolute Error, AE)和ARMSE两个指标对估计器的性能进行评价。其中,最大绝对误差定义为: (24) 假设风电节点只有一个,且装设在节点编号为25-32的馈线段上,仿真结果如表2所示。 表2 风电节点接入下的ARMSE 可以看出,当配电网络中接入风电时,估计器的精度略有下降;且当风电节点接在25-32号节点中部时,风电节点对估计器的精度影响较大,这是由于中部节点离安装测量装置的节点较远,电压测量装置不能限制其误差;因此,要限制风电接入配电网给估计器精度带来的影响,需要在其附近安装电压测量装置。 本文提出了一种基于线性最小二乘法的区域配电网三相状态估计器,以解决电压测量装置数量有限和随机性分布式电源接入时的配电网状态估计问题。通过 IEEE 33节点配电网络中的仿真计算结果表明,配电网络线路末端附近节点的估计误差较大,需配置电压测量装置以提高估计精度;估计器的估计误差随电压测量装置数量的增加呈指数形式下降,存在饱和现象;风电节点接入配电网络时,估计器的估计精度下降,需在其附近安装电压测量装置以限制估计误差。


1.2 估计器表达式
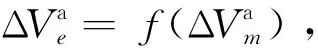



2 状态估计器的优化模型
2.1 决策变量
2.2 目标函数
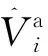
2.3 约束条件
3 仿真及性能分析

3.1 电压测量节点放置位置的优化


3.2 不同功率分布特性的优化
4 结束语

