改进ORB和Hough变换的指针式仪表识读方法

高建龙，郭 亮，吕耀宇，吴清文 ，母德强

1.中国科学院 长春光学精密机械与物理研究所 空间机器人工程中心，长春 130033

2.中国科学院大学，北京 100049

3.长春工业大学 机电工程学院，长春 130033

1 引言

指针式仪表因其结构简单、安装维护方便、可靠性高等优点在电力系统、石油化工等行业大量使用。以变电站系统为例，其中很多设备的工作状态需要通过仪表进行监测，如压力表，温度表等。然而在变电站系统的日常维护中，传统的人工巡检由于受工作环境高压高温、工作人员主观因素等影响，使得其存在安全性低，工作效率低，工作可靠性差等弊端。随着机器人和计算机视觉技术的不断进步，利用巡检机器人搭载摄像头进行视觉巡检大大提高了巡检工作的工作效率和可靠性。在通过视觉方法进行指针仪表读数方面，国内外科研工作者已经积累了丰富的经验。李伟[1]等人利用中心投影法求取指针角度以实现指针仪表的读数。杨志娟[2]等人利用模板特征获得仪表先验信息，并提出基于圆周区域的累积直方图法对指针进行定位，进而读取仪表示数。但中心投影法、模板特征法计算结果受图像噪声影响较大。李治玮[3]等人利用减影法通过模板图像与待测仪表图像相减计算指针位置。但是减影法只能简单有效适用于光照充足条件下的仪表指针定位，对于光照变化大、有阴影、图像背景复杂等情况，减影法会影响检测出的指针区域。李栋[4]、施健[5]等人利用添加圆心约束的Hough变换算法检测指针角度从而进行仪表的自动读数，但是在文中并没有明确给出圆心坐标的提取方法。李祖贺[6]等人结合指针质心，利用帧差法和角度法较好地实现了压力表的读数。

本文提出一种基于改进ORB和Hough变换算法的指针式仪表识读方法。通过改进ORB算法实现仪表的识别与透视变换矩阵的计算。利用图像预处理、投影法等方法进行指针的提取、定向。利用基于ORB特征匹配对的相似特征三角形法确定指针旋转圆心，运用添加圆心约束的Hough变换提取指针角度，并根据仪表的先验信息得到仪表读数结果。该方法流程图如图1所示。

图1 仪表识读方法流程图

2 仪表模板图像采集

为了准确识别指针式仪表，得到后续可靠的透视变换矩阵和定位指针旋转区域，首先要采集仪表的模板图像。采集模板图像时要求摄像头和表盘垂直在一条直线上。以一种压力表为例，采集其模板图像如图2所示。对模板图像进行处理得到仪表的先验信息，如表盘指针旋转圆心、半径、最大值、最小值等。其中，最重要的是指针角度与刻度之间的函数关系。图2仪表的指针角度与刻度之间的函数关系如下式：

图2 仪表模板图像

3 ORB算法及改进

ORB[7-8]算法是一种快速匹配算法，利用Oriented FAST检测算法检测图像上的特征点，再通过Rotated BRIEF描述符对特征点进行二进制向量描述，最后模板图像与采集图像的特征匹配采用汉明距离比值准则获得最终匹配结果。

3.1 特征提取

ORB算法采用计算效率高的FAST（Features from Accelerated Segment Test）角点检测算子实现图像特征点检测。针对FAST算子没有角点响应函数，并且具有很大的边缘响应的缺点，ORB算法采用Harris角点检测算法对特征点进行排序，再提取前n个点。Harris角点检测的排序依据的是Harris角点响应函数，如式（2）所示，其中M为描述像素点局部邻域内梯度分布的自相关矩阵，k一般取0.04，λ1、λ2为自相关矩阵的两个特征值。

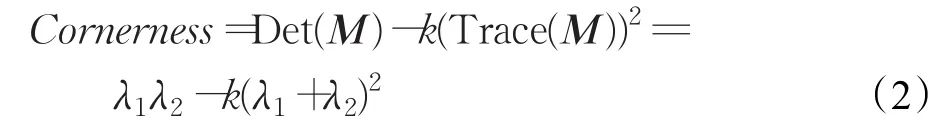
本文采用角点强化方法，通过选取λ1、λ2中的较小值λmin，与预先设定的阈值ε进行比较，若λmin＞ε，则保留该特征点。这种方式得到的特征点即为强化的角点，具有易于识别且稳定的特性，可以有效地去除分布密集的现象，剔除不稳定的边缘响应点，加强后续匹配的稳定性。

本文改进的FAST特征检测算法实现步骤如下：

（1）对预处理后的图像进行FAST角点检测，得到总个数为N的角点集S。

（2）对于集合S中的每个点进行角点强化，比较λmin与阈值ε的大小。当λmin＞ε时，保留该点为强角点，否则剔除。

（3）特征点数量阈值化处理。由于特征点数量过少会降低目标定位精度，过多则会增加冗余信息，降低处理速度。因此，采用特征点数量阈值化进行处理。考虑到后期仪表圆心定位至少需要8个特征点，取数量阈值n1=8,n2=100。当强角点数小于n1时，则返回1重新提取特征点；当强角点数大于n2时，则取排序后的前n2个特征点。

针对FAST检测的角点不具有方向信息，ORB算法应用灰度矩心法添加角点主方向。图像角点区域的灰度矩定义为：

其中，p,q决定了灰度矩的阶数。为了提高FAST角点的旋转不变性，x、y需满足x,y∈[ ]-r,r，r等于邻域半径。于是，可以得到灰度矩心为：

这样可构造角点中心O到矩心C的向量OC，则角点主方向为：

对于ORB算法不具有尺度不变性的问题，本文通过构造图像金字塔来加以补充。首先，利用高斯函数G(x ,y,σ)与图像函数F(x ,y)的卷积得到尺度函数：

利用高斯差分函数与图像函数卷积得到尺寸空间：

这样就可以得到一系列金字塔图像，同时应用改进的FAST角点检测算子可以得到不同尺度空间的特征点。于是，改进了ORB算法的尺度不变性。

3.2 特征描述

对添加主方向的角点，ORB应用Rotated BRIEF描述子进行描述。通过贪婪式搜索，并设置阈值，筛选向量点对相关性较低的描述子，得到最终描述子。

3.3 特征匹配

由以上方法获得的描述子为二进制比特串形式，ORB采用Hamming距离进行特征点匹配，即计算两个特征点的最近邻和次近邻距离，并与阈值比较来判断两者是否匹配。但这种方法匹配速度慢，出现错误匹配的频率高，影响程序运行效率和识别准确率。本文采用文献[9]提出的适合高维二进制特征的最近邻搜索算法FLANN进行粗匹配，并利用PROSAC[10]进行精匹配。最近邻距离采用汉明距离计算，如公式（8）所示：

式中，ai为模板图像任意角点的Rotated BRIEF描述向量中T(a0,a1,…,an)中第i位，bi为摄像机采集的待处理图像任意角点的Rotated BRIEF描述向量中C(b0,b1,…,bn)中第i位。假设模板图像中特征点k与待处理图像特征点中对应的最近邻和次近邻特征点分别为m,n，则汉明距离表示为Dkm、Dkn。于是，匹配比率为Dr=Dkm/Dkn。规定阈值Td=0.6，若Dr＜Td，则满足匹配要求，进行保留；否则舍弃。按照此方法得到FLANN匹配点对集。

采用FLANN匹配算法获得的匹配结果仍然会出现错误匹配的结果，于是利用PROSAC算法，根据特征匹配点对的相似程度对特征点进行排序，从中抽取相似度较高的样本估算出基础矩阵，并利用基础矩阵剔除误差较大的匹配。

3.4 透视变换矩阵计算

利用ORB特征匹配对计算模板图像与待处理图像的透视变换矩阵[11]。模板图像与待处理图像之间的关系如下：

其中，x、y分别为模板图像的行与列坐标，x′、y′分别为待处理图像的行与列坐标，H为3×3的透视变换矩阵。通过透视变换矩阵可以得到待处理图像中的仪表相对于模板图像中的仪表的偏转角度。

4 基于Hough变换的仪表读数

指针式仪表的一般特征是表盘背景与刻度、指针灰度差异较大，根据这一特点，本文通过对采集图像进行数学形态学处理、灰度拉伸、阈值分割等预处理。针对变电站仪表中指针顶部细、底部粗的特点，结合投影法判断指针方向，利用骨架算法细化指针，最后通过Hough变换法提取指针角度。结合偏转角度校正和函数关系式（1）即可得到最终的仪表读数。

4.1 指针提取

为了保证仪表读数的准确度，首先需要提取仪表指针，去除背景干扰。在采集仪表图像的过程中，由于光线、投影等干扰的影响，采集图像中会包含大量噪声。指针式仪表图像中的噪声大多服从高斯分布，因此可以选用高斯滤波器进行去除。首先，为提升图像质量、提取完整指针，利用5×5的高斯模板对仪表图像进行高斯滤波处理。

为了突出表盘区域，对高斯处理后的图像应用数学形态学处理。黑帽运算是闭运算的结果图与原图像的差，可以突出比原图轮廓周围的区域更暗的区域，从而可以有效地分离出表盘区域和指针。将黑帽运算后的图像转化为灰度图，然后利用灰度拉伸算法增强图像对比度，使后续指针提取更加可靠。

为了简单快速完整地提取指针的二值图像，最后结合直方图利用最大类间方差法（OSTU）[12]提取仪表指针二值图。OSTU算法将两个区域之间的方差最大化作为阈值选择准则。阈值计算公式如下式：

仪表所示真实值分别为0.82 MPa和1.77 MPa时，上述指针提取结果如图3所示。

图3 指针提取结果

4.2 指针定向

由于指针的形状特点，当指针处于水平位置时，将指针向图像横轴投影，则指针底部由于较粗在横轴上的投影值较大。由于指针式仪表的刻度呈现关于通过指针旋转圆心的垂直线对称分布的特点，因此可以通过投影法[13]判断指针底部所在垂直线的左侧或右侧来确定指针的所指方向。如图4所示为对应上述指针提取结果的指针向x轴投影的效果图。

在确定指针方向后，利用骨架细化算法[14-15]细化指针，以使后续Hough变化法提取指针角度更准确。骨架细化算法通过对8邻域的迭代计算去除指针多余的边缘像素，使细化的指针图像的连通性与原图像保持一致，细化指针线条宽度为单像素且为指针中心线。指针细化效果图如图5所示。

图4 指针向x轴投影图

图5 骨架细化的指针图

4.3 仪表读数

针对原始Hough变换算法计算量大、实时性差等缺点，本文通过圆心约束改善该算法的实时性与准确性。

在变电站各种各样的指针式仪表中，指针都具有一个共同的特征，即通过表盘圆心（或由指针旋转圆心起始）的具有一定长度的近似直线。因此在很多指针式仪表的识读研究中，都利用了指针旋转圆心这一特点来检测指针直线[4-5]。目前常用的提取圆形目标圆心的算法主要有极值均值法、Hough变换法和能量最小原理法[4]。但是在背景复杂环境情况下，难免存在圆形物体，因此利用Hough变换确定目标指针旋转圆心的方法可靠性较差；极值均值法在指针旋转圆心与表盘圆心不重合时不能满足指针旋转圆心要求。本文提出相似特征三角形方法确定目标指针旋转圆心，为Hough变换添加圆心约束。相似特征三角形方法原理如图6所示。具体方法如下：

首先在模板图像A中确定仪表的指针旋转圆心O。在利用上述ORB检测的模板图像的特征点集中，随机选取三个特征点P、Q、R，构成满足最小角大于5°的三角形，否则，重新选取特征点。在确定满足要求的特征三角形后，由圆心向任意两条边投影，投影点分别记为M、N。

图6 相似特征三角形方法原理图

在仪表待处理图像B的特征点集中，选取与模板图像P、Q、R编号相同，即相匹配的特征点记为P′、Q′、R′。这样，△PQR 与△P′Q′R′构成相似特征三角形。记O′、P′、Q′、R′坐标分别为，利用相似三角形性质可得目标指针旋转圆心在 △P′Q′R′对应边上的投影点 M′、N′的坐标：

由向量垂直关系可得待处理图像中关于目标指针旋转圆心O′的坐标的关系式如下：

利用式（14）便可以求得目标指针旋转圆心O′坐标。则k时刻目标指针旋转圆心在图像平面内的坐标位置 (uk,vk)，即

Hough变换原理中，一条直线的极坐标方程可以表示为：

ρ为原点到直线的垂直距离，θ为直线的法线方向与x轴的夹角。该方程表示笛卡尔空间对于一个给定点，对应极坐标平面上的一条正弦曲线。空间的多个点映射到极坐标平面就可以得到曲线簇。因此，空间中共线的点对应于极坐标中交于一点的曲线，只需确定极坐标平面中多条曲线的交点便能确定笛卡尔空间中对应的直线。Hough变换算法由于对每条曲线和点进行累计，所以运算量和耗时较大。改进的Hough变换通过添加检测的直线通过圆心的约束，即极坐标平面内指针直线对应的点限定在圆心对应的曲线上，这样大大减少了Hough变换的运算。如图7所示为指针直线检测结果。

由直线检测结果便可以得到指针偏转角度，结合透视变换进行仪表校正，将其带入由模板图像获得的指针偏转角度与刻度的函数关系式，便可以得到仪表最终读数结果。

图7 指针直线检测结果

5 实验结果与分析

为了验证本文指针式仪表识读算法的有效性和稳定性，实验环境如下：以0～2.5 MPa的指针式压力表为实验对象，实验平台如图8所示，采用内存4 GB，CPU主频2.40 GHz的计算机，利用C++和OpenCV视觉库在VS2012环境下编程实现，摄像机分辨率为640像素×480像素，安装在二自由度旋转云台上。该云台可以设计搭载在变电站巡检机器人上，以实现变电站的全自动巡检。

图8 指针式仪表识读实验环境

5.1 改进ORB算法实验

为验证本文改进ORB算法FAST特征点检测效果，分别对模板图像和待处理图像进行处理。图9为ORB算法中FAST角点检测结果，角点分布存在较严重的聚集现象，使错误匹配的概率提高。图10为本文改进的FAST角点检测结果，优化后的特征点检测具有稳定性好、分布相对分散均匀、不存在过于聚集等特点，为后续特征点匹配定位目标仪表和计算透视变换矩阵提供了稳定的特征点。

图9 FAST角点检测

图10 本文改进的FAST角点检测

为了验证本文改进ORB算法的可靠性，图11分别给出了本文算法与原始ORB特征匹配算法、传统SURF算法[16]在特征点数量阈值为200时的匹配效果对比图。表1为图11对应的每一帧的实验结果。

图11 不同特征匹配算法实验结果对比

表1 不同特征匹配算法实验数据对比

由图表数据对比可以看出，在检测的特征点数量一定时，本文算法检测到的特征点稳定，分布均匀，环境背景影响较小，正确匹配的特征点对较多，为后续获取指针旋转圆心和仪表读数提供了可靠的特征点匹配对。

5.2 指针旋转圆心提取

为了验证本文指针旋转圆心提取算法的准确性，分别进行了相似特征三角形法与文献[4]能量最小原理提取指针旋转圆心的对比实验，实验结果如表2所示，列出了指针旋转圆心在图像中的坐标为（395，298）时，相似特征三角形法与能量最小原理法确定圆心的实验数据。

由表2可以看出相似特征三角形方法确定圆心的平均偏差为3.696 pix，平均用时为53.725 ms，相比于能量最小原理方法识别准确度和速度分别提高了88.48%和88.08%，具有更高的准确度和实时性，能够为Hough变换提供可靠的圆心坐标限制条件。

表2 相同指针旋转圆心位置相似特征三角形法与文献[4]方法对比

5.3 仪表读数实验

首先采集实验中所用仪表的模板图像，并处理获得其先验信息。利用添加圆心约束的Hough变换方法获得指针角度，通过特征点匹配对得到的透视变换矩阵进行仪表偏转校正，再带入刻度与角度函数关系得到当前指针的读数。表3为原始Hough变换与本文改进算法的仪表读数实验结果。

表3 仪表读数实验结果

在实际工程应用中，指针角度的识别误差要求在3°以内，即对应于读数误差要求在±0.027 9 MPa范围内。由表3可知本文算法最大绝对偏差为0.01 MPa，比原始Hough变换算法准确度有了很大的提高，满足指针仪表自动读数的要求。

在算法实时性方面，利用相似特征三角形方法大大缩减了确定指针旋转圆心的时间，加上对ORB和Hough变换算法的改进，保证了本文算法的实时性。文献[5]没有说明仪表圆心确定的方法，因此本文考虑上述能量最小原理方法进行比较。两种方法对10幅待测仪表图像读数实验平均用时结果如表4。

表4 不同算法实时性比较 s

由表4可以看出，在保证仪表识读精度的前提下，本文算法较文献[5]方法用时降低了20.48%，能够满足仪表识读的要求。

6 结束语

本文利用改进的ORB特征匹配算法和添加圆心约束的Hough变换算法进行指针式仪表的识读。首先，对经典ORB算法进行了改进，使其检测的特征点分布更加均匀，使后续计算透视变换矩阵和Hough变换添加圆心约束更加可靠。然后利用图像预处理提取仪表指针，并通过骨架算法细化指针，利用投影法确定指针方向。最后利用基于ORB特征匹配对的相似特征三角形方法确定指针旋转圆心，并使Hough变换添加圆心约束，以提高检测指针角度的速度。实验结果表明，该方法能够实现指针式仪表的准确快速识读，满足变电站巡检的需求。