猫群优化算法求解柔性作业车间调度问题

姜天华

鲁东大学 交通学院，山东 烟台 264025

1 引言

柔性作业车间调度问题（Flexible Job Shop scheduling Problem，FJSP）是在经典作业车间调度问题的基础上发展而来的，它进一步考虑了工件柔性加工路径的特性，增加了车间调度的灵活性，但同时也给问题的求解带来了更大的难度[1]。对于该类问题的求解，目前智能优化算法已成为最受欢迎的方法之一，引起了国内外学者们广泛关注。

张超勇等[1]提出了一种具有双层子代产生模式的改进遗传算法，求解不同生产指标下的柔性作业车间调度问题。李修琳等[2]将蜂群算法和模拟退火算法相结合，提出了一种混合蜂群算法，求解柔性作业车间调度问题。仲于江等[3]将小生境技术引入到粒子群算法中，提出了一种小生境粒子群算法，求解多目标柔性作业车间调度问题。Ho和Tay[4]以工件最大完工时间为优化目标，提出了一种文化算法，求解柔性作业车间调度问题。Ennigrou和Ghédira[5]基于禁忌搜索算法提出了基于多智能体的方法求解柔性作业车间调度问题。Ziaee[6]提出了一种启发式方法优化柔性作业车间工件最大完工时间。随着各学科间的相互交叉和快速发展，不断涌现出更多新型的智能优化算法，但目前还没有一种算法能够获得所有问题的全局最优解，因此新型算法在生产调度问题的应用研究仍然是制造领域研究的热点。

基本猫群优化算法（Cat Swarm Optimization，CSO）是通过观察猫的行为习性而提出的一种群智能优化算法。它的主要特点体现在算法每次迭代时将猫群按比例划分为两个子群，并分别在搜寻模式和跟踪模式下进行个体位置更新，使算法能够同时进行全局和局部搜索[7]。目前该算法虽已被应用于多种复杂优化问题的求解，但在车间调度中的应用仍然较少[8-9]。因此，本文对基本猫群优化算法进行一系列设计和改进，提出了一种改进型猫群优化算法（Improved Cat Swarm Optimization，ICSO）求解柔性作业车间调度问题，以获得最优的工件最大完工时间。最后，通过基准算例验证了所提算法在求解FJSP问题方面的可行性和有效性。

2 柔性作业车间调度问题

车间内m台机器需要n个待加工工件，各工件相互独立，且每个工件i的加工由Ji(Ji≥1)道工序组成，各道工序可在多于一台的机器上加工，加工时间是由其所在机器的能力决定的。本文需要解决的FJSP问题是为工序分配合适机器，并确定机器上工序间的加工顺序，最终使工件最大完工时间最小。

对于该问题，考虑以下假设条件：

（1）工件和机器零时刻均为可用状态。

（2）同一时刻同台机器只可加工一道工序。

（3）工序加工时不可被中断。

（4）各工件加工优先级相同。

（5）不考虑机器故障和机器加工前的准备时间。

令Cmax表示工件最大完工时间，CiJi表示工件i的完工时间，则目标函数可表示为：

3 基本猫群优化算法

猫群优化算法的搜索模式可分为搜寻模式和跟踪模式两种，分别对应于全局搜索和局部搜索[7]。每次迭代过程时，首先按照一定比例对猫群个体划分成两个子群，然后对子群个体进行不同模式下的位置更新，直至算法结束。

在搜寻模式下，猫群个体需预先设定改变维数的个数和维数的改变范围，然后对原个体位置进行一定扰动，并填满搜寻记忆池，评价记忆池中新个体位置后，选择其中最优位置替代原个体位置[9]。在跟踪模式下，基本猫群优化算法与粒子群算法相似，采用速度-位移更新公式，并根据全局最优解的位置来更新猫群个体位置，如式（2）和（3）所示。

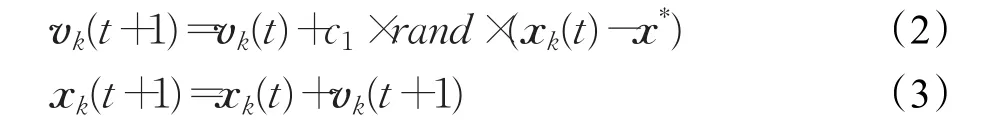
其中，t表示当前迭代次数；xk表示第k只猫的位置向量，x*表示猫群目前搜索到的最佳位置，vk表示第k只猫的速度向量，c1为加速度常数，rand表示[0，1]间的随机数。由于篇幅限制，基本猫群优化算法的步骤可详见文献[7]。

4 改进猫群优化算法

4.1 编码方法

个体位置采用前后等长的两段式编码，分别对应于机器分配和工序排序。个体位置中各元素均在[a,b]内任意取值，b＞a≥0，并根据一定的顺序存储。假设车间内包含3个待加工工件，每个工件具有2道工序，则个体位置向量总长度为12。若个体位置元素在[0，1]内任意取值，则编码方案如图1所示。

图1 个体位置编码

4.2 转换方法

基本CSO算法个体位置元素为连续值，然而调度解为离散值。因此，本文采用文献[10]中的转换方法，用于解决解空间与问题空间之间的相互转换。

（1）位置向量转换为调度方案

①机器分配段：根据式（4）将位置向量的元素转换成其所对应工序可选机器集合中机器的编号。其中，2 l为个体位置向量的总长度，s(k)为元素k所对应的工序的可选机器的数量，u(k)为已选机器在工序可选机器集合中的编号，即工序可选机器集合中第u(k)个元素为工序所分配的机器。

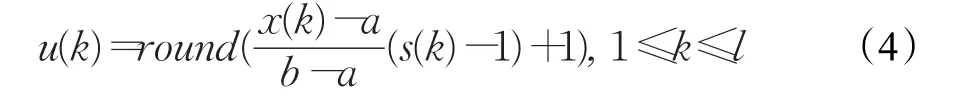
②工序排序段：首先对个体位置向量中的元素进行依次编号，然后采用升序排列规则，为每个元素赋予唯一一个的顺序值π(k)，将顺序值与位置编号进行对比，找到各顺序值对应的工序编号，从而确定工序加工顺序，如图2所示。

图2 位置向量转换成工序排序

（2）调度方案向位置向量转换

①机器分配段：按照文献[10]的转换方式，将工序所分配的机器编号转换成[0，1]中的个体位置元素，如式（5）所示。

②工序排序段：首先为排序方案中的元素进行依次编号，然后将工序编号和排序方案进行对比，从而获得顺序值π(k)，按照式（6）即可确定个体位置向量中各元素的值，如图3所示。

图3 工序排序转换成位置向量

4.3 种群初始化

分别针对调度解前后两段进行种群初始化，并按照4.2节中的方法将其转换为个体位置向量。

（1）前半段采用文献[11]中的启发式算法，即全局搜索、局部搜索与随机生成三种方式相结合来获得初始机器分配方案。

①全局搜索[11]：根据机器数建立一个等长的数组，各元素值为对应机器的负载。任选一个未分配机器的工件，并从被选工件第一道工序开始，将工序可选机器的加工时间与相应数组元素值相加，选择累加时间最短的机器作为工序的加工机器，然后更新数组元素值，将被选机器的加工时间加到数组对应元素上，依次类推直到当前工件的所有工序的加工机器均已选择完毕，然后再随机选择下一个未分配机器的工件，重复上述操作，直到所有工件分配完毕。

②局部搜索[11]：与全局搜索相比，主要区别在于该方法每次对工件进行机器选择后，数组元素值需要重新置零，且在执行过程中不存在随机选择工件。

③随机生成：在各工序可选机器集合任选一台机器加入初始调度解。

（2）后半段针对每一个已生成的机器分配方案，随机生成法获得若干个排序方案，评估每一个排序方案与机器分配方案的组合的适应度值，然后选择最优的组合作为一个初始调度解，重复上述过程，直到生成初始种群为止。

4.4 自适应行为模式选择方法

由基本猫群优化算法可知，猫群个体被以固定比例划分为两个子群，并分别在搜寻模式和跟踪模式下进行个体位置更新，即该算法在进化过程中执行全局搜索和局部搜索的个体数量的比例是固定的。然而，一个优秀的算法应该能够在进化过程中有效地协调全局搜索和局部搜索的能力，即算法在运行初期侧重于全局搜索，并在运行后期侧重于局部搜索。对此，本文采用自适应猫群行为模式选择方法，如式（7）所示，其中MR表示两种行为模式的混合比率，MRmax和MRmin分别表示混合比率的最大值和最小值，t表示算法当前迭代次数，tmax表示最大迭代次数。

4.5 搜寻模式

在基本猫群优化算法中，搜寻模式下参数的设置对算法性能具有较大影响，若参数设定过大，则解的变化范围较大，致使算法类似于随机搜索，不利于算法收敛；若参数设定过小，则解的变化范围较小，降低了算法的搜索能力，使其易于陷入局部最优解[9]。对此，采用文献[9]针对混流装配线排序问题，提出了一种基于多样化搜寻算子的改进搜寻模式。本文在此基础上根据柔性作业车间的特点重新设计三种不同类型的搜寻算子，各个体随机执行以下操作形成新个体位置来填满记忆池，选择其中最优个体位置替代原个体位置。

（1）N1：在工序排序部分中任选两个元素，并对所选元素进行交换操作，如图4所示。

图4 第一种邻域结构

（2）N2：在工序排序部分中任选两个元素，并将后一元素插入到前一元素之前的位置，如图5所示。

图5 第二种邻域结构

（3）N3：在机器分配部分任选一个元素（对应工序的可选机器应多于一台），然后将该工序分配至不同的机器上，并根据式（5）生成新的元素值。若图6中第4个元素被选中，其对应工序O22可选机器数s(4)为4，重新选择的机器在工序O22可选机器集合中的编号u(k)为2，则按式（5）生成的新元素值为0.33。

图6 第三种邻域结构

4.6 跟踪模式

在跟踪模式下，猫群优化算法与粒子群算法类似，二者均通过速度-位移公式更新个体位置，且同样易于陷入局部最优解。对此，本文在跟踪模式中引入莱维飞行策略，用于增强算法跳出局部最优位置的能力。莱维飞行是一种服从莱维分布的随机搜索路径，该搜索策略下短距离搜索与偶尔长距离行走同时存在，其中前者可使动物觅食时在自身附近小范围内进行精细搜索，后者则可使动物进入另一个搜索区域进行更广范围的搜索[12]。因此，莱维飞行策略已被许多学者引入到进化算法中，并且取得了较好的效果。文献[12]对莱维飞行和随机行走进行了仿真对比，即相同步数下，随机行走的搜索范围相对集中，而莱维飞行则具有更大的搜索范围和更强的搜索能力。文献[13]将莱维飞行嵌入粒子群算法的个体位置更新公式，使算法性能得到明显改善。因此，本文对猫群优化算法跟踪模式下个体位置更新方法进行了改进，利用服从莱维分布的随机数代替式（2）中服从均匀分布的随机数，从而使个体位置更新具有莱维飞行的特点，如式（8）所示。

4.7 跳跃机制

为了进一步改善算法的计算结果，在算法中引入跳跃机制，即为最优个体位置设置一个“解龄”，其初始值为零，若算法迭代一次后计算结果未发生变化，则解龄加1，否则置0。当解龄超过预设上限（文中取为10），则对当前最优个体位置执行变邻域搜索，迫使其跳出局部最优位置。变邻域搜索可直接利用本文第4.4节中三种搜寻算子作为邻域结构进行设计，具体步骤如下：

步骤1将当前最优个体位置作为变邻域搜索的初始解x，令ηmax←3，λ←1，并设置最大迭代次数λmax。

步骤2设置η←1。

步骤3 若η=1，则x′←N1(x)；若η=2，x′←N2(x)；若η=3，x′←N3(x)。

步骤4将x′作为初始解进行局部搜索，获取局部最优解x″。

步骤5 若 x″优于 x，则 x←x″，并令η←1；否则令η←η+1。

步骤6判断是否满足η＞ηmax。若是，令λ←λ+1，转到步骤7；否则，转到步骤3。

步骤7判断是否满足λ＞λmax。若是，转到步骤8；否则，转到步骤2。

步骤8变邻域搜索结束。

变邻域搜索中局部搜索则采用阈值接受法，具体步骤如下：

步骤1获取初始解 x′，并令阈值θ＞0，q←1，ϑ←1，设置最大迭代次数qmax。

步骤2 若 ϑ=1，则 x″←N1(x′)⋃N3(x′)；若 ϑ=0 ，x″←N2(x′)⋃N3(x′)。

步骤3 判断是否满足 Cmax(x″)-Cmax(x′)≤θ。若是，则 x′←x″；否则令

步骤4设置q←q+1，并判断是否满足q＞qmax。若是，x″←x′，转到步骤5；否则，转到步骤2。

步骤5局部搜索结束。

5 算例分析

本章对FJSP问题的基准Brandimarte算例[14]（MK01～MK10）和Kacem算例[15]（Kacem01～Kacem05）进行仿真并测试算法的计算性能。采用Fortran程序设计语言进行编程，并在WinXP系统下内存2 GB的Pentium CPU G2030@3.00 GHz，2.99 GHz计算机上运行。算法参数设置为：种群大小为200，最大迭代次数为500，记忆池大小为20，MRmax和MRmin分别为1.0和0.0，变邻域搜索和局部搜索最大迭代次数λmax和qmax均为10。

首先对引入莱维飞行策略和跳跃机制的有效性进行对比分析，将各算法在MK01～MK10算例下独立运行十次的结果进行比较，如表1所示，其中BEST表示十次运行获得最优值，AVG表示十次运行的平均值。CSO-1算法和CSO-2算法表示在ICSO算法中去除跳跃机制，其中CSO-1算法中跟踪模式个体位置更新按式（2）和式（3）进行，CSO-2算法跟踪模式个体位置更新按式（8）和式（3）进行，即引入莱维飞行策略。从表1中数据可以看出，ICSO算法的计算结果优于其他两种算法，验证了跳跃机制的有效性。此外，大多数情况下CSO-2算法的性能优于CSO-1算法，由此说明莱维飞行策略的引入能够改善算法的计算结果。

表1 三种算法的对比结果

为了进一步验证ICSO算法求解FJSP问题的有效性，将其与现有文献中的不同算法进行比较，对比结果如表2和表3所示。其中，粗体表示同一算例下各算法间的最优值，“—”表示对比文献中没有给出相应的计算结果。从表2和表3中的数据可以明显看出，ICSO算法在大多数情况下均能获得最优值。因此，ICSO算法求解本文FJSP问题具有一定的可行性和有效性。图7和图8分别为算例Kacem05和MK10的甘特图。

表2 Kacem算例对比结果

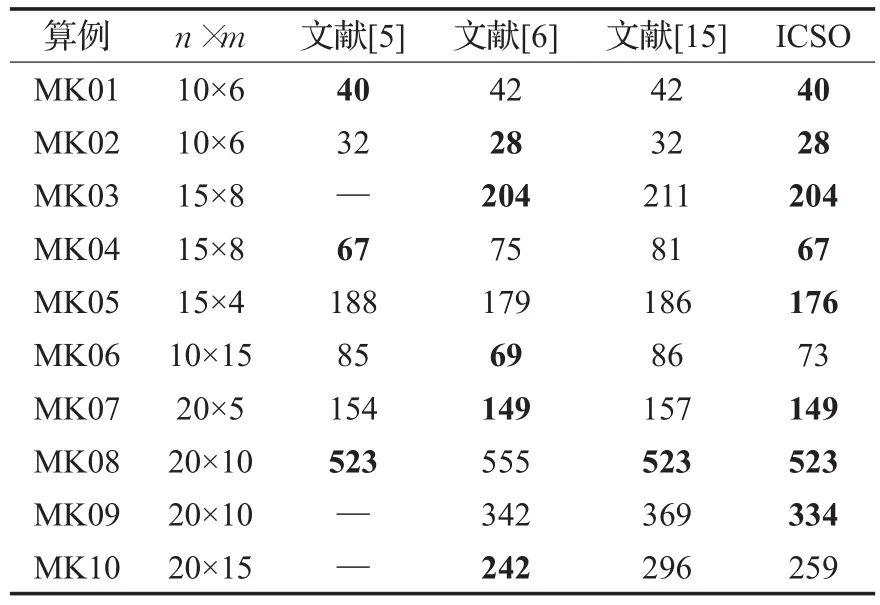
表3 Brandimarte算例对比结果

图7 算例Kacem05甘特图

6 结束语

本文以工件最大完工时间为优化目标求解柔性作业车间生产调度问题，提出了一种改进型猫群优化算法。

图8 算例MK10甘特图

（1）针对问题的特点，设计了两段式编码和基于启发式算法的种群初始化方法；采用自适应行为模式选择方法，使猫群个体执行不同模式下的个体位置更新；采用基于多样化搜寻算子的搜寻模式，并设计了三种不同搜寻算子；提出了基于莱维飞行的跟踪模式，增强了算法的局部搜索能力。此外，在算法中引入了跳跃机制，使算法性能得到了进一步改善。

（2）针对15个FJSP问题的基准算例进行算法测试，验证了算法莱维飞行和跳跃机制的有效性，并进一步验证了算法解决本文FJSP问题的有效性。

（3）下一步将把猫群优化算法扩展至更复杂的车间调度问题中，并结合问题的特点，设计出更加有效的算法。