基因沉默机制的基因表达式编程

郭 勇，张国锋，刘丽萍

1.黔南民族师范学院 计算机与信息学院，贵州 都匀 558000

2.黔南民族师范学院 生命科学与农学院，贵州 都匀 558000

1 引言

受生物界进化、学习、觅食等现象和行为的启发，衍生了众多的智能搜索算法，如遗传算法（Genetic Algorithm，GA）[1]、蚁群算法（Ant Colony Optimization，ACO）[2]、人工鱼群（Artificial Fish-Swarm Algorithm，AFSA）[3]、狼群算法（Wolf Pack Algorithm，WPA）[4]等，基因表达式编程（Gene Expression Programming，GEP）[5]是继GA之后受基因遗传理论启发的另一种智能搜索算法。公开GEP文献中大量使用形如的多项式函数进行实验佐证，实验表明多基因染色体GEP对多项式函数的挖掘具有较好的计算效果。在使用文献[6]中包含了正弦函数sin x、自然对数函数ln x、平方根函数Sqrt(x)等1目运算符的非多项式函数作为测试函数时，传统多基因染色体GEP的计算效果并不理想。为提升GEP对非多项式函数的挖掘能力，借鉴转基因工程中的基因沉默现象，定义新的多基因染色体结构，增加表达因子域，遵循“深度优先”原则对染色体中的基因进行连接解码，利用表达因子运算符的不同目数实现对染色体基因表达的抑制机制，通过遗传算子中基因转座算子和新的表达因子域突变算子，产生基因表达的位置效应，拓展出一种基因表达式编程算法——SFGEP（Gene Expression Programming of Symbol Field，SFGEP），SFGEP对包多种运算目数的非多项式函数的挖掘能力得到显著提升。

2 GEP与基因沉默简介

2.1 GEP简介

GEP以种群（Population）来模拟生命物种的遗传进化，种群由若干个体（individual）组成，个体抽象为染色体（Chromosome），染色体由1个或多个基因（gene）组成，基因编码字符集分操作符集F和终结符集T，基因的线性编码称为基因型，分为头部（head）和尾部（tail），头部编码取自F⋃T，尾部编码取自T，头部长度h和尾部长度t需满足关系式（1）。

式（1）中的M为运算操作符集F中的最大操作符目数。

基因编码按照“广度优先”原则构建的表达式树，称为表现型，对表现型表达式树后序遍历所得数学表达式称为基因解释。如F={+,-,*,/}和T={a,b}，头部长度为6的基因型编码“−+b*/aabbbabb”，其表现型表达式树如图1。

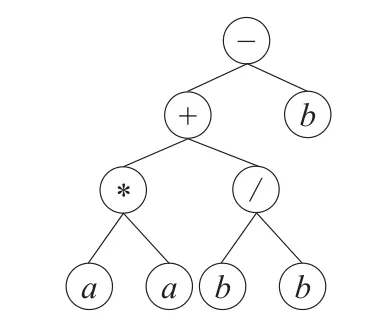
图1 表达式树

GEP通过选择、突变、转座、重组等遗传算子实现种群的进化，通过适应度及选择算子来控制种群演化方向。适应度函数可根据具体GEP问题进行设计，符号回归问题常用绝对误差、相对误差等统计函数作为适应度函数[7]：

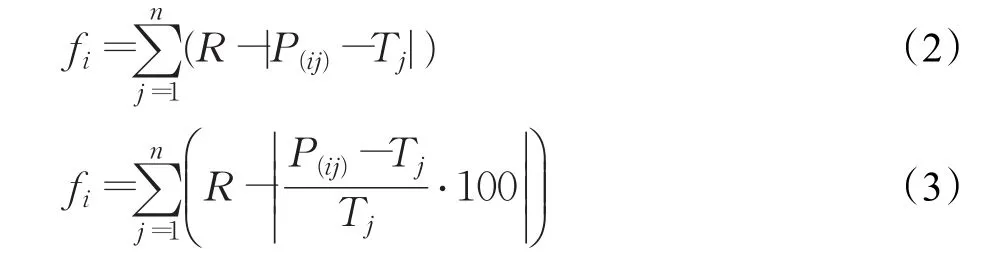
2.2 基因沉默

基因沉默（gene silencing）[8]指生物中特定基因由于种种原因不表达或者表达减少的现象，是基因表达调节的一种重要手段。基因沉默现象最早在植物转基因工程中受到关注，也称转基因失活。转基因沉默分为转录水平与转录后水平两种[9]，其中转录水平的转基因失活有两种情况，一种情况是导入的外源基因植入宿主基因组时，由于位置效应，外源DNA位于转录的不活跃区，产生转基因的异染色质化，从而出现不转录或者低水平转录。另一种情况是转基因反向重复区形成茎环结构，重复同源拷贝数增加，出现甲基转移酶异识别、甲基化，导致基因转录无法进行。

基因沉默的现象不仅存在转基因工程中，在生物界也存在类似现象。如植物抗病毒侵染的自然机制——病毒诱导的基因沉默（Virus-Induced Gene Silencing，VIGS），又如返祖遗传中祖先部分原有性状的基因仍然存在，长期的进化使其不具备活性而沉默，由于多基因调控等因素而激活。转基因沉默可以应用于植物抗病的基因工程和植物功能基因组研究。基因沉默和激活沉默基因的技术具有正反两方面的现实意义，一方面在保留优良性状的生物基因工程中需要克服基因沉默现象，使优良基因得以表达，或者对生物原有优势性状的沉默基因进行激活。另一方面可利用基因沉默屏蔽原有的病理基因或劣势基因的表达。

3 基因沉默机制的SFGEP

3.1 GEP的“随机性”和“冗余性”

“随机性”是自然界演化普遍存在的现象，GEP作为一种仿生智能搜索算法，GEP遗传算子的随机性，使较小规模的种群可演化出更多可能模式，赋予了种群搜索GEP问题解的能力，保持一定的“随机性”是智能搜索算法有效的基础。在GEP基因中存在类似位置效应而无法在GEP表现型中得以表达的编码区域——中性区域，视为GEP基因编码中的“冗余”现象，这种“冗余”因遗传算子的实施而带来更多演化结果的可能性。

传统多基因染色体GEP中，采用固定连接运算符进行多基因的连接解释，染色体结构中基因个数固定，且所有基因在染色体的解释中都得以表现激活，不具备“冗余”情况，也不具备某个基因不表达的“沉默”现象，演化的“随机性”较弱。

3.2 SFGEP的染色体编码结构

SFGEP基因编码字符集包含操作符集F和终结符集T。SFGEP染色体结构由表达因子域S和表达基因域G两部分组成，如图2所示，表达因子域S的编码全部或部分取自操作符集F，S的符号集记为F′。

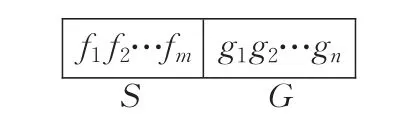
图2 SFGEP染色体结构

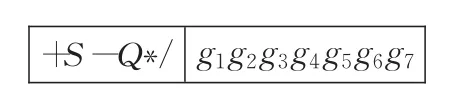
图3 SFGEP的染色体结构

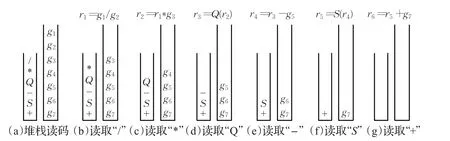
图4 SFGEP染色体的堆栈解释

图2 中 fi表示1个运算操作符，称为表达因子，gi表示单个基因，gi的编码结构与传统GEP相同。S中表达因子个数m与G中基因个数n的数量关系满足式（4）：

式（4）中的 M 为F的最大操作符目数。式（4）保证SFGEP解码有足够基因满足S中所有表达因子运算的需要，使SFGEP染色体的结构具备完备性。

3.3 SFGEP的遗传算子

SFGEP的遗传算子包括针对表达基因域与传统GEP相同的遗传算子：突变（单点、两点）、转座算子（IS、RIS）、基因转座算子、重组算子（单点、两点）。SFGEP增加了1种遗传算子：表达因子域S的突变算子，简称为S突变，即在表达因子域S中随机选择1个突变位，随机取F′中1个符号进行替换。

3.4 SFGEP染色体解释

（1）单个基因的解释

SFGEP表达基因域G中单个基因的解释与标准GEP相同，遵循“广度优先建树”、“后序遍历表达式树”等原则进行解释，基于“建树解释”算法时空复杂度高，可使用文献[10]等“无树解释”算法，提升基因解释效率。

（2）染色体基因的连接解释

SFGEP对G中基因采用文献[11]“深度优先”的堆栈解释方式，由于S中的表达因子运算目数可能不相同，基本原则是“每个表达因子 fi都要从基因栈中弹出至少1个基因”，当 fi(i＞1)运算目数为1时，不需要弹出的基因参与解释运算，则丢弃此基因，从而使此基因在解释中没有得到表达，成为“沉默基因”。

例1如图3所示的SFGEP染色体，表达因子域S部分的编码为6个运算操作符：+S－Q*/，表达基因域G包含7个基因，即关系式（4）取等号的情形。

例1中的SFGEP染色体基因连接堆栈解释过程如图4。图4（d）和（f）中由于表达因子Q和S的目数为1，不需要弹出的基因g4和g6参与运算，即g4和g6没有参与染色体的解释，形成基因沉默现象，显然沉默基因位受到了表达因子域中表达因子目数和位置的影响。

图4（g）中表达因子栈为空是染色体基因连接解释的终止条件。由于本例中表达基因域G基因个数取3.2节关系式（4）的“＝”情况，所以表达基因栈同时为空，若关系式（4）取“＞”，则基因栈中会存在冗余基因，这些冗余的基因与传统GEP基因的中性区域编码一样，可因“基因转座”算子等原因在演化中得以表达，形成另一种位置效应。例1表达因子域S对表达基因域G中的基因“激活”解释所得表现型如图5。

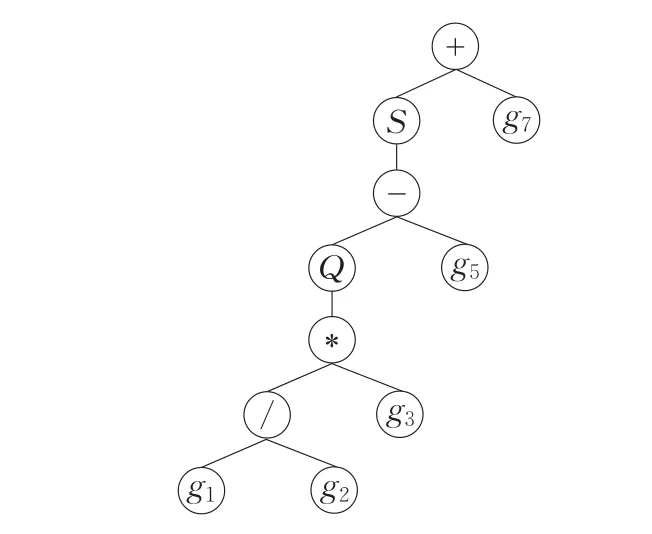
图5 SFGEP染色体基因的解释

4 对比实验与分析

本章以GEP公开文献及文献[6]中部分函数进行SFGEP与传统多基因染色体GEP函数挖掘的对比实验，实验一的表达因子符号集F′与操作符集F相等，统计标识为SFGEP-I，实验二限制表达因子符号集F′取F中部分符号，统计标识为SFGEP-II。

4.1 实验一

目标函数10个，其中前5个为公开文献中常用的多项式函数，后5个为包含了1目和2目运算符的函数，在对应取值范围内随机生成20组精度为10-16的训练样本。

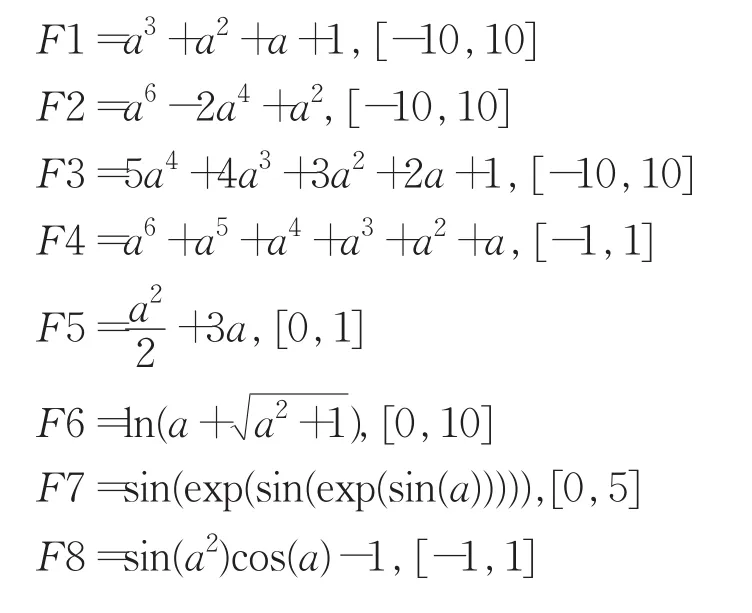
表达因子域长度取3，关系式（4）取“＝”，所以表达基因域由4个基因构成。传统多基因GEP染色体也由4个基因构成，采用“+”作为染色体基因连接运算符，函数F3的基因头部长度为15，其他函数的基因头部长度均为10，表达因子符号集F′=F。适应度函数采用反映训练样本集整体拟合度的统计函数R2：

其中m为样本数，yi为样本集第i个样本函数，y′i为染色体对i样本的解析值，yˉ为所有样本解析的平均值。

实验适应度控制阈值取0.999 9，S突变率为0.1，其他遗传算子参数设置如表1。

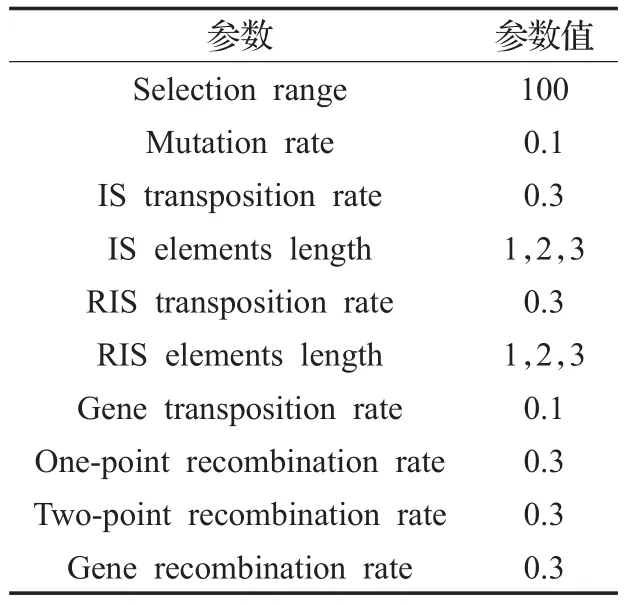
表1 遗传算子参数设置

演化种群大小为100个染色体，控制演化最大辈数为5 000辈，使用C#设计程序对每个目标函数分别使用SFGEP和GEP连续演化100次。实验统计项如表2。

（1）对于前5个多项式函数，传统GEP整体计算效果优于SFGEP，两者的成功率无显著差异。其原因主要在于本实验中GEP采用“+”作为多基因染色体的连接运算符，连接运算结果：g1+g2+g3+g4，形式上与多项式函数相近，GEP演化成功辈数的3项指标整体优于SFGEP。但由于“+”满足交换律，尽管传统GEP多基因的连接运算采用“广度优先”原则如图6（a），其运算结果与采用“深度优先”原则如图6（b）的结果相同，实验中的操作符集F均含有“+”，显然SFGEP的表达空间包含了GEP的表达空间，SFGEP随机演化搜索到最优解的概率相对较小，表现在平均成功辈数上SFGEP劣于传统GEP。

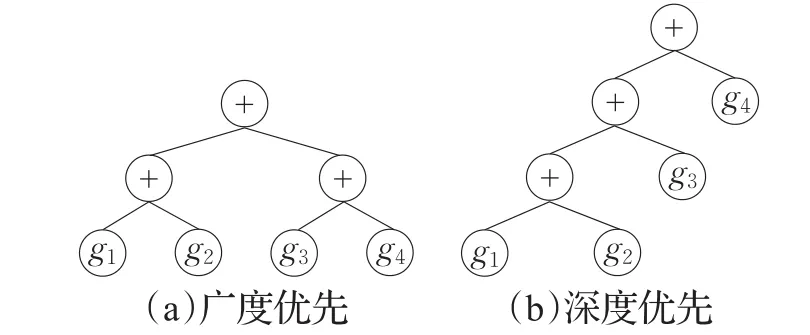
图6 多基因染色体连接解释

（2）对于后面5个包含有1目和2目操作符的非多项式函数，除了相对简单的函数F10外，其他略复杂的非多项式函数，SFGEP的整体计算效果明显优于传统GEP，主要体现在成功率方面。特别是在F7、F8、F9这三个函数的成功率上，SFGEP大幅领先于传统GEP。对于类似F10这样形式较简单的函数，SFGEP则不具备优势。

4.2 实验二

针对实验一中F10等函数的平均成功辈数较弱于传统GEP的结果，采取表达因子符号集F′取操作符集F的部分符号的措施再进行对比实验，即限制表达因子符号集F′的方法，并增加了以下五个目标函数：

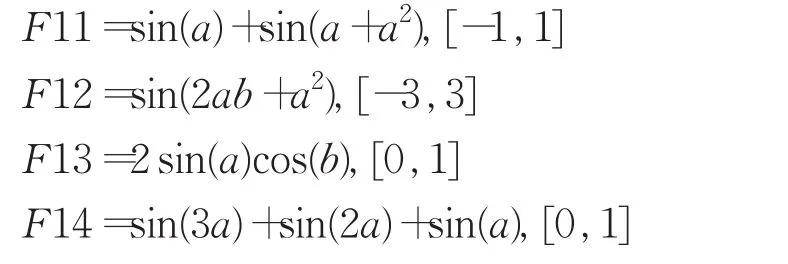
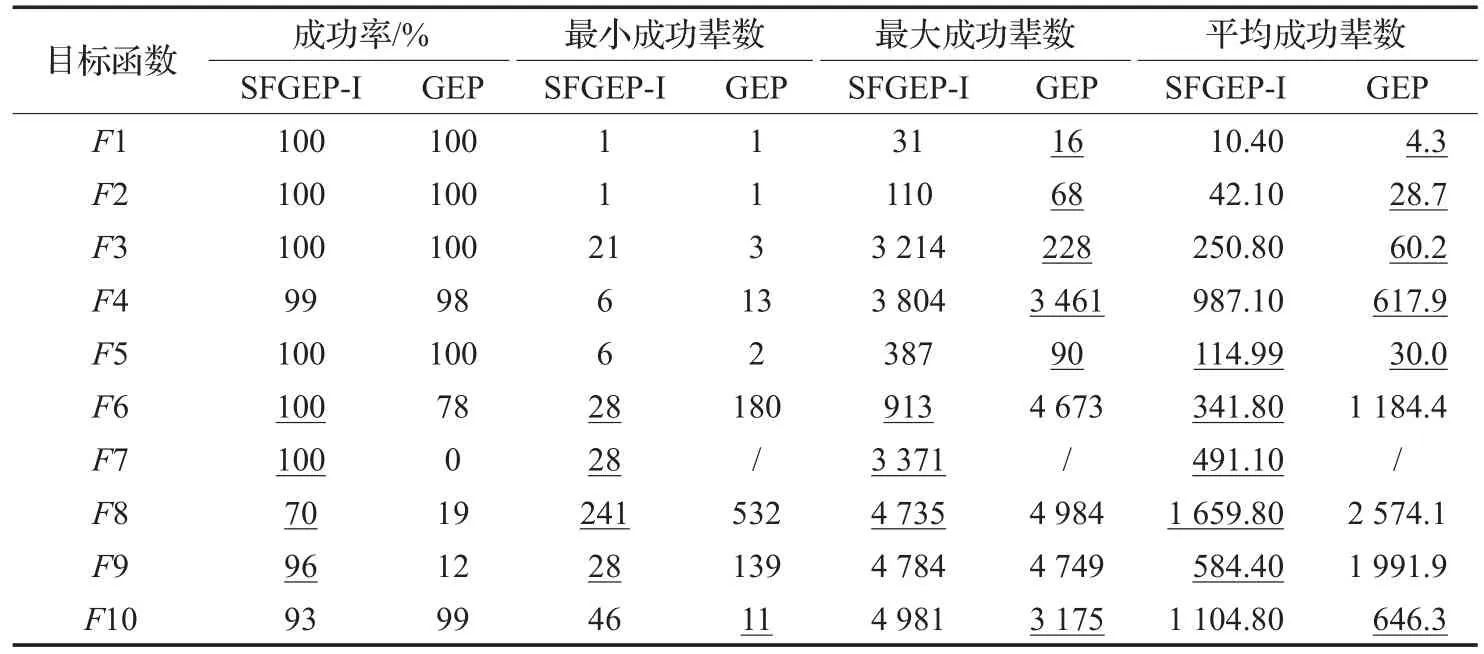
表2 实验一数据统计

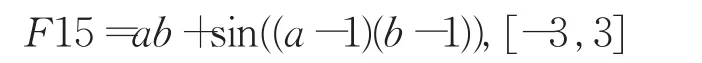
限制表达因子符号集F′的基本原则：（1）基于“+”与“－”、“*”与“/”的逆运算关系，二者取其一；（2）基于基本三角函数间的可换算关系，正弦函数、余弦函数、正切函数、余切函数四者取其一；（3）其他函数适当取舍，保持表达因子符号集F′至少包含2个符号。各目标函数的表达因子符号集F′如表3。

表3 实验二表达因子符号集F′设置

演化的其他设置与实验一相同，实验主要统计了SFGEP-II与传统GEP的成功率和平均成功辈数（四舍五入保留2位小数），成功率统计结果如表4。

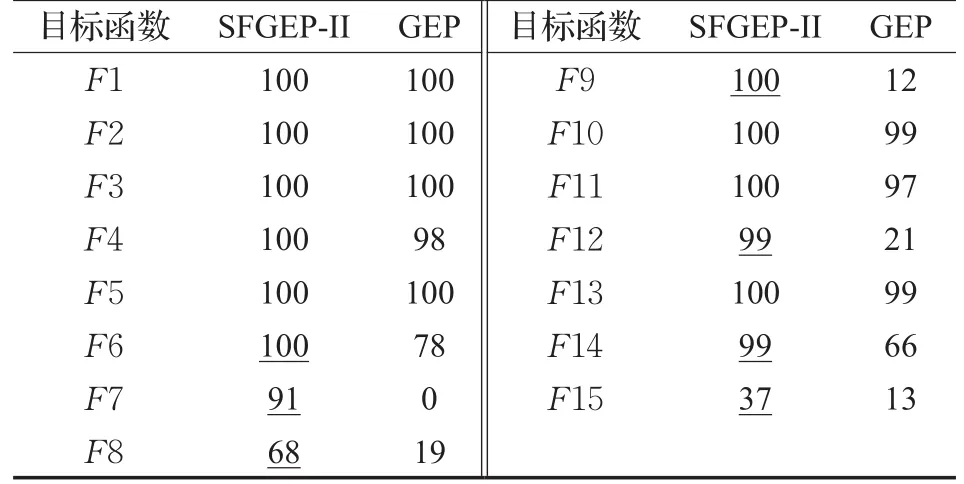
表4 实验二成功率统计%

表4数据表明，前5个多项式函数，SFGEP-II与GEP的成功率无显著差异。后10个非多项式函数SFGEP-II成功率整体比GEP高，7个带下划线的数据具有非常明显优势。平均成功辈数统计结果如图7。

图7（a）为多项式函数 F1～F5对比。SFGEP-II在平均成功辈数上与传统多基因染色体GEP仍有一定差距，但相较SFGEP-I来说差距大幅缩小，F1和F2基本无差异，F4反而是SFGEP-II的平均成功辈数更小。

图7（b）为非多项式函数F6～F15的对比。由于GEP对F7的成功率为0，因而没有列出。统计结果显示，SFGEP-II在平均成功辈数上都优于传统多基因染色体GEP，体现了SFGEP对非多项式函数的总体收敛速度更快。

图7（c）为非多项式函数的SFGEP-I与SFGEP-II的对比。除F7外，其余函数的SFGEP-II SFGEP-I的平均成功辈数小，这主要得益于适当的表达因子限制使SFGEP-II的表达空间有所缩减。

5 SFGEP效能分析

5.1 SFGEP的计算复杂度分析

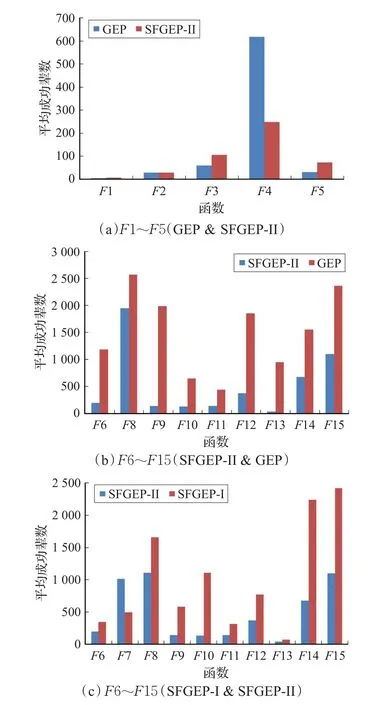
图7 实验二平均成功辈数统计

由于SFGEP染色体结构中包含了表达因子域S，在SFGEP染色体的基因个数取式（4）中的大于符号时，SFGEP的空间复杂度略高于传统多基因GEP，对巨大种群应用情景有一定影响，在没有突破硬件内存极限的应用环境中影响较小。

GEP的每代演化都要在样本集上对种群所有个体进行解码计算，其中染色体的每个基因的解码总耗时最多。对于符号回归问题，由于传统GEP一般采用运算目数为2的加号对染色体中多个基因进行连接解释，传统GEP多基因染色体中的所有基因都需要进行基因解码计算。SFGEP在进行染色体解释的过程中，可能因为表达因子S中存在运算目数为1的运算符，形成部分沉默基因，染色体解释不需要对这些沉默基因进行解码计算。尽管SFGEP演化中多了1个S突变算子，由于一般其突变率较小，每代演化仅进行1次S突变，而每代演化基因解码的计算量要大得多，加上多数符号回归问题只包含1目或2目运算符，染色体结构相近的SFGEP由于存在基因沉默现象，不需解码沉默基因，需要解码的基因总量相对传统GEP更少。所以，从整体演化计算过程来看，在种群规模相同，染色体结构基因数相近的情况下，SFGEP的计算时间复杂度不高于传统多基因染色体GEP。

传统多基因染色体GEP采用广度优先原则连接解释多基因染色体的方式，当不采用“+”（或“OR”）等具备交换律特性的连接符时，算法设计的时空复杂度较高，SFGEP采用深度优先原则连接解释多基因染色体，算法可使用时空复杂度更低的简单循环结构实现。

5.2 算法有效性分析

由于传统多基因染色体GEP采用固定连接符号“+”（或“OR”）进行基因连接运算，使得从染色体结构“模式”更接近于“多项式函数”，在多项式函数发现方面具有先天优势。SFGEP利用表达因子域中的多种符号进行基因的连接运算，染色体结构“模式”较接近于非多项式函数，虽在多项式函数发现上有一定弱势，但对第4章实验中的非多项式函数的发现有明显的优势。SFGEP既保持了对多项式函数的挖掘能力，同时具有良好的多种目数运算符、非多项式函数挖掘的效能。表达因子域的多操作符连接运算与“冗余”的基因域，使SFGEP可能包含更多形式的数学模型，从而带来更多的选择与可能，采用SFGEP有可能找到符合生产实际的数学模型，所以SFGEP具有一定的工程实践意义。

SFGEP对非多项式函数符号回归问题的有效性不仅因为“模式”上的优势，还来源于SFGEP采用深度优先原则连接多基因，相对于传统GEP的广度连接，SFGEP染色体的表现型表达式树更高，按照文献[12]基于表现型的GEP解空间模型理论，在更高的表现型子空间中等价的最优解接近于几何级数的增长趋势，相同基因数的染色体，SFGEP比传统GEP探索更高子空间的能力更强，根据文献[13-14]理论，随着演化代数的增加，种群中适应度更高的个体更多，SFGEP搜索到等价最优解的概率更大。

6 结束语

GEP给出了一种非二进制编码遗传进化算法的基本思想与计算框架，在此基础上许多GEP研究者针对解决不同类型问题和GEP效能的改进进行了GEP算法的拓展[15-20]，SFGEP给出了一种包含表达因子域的多基因染色体结构和“深度优先”、“多表达连接运算符”解释染色体的GEP拓展计算框架，为解决生产实践中的GEP问题提供了一种新计算方案的选择。今后将进一步对SFGEP的生产实践应用、染色体基因数对演化效果的影响及调控、表达空间模式及其多解特性等方面深入研究。