具有超线性收敛性的非线性半定规划的滤子算法
赵 奇, 张 燕
(江苏科技大学 张家港校区 基础教学部,张家港 215600)
非线性半定规划问题(nonlinear semidefinite programming,NLSDP)是目前优化研究的一个热点,在工程学上,很多地方需要计算上述NLSDP问题, 如稳定控制反馈模型[1-2]、桁架设计优化[3]、鲁棒优化问题[4-5]等.此外,该问题还是相关应用问题, 如线性矩阵不等式[6]、二阶锥规划问题[7]的基础.关于NLSDP问题, 已经有了一些有效的算法,如文献[8]中提出了惩罚/障碍方法, 解决了带线性矩阵不等式的凸半定规划问题.文献[9]中提出了增广拉格朗日函数方法, 并设计了该算法的PENNON 程序来解决 NLSDP和双线性矩阵不等式问题.文献[10]中提出了求解NLSDP的原始-对偶内点算法, 并分析了算法的全局和局部收敛性.文献[11]中将非线性规划中的序列二次规划方法推广到NLSDP, 提出了序列二次半定规划方法.文献[12-14]中将非线性规划的无惩罚型方法推广到非线性半定规划问题上去, 提出了滤子算法和可行上界控制方法.文中主要讨论一种针对NLSDP问题的滤子算法.该方法的思想来源于文献[15]中提出的解决非线性规划问题的线性搜索滤子算法,在非线性规划中,已经证明了该算法具有全局和局部收敛性质.文中分析非线性半定规划滤子算法局部收敛性,在严格互补松弛条件和带sigma项的强二阶充分条件下, 证明了算法产生的序列具有局部超线性收敛性.文献[16-17]中对半定规划局部收敛性质做了研究工作,然而,这些理论分析中默认步长因子为1.在实际计算中,步长因子不可能总为1,因此Maratos效应也会发生. Maratos效应指出, 对某些效益函数,超线性收敛步可能被拒绝,从而破坏算法的超线性收敛性,因此必须采用一些手段来克服它. 文中去掉了步长因子为1的默认假设,采用一种针对非线性半定规划的二阶校正技术, 利用该技术避免Maratos效应.需要指出的是由于半定约束的存在,以前非线性规划的技巧不可能直接推广.
求解二次半定规划子问题时, 往往用一个正定阵直接替代海塞阵近似,计算效果并不好, 文中在求解二次半定规划子问题时,从SDPT3软件包[18]的计算原理出发, 利用最优性条件的比较给出了拉格朗日乘子的表达形式,并将其应用于BFGS校正中. 最后, 通过一些实际问题的数值实验, 表明该算法是稳定而有效的, 验证了二阶校正步和BFGS公式的作用.
1 问题与算法
考虑如下形式的非线性半定规划问题:
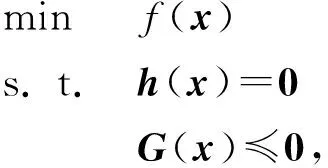
(1)
问题(1)中f:Rn→R,h:Rn→Rp,G:Rn→Sm都是光滑函数.Sm表示m×m实对称矩阵的线性空间. 文中矩阵内积定义为〈A,B〉=trace(AB),A,B∈Sm,Sm表示负半定偏序,即A≼B当且仅当A-B为负半定矩阵.
在当前迭代步, 求解如下形式的二次半定规划子问题:
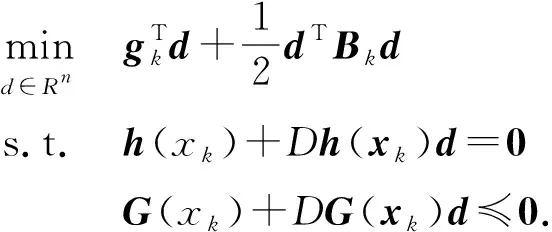
(2)
式中:gk=f(xk);Bk为含有问题(1) 的二阶导数信息的对称矩阵;Dh(x)为h(x)的Jacobi矩阵,线性算子DG(x)定义如下:
∀p∈Rn
其伴随算子DG(x)T定义如下:
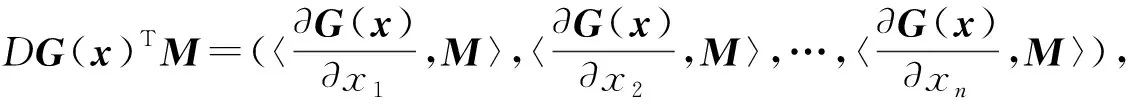
二阶算子D2G(x):Rn×Rn→Sm定义如下:
再定义线性化预测下降量:
和约束违反度函数:
v(x)=‖h(x)‖1+(λ1(G(x)))+
式中,λ1(A)为矩阵A的最大特征值, 且规定(α)+=max{0,α}.
如果下面的条件成立, 即
mk(α)<0, [-mk(α)]sf[α]1-sf>δ[v(xk)]sv
(3)
则步长因子α满足条件:
f(xk+αdk)-f(xk)≤ηfmk(α)
(4)
式中,sv>1,sf≥1,ηf∈(0,0.5),称满足条件(3~4)的迭代为f-型迭代. 否则,要求α沿着搜索方向dk使得约束违反度改善或目标函数下降两者之一成立, 即下面两个条件:
v(xk+αdk)≤(1-γv)v(xk),或者,
f(xk+αdk)≤f(xk)-γfv(xk)
(5)
至少有一个成立,式中γv,γf∈(0,1).
文中滤子集合定义为一个集合F⊆[0,+∞)×R;该集合为一个拒绝域,包含所有的在k个迭代步不能被接受的(v,f)点对.规定一个尝试步xk(α)=xk+αdk能够被滤子集合接受时,其对应的(v,f)点对不在拒绝域中,即(v(xk(α)),f(xk(α))∉Fk.
在开始时,定义F0={(v,f)∈R2:v>vmax},其中vmax>v(x0).在整个计算过程中, 当新的迭代步xk+1被接受后,如果不是f-型迭代,则滤子集合采用下面的公式进行更新:
Fk+1:=Fk∪{(v,f)∈R2:v≥(1-γv)v(xk),f≥f(xk)-γfv(xk)}
(6)
否则, 滤子集合保持不动,Fk+1:=Fk.
如果α太小,则认为算法做的线性搜索失败,定义临界步长因子:
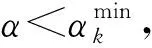
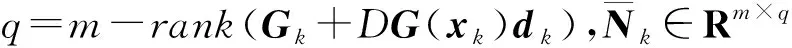
s.t.h(xk+dk)+Dh(xk)d=0,
(7)
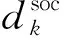
下面给出带二阶校正步的滤子算法:
步骤2:计算搜索方向.解子问题(2)来得到搜索方向dk.若(2)不相容,转步骤8.
步骤3: 检查中止条件.若‖dk‖≤ε,则停止.
步骤4: 线性搜索过程:
4.1: 令l:=0,αk,0:=1.
4.3: 若(v(xk(αk,l)),f(xk(αk,l))∈Fk, 则转步骤4.5.
4.4: 若式(3)成立,但式(4)不成立,则转步骤4.5;若(3)和(4)都成立,则转步骤5.
若式(3)不成立,式(5)中的条件至少有一个成立,则转步骤5;否则,若式(3)不成立,式(5)中的条件都不成立, 则转步骤4.5.
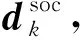
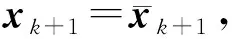
4.8:αk,l+1∈[T1αk,l,T2αk,l],l:=l+1,转步骤4.2.
步骤5: 更新迭代步:αk=αk,l,xk+1=xk+αkdk.
步骤6: 用式(6)更新滤子集合.
步骤7:k:=k+1.计算fk,hk,gk,Gk,Bk,vk,转步骤2.
步骤8: 可行性恢复阶段.计算新的迭代点xk+1,使得约束违反度v(x)满足v(xk+1)≤(1-γv)·v(xk).
更新滤子集合:
Fk+1:=Fk∪{(v,f)∈R2:v≥(1-γv)v(xk),f≥f(xk)-γfv(xk)},k:=k+1,转步骤2.
2 假设条件与算法收敛性结果
假设A:
A1: 函数f(x),h(x),G(x)是二次连续可微的.
A2: 存在紧凸集合Ω,使得对任意k,xk,xk+dk∈Ω.
A3: 存在两个常数0
A4: MFCQ约束规格[12]在任意可行点处成立.
定义下面的滤子更新指标集合A={k|Fk+1≠Fk},|A|表示其中元素个数,在假设条件A下,有下面的全局收敛性结果, 该定理证明的思想方法和文献[15]中的相似.
定理1:在假设条件A下,考虑由算法生成的序列{xk},则下面情况之一成立:
(1) |A|<+∞, {xk}的每个聚点都是问题(1)的KKT点.
(2) |A|=+∞, {xk}k∈A的每个聚点都是都是问题(1)的KKT点.
局部收敛性的分析除假设A外,还需要下面的假设B.其中B2,B3,B4详细解释参考文献[19], B5类似于文献[20]中假设.
假设B:
B1:xk→x*,其中x*是问题(1)的KKT点.
B2: 非退化条件在(x*,λ*,Y*)成立,其中(λ*,Y*)是相关的拉格郎日乘子.
B3: 严格互补条件成立,即
rank(G(x*))=r
rank(Y*)=m-r
B4: 带sigma项的二阶充分条件成立.
B5:‖(Wk-Bk)dk‖=o(‖dk‖),
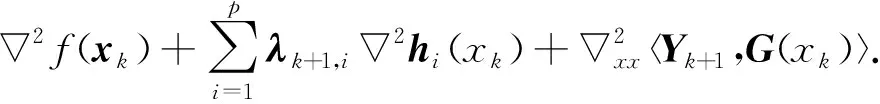
下面给出局部收敛性的主要结果:
首先, 给出二阶校正步的一些性质.这些性质的证明已经在文献[19]中给出.
引理2:在假设条件A和B下,有下面的结果成立:
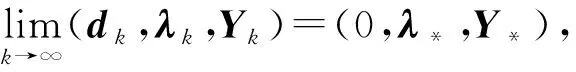
利用上面的结果和子问题(2)的最优性条件,可以推出下述结论.
引理3:在假设条件A和B下, 对充分大的k,若xk+1=xk+dk,则:
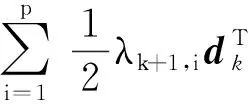
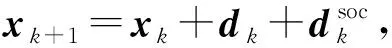
为了证明滤子算法的局部收敛性, 需要构造下面的一个罚函数作为证明工具, 即:
Pσ(x)=f(x)+σv(x)
和这个罚函数在Pσ(xk+d)的二次近似模型:
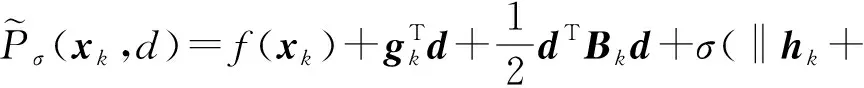
引入的罚函数仅仅作为证明的工具,而在算法中并没用到.同样利用引理2,和泰勒展开式, 可以得到下述结果.
引理4:在假设条件A,B下,若max{tr(Yk+1),‖λk+1‖∞}≤σ<+∞,则k充分大时,
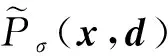
(8)
根据子问题(2)的KKT条件有:
gk+Bkdk+Dh(xk)Tλk+1+DG(xk)TYk+1=0
(9)
把式(9)两边和dk作内积, 结合dk的定义可得
(10)
注意到Yk+10,将下面的不等式:
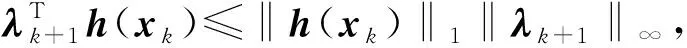
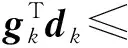
(11)
这样从式(8,11),结合假设A4,就得到:
(12)
因此第一个结果得证.
从文献[19] 中 引理 4.9 中的(4.41) 可知, 对充分大的k有
(13)
利用式(11,13)、引理2,以及假设A4可知, 对充分大的k有
(14)
(15)
因此, 从式(8,12,14)可得:
再结合式(15),可知:
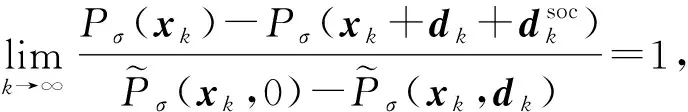
利用引理2,3,4的结果,结合文献[20]中引理4.5,4.6和定理4.7的证明,可以得到:
引理5:在假设条件A和B下,对充分大的k,总有:
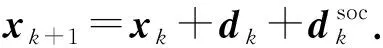
引理5意味着对充分大的k,全步长(步长因子为1)或者全步长带二阶校正步总能被接受.下面引理的证明和文献[17]中定理3.3的证明类似.
引理6:在假设条件A和B下, 对充分大的k,有下面的关系成立:
综合引理5和6的结果,可以推出下面的局部收敛结论:
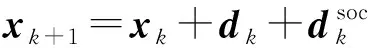
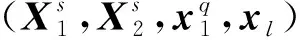
定理8:子问题(2)的乘子可以用下式得到:
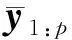
3 数值试验
为了测试算法的效果,在Intel(R) Core(TM) i5-3450, 16GB RAM 配置的电脑上进行数值试验. 用Matlab 2012a编写程序,子问题的求解采用
SDPT3软件包.Bk按照下面的公式进行校正:
qk=xL(xk+1,λk+1,Yk+1)-xL(xk,λk+1,Yk+1)
算法中使用下面的参数, 精度ε要求和文献[19]中的一样.
B0=I,γv=0.05,β1=0.9,β2=0.75,ν=2.1,δ=0.01,sf=5,sv=4.5,γα=0.8,ηf=0.001,T1=T2=0.6,ε=1.0e-4
测试问题1: 控制力反馈问题[13,22]

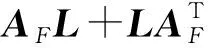
式中,QF=CTFTFC+I,AF=A+BFC.为方便和文献[20]中方法比较,初始点选择L=I,F=-0.1E,其中I为单位矩阵, 而E为元素都为1的矩阵.计算结果见表1.
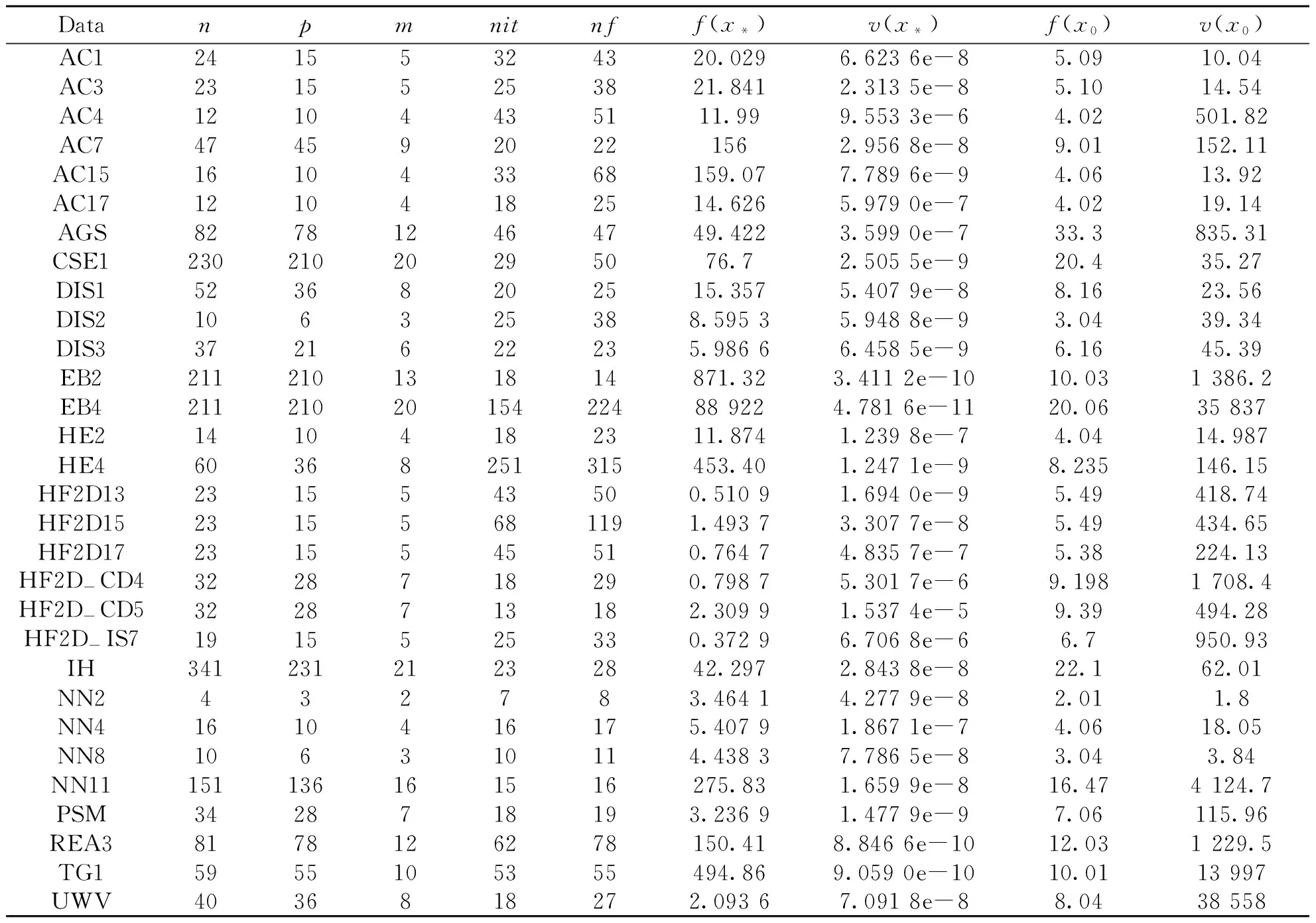
表1 SOFP问题测试结果Table 1 Results of SOFP
与文献[20]中无惩罚型方法相比,该算法总体效果较好,但考虑到滤子算法需要储存滤子集合的信息, 因此总体说来两种方法各有优劣.
通过改变初始点进行数值试验, 对AC4模型取初始点为L=I,F=O时,可以看出二阶校正步的效果.提高ε精度要求,分别对调用二阶校正步和不用二阶校正步做数值试验,明显前者计算效果较好,结果如表2.
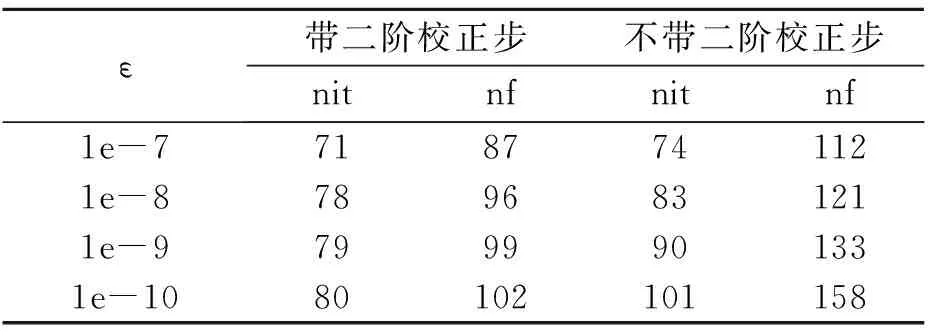
表2 二阶校正结果Table 2 Results of SOC
测试问题2:近端串扰问题[21]
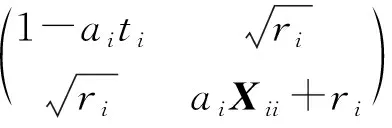
式中:ri,ai为区间[0,1]上随机数;参数P取1;初始变量Xii=ti=1,i=1,2,…,n.该测试问题说明定理8还原乘子后所得BFGS公式的效果. 该结果比较如图1.(a)使用了BFGS校正公式来更新,(b)用单位矩阵计算.明显看出使用了BFGS校正公式来更新后, 用很少的迭代次数, 函数曲线即趋向于稳定,而用单位矩阵则需要较多的迭代次数, 明显前者计算效果好.
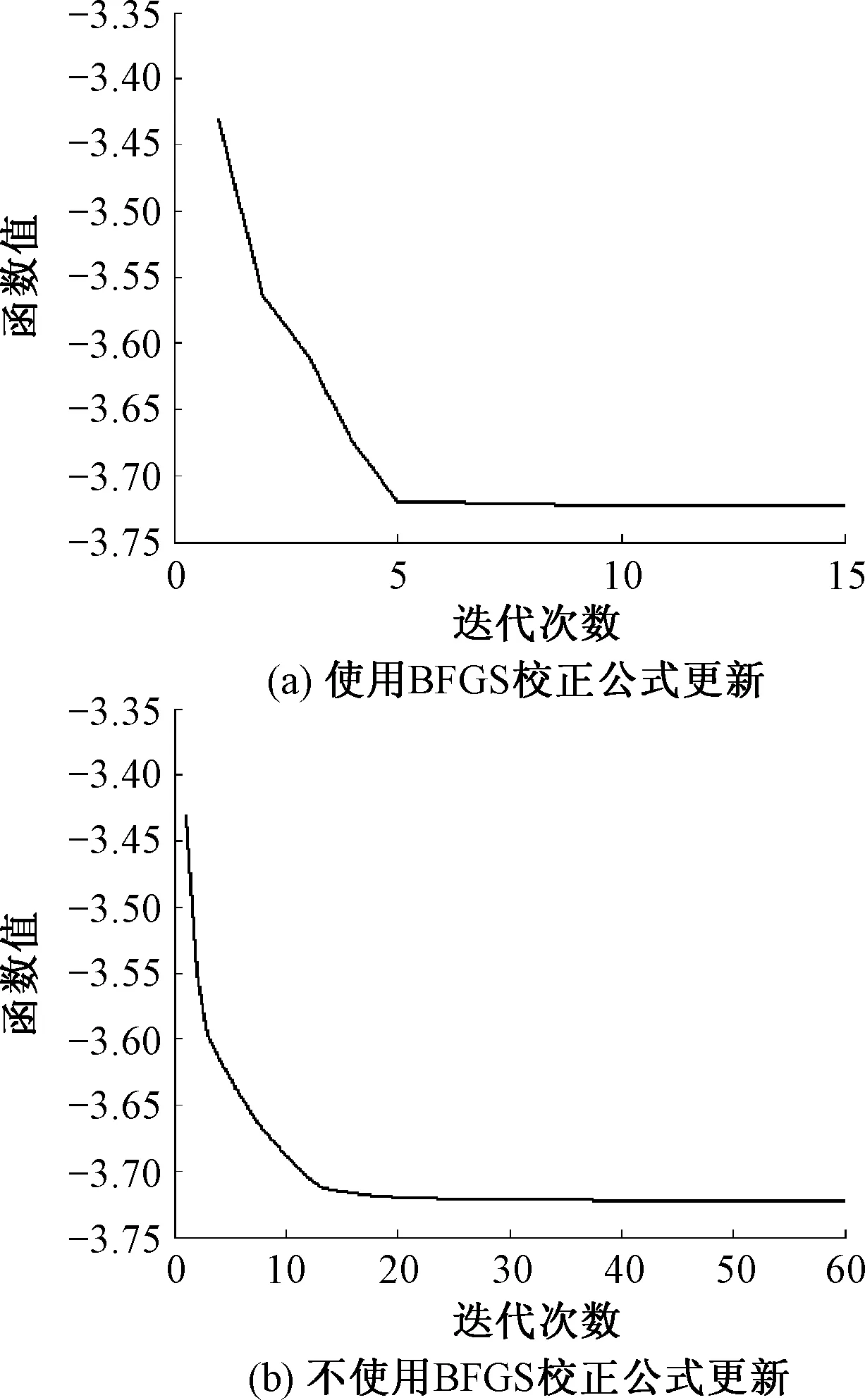
图1 使用BFGS公式的效果Fig.1 Results of using BFGS

