一类奇异非线性微分方程的正周期解

陈瑞鹏，李小亚

本文主要研究非线性微分方程

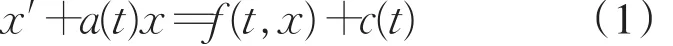
正周期解的存在性，其中a∈L1(ℝ/ωℤ;ℝ+)，c∈L1(ℝ/ωℤ;ℝ).非线性项f∈Car(ℝ/ωℤ×(0，∞)，ℝ)，即f|[0，ω]:[0，ω]×(0，∞)→ℝ 是 一 个L1-Carathéodory函数且在x=0处有奇性.作为一类重要的数学模型，方程（1）旨在描述与呼吸、心律失常及血细胞生成等密切相关的多种人体生理过程［1-3］.近年来，非线性微分方程（1）被诸多学者广泛研究［4-6］.同时，多位学者致力于研究该方程相应的微分系统，如 Ma［7］，Wang［8］和Chen［9］等.上述文献虽然都侧重于研究（1）及相应微分系统周期解的存在性，然而所涉及的非线性项大多不具有奇异性.据我们所知，对于奇异非线性微分方程（1）的周期解存在性的研究结果相对较少.可是，对奇异情形的研究无疑是极其必要的，所得结果将进一步丰富一阶周期微分方程和此类数学模型的相关理论.鉴于此，我们将为带奇异非线性项的方程（1）建立正周期解的存在性结果.

1 预备知识

本文总假设：（C1）a∈L1(ℝ;[0，+∞))为ω-周期函数且满足(0，∞)→ℝ 是L1-Carathéodory函数.

注1条件（C1）意味着线性方程x′+a(t)x=0是非共振的.此时相应的Green函数为G(t，s)=.此外，不难验证

引理1［10］（Schauder不动点定理）设K是Banach空间S中的一个有界闭凸集，A:K→K全连续，则A在K中必有不动点.

2 主要结果

对于函数ξ∈L1(0，ω)，记ξ∗和ξ∗分别为它的本性上界和本性下界.若ξ≥0，a.e.t∈[0，ω]且在一个正测集上严格为正，则记为ξ≻0.令

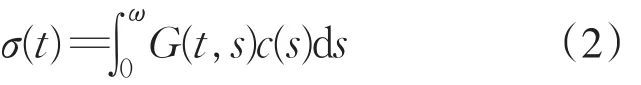
定理1 假设（C1）和（C2）成立且（C3）存在常 数α，β∈(0，∞)，m≤1≤M及 函 数b，e∈L1(0，ω):b，e≻0，使得0[0，ω].若σ∗＞0，则方程（1）存在一个正ω-周期解.

对于给定的x∈K，记I1={t∈ [0，ω]|r≤x(t)＜m} ，I2={t ∈[0，ω]|R≥x(t)＞M }，I3=[0，ω](I1⋃I2).任取x∈K，则由G(t，s)和非线性项f的非负性可得

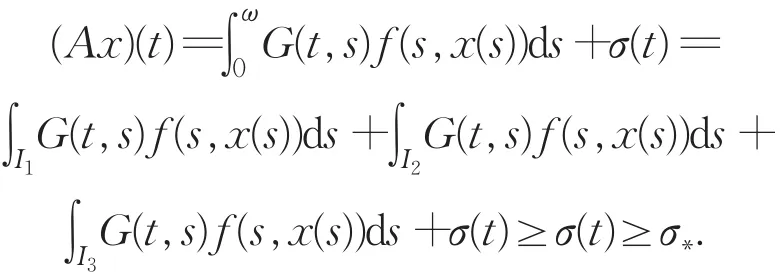
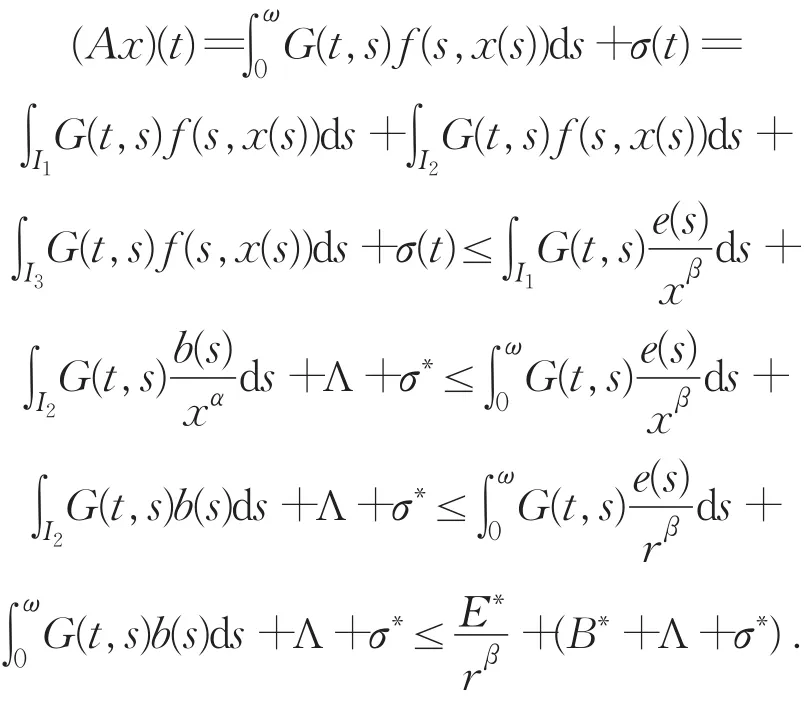
定理2 假设（C1）和（C2）成立且（C4）存在常数α，β，μ，ν∈(0，1)及满足b1，b2，e≻0 的函数x∈(0，1)，a.e.t∈[0，ω].若σ∗=0，则方程（1）存在一个正ω-周期解.

证明 方便起见，令δ=max{α，μ}，Bi(t)=定 义 闭 凸 集K={x∈Sω:r≤x(t)≤R，∀t∈[0，ω]，R＞1}， 其 中R，r是两个需要满足R＞r＞0和R＞1的待定常数

.由引理1可知，若A把有界闭凸集K映入自身，则A必有一个不动点，从而方程（1）必有一个正ω-周期解.

对给定的x∈K，记J1={t∈ [0，ω]|r≤x(t)＜1}，J2={t∈[0，ω]|R≥x(t)≥1}.任取x∈K，由条件（C4）可得

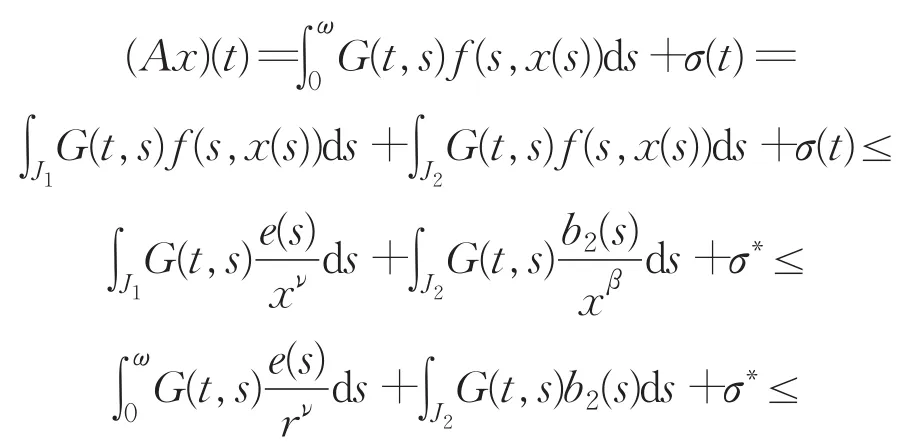
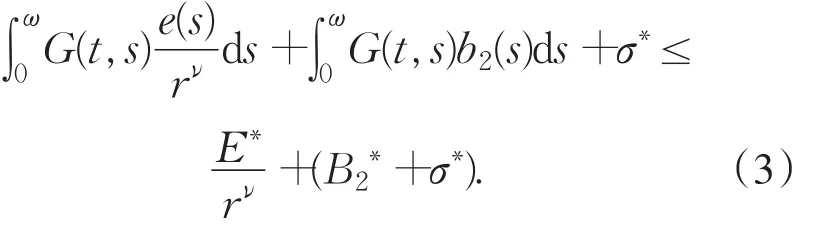
另一方面，对每个x∈K，有

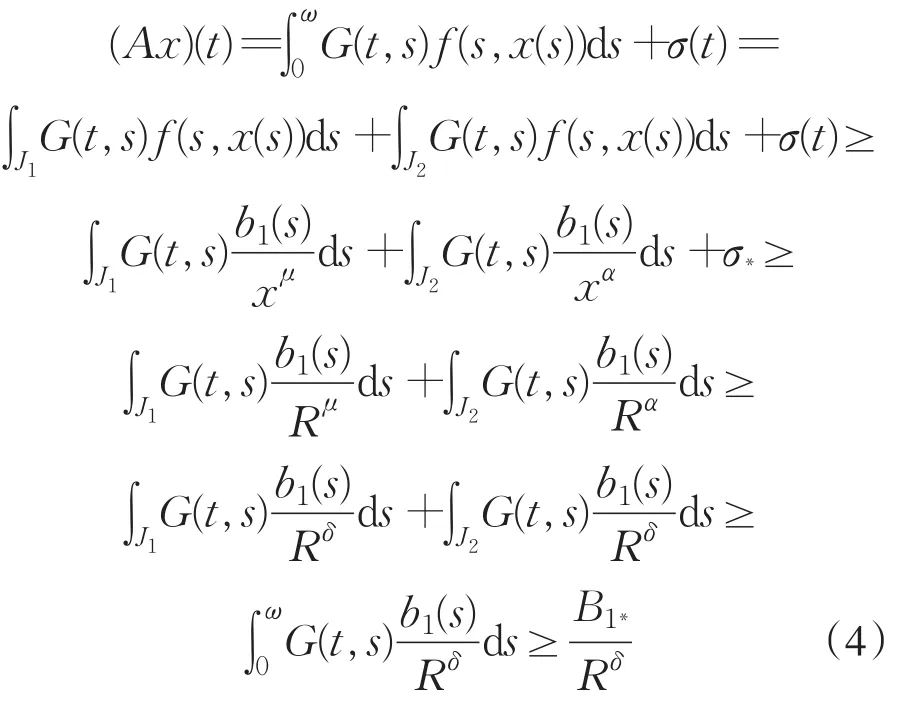
现在，只需确定待定常数R，r，使得

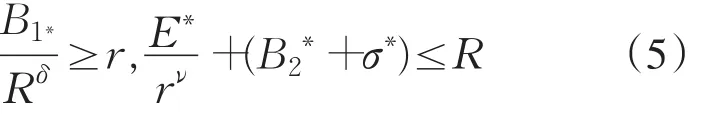
推论1 假设（C1）（C2）和（C4）成立，则非线性微分方程x′+a(t)x=f(t，x)存在一个正ω-周期解.

证明 由c(t)≡0结合（2）易得σ∗=0.从而由定理知结论显然成立.

3 结论

运用Schauder不动点定理，本文为一阶非线性微分方程x′+a(t)x=f(t，x)+c(t)建立了若干正周期解的存在性结果，对相关文献的已有结果进行了丰富和补充.以本文的工作为基础，今后还可以深入研究如下问题：

对于上述问题的研究，有助于进一步丰富一阶非线性微分方程与非线性微分系统的相关理论.