基于排队论的维修保障装备数量确定研究

吴同晗，陈春良，张仕新，丁 苹，刘 彦

(1.陆军装甲兵学院 装备保障与再制造系，北京 100072；2.陆军参谋部第2通信站指挥自动化站网络管理室，北京 101114)

维修保障装备是部队完成战时维修保障任务的物质基础，在维修保障力量体系中具有极为重要的地位。目前部队配属的维修保障装备在数量上存在冗余，其规模与作战力量极不适应。如何针对战时各种维修保障方式配备与作战力量规模相适应的维修保障装备数量已成为部队保障力量运用研究中急需解决的问题。目前分析维修保障装备数量需求的方法有很多。陈威利用模糊回归分析方法求出维修保障装备与维修能力满足度的相关函数[1]与求取维修任务和维修保障装备数量之间的解析关系式[2]两种思路,分别计算出维修保障装备数量并给出了示例分析。文献[3]从能力需求的角度出发对维修保障装备体系进行了分析并相应地运用IDEF0技术对上述分析进行了形式化描述，最终结合维修任务预测了维修保障装备的数量。但这些文献对于战时维修保障方式考虑的不够全面，所提出的维修保障装备数量确定方法也就不具备代表性，无法形成说服力。因此本文首先明确战时维修保障主要有伴随维修保障与定点维修保障两种形式，在此基础之上，借鉴排队论理论[4-6]分别对这两种维修保障形式进行分析并建立了不同的排队系统，根据该系统模型提供的信息，以装备完好率和受损装备等待维修时间为度量标准，对部队应配备的维修保障装备数量进行计算，从而能够有效地提高维修保障装备的工作效率，为部队维修保障力量体系规模设计奠定基础。

1 维修保障装备数量确定总体思路

由于不同的维修保障装备运用的场合不同，有的运用在伴随保障力量中实施现地抢救及抢修工作，有的运用在固定修理点对来往的作战力量进行定点维修及保养工作。为计算出合理的维修保障装备数量，运用排队论方法分别对定点维修保障和伴随维修保障两种维修保障方式进行分析，并以作战装备数量、作战装备故障率及故障装备平均修复率为输入条件建立排队系统。根据保障形式的不同以及作战力量对维修保障装备的不同任务需求，在计算维修保障装备数量时，对战时抢救抢修的排队系统以作战装备完好率为度量标准，而对战时抢救抢修的排队系统则以受损装备等待时间为度量标准，并分别对这两个度量标准进行计算。最后代入不同数值的维修保障装备数量，即可得到最佳的维修保障装备数量值。维修保障装备数量确定思路模型如图1所示。

2 排队系统的建立

2.1 排队系统的假设

战时维修保障装备主要对损坏的作战装备进行修复性维修，产生待修装备的时机与数量没有规律。为方便研究，本文假设所有类型的维修保障装备在进行修复性维修工作皆满足以下4个条件：

1) 发生损坏的作战装备数量仅与某时段的长短有关，而与这一时段的起始时刻无关。

2) 在足够小的时间段内，仅可能产生最多1台损坏装备，不可能产生多台损坏装备。可按下式表示：

(1)

式(1)中，p(t)为t时间段内产生2台或以上的损坏装备的概率。

3) 损坏装备的数量与不同时间间隔无关，即认为装备损坏是相互独立的。

4) 任意时间段产生损坏装备的概率之和为1，装备损坏数量满足有限性，即：

根据巴尔姆-欣极限定理相关内容[7]：若能保证每个相互独立的小强度流是平稳有序的，则足够多的这些小强度流之和近似满足Passion输入。因此我们可以认为，在时间段t内产生y台损坏装备的概率近似服从强度为λ的Passion分布，其表达式为：

(2)

确定时间段t内产生y台损坏装备的概率后即可通过相关分析确定对应维修保障装备的数量。

由式(2)可知，在[0,t]时间段内，没有产生任何作战损坏装备的概率为：

P0(t)=e-λt

(3)

因此出现至少1台损坏装备的概率为：

FTt=1-P0(t)=1-e-λt,t>0

(4)

其概率密度为：

(5)

因此可以确定产生受损装备的间隔时间服从参数为λ的指数分布。

根据现有数据统计可知，对产生损坏的作战装备修复时间服从参数为μ的指数分布，假设各维修保障装备服务于损坏的作战装备的平均时间相同且相互独立，则在[0,t]时间段内完成服务的概率为：

M(t)=1-e-μt,t>0

(6)

2.2 伴随维修保障的排队系统建立

伴随维修保障的排队系统是指：作战力量附属维修保障力量在战时运用多种发挥抢救抢修功能的维修保障装备对若干受损装备或淤陷装备同时进行维修保障工作的系统。该系统模型中作战装备的数量是有限的，属于有限源模型。假设某种维修保障装备数量为C，某一类作战装备数量为Y(Y>C)，且维修保障装备服务于同类别作战装备时，技术条件相同，则根据Kendall-Lee的符号表示方法[8]，可以将上述排队系统表示为：

M/M/C/∞/Y/FCFS

其中，FCFS表示先到先服务的服务规则。

设作战装备故障率为λ(台/小时)，修复率为μ(台/小时)，则可以确定该种维修保障装备的工作强度为：

(7)

记受损装备数量为X，则维修保障装备空闲概率为：

(8)

X台作战装备受损的概率为：

当1≤X≤C时，有：

(9)

当C+1≤X≤Y时，有：

(10)

受损装备的平均数量为：

(11)

排队待修的受损装备数量为：

(12)

战时的伴随维修保障主要是以尽可能少的时间恢复受损作战装备效能，使之重新投入战斗中，因此需要引入装备完好率这一指标，得到能够保证完好的作战装备数量最多时所需配备的维修保障装备数量。

装备完好率的计算公式为：

(13)

2.3 定点维修保障的排队系统建立

定点维修的排队系统是指在修理任务比较集中的区域开展定点保障的系统。在该系统中，可认为排队等待服务的作战装备数量无限制，符合“先到先修理”的服务规则，因此上述排队系统表示为：

M/M/C/∞/∞/FCFS

战时的定点维修排队系统基本处于多服务台并行工作的状态，其又可分为集中配置和分散配置两种情况，但经验证可确定集中配置相对于分散配置而言工作效率更高，因此本文仅考虑集中配置情况下的定点维修。

设作战装备故障率为λ(台/小时)，平均修复率为μ(台/小时)，则可以确定当有C台维修保障装备进行集中保障时其工作强度为：

ω′=λ/(Cμ)

(14)

记受损装备数量为X，则维修保障装备空闲概率为：

(15)

排队待修的受损装备数量为：

(16)

战时定点维修保障主要体现了所有待服务的受损装备向指定地点集结的特点，这时就需要决策者配备合理的维修保障数量，避免排队的队伍过长造成拥堵，不利于维修保障工作的开展。因此在定点维修保障这一情况中，引入受损装备等待维修时间这一指标，基于此计算合理的维修保障装备数量，减少排队队列长度，提高维修保障装备的工作效率。

受损装备等待维修时间为：

(17)

3 示例分析

某作战分队拥有轮式装甲装备20台，由轮式装甲抢救车、轮式装甲抢修车和保养车负责对其进行维修保障；轻武器设备10台，由轻武器设备抢修车和保养车负责对其进行维修保障。已知轮式装甲装备和轻武器设备的初始参数如表1所示。假设所有装备全部参战，则求所应配备的各类维修保障装备的数量。

表1 作战装备初始参数

3.1 伴随维修保障的模型求解

战时负责对轮式装甲装备进行伴随维修保障的装备为轮式装甲抢救车和轮式装甲抢修车；对轻武器设备进行伴随维修保障的装备为轻武器设备抢修车。以轮式装甲装备配备的维修保障装备数量为例进行计算。为方便研究，可将1台轮式装甲抢救车和1台轮式装甲抢修车的组合视为1个维修保障装备单元。根据式(7)—式(13)，可计算出取不同维修保障装备单元数量时轮式装甲装备的完好率，如表2所示。

表2 轮式装甲装备完好率

由此得到轮式装甲装备对应的维修保障装备单元数量与装备完好率之间的关系如图2所示。

对图2进行分析，可以看出随着维修保障装备单元数量的变化，轮式装甲装备完好率的变化呈先递增再递减最后平稳的趋势，若以装备完好率为评判依据，则当维修保障装备单元数为8个时，轮式装甲装备的完好率最高(87.3%)，应注意的是，例中轮式装甲装备数量为20台，则可计算出其完好数量为20×87.3%=17.46≈17(根据实际情况向下取整)。基于此考虑，根据表2相关数据，当单元数量取7时，轮式装甲装备完好数量也为16台，因此可最终确定轮式装甲装备维修保障装备单元数量应取8个。

依然按照上述思路可将轻武器设备的维修保障装备单元数量确定为5个。

因此，伴随维修保障时所需轮式装甲抢救车8台，轮式装甲抢修车8台，轻武器设备抢修车5台。

3.2 定点维修保障的模型求解

战时负责对轮式装甲装备进行定点维修保障的装备为轮式装甲抢修车和保养车；对轻武器设备进行定点维修保障的装备为轻武器设备抢修车和保养车。仍以轮式装甲装备配备的维修保障装备数量为例进行计算，将1台轮式装甲抢修车和1台保养车的组合视为1个维修保障装备单元。根据式(14)—式(17)，可计算出取不同维修保障装备单元数量时受损轮式装甲装备的等待维修时间(Wq0)，如表3所示。

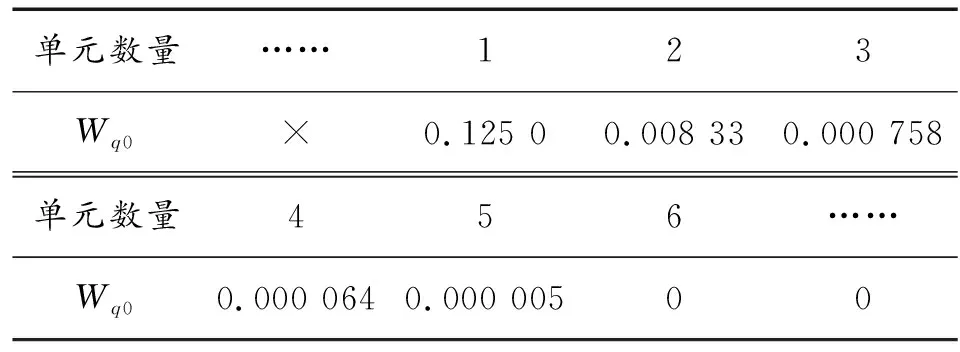
表3 通用车辆装备排队待修数量与等待维修时间

由此得到维修保障装备单元与轮式装甲装备等待维修时间之间的关系如图3所示。

由图3可知，当取2个针对轮式装甲装备的维修保障装备单元时，Wq0下降速度为最快，在此之后则趋于平缓，并且当维修保障装备单元数为2时，Wq0的值趋近于0。说明维修保障装备单元数量取2时能够在保证等待时间较短的基础之上提高排队系统工作效率的幅度是最大的，因此可将轮式装甲抢修车和保养车各配置2台。

按照上述思路可将负责对轻武器设备进行定点维修保障的轻武器设备抢修车和保养车各配置3台。

综合3.1节与3.2节的分析可得，应为该作战分队配备的维修保障装备数量如表4所示。

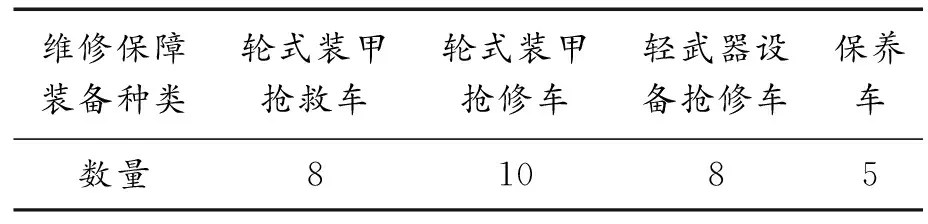
表4 作战分队维修保障装备配备数量

4 结论

本文采用排队论方法，对基于伴随维修保障与定点维修保障两种情况的维修保障装备数量确定过程进行了研究，所采用的维修保障装备数量计算方法具备一定的科学性与合理性，能够为确定部队维修力量运用规模方面的研究提供参考，具备一定的应用价值，但在多军兵种联合作战的大趋势下如何确定适用于其他军兵种力量的维修保障装备数量体系仍是有待攻克的难题，因此未来将对空军、海军的维修保障装备数量需求进行进一步研究。