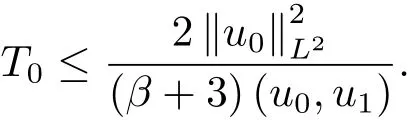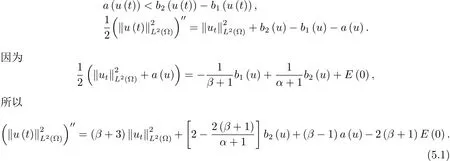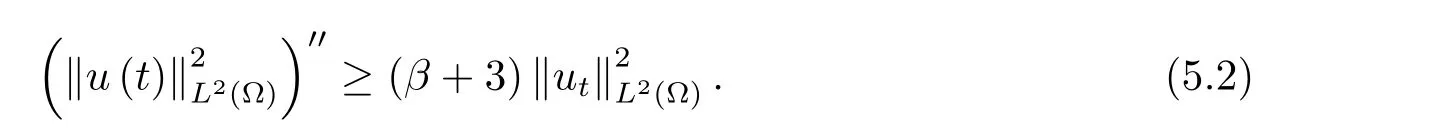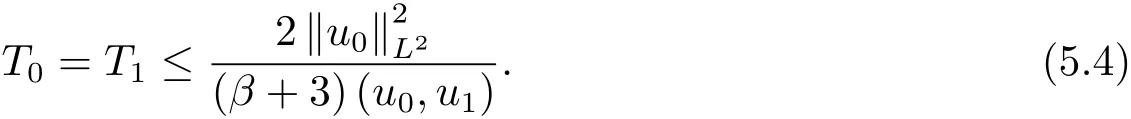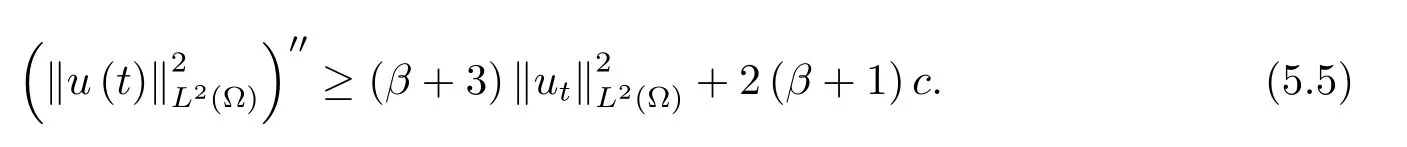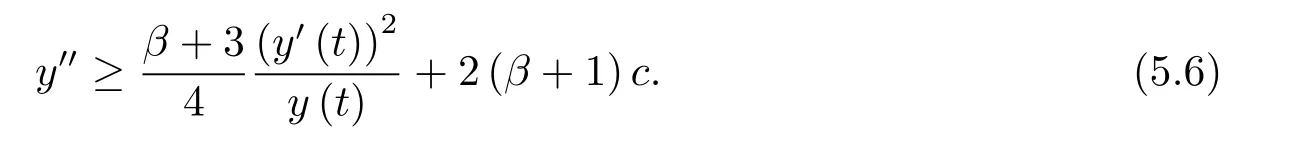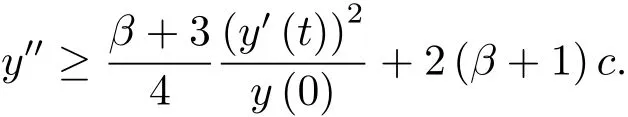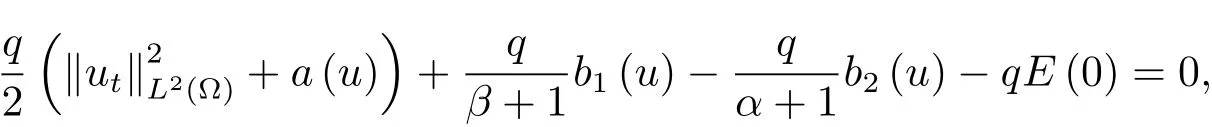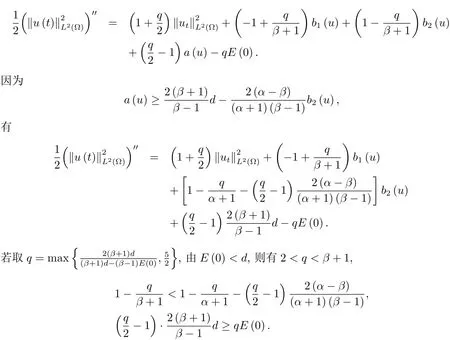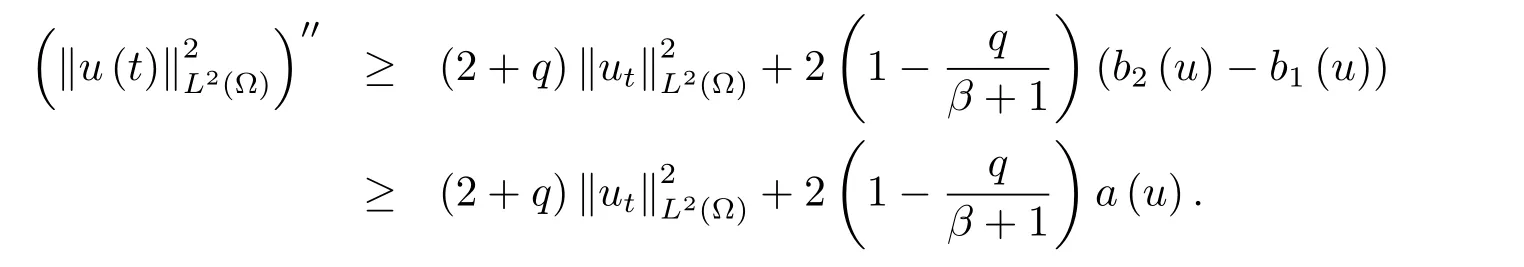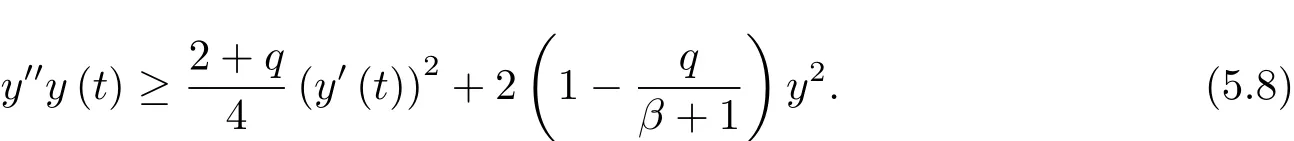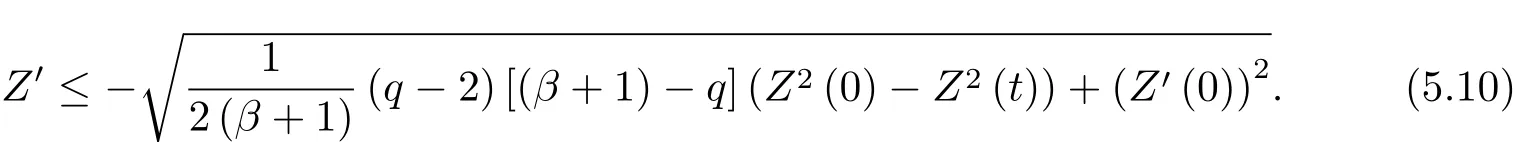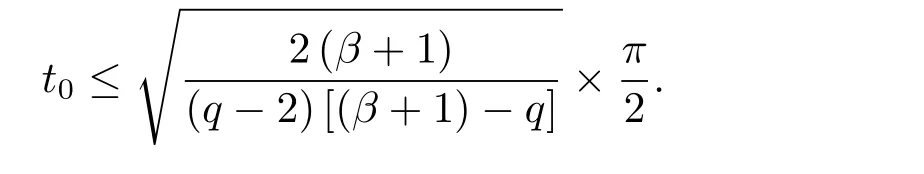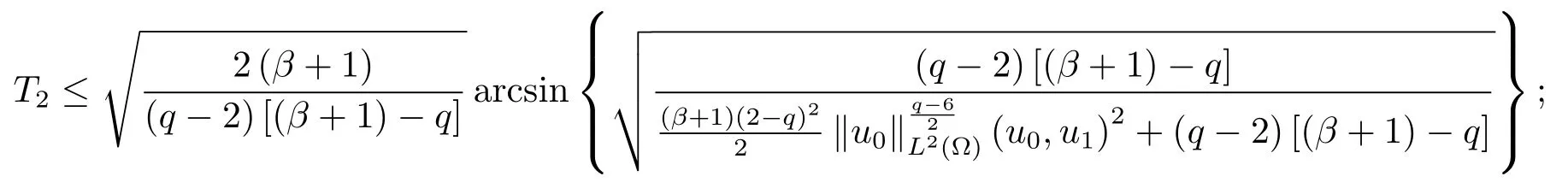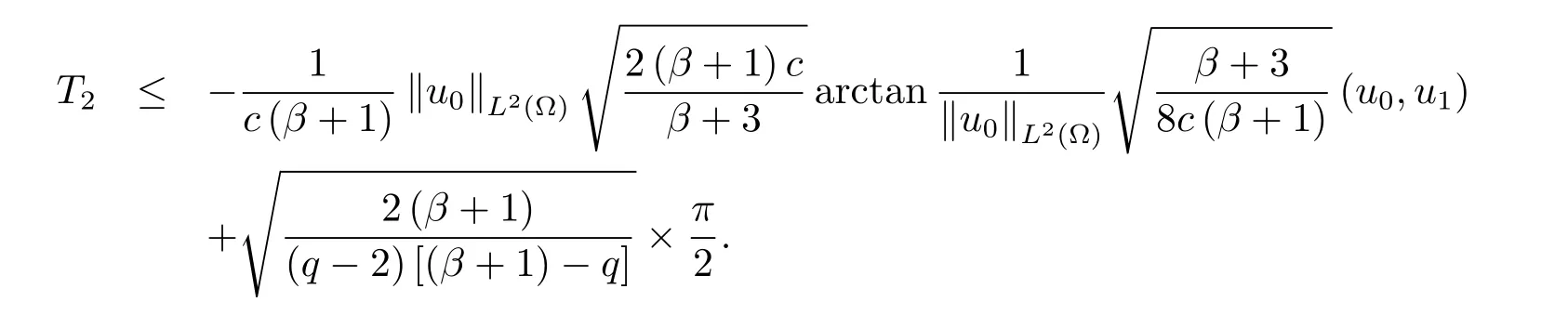一类非线性Klein-Gordon方程解的整体存在和爆破的条件
祝佳玲,李 杨,杨 晗
(西南交通大学数学学院,四川成都 611756)
1 引言
本文研究了以下非线性Klein-Gordon方程的初边值问题
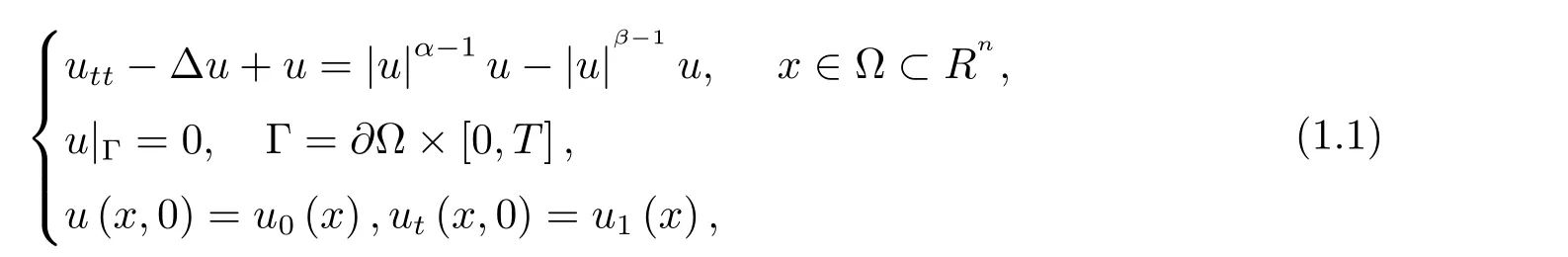
其中u=u(t,x)是复值函数,∆是Ω上的Laplace算子,Ω是Rn中带有光滑边界Γ的有界域,1≤β<α,α=β+2,且α,β是常数.当n>2时,1;当n≤ 2时,1<α<∞.
Klein-Gordon方程是相对论量子力学和量子场论中用于描述自旋为零的粒子的基本方程.对于该类方程的研究已有一些文献[1–9].值得特别指出的是:Shatah[1]证明了对非线性项f(u)(其中x∈Rn,n≥3,基态的存在性和不稳定性,得到了在不稳定基态下解不爆破的结果.黄文毅[2]对一类带有阻尼项和非负势能的非线性Klein-Gordon方程
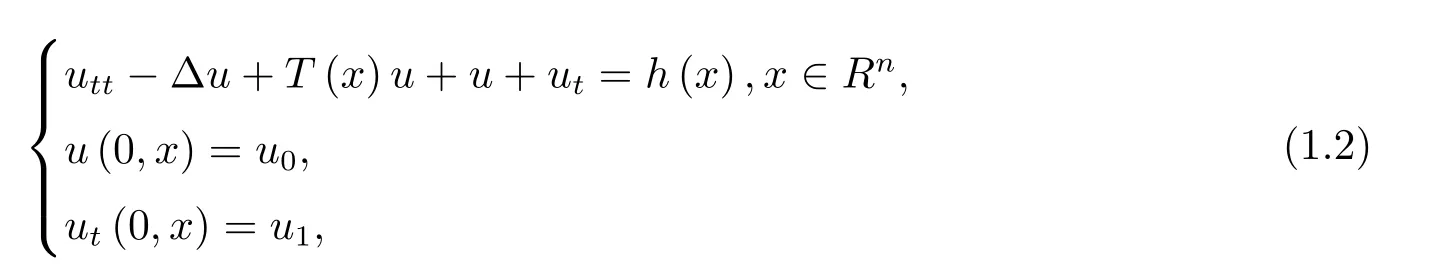
给出了当空间维数限制为n≤3时解整体存在的充分必要条件,解爆破时的生命跨度的估计等等.李考虑了不同于文献[1]的变分问题,对上不定号的情形加以了研究,Shatah的方法对此情形不适用,这也是该文的创新之处.
本文也有类似的困难,但李[9]中方程的非线性项确定了,势井深度的正性容易通过显性的方程求解来确定,而本文由于非线性项中的指数不是确定的,在确定势井深度的正性时,需要精细巧妙的讨论和估计才能确定,且文献[9]没有考虑初始能量等于势井深度临界情形下的生命跨度,这也是本文的意义所在.
2 势井深度
对u∈H1(Ω),n≤6,定义如下能量泛函

定义势井
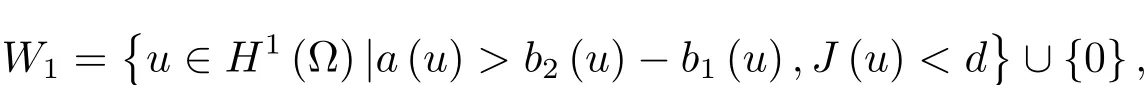
及其对应的势井外集
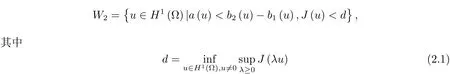
为势井深度.
下面将证明d始终大于0,即有如下引理.
引理2.1 若d由(2.1)式给出,则d>0.
证 当λ≥0时,
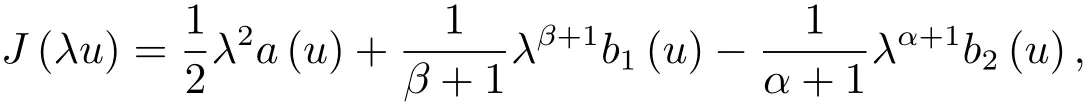
注意到 J0(λu)= λa(u)+λβb1(u)− λαb2(u)=0 存在零根.
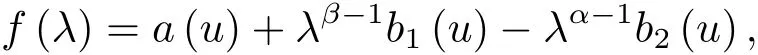
下面将证明J0(λu)=0存在正根,令注意到f(0)=a(u)>0,当λ→+∞ 时,f(λ)→−∞,因此由介值定理必然存在正根λ0,使得 f(λ0)=0,即

因为µ(Ω)<∞ (µ为Ω的Lebesgue测度),由β<α有

由于 H1(Ω) 嵌入到 Lα+1(Ω),有 kukLα+1(Ω)≤ C2kukH1(Ω),结合 (2.2) 式有
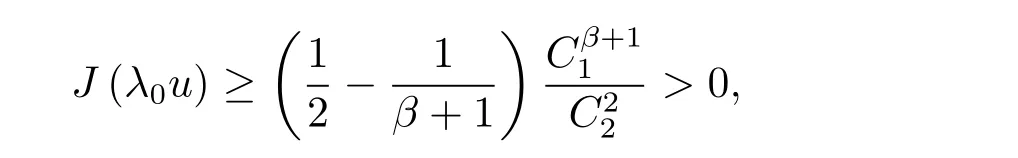
即d>0,其中c1,c2为常数.
3 解的不变集
为了得到解整体存在和爆破的条件,这一节将介绍不变集W1,W2.接下来,将利用如下事实a(u)>b2(u)−b1(u)有效等价于λ0(u)>1,a(u) 记W={u|u∈H1(Ω),J(u) 引理3.1W=W1∪W2,W1∩W2=∅. 证 W1∩W2=∅是显然的.接下来将证明W=W1∪W2.实际上,只需证明W ⊆W1∪W2.容易看到等价于 a(u)=b2(u)−b1(u)>0.因此,若λ0(u)=1,则有于是,若u∈W,u 6=0,则λ0(u)6=1等价于a(u)6=b2(u)−b1(u).这意味着u∈W1{0}或u∈W2,即W⊆W1∪W2. (不变集)若u0,u1∈Σ(其中Σ⊆H1(Ω)为集合),则(1.1)式的解u(t,x)∈Σ,把Σ叫做问题(1.1)的解的不变集. 引理3.2若 则W1和W2是问题(1.1)解的不变集. 证 由方程(1.1)有 这意味着u∈W.通常把u(x,0,u0,u1)简记为u(t). (1)令u0∈W1,可以断言u(t)∈W1.若不成立,则存在t0>0,使得u(t0)/∈W1.一方面,有u(t0)∈W2;另一方面,因为a(u(t)),b1(u(t))和b2(u(t))关于t连续,由W1和W2的定义,知存在时间t∗(0 若a(u(t∗))6=0,则λ0(u(t∗))=1.因此J(u(t∗))≥d,即u(t∗)/∈W,这与(3.2)式矛盾. 若a(u(t∗))=0,假设0 这个矛盾说明u(t)∈W1. (2)令u0∈W2,可以断言u(t)∈W2.假设不成立,即存在t0,使得u(t0)∈W1,则存在t∗,使得 a(u(t∗))=b2(u(t∗))− b1(u(t∗))(0 首先考虑a(u(t∗))=0的情况.一方面,因为a(u(t)),b1(u(t))和b2(u(t))关于t连续,可以断言 另一方面,因为对0≤ t 若a(u(t∗))6=0,则与 (1)相同的讨论有J(u(t∗))≥ d,这与(3.2)式矛盾.所以u(t)∈W2. 首先研究当初始能量E(0)=d时解整体存在和爆破的条件. 定理4.1 假设E(0)=d,u0∈H1(Ω),u1∈L2(Ω). 1)若a(u0)=b2(u0)−b1(u0),且a(u0)6=0,则问题(1.1)存在整体弱解u(t,x)∈C([0,∞);(Ω)),ut(t,x)∈ C([0,∞);L2(Ω)). 2)若a(u0)>b2(u0)−b1(u0)或a(u0)=0,则问题(1.1)存在整体弱解u(t,x)∈C([0,∞);(Ω)),ut(t,x)∈ C([0,∞);L2(Ω)). 3)若(u0,u1)≥0,a(u0) 注 当(u0,u1)<0时,添上(¯u为(1.1)式的平衡态)这个条件,同理可证,证明过程略. 证 1)若a(u0)=b2(u0)−b1(u0)且a(u0)6=0.令{wj(x)}是H1(Ω)的一个基,构造问题(1.1)的近似解um(t,x),使得 对于充分大的m,有 即 u(t,x)∈ C([0,∞);H10(Ω)),ut(t,x)∈ C([0,∞);L2(Ω)). 2)若a(u0)>b2(u0)−b1(u0)或a(u0)=0,可以断言 或 a(u)=0,对所有的t≥0成立. 实际上,如果存在t1,使得 那么由于a(u(t)),b1(u(t))和b2(u(t))关于t连续,则存在t0,使得 对t0 由于a(u(t0))6=0且a(u0)6=b2(u0)−b1(u0),所以有u(t)6≡u(t0),对0≤t≤t0成立.令 v(t)=u(t0−t)6≡ u(t0),则 v(0)=u(t0),v(t0)=u0,vt(0)=ut(t−t0)=0,v(t)满足 然而u(t0)也是以上问题的一个解,这和解的唯一性矛盾.因此(4.6)式是有效的,类似1)的证明得 u(t,x)∈ C([0,∞);H10(Ω)),ut(t,x)∈ C([0,∞);L2(Ω)). 3)与2)的证明类似,若a(u0) 若(u0,u1)≥0,则存在使得t0>0,使得(u(t0),ut(t0))实际上,若由(4.8)和(4.9)式有 对所有t≥0成立,即 是有限的.因此 由a(u),b1(u),b2(u)≥0知对所有的t≥0,a(u),b1(u),b2(u)有限.由引理3.2的证明知存在序列又由 (4.8)式知 上式矛盾.这个矛盾说明存在t1>0,使得对所有的t>0成立,因此有当然,存在t2>t1,使得因此有 对t≥t2.结果 对t>t2.因为对t>t1,对是递减的凹函数,因此存在T<+∞,使得即 其次考虑当初始能量E(0) 定理4.2 假设n≤6,0 1)若a(u0)−b2(u0)+b1(u0)>0(或a(u0)−b2(u0)+b1(u0)=0),则问题(1.1)有整体弱解 u(t,x)∈ C([0,∞);H10(Ω)),ut(t,x)∈ C([0,∞);L2(Ω)). 2)若a(u0)−b2(u0)+b1(u0)<0,则问题(1.1)的解在有限时间内爆破. 证 1)同定理4.1中1)的证明,由E(0) 所以J(u0) 且um(0)∈W1.同引理3.2,由(4.12)式对于充分大的m和0≤t<∞,可以证明um(t)∈W1且 因此 其中 c∗为常数,所以 u(t,x)∈ C([0,∞);H01(Ω)),ut(t,x)∈ C([0,∞);L2(Ω)). 2)当a(u0)−b2(u0)+b1(u0)<0时,类似定理4.1中3)的证明,易证在有限时间内爆破. 本文最后一部分将给出定理4.1和定理4.2中爆破解的生命跨度的上界估计. 定理5.1 若E(0)=d,(u0,u1)≥0,a(u0) 证 由定理4.2,对所有t≥0, 又由引理2.1的证明有 由E(0)=d,得 因为a(u0) 解上式并在0到T1上积分得 定理5.2若E(0) 1)若(u0,u1)>0,则 证 由定理4.2,对所有t≥0,同定理5.1的证明,由E(0) 因为a(u0) 将上式在0到T3上积分得 现在考虑当(u0,u1)>0时,解的生命跨度. 注意到 与(5.1)式类似可以得 由b1(u),b2(u)≥0知 因为Z0(t)<0,把(5.8)式乘以Z0,积分得 存在t0,使得Z(t0)=0,因此上式积分得 特别地,若(u0,u1)=0,即Z0(0),则 将这个结果结合(5.7)式有 1)若(u0,u1)>0,则 2)若(u0,u1)≤0,则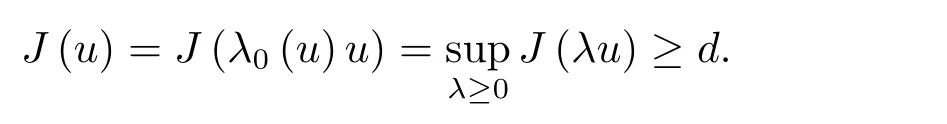
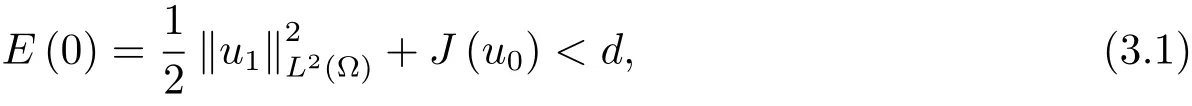
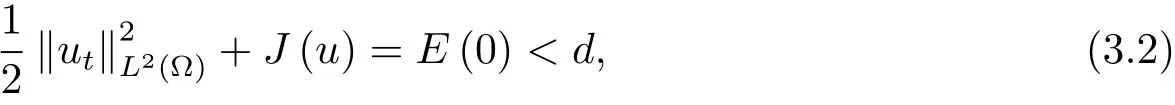
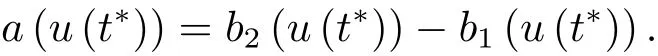
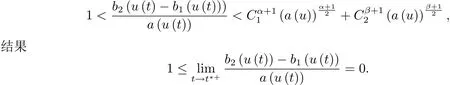
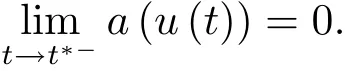
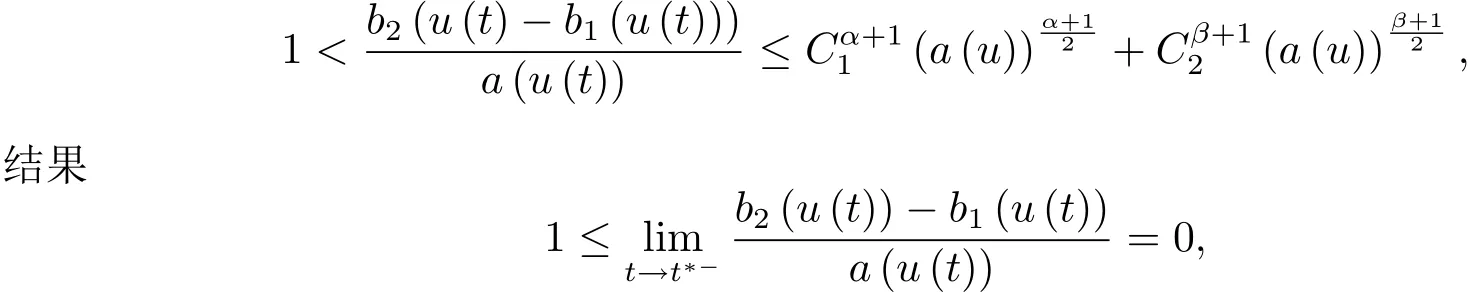
4 解的整体存在和爆破的条件

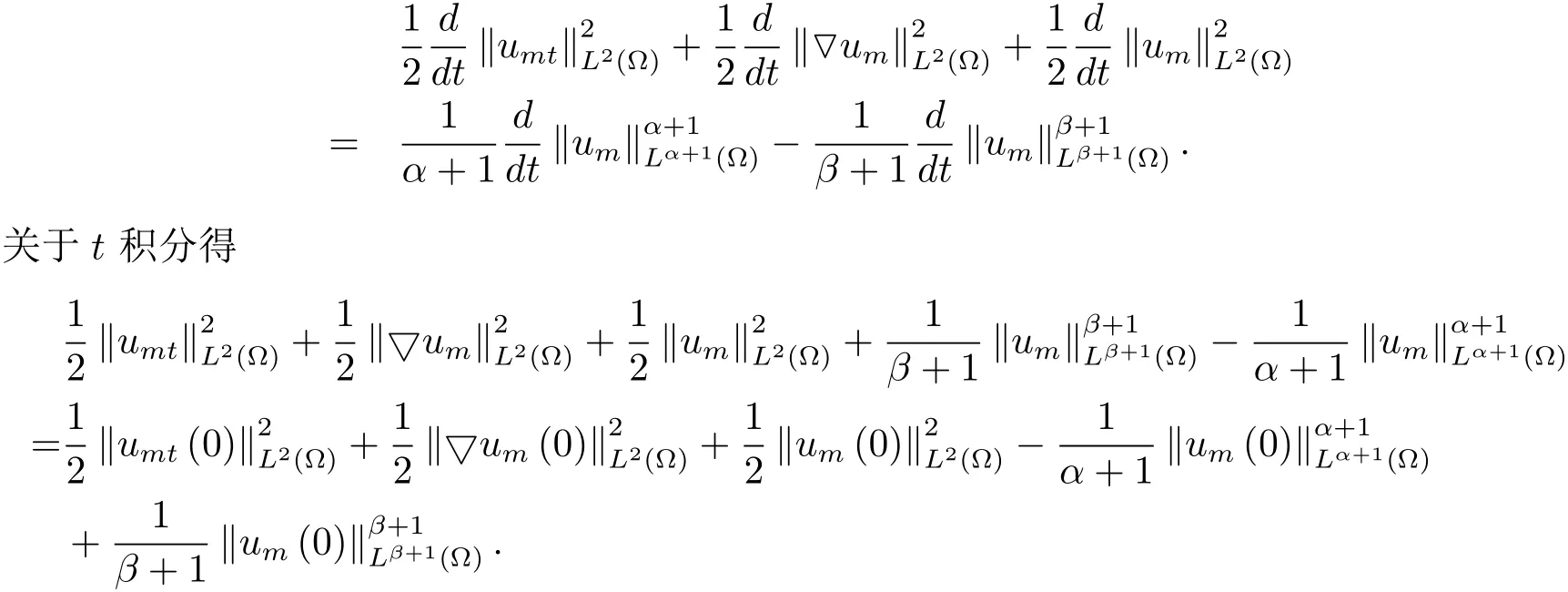
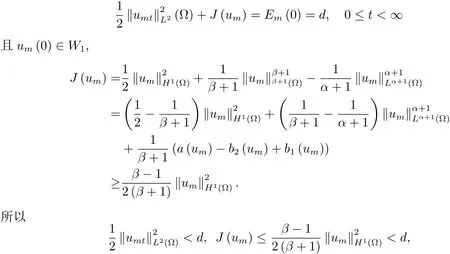
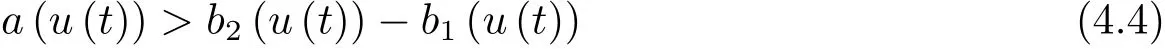
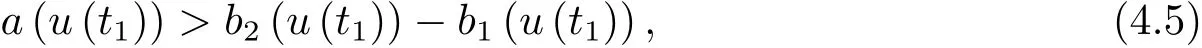
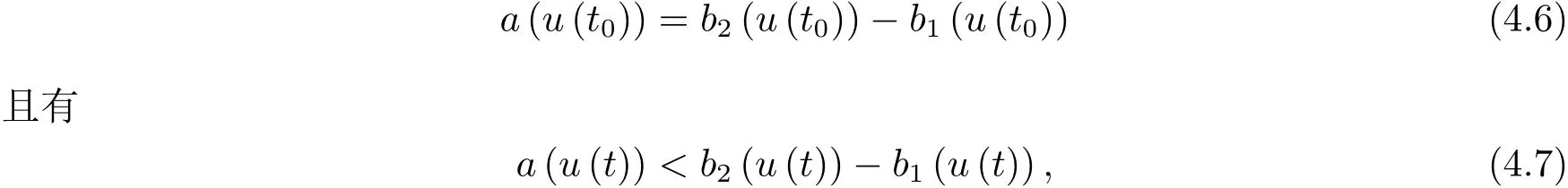
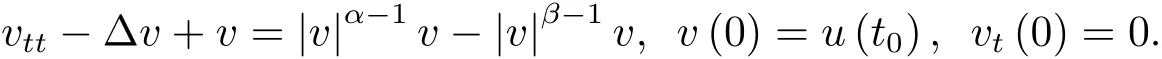
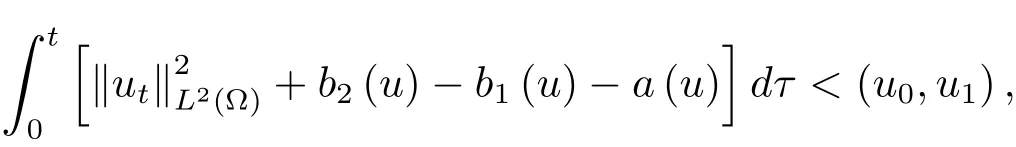

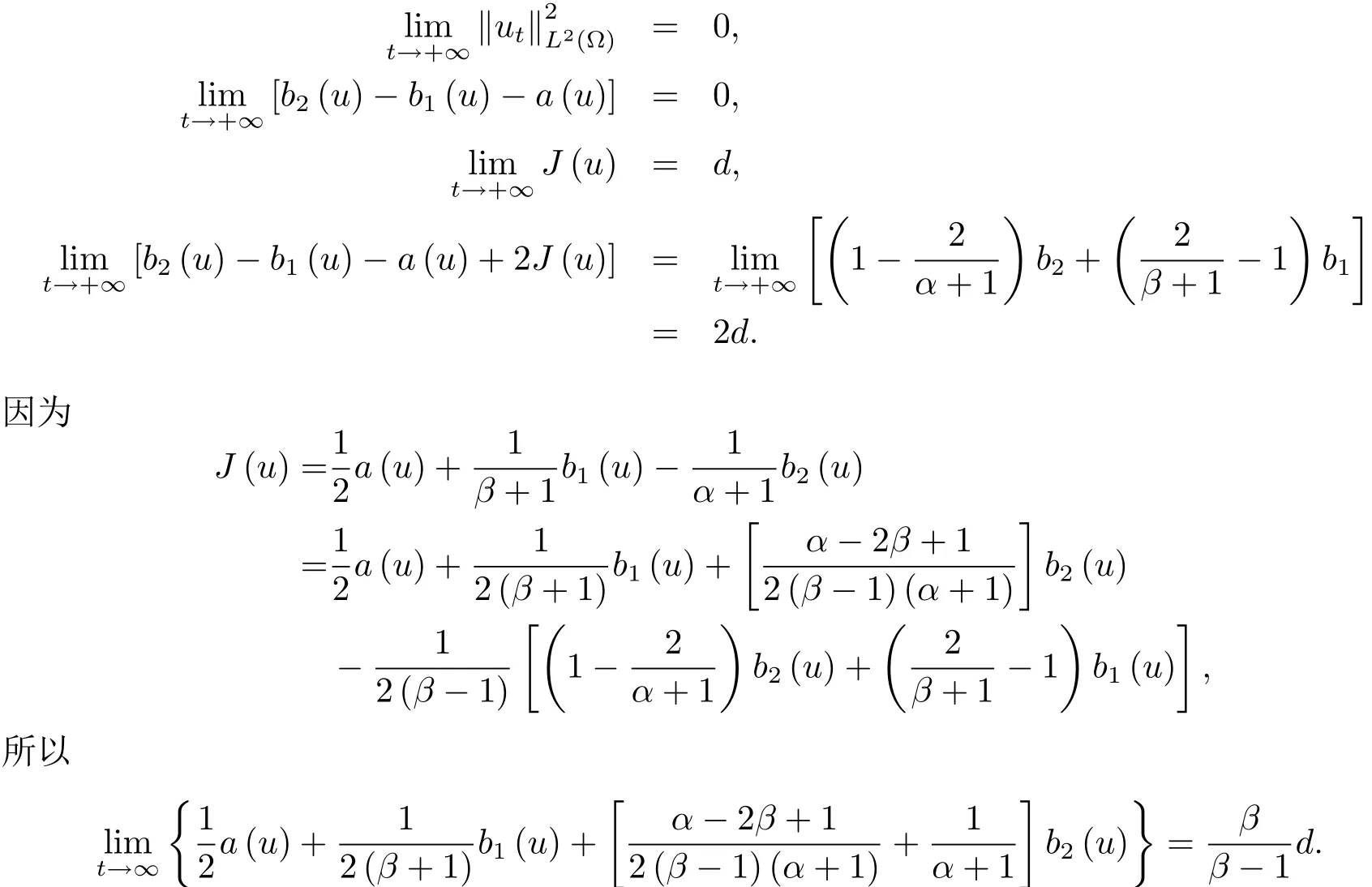
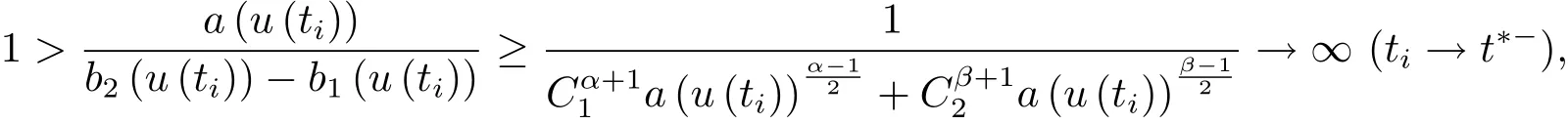
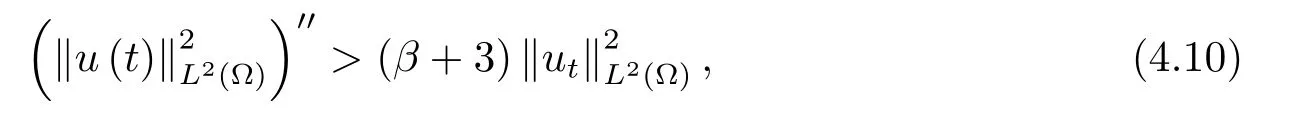
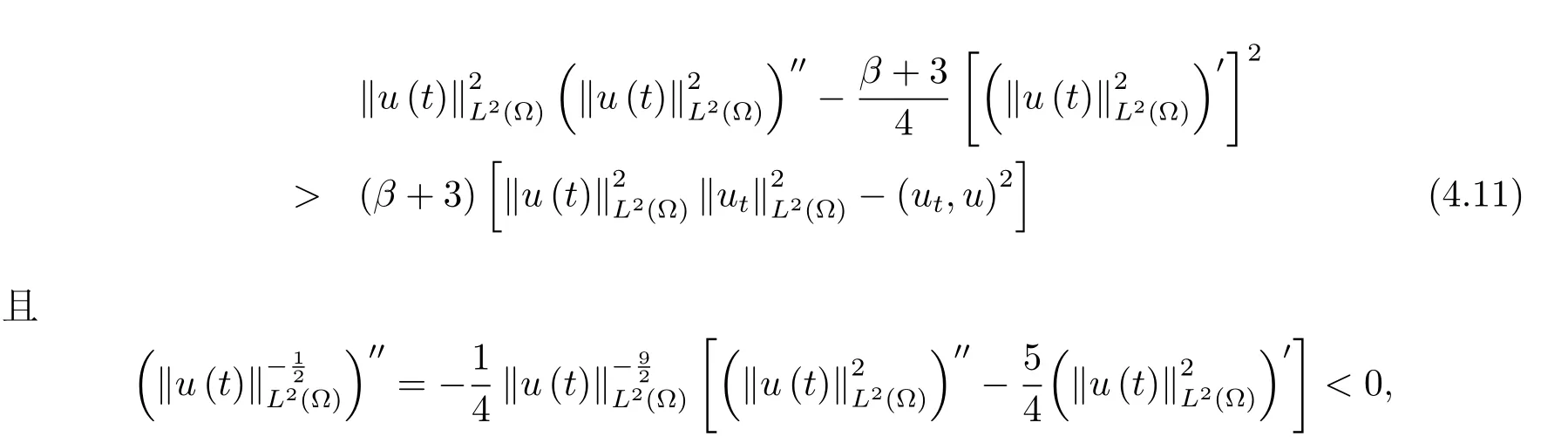
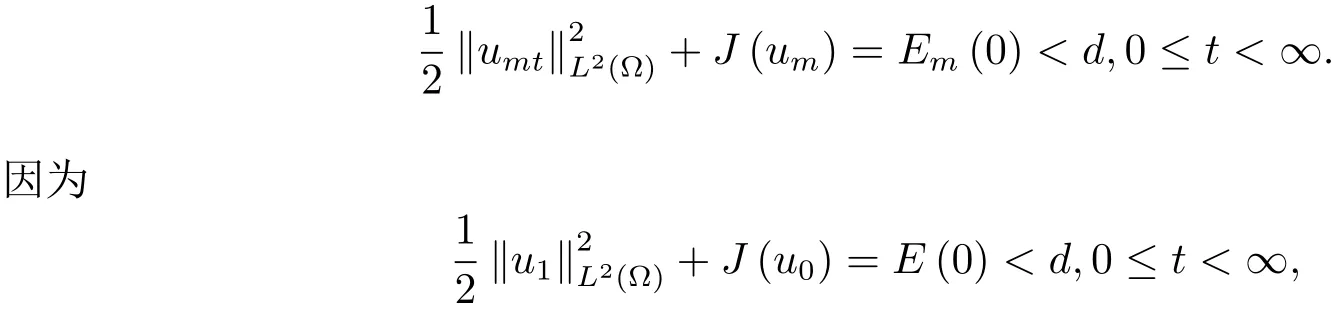
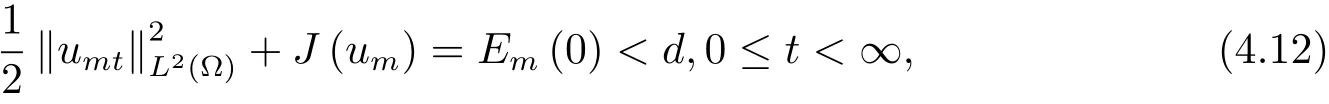

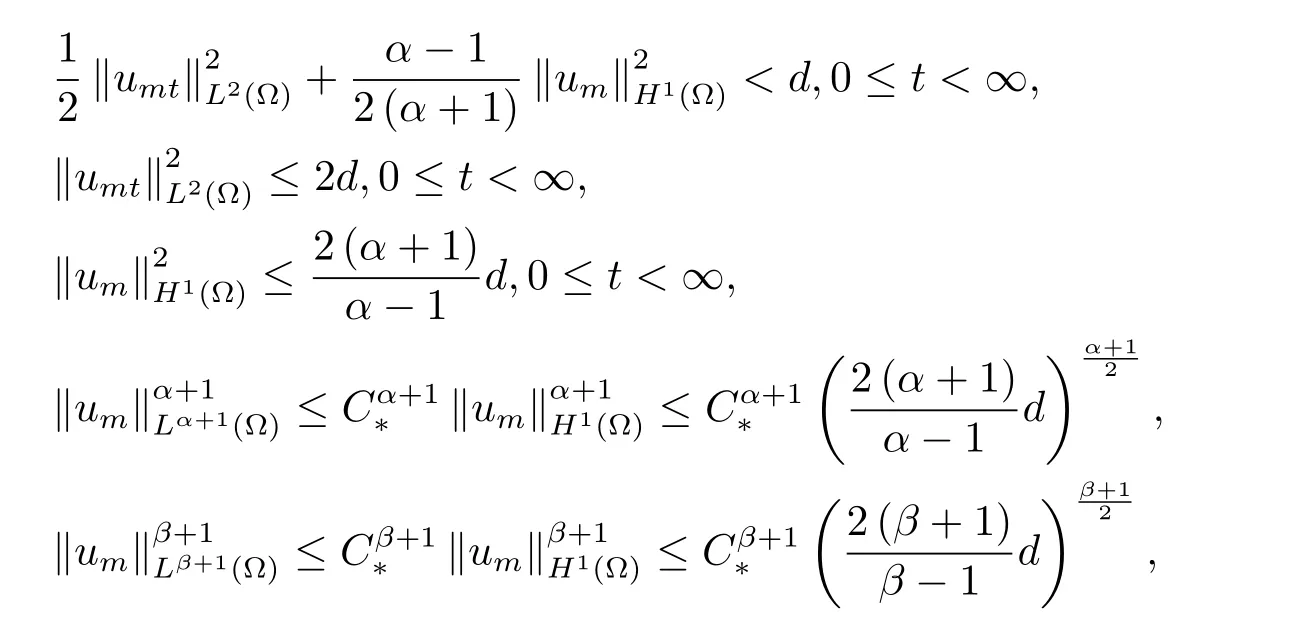
5 解爆破时生命跨度的估计