图的修正的k-顶点彩虹连通度
王万禹,王成强
(1.四川师范大学数学与软件科学学院,四川成都 610066;2.成都师范学院数学学院,四川成都 610030)


首先给出文中需要的一些定义.
定义1[8]如果路P中所有顶点着不同的颜色,或者除端点外其余内点着不同于端点的颜色且内点染色各不相同,也就是说路P中只有两个端点可以着相同的颜色,那么路P称为修正的顶点彩虹路.
定义2[8]如果图中任意两个顶点至少由一条修正的顶点彩虹路连接,则顶点着色c称为修正的顶点彩虹着色.
定义3[8]如果一个修正的顶点彩虹着色图G用了k种颜色,则称这个图G为k-可修正的顶点彩虹着色图.
定义4使得图G是修正的顶点彩虹连通图的最小颜色数目称为图G的修正顶点彩虹连通度,记做rvc*k(G).
定义5对两条u-v路P1,P2,如果V(P1)∩V(P2)={u,v},则称P1和P2为内部顶点不交的路.
定义6如果图G中任意两点间存在k条内部顶点不交的修正的顶点彩虹路,那么图G称为修正的k-顶点彩虹图.使得图G为修正的k-顶点彩虹图的最小颜色数称为修正的k-顶点彩虹连通度,记为rvc*k(G).
由定义6可知,当k=1时,rvc*1(G)=rvc*(G).只有当图G的点连通度κ(G)≥k时,图的修正的k-顶点彩虹连通度才有意义.文中研究都是在这个条件下进行的.记diam(G)为图G的直径,那么rvc*k(G)≥diam(G),当k=1,直径为1时,等式成立.
定义7令M表示一个匹配,任取一边e∈M,若e的两个端点着不同颜色,则称e为彩虹匹配边.若M中每条边都是彩虹匹配边,则称M为彩虹匹配.
定义8如果路P中所有的边着不同的颜色,那么路P称为彩虹路.
定义9如果图中任意两个顶点至少由一条彩虹路连接,则图G为彩虹连通图.使得图G是彩虹连通图的最小颜色数目k称为图G的彩虹连通度,记做rc(G).
定义10如果图G中任意两点间存在k条内部顶点不交的彩虹路,那么图G称为k-彩虹图.使得图G为k-彩虹图的最小颜色数称为k-彩虹连通度,记为rck(G).
文中主要在顶点彩虹连通度的基础上研究修正的k-顶点彩虹连通度,给出圈、轮、二部图以及完全图的修正的k-顶点彩虹连通度.以下[·]*表示上取整函数,[·]*表示下取整函数.
1 一些图类的修正的k-顶点彩虹连通度
定理1[8]对于任意正整数n≥3,有
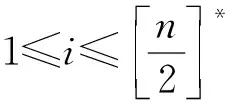
定理2当n≥3时,rvc*2(Cn)=n.
证明显然rvc*2(Cn)≤n.记Cn的着色为c,假设rvc*2(Cn)=n-1,即对于图Cn,可以用n-1种颜色对其着色,使其为修正的2-顶点彩虹连通图.在这个着色过程中,有两个顶点着色相同,记为u和v,即c(u)=c(v).
情形1.u和v相邻.
任意选择一点x∈V(Cn){u,v},对于两条x-u路,一定会有一条x-u路从x出发,经过v再到u,因c(u)=c(v),故其不是修正的顶点彩虹路.此时Cn不是修正的2-顶点彩虹连通图.
情形2.u和v不相邻.
情形2.1.若d(u,v)=2,则最短u-v路要经过一点,记为x.在另外一条u-v路中,此时x-u路中有一条路xv…ux不是修正的顶点彩虹路.
情形2.2.若d(u,v)≥3,则在最短u-v路上任取两点x,y,显然不存在两条修正的顶点彩虹x-y路,这与Cn是修正的2-顶点彩虹连通图矛盾.综合情形1-2可知,rvc*2(Cn)=n. 】
对于n≥3,轮Wn被定义为Cn+K1,K1和Cn每个顶点相连接,所以W3=K4,K1的顶点称为中心点.下面给出轮的修正的2-顶点和3-顶点彩虹连通度.
定理3对于轮Wn,有
(b)rvc*3(Wn)=n+1.


情形1.u,v∈V(Cn).
情形1.1.u,v∈V(P1)或u,v∈V(P2),不妨设u,v∈V(P1).因为P1是修正的顶点彩虹路,故顶点全在P1中的u-v路也是修正的顶点彩虹路.由着色可知,uwv是修正的顶点彩虹路.所以有2条修正的顶点彩虹u-v路.
情形1.2.u∈V(Pi)且v∈V(Pj)(i≠j,1≤i,j≤2),不妨设u∈V(P1),v∈V(P2).如果c(u)=c(v),则在Cn上有两条修正的顶点彩虹路.若c(u)≠c(v),则在Cn上距离较短的u-v路为修正的顶点彩虹路,另外一条u-v路不是.而uwv为修正的顶点彩虹路,所以在这种情形下,共有两条修正的顶点彩虹u-v路.
情形2.u∈V(Cn),v=w或v∈V(Cn),u=w.
不妨设u∈V(Cn),v=w.令vi是圈上与u相邻的一点,显然c(u)≠c(vi),所以uw(w=v)和uviw为两条修正的顶点彩虹路.
由情形1和情形2可知,着色c为Wn的修正的2-顶点彩虹着色,且
(1)

情形1.x,y,z中有一个顶点为中心点w,不妨设z=w.
在Cn中任取一点u,v-x内部不交路有3条,但是v…y…x和uwx不是修正的顶点彩虹路.故只有1条修正的顶点彩虹v-x路.这与Wn为修正的2-顶点彩虹图矛盾.
情形2.x,y,z∈V(Cn).

由情形1和情形2知
(2)
综合(1)-(2)式可知,当n≥4时,有
(b)因为Wn为3-连通图,故任意两点间有3条内部点不交的路.显然rvc*3(Wn)≤n+1成立.现在假设rvc*3(Wn)=n,那么Wn中有两个顶点着相同色,记为u,v.记Wn=Cn+K1,设中心点w=K1.
情形1.u,v∈Cn.
在Cn上选择和点u相邻的顶点x,因为3条u-x路中必定有一条要经过点v,而u…v…x路不为彩虹路,所以只有2条修正的顶点彩虹u-x路,矛盾.
情形2.u∈Cn,v=w.
任选Cn上不同于u的一点x,因为三条u-x路中必定有一条要经过点v(v=w),而u…v(v=w)…x路不为彩虹路,所以只有2条修正的顶点彩虹u-x路,矛盾.
由情形1和情形2知,rvc*3(Wn)≥n+1.所以rvc3(Wn)=n+1. 】
命题1图G为完全二部图,令M表示含k条边的彩虹匹配,对于任意两点u,v∉V(M),如果uv的着色和M中顶点颜色不同,则至少存在k条顶点不交的修正的顶点彩虹u-v路.
证明因为图G为完全二部图,设G=V1,V2,E,M={x1y1,x2y2,…,xkyk},其中xi∈V1,yi∈V2(1≤i≤k).如果u∈V1,v∈V2,则路u-xi-yi-v(1≤i≤k)为修正的顶点彩虹路,共k条.另一方面,不妨设u,v∈V1,此时路u-yi-v为修正的顶点彩虹路,共k条. 】
命题2令M为含k-1条边的完美匹配,若M中有k个顶点着相同颜色,则至少存在一条边e∈M,使得e的两个端点着相同颜色.
证明因为M为含k-1条边的完美匹配,令M={x1y1,x2y2,…,xk-1yk-1}.设X={x1,x2,…,xk-1},Y={y1,y2,…,yk-1}.如果X中的顶点有s(1≤s≤k-1)个顶点着色相同,不妨设为前s个顶点(x1,x2,…,xs).当s=1或者k-1时,结论显然成立.现在假设2≤s≤k-2,因为M中有k个顶点着相同颜色,所以在Y中有k-s个顶点着色和X中前s个顶点着色相同.如果y1,y2,…,ys着色和X中前s个顶点着色不同,则在Y中剩余的k-1-s个顶点中需要有k-s个顶点和X中前s个顶点着色相同,矛盾. 】
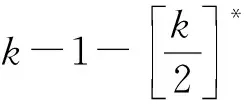

定理4令G=Kp,q(p≤q)为k连通图,则k≤p,且有
(a)rvc*(Kp,q)=2;
(b)rvc*k(Kp,q)=k+2,p≥2k-2;
(c)rvc*2(Kp,q)=4.
证明(a)令X表示含图G第一部分p个顶点的顶点集,Y表示含图G第二部分q个顶点的顶点集,即X={v1,v2,…,vp},Y={u1,u2,…,uq}.
给X中所有顶点着色1,Y中所有顶点着色2,任意两点间存在一条修正的顶点彩虹路,故rvc*(Kp,q)≤2.给G中所有顶点着色1,对任意x∈V(X),y∈V(Y),u和v之间不存在修正的顶点彩虹路,故rvc*(Kp,q)≥2.所以rvc*(Kp,q)=2.
(b)将顶点集X拆分成k个子集,记为{X1,X2,…,Xk},满足条件X=X1∪X2∪…∪Xk,X2=X3=…=Xk,X1=p-k+1.因为G为完全二部图,所以存在G的一个完备匹配M满足条件M=M1∪M2∪…∪Mk且V(Mi)∩V(Mj)=∅(i≠j),其中Mi为顶点子集Xi(1≤i≤k)到Y中某一顶点子集Yi之间的完备匹配且Mi=Xi.
当p=q时M为完美匹配.接下来给出G的一个着色法c:X1中所有点着色1,Xi(2≤i≤k)着色2.Yi的着色记为c(Yi)=i+2(1≤i≤k).若p 下面证明着色c为图G的修正的k-顶点彩虹着色.先讨论p=q的情形,此时图G为正则的完全二部图.任取两点u和v. 情形1.u,v分别在X1和Y1上. 不妨设u∈X1,v∈Y1.此时除含X1的顶点的匹配外,还有k-1条彩虹匹配.由命题1知,除uv路外,还有k-1条内部顶点不交的修正的顶点彩虹路. 情形2.u∉X1或者v∉Y1. 情形2.1.当u∉X1且v∉Y1时,如果u,v来自于XX1或YY1,此时有p条内部顶点不交的修正的彩虹u-v路.如果有一点,不妨令为u使得u∈XX1,则另一点v∈YY1,此时有p-k+2条修正的彩虹u-v路,因为p≥2k-2,所以p-k+2≥k. 当q≥p+2时,结合上述p=q讨论,任取两点u,v,我们只需讨论以下3种情况. 由上述讨论知,c是图G的修正的k-顶点彩虹着色,所以当p≥2k-2时,rvc*k(Kp,q)≤k+2. 先讨论p=q的情形.因为rvc*k(Kp,q)=k+1,故2k(p=q)或2k+1(p 情形1.若X的k部分顶点着相同颜色(此情形和Y中k部分顶点着相同颜色情形相同).此时c(Yi)≠c(Yj)(i≠j,1≤i≤k))且和X中顶点着色不同.取u∈X,v∈Yi,则有且仅有一条u-v修正的顶点彩虹路,即uv,矛盾. 情形2.X中有s个以及Y中有t个顶点子集着相同色,满足s+t=k,s,t≠0. 情形2.1.c(X1)=c(Y1).取u∈X,v∈Y2.因为c(X1)=c(Y1),故经过M1中的边的u-v路不是修正的顶点彩虹路,故至多有k-1条内部不交的修正的顶点彩虹u-v路. 情形2.2.c(X1)≠c(Y1). ( i )假设X中s个顶点子集(含X1),不妨设s个部分为X1,X2,…,Xs和Y中t=k-s个顶点子集(不含Y1),不妨记为Yi1,Yi2,…,Yik-s着相同颜色1,X和Y中剩余的共k个子集着不同于1的颜色且每个部分着一个新的颜色,颜色集为{2,3,…,k+1}.取u∈Y1,v∈X2,由划分X=X1∪X2∪…∪Xk,X2=X3=…=Xk,X1=p-k+1可知,此时内部顶点不交的修正的顶点彩虹u-v路有p-(p-k+1)-(s-1)=k-s(≤k-1)条,矛盾. ( ii ){X2,X3,…Xk}中有s个顶点子集和Y中k-s个顶点子集(含Y1)着相同颜色.记s个子集为{Xi1,Xi2,…,Xis},Y的含Y1的k-s个子集,不妨记为{Y1,Y2,…,Yk-s}.取u∈X1,v∈Y2,同情形2.2,有k-s(≤k-1)条内部顶点不交的修正的顶点彩虹u-v路,矛盾. 由上述证明可知,当p=q时,rvc*k(Kp,q)=k+2(p≥2k-2). 由p=q的讨论可知,当图G的着色数为k+2时,若u∈Yj,则对于任意点v,至少有k条内部不交的修正的顶点彩虹路.因此,只需要再讨论以下两种情况即可. (1)v∈Yk+1,u∈Yj.在p=q的情况下,按照对图G的着色,当u∈Yj时,对于任意点w,都至少有k条内部不交的修正的顶点彩虹w-v路.现在c(u)=c(v),故对于任意w≠u,至少有k条v-w内部不交的修正的顶点彩虹路.当w=v时,有p(≥k)条内部不交的修正的顶点彩虹路. (2)v∈Yk+1,u∈Yk+1,此时q≥p+2.由着色c可知,有p(≥k)条内部不交的修正的顶点彩虹u-v路. 故对于p 由(b)知,当k=2时,(c)显然成立. 】 定理5对于完全图Kn,有 (a)rvc*(Kn)=1; (b)rvc*k(Kn)=k+1,2≤k≤n-1. 证明(a)显然成立. (b)设Kn的顶点集为V={v1,v2,…,vn},则Kn包含一个Hamilton圈,记为Cn,且Cn为Kn的一个生成子图.令Cn=v1v2…vnvn+1(vn+1=v1).从n个顶点中任选k个,记含这k个顶点的集合为X={vi1,vi2,…,vik},剩余顶点组成的集合记为Y=VX.现在给出Cn的一个点着色c.对于X中每一个不同的顶点着不同的颜色,共需要k种颜色,记这k种颜色为{1,2,…,k}.对于Y中顶点,每一个顶点着颜色k+1.对Cn的着色一共用了k+1种颜色.接下来证明c是修正的k-顶点彩虹着色.任取图中两点u,v. 情形1.u,v∈X.因为Kn为完全图,所以有n-1(≥k)条内部不交的修正的顶点彩虹u-v路. 情形2.u∈X,v∈Y.对于任意y∈Xu,uyv是修正的顶点彩虹路,这样的路有k-1条,而uv也是修正的顶点彩虹u-v路,所以共有k条. 情形3.u,v∈Y.对所有的x∈X,uxv都为修正的顶点彩虹路,共有k条,而uv也是彩虹顶点路,所以共有k+1条修正的顶点彩虹u-v路. 所以c为修正的k-顶点彩虹着色,因而当2≤k≤n-1时,rvc*k(Kn)≤k+1. 假设rvc*k(Kn)=k,即用k种颜色可以使Kn为修正的k-顶点彩虹图,那么Cn中有k-1个顶点着不同颜色,剩余的n-k+1个顶点全部着一个相同的新的颜色.记着不同颜色的k-1个顶点的集合为X,剩余顶点的集合为Y.取u∈X,v∈Y.除uv路外,对于任意点x,要使uxv为修正的顶点彩虹路只有x∈X{u},这样的x有k-2个,加上uv,内部不交的修正的顶点彩虹u-v路只有k-1条,矛盾. 综上所述,当2≤k≤n-1时rvc*k(Kn)=k+1. 】 下面给出了圈、轮、二部图以及完全图的修正的k-顶点彩虹连通度.一个有趣的问题就是哪些图的rc(G)大于rvc*(G),哪些图的rvc(G)大于rc(G),在什么情况下二者又相等.由定理4(a)可知,rvc*(K1,q)=2,而rc(K1,q)=q,当q≥2时,rc(K1,q)≥rvc*(K1,q).现在来构造一个图G:首先给出t个顶点不交的三角,接着在每个三角中选择一个顶点,共t个,然后将这t个顶点连接起来构造成一个t阶完全图,能够得到rvc*(G)=rc(G)=t+1.在这部分中,目的是比较rck(G)和rvc*k(G),希望找到一些图使得图的k-彩虹连通度大于其修正的k-顶点彩虹连通度. 首先构造一个rck(G)大于rvc*k(G)的图G.图G是由一条路和一个星图所构成,具体的构造方式如下:令P=v0v1…vt是长为t的路,然后作一个以vt为中心点含s片叶子(记为u1,u2,…,us)的星图,这样的图记为Lt,s,如图1所示. 图Lt,s中顶点vi着色i+1(0≤i≤t),uj(1≤j≤s)着色1.容易证明rvc*(Lt,s)=t+1.对于Lt,s中的边vivi+1(0≤i≤t-1)着色i+1,对于Lt,s中属于星图部分的边(共s条),每一条边着一个新的颜色,这个过程一共用了t+s种颜色,容易证明rc(Lt,s)=t+s.于是,给定两个正整数a,b,当1≤b≤a时,存在一个图H满足rc(G)=a,rvc*(H)=b+1,此时H=Lb,a-b.由此可得下面结果. 定理6若两个正整数t,s满足1≤t 证明通过图Lt,s按以下步骤来构造满足定理6的图(如图2): 图1 图Lt,s图2 满足定理6的图G Fig 1GraphLt,sFig 2GraphGsatisfying theorem 6 ( i )将图Lt,s中的顶点v1,v2,…,vt分别用含k个顶点的团Kk替代,这k个团的顶点集依次记为X1,X2,…,Xt; ( ii )v0和X1中每个顶点用边相连,对于所有的1≤i≤t-1,Xi和Xi+1中所有顶点之间用边相连(如果t≥2)),对于所有的1≤j≤s,uj和Xt中每一个顶点用边相连.
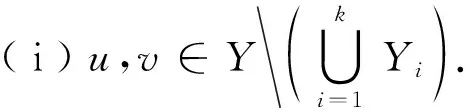



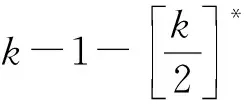

2 rck(G)和rvc*k(G)的比较



