大型LNG储罐外罐长期预应力损失分析

程旭东 王子栋 马 川 王洪杰 张如林

中国石油大学（华东）储运与建筑工程学院

0 引言

国内大型LNG全容罐外罐多采用预应力钢筋混凝土结构建造。外罐在混凝土浇筑期间，由于水化热作用极易产生温度裂缝；在内罐液化天然气泄露的异常工况下，外罐由于液压和气压作用以及内外侧的温差作用将处于受拉状态而产生裂缝[1-3]。因此在设计外罐时对其施加环向及竖向预应力，使外罐混凝土长期处于受压状态来控制裂缝的开展。在设计时必须考虑预应力的损失，特别是长期预应力损失。若长期预应力损失考虑过小，将严重影响储罐正常使用及安全性能；但考虑过大，增加初始张拉控制应力，不仅增大成本，还将引起外罐罐壁底部和顶部因约束作用而产生新的裂缝[4]。

国内外的相关规范对长期预应力损失计算进行了规定[5-9]，也有国内外学者针对LNG储罐及类似结构的长期预应力损失计算进行了一定的研究[4,10-14]，但现有的理论计算中大多针对只施加单向预应力的构件，且鲜有考虑混凝土收缩徐变及预应力筋应力松弛的相互作用对长期预应力损失的影响。为此，根据长期预应力损失计算理论，应用大型通用有限元软件ABAQUS，分析了收缩徐变、应力松弛及其相互作用对长期预应力损失的影响，以及环向和竖向预应力对彼此长期预应力损失的交互影响。

1 长期预应力损失计算理论分析

1.1 混凝土徐变的线性叠加理论

混凝土徐变机理十分复杂，针对混凝土徐变的计算，通常认为混凝土徐变与应力之间存在着线性关系并遵循Bolzman叠加原理[15]。近海环境下的大型LNG储罐其力学状态[16]及环境状态符合叠加原理的适用范围[15]。混凝土由收缩徐变产生的应变为每一段应力增量造成的应变总和。当应力连续变化时，其表达式[17]为：

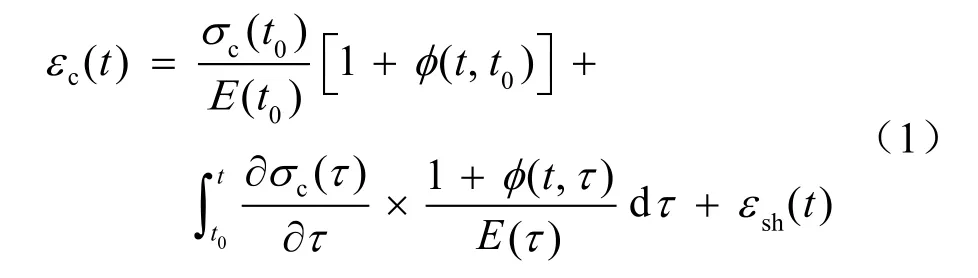
式中εc(t)表示混凝土应变；t表示计算时刻的混凝土龄期，d；σc(t0)表示t0时混凝土应力，MPa；t0表示预加应力时的混凝土龄期，d；E(t0)表示t0时混凝土弹性模量，MPa； (t, t0)表示混凝土加载龄期为t0时，t时刻混凝土徐变系数；τ表示积分项中的混凝土加载龄期，d；σc(τ)表示混凝土加载龄期为τ时混凝土应力，MPa； (t, τ)表示混凝土加载龄期为τ时，t时刻混凝土徐变系数；E(τ)表示加载龄期为τ时混凝土的弹性模量，MPa；εsh(t)表示混凝土收缩应变。

1.2 长期预应力损失计算公式

通常认为预应力筋与混凝土变形协调，且任意截面预应力筋应力减小值与混凝土及普通钢筋压应力增大值相等，其表达式分别为：

式中εc(t0)表示t0时混凝土应变；εp(t)表示预应力筋应变；εp(t0)表示t0时预应力筋应变；σc(t)表示混凝土应力变化值，MPa；Ap表示预应力筋截面面积，mm2；Ac表示混凝土换算截面面积，mm2；σp(t)表示预应力筋应力变化值，MPa。

理论计算中不考虑预应力筋应力松弛与混凝土收缩徐变的相互作用，当预应力筋产生应力松弛时，预应力筋的应力应变关系为：

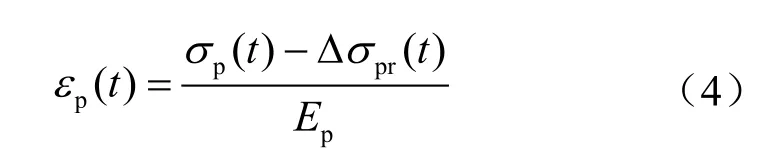
式中 表示预应力筋的应力松弛损失，MPa；Ep表示预应力筋的弹性模量，MPa。

由公式（1）～（4）整理可得分项叠加的考虑收缩徐变和预应力筋应力松弛的长期预应力损失方程：

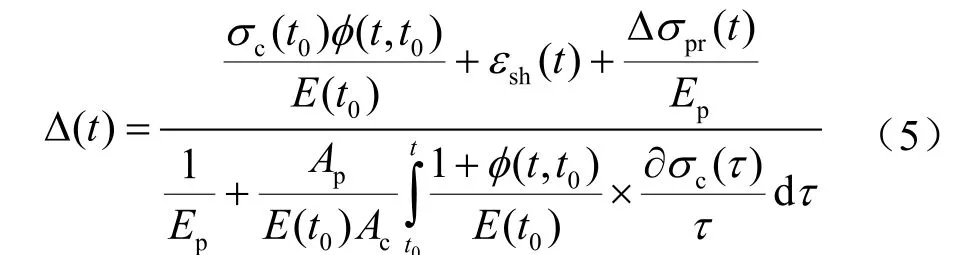
针对线性徐变理论中的积分中值解，Bazant提出按龄期调整的有效模量法[18]将其转变为代数方程解，提出等效的老化系数，将积分项简化：

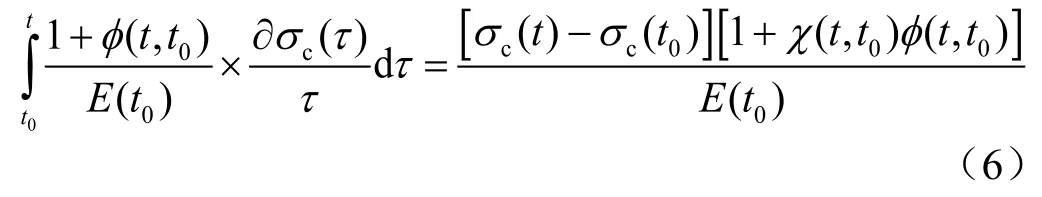
式中χ(t, t0)表示老化系数，其取值范围为0.5＜χ(t, t0)＜1。

然而实际情况下，预应力筋的应力松弛随着时间的发展将会导致混凝土预应力的降低，而混凝土徐变与其受荷载时期的荷载大小关系显著。收缩徐变对构件尺寸产生长期影响，使构件缩短，从而降低预应力筋预应力，此应力降低值又会对预应力筋应力松弛产生影响。因此收缩徐变和应力松弛二者存在相互作用关系，不考虑二者相互作用关系将导致长期预应力损失计算结果偏大。此外，理论计算未考虑双向预应力对预应力损失计算所带来的影响，老化系数使用时需要查表差且仍存在一定误差给实际工程中的应用带来不便[17]。因此有必要将按龄期调整的有效模量法与有限单元法相结合，以提高长期预应力损失的计算精度[19]。

1.3 不同规范中针对长期预应力损失的计算方法

针对长期预应力损失的计算，我国混凝土结构设计规范[5]中提供了相应分项计算公式而后叠加的方法；欧洲规范[8]中考虑相互作用影响，将应力松弛项乘以系数0.8来近似考虑相互作用；美国规范[9]中提出近似计算法和精确计算法，精确计算法考虑了分批张拉对损失造成的影响，但此方法也未考虑相互作用对长期预应力损失造成的影响。因此针对LNG储罐外罐，有必要建立相应的有限元模型来模拟收缩徐变及应力松弛的相互作用对长期预应力损失造成的影响。

1.4 长期预应力损失在ABAQUS中的实现方法

1.4.1 混凝土徐变的实现方法

采用铁道部相关设计规范TB 10002.3—2005[6]，参考欧洲规范的徐变模型，根据LNG储罐外罐实际工况进行参数取值，计算得出徐变系数随时间的变化曲线。通过增量步的设置对按龄期调整的有效模量法进行精确计算，相关计算公式如下：

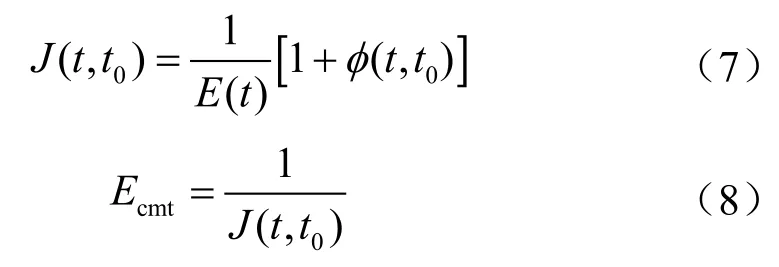
式中J(t, t0)表示t0时刻加载的混凝土弹性柔度，1/MPa；Ecmt表示输入到ABAQUS的混凝土有效弹性模量，MPa。

将时变有效弹性模量以表单的形式输入到ABAQUS的材料属性中，构造一个虚拟场变量，并修改ABAQUS中的关键词，通过场变量建立弹性模量与时间增量步之间的联系。

1.4.2 混凝土收缩的实现方法

采用铁道部相关设计规范TB 10002.3—2005[6]，参考欧洲规范的收缩模型，根据LNG储罐外罐实际工况进行参数取值，计算出混凝土收缩应变随时间的变化曲线。将混凝土收缩应变等效为混凝土温度变化，并通过设定幅值函数的形式添加到混凝土的预定义温度场中。混凝土收缩应变的等效公式如下：

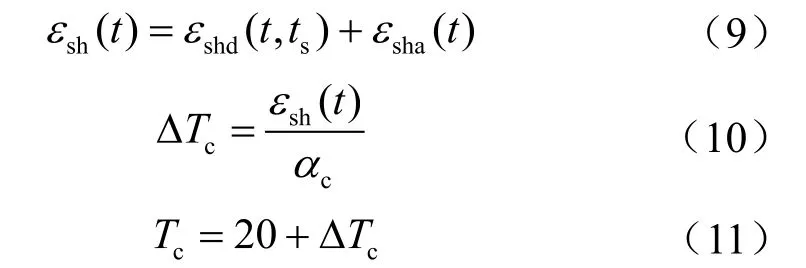
式中εshd(t,ts)表示干燥收缩应变；εsha(t)表示自收缩应变；ts表示混凝土干缩开始时间，这里取3 d；ΔTc表示混凝土温度变化，℃；αc表示混凝土膨胀系数，1/℃；Tc表示需要在ABAQUS中输入的混凝土温度，℃。

1.4.3 应力松弛的实现方法

应力松弛的实现方法与混凝土收缩类似，将预应力筋松弛率转化为预应力筋的温度变化，设定相应的幅值函数，添加到预应力筋的预定义温度场中。预应力筋应力松弛损失的等效公式如下：

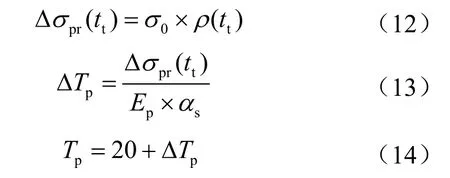
式中tt表示张拉后的时间，d；σ0表示初始预应力，MPa；ρ(tt)表示时变预应力筋松弛率；αs表示预应力筋膨胀系数，1/℃；ΔTp表示预应力筋温度变化，℃；Tp表示需要在ABAQUS中输入的预应力筋温度，℃。

由于混凝土结构设计规范中应力松弛损失仅给出40 d的损失终值公式，本文采用欧洲规范中的时变松弛率[18]。将预应力钢绞线按松弛率的高低分为普通松弛预应力钢绞线和低松弛预应力钢绞线，其松弛率公式分别为：

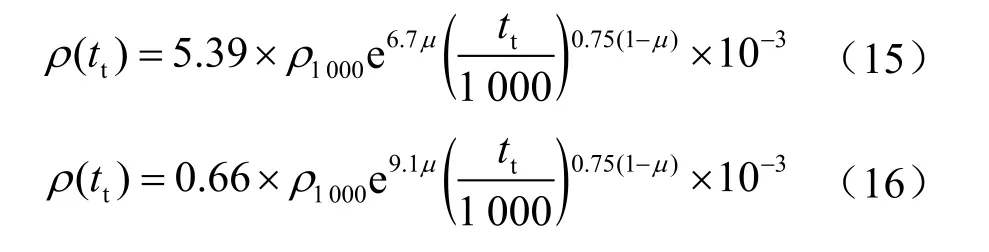
式中μ表示初始预应力与预应力筋抗拉强度比值，本文取0.7；ρ1000表示平均温度为20 ℃的条件下张拉1000 h后的松弛率。

2 ABAQUS有限元模型

2.1 大型LNG储罐实际结构

大型LNG预应力混凝土储罐一般由内罐和外罐组成，内罐采用9%镍钢，外罐为预应力混凝土结构，中间采用膨胀珍珠岩作为隔热层。其中外罐由圆柱形罐壁、罐底及球形穹顶三部分组成。国内某大型预应力LNG储罐混凝土外罐壁内侧半径（R）41 m，罐壁厚（t）0.8 m，高度（H）40 m，如图1所示。外罐罐壁混凝土采用C50建造，罐壁壁厚中间位置布置12T15水平的环向预应力筋（以下缩写为C-T）99束及8T15竖向预应力筋（以下缩写为V-T）140束，罐壁外侧及内侧分别布置普通钢筋及低温钢筋网，保护层厚度为50 mm。详细的相关计算参数如表1所示。

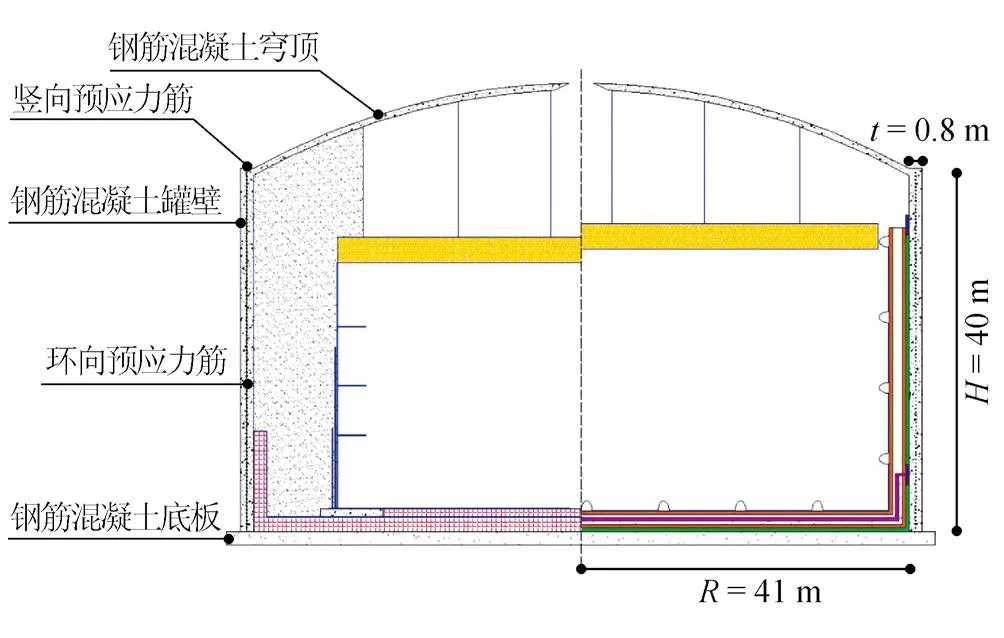
图1 LNG储罐外罐结构剖面示意图

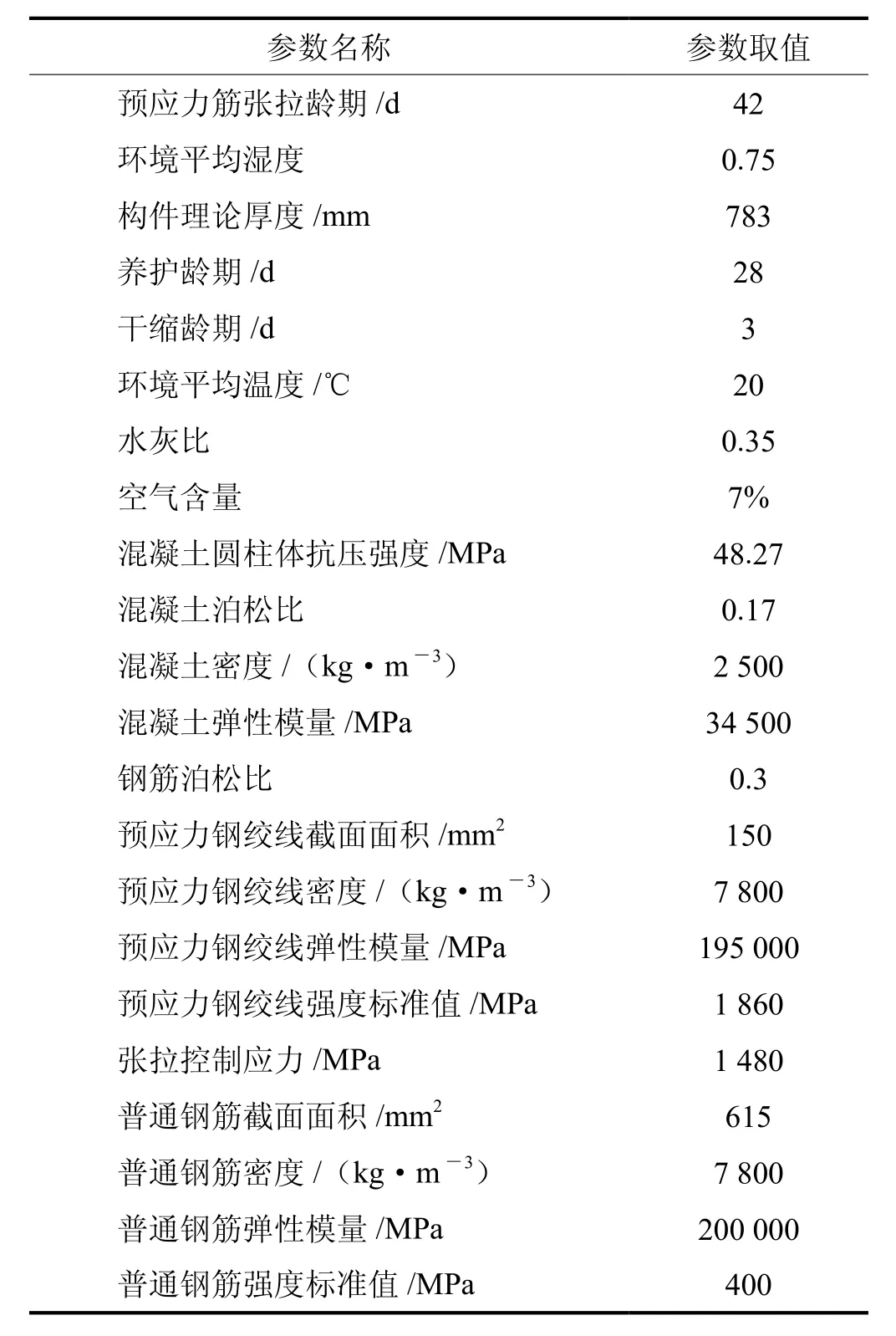
表1 计算相关工程参数表

依据混凝土结构设计规范[5]中公式计算得到后张法预应力构件短期预应力损失值。由于构件几何特征不同，C-T预应力筋内缩及摩擦损失值远大于V-T，具体数值如表2所示。

表2 短期预应力损失值表 MPa

2.2 数值模型建立

由于储罐罐壁的结构对称性，建立1/4罐壁模型对结构进行模拟。罐壁底部采用固定端约束，两侧截面施加垂直于对称面的轴向约束，罐壁顶端由于上部穹顶及承压环作用施加水平方向的位移约束并施加竖向均布压荷载。ABAQUS建模时采取分离式建模的方法，由于材料属性、结构复杂程度、所需结果不同，不同材料采用不同单元进行模拟，具体单元选取如表3所示。其中设置C-T 99根，V-T 35根；普通钢筋采用Surface面单元[20]模拟，在其Surface面单元Section定义中利用Rebar定义钢筋的间距、横截面积、材料属性及方向。

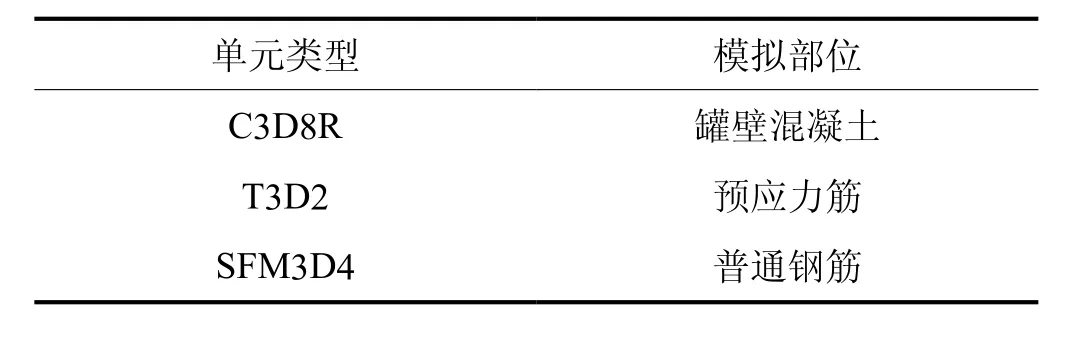
表3 有限元模型单元类型表

混凝土与钢筋均处于线弹性阶段，二者之间黏结良好。采用ABAQUS中自带的Embeded将两者绑定在一起用以模拟混凝土与钢筋的相互作用关系。在初始分析步中采用初始应力法施加初始预应力；分析步1中对结构施加重力、穹顶压力；分析步2中施加预应力筋和混凝土的预定义温度场，模拟C-T和V-T的长期预应力损失。

3 LNG储罐长期预应力损失分析

3.1 长期预应力损失分布

国内大型LNG储罐结构设计基准期为50年，本文取预应力筋张拉后50年作为长期预应力损失计算的终值时间。LNG储罐外罐C-T的50年残余应力分布情况如图2所示。由图2可知，单根C-T沿其长度方向应力变化不大，因此选取各C-T模型中部单元（图2中红色部分），对其应力进行比较，其结果如图3所示。

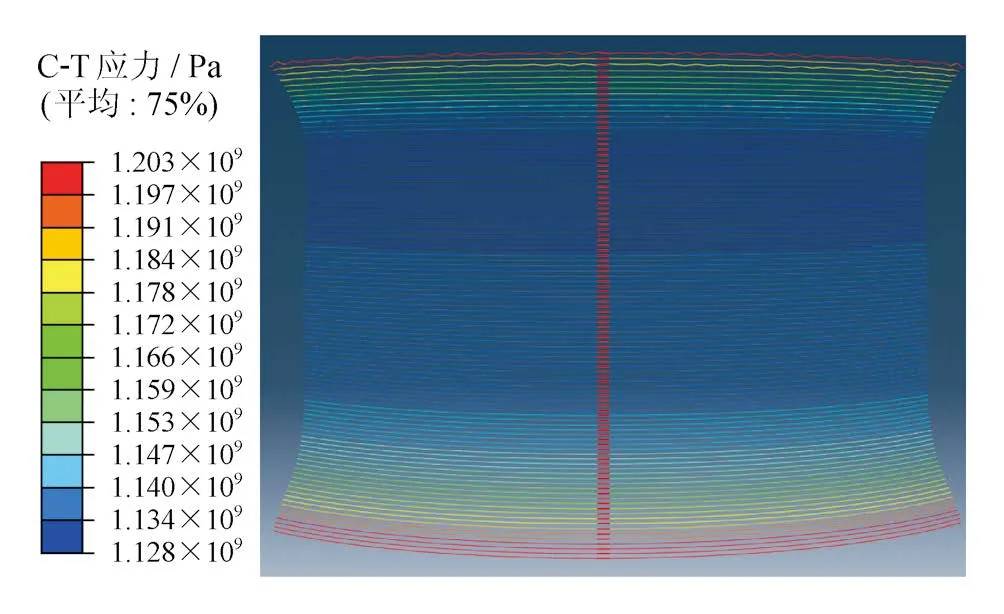
图2 正常使用工况下C-T应力图

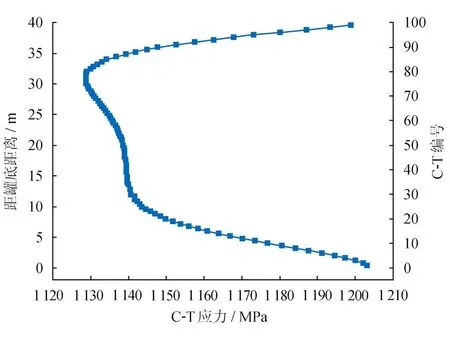
图3 距罐底不同高度C-T应力分布图

由于外罐壁存在穹顶和底板对混凝土环向的约束作用，罐壁顶部和底部C-T长期预应力损失较小。罐壁下部混凝土由于存在较大的混凝土自重作用，产生较大的竖向应力，减小了由C-T作用产生的混凝土环向应变。因此，C-T的长期预应力损失最大值出现在距罐底30.8 m处的77号C-T，其损失终值为162.36 MPa；罐壁底部处的1号C-T长期预应力损失最小，其损失值为92.14 MPa。

不同位置V-T的长期预应力损失值的大小相近。由于重力对混凝土竖向应变的影响，V-T的长期预应力损失自上而下逐渐增大，V-T底部单元长期年预应力损失终值为261.86 MPa。

3.2 收缩徐变损失和应力松弛损失分析

根据C-T及V-T长期预应力损失的分布特点，对模型选取特定单元进行预应力损失分析：C-T选取第77号中部单元，V-T选取最底部单元。分析结果如图4～6所示。

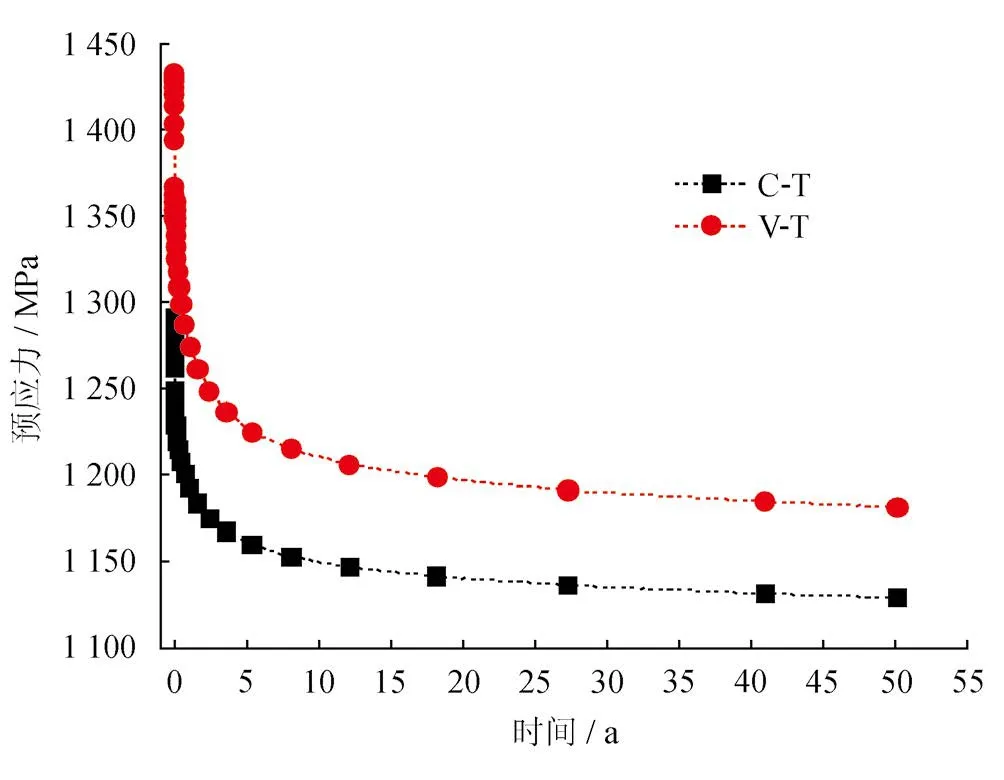
图4 长期预应力损失时变图

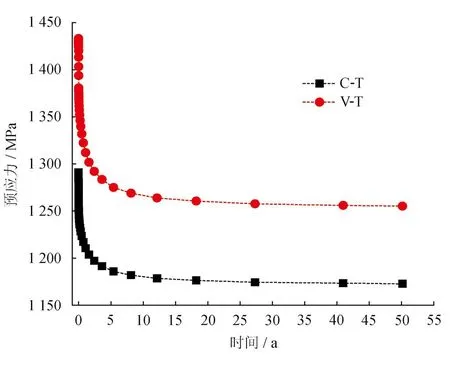
图5 收缩徐变引起的长期预应力损失时变图

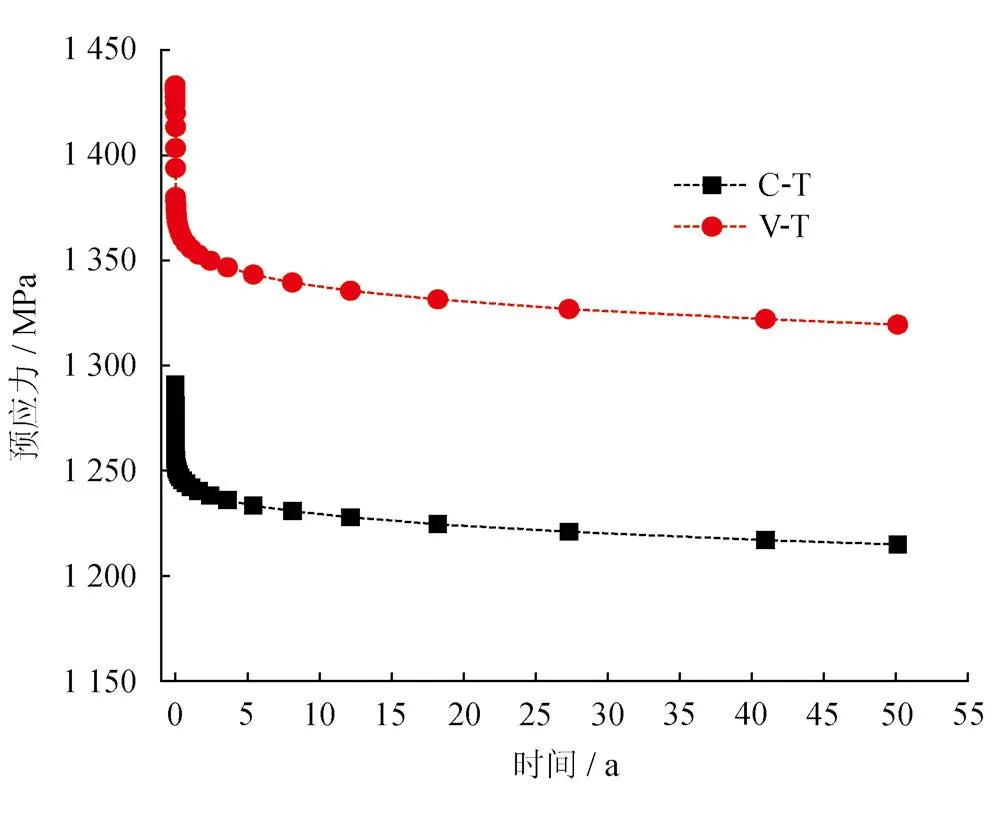
图6 应力松弛引起的长期预应力损失时变图

由图4可知，长期预应力损失在张拉初期变化较为明显，C-T、V-T在5年的长期预应力损失值分别达到损失终值的80.01%、81.71%。由于储罐穹顶仅能够对罐壁混凝土的水平方向产生约束作用，对竖向无约束作用。在穹顶压力、罐壁混凝土自重的作用下，混凝土在竖向将产生额外的徐变变形。因此V-T的长期预应力损失值略大于C-T。

由图5、6可知，由收缩徐变引起的长期预应力损失和由应力松弛引起的长期预应力损失随时间的变化规律与耦合作用下的长期预应力损失规律相近。C-T、V-T由于收缩徐变引起的长期预应力损失终值分别为118.17 MPa和178.01 MPa；由于应力松弛引起的长期预应力损失终值分别为76.07 MPa和113.73 MPa。耦合作用下的长期预应力损失值小于单独计算两项预应力损失的代数和。针对混凝土结构设计规范[5]中预应力损失计算公式，提出相互作用折减系数χ来表示二者间的相互作用：

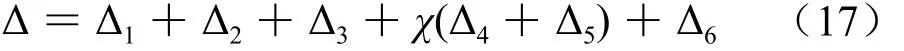
式中Δ表示预应力总损失；Δ1表示锚具变形和预应力筋内缩损失；Δ2表示预应力筋的摩擦损失；Δ3表示混凝土加热养护时，预应力筋与承受拉力的设备之间的温差损失；Δ4表示预应力筋的应力松弛损失；Δ5表示预应力筋由混凝土收缩徐变产生的预应力损失；Δ6表示混凝土的局部挤压损失。

3.3 参数分析

3.3.1 预应力筋的松弛率

C-T、V-T不同松弛率应力松弛损失分别见图7、8。由其可知，松弛率对Δ4影响显著，低松弛预应力筋的Δ4远小于普通预应力筋。当ρ1000为1%时，C-T和V-T的Δ4分别为张拉控制应力（1480 MPa）的3.26%和4.66%；当ρ1000达7%时，C-T及V-T的Δ4分别为张拉控制应力（1 480 MPa）的15.68%和21.51%。由于V-T初始应力较大，V-T的Δ4大于C-T。

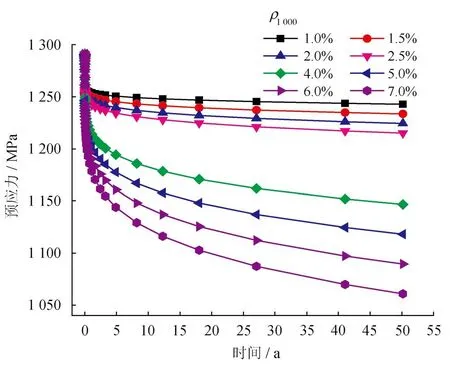
图7 C-T不同松弛率应力松弛损失图

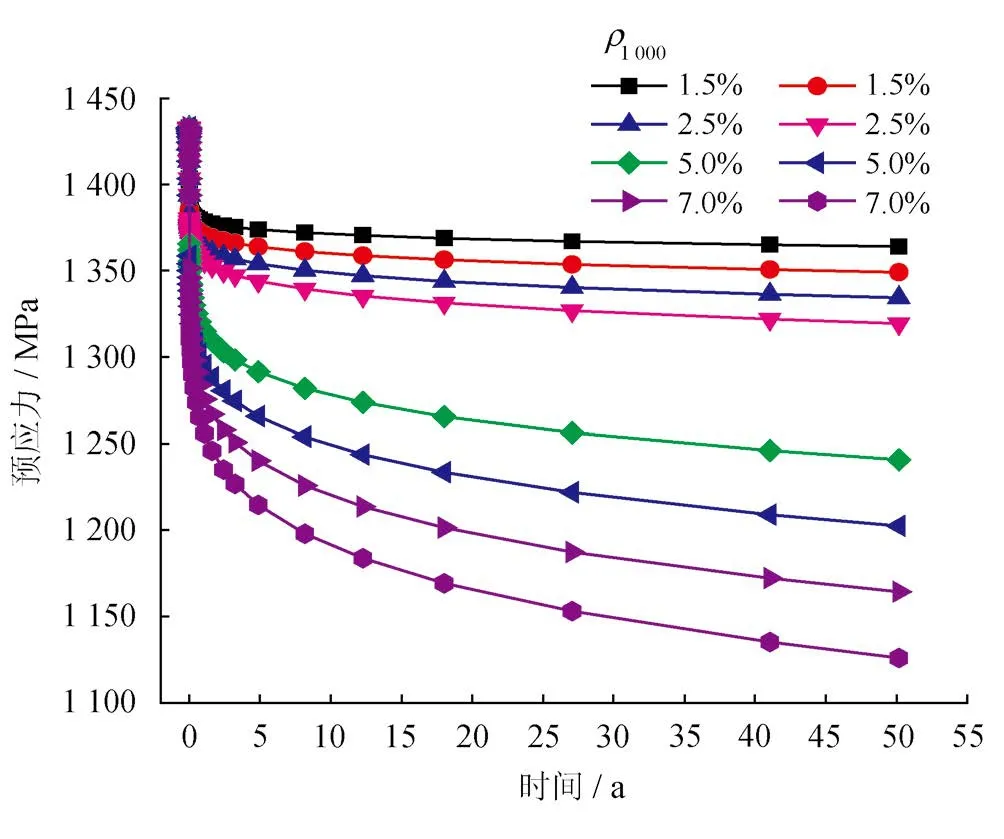
图8 V-T不同松弛率应力松弛损失图

3.3.2 普通钢筋的配筋率

布置普通钢筋可以减小混凝土的收缩徐变，进而减小预应力筋的长期预应力损失。本文通过设置不同的普通钢筋间距，定量分析配筋率（ρrr）对预应力筋长期预应力损失造成的影响（图9、10）。由图9、10可知ρrr对长期预应力损失影响显著，由于普通钢筋能够有效限制由混凝土重力和穹顶压力所产生的竖向应变。因此ρrr对竖向预应力损失值的影响更加明显。

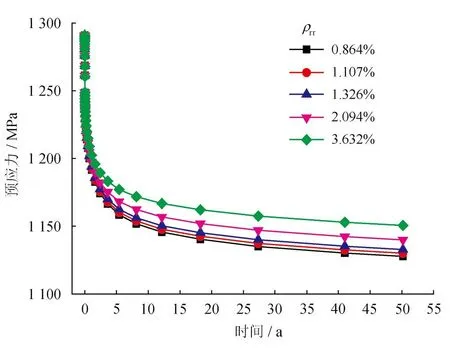
图9 不同配筋率C-T长期预应力损失值图

3.4 相互作用折减系数

相较于其他参数，相互作用折减系数χ受预应力筋的应力松弛损失（Δ4）和由混凝土收缩徐变产生的预应力损失（Δ5）的比值（Δ4/Δ5）的影响最为明显。为了获得χ与Δ4/Δ5之间的定量关系，建立56组模型分别计算其C-T、V-T的Δ4、Δ5及相互耦合作用下的长期预应力损失,结果如图11、12所示。由图11、12可知，χ随Δ4/Δ5的增加呈现先减后增的趋势，当Δ4与Δ5大小相近时χ较小，相互作用较明显。当ρ1000一定时，不同配筋率下χ与Δ4/Δ5在微小变动范围内成正相关。由于构件结构形式及预应力损失水平的影响，V-T的相互作用折减系数总体大于C-T，因此在C-T中，混凝土的收缩徐变和预应力筋的应力松弛二者的相互作用更加明显。

图10 不同配筋率V-T长期预应力损失值图

图11 C-T的相互作用折减系数（χc）随Δ4/Δ5的变化趋势图

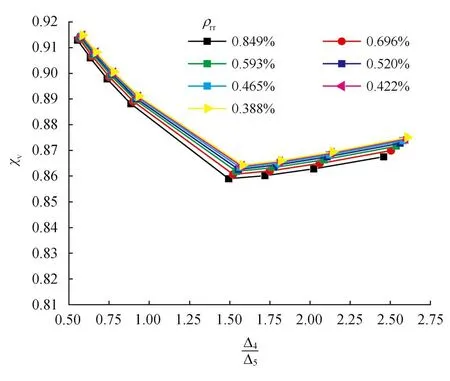
图12 V-T的相互作用折减系数（χv）随Δ4/Δ5的变化趋势图

应用MATLAB拟合出C-T及V-T的 χ随Δ4/Δ5变化的拟合公式。

C-T：

3.5 双向预应力对长期预应力损失的影响规律

图13 单向及双向受力时C-T预应力损失对比图

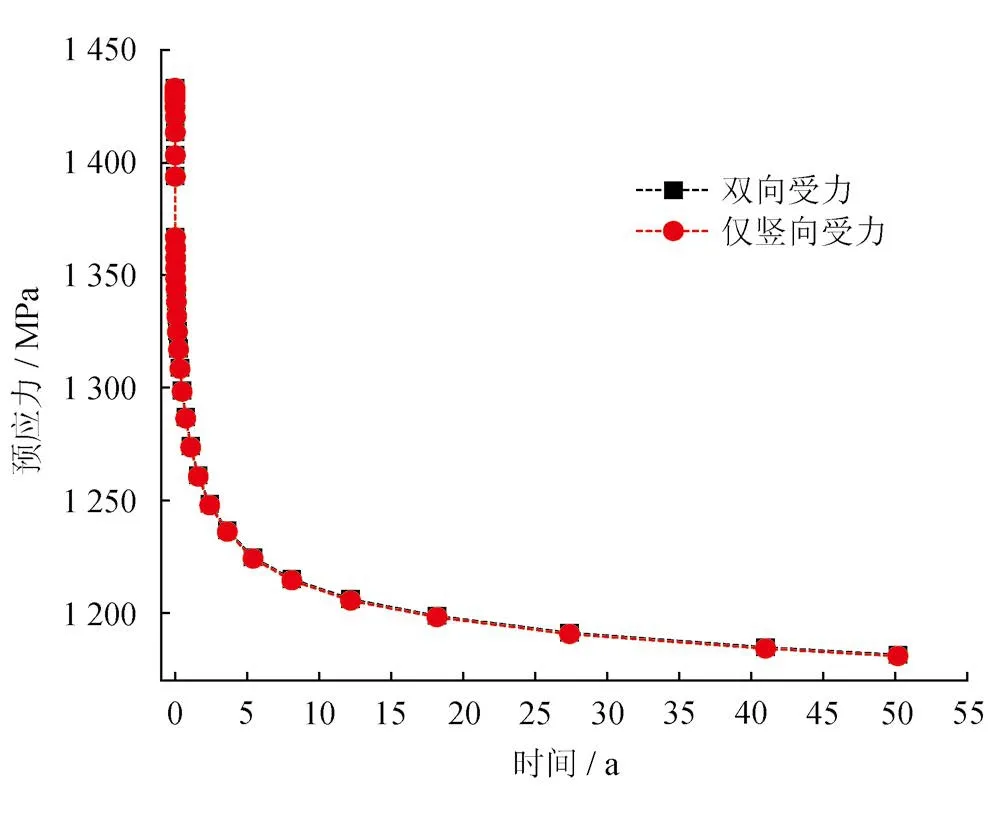
图14 单向及双向受力时V-T预应力损失对比图

单向及双向受力时C-T、V-T预应力损失对比如图13、14所示。由图13、14可知，实际工况下，双向预应力作用时，C-T预应力损失较单向预应力损失值降低2.11%；V-T预应力损失较单向预应力损失值仅降低0.25%。C-T的布置对V-T长期预应力损失的影响较小。

对模型均布设置不同数量的V-T，计算其C-T长期预应力损失终值。C-T损失终值随V-T数量变化如图15所示。由图15可知，C-T预应力损失终值随V-T筋增多呈线性降低的趋势。V-T的布置提供竖向预应力，可降低由C-T产生的混凝土环向应变，进而降低C-T的长期预应力损失值，但相比于降低预应力筋的松弛率和增加普通钢筋配筋率，增加V-T的布置对C-T预应力损失影响较小。

图15 C-T损失终值随V-T数量变化图

4 结论

1）罐壁中上部C-T的长期预应力损失较大，最大值出现在距罐底30.8 m处，其损失终值为162.36 MPa；V-T长期预应力损失自上而下递增，最大值出现在罐壁底部，其损失终值为261.86 MPa。

2）规范中不考虑混凝土收缩徐变与预应力筋应力松弛的相互作用将使长期预应力损失计算结果偏大，针对规范中的相关计算公式，提出相互作用折减系数χ并拟合出相应公式。χ随Δ4/Δ5的增大呈先减后增的趋势，C-T的相互作用折减系数χc小于V-T的相互作用折减系数χv。

3）双向预应力筋的设置对彼此的长期预应力损失存在交互影响，预应力损失值较单向设置预应力时均有所降低。V-T的设置对C-T的长期预应力损失影响更加明显，C-T的长期预应力损失随V-T数量的增加线性减小。