基于分形孔隙模型的含天然气水合物沉积物电阻率数值模拟

陈玉凤 吴能友 梁德青 胡榕华

1.梧州学院化学工程与资源再利用学院 2.自然资源部天然气水合物重点实验室 3.中国科学院天然气水合物重点实验室

0 引言

海底天然气水合物（以下简称水合物）是一种重要的非常规能源，其广泛分布于水深范围为300～1 100 m的大陆架边缘海底的沉积物中[1-2]。电阻率异常法是水合物勘探的一种有效手段，也是估算水合物饱和度的常用方法[3-5]。目前，很多研究者通过实验研究了含水合物沉积物或水合物的电阻率特性[6-9]，影响含水合物沉积物电阻率的因素包括沉积物孔隙度、孔隙水盐度、温度、水合物饱和度以及水合物在沉积物孔隙的分布方式等[10]。

电导模型是通过假设沉积物的孔隙模型，研究多孔介质中孔隙介质导电的微观机理，定量阐明沉积物电阻率与孔隙结构及流体性质、流体分布状态的关系，解决宏观的电阻率测井、岩心实验或室内实验无法准确研究岩心微观孔隙结构、组分等因素对沉积物电阻率具体影响的问题[11]。常见的孔隙模型包括颗粒状模型、毛细管模型、网络模型、格子气自动机模型等。这些模型虽然在岩石物理研究中发挥了一定的作用，但由于对岩石的孔隙结构做了过多的简化处理，不能反映孔隙结构粗糙曲折、剧烈多变的特点，难以考察复杂的微观孔隙结构对其内部导电和流体流动性的影响[12]。对于含水合物沉积物，可借鉴土壤电导模型或含油气沉积物电导模型来模拟含水合物沉积物的孔隙微观结构，确定孔隙介质导电特性与流体饱和度的关系，为含水合物储层饱和度估算提供合适的电导模型。所选用的孔隙模型除了应与沉积物实际孔隙结构较相近，也要考虑到水合物的性质以及水合物在多孔介质的分布方式对沉积物导电的影响。Spangenberg[13]利用均匀颗粒堆积作为孔隙模型，建立了不同分布模式下含水合物沉积物体系的电导模型，指出水合物饱和度指数与颗粒大小、饱和度、粒径分布、孔隙度及胶结指数有关，而不是常数1.938 6，但该研究所使用的均匀颗粒堆积模式与实际多孔介质的复杂孔隙结构有很大的差别，其饱和度模型在实际适用范围有较大局限性。马龙[14]基于数字岩心技术构建反映岩石微观结构的孔隙模型推导了电导模型，研究了含水合物岩心的电阻率与孔隙度、饱和度的关系，由于该研究利用X射线CT扫描岩心得到图像，构建的数字岩心结构固定，难以模拟其他微观因素对岩石物性的影响，这样构建的孔隙介质模型是纯理论上的岩石物理模型，在约束条件较少的情况下可能与实际岩石的孔隙结构存在较大差异[14]。

许多研究者证实了自然界沉积物多孔介质的孔隙结构在一定尺度范围内具有自相似特征[15-17]。分形孔隙模型能很好地准确表征沉积物多孔介质孔隙的复杂结构特征。分形理论广泛应用在土壤、材料等方面。近年来国内外一些学者利用分形孔隙模型研究多孔介质材料的导热系数，多项研究表明该方法是行之有效的[18-24]。笔者基于分形孔隙模型，建立含水合物沉积物的电导模型，并把模型计算结果与实验数据及测井数据进行了对比，分析了孔隙度、孔隙水电导率、沉积物骨架的电导率等因素对含水合物沉积物电阻率与饱和度关系的影响，以期为天然气水合物的资源评估提供理论支持。

1 模型的建立

1.1 分形孔隙模型的建立

自然界的沉积物具有自相似特征，因此可通过构造某些分形结构（如谢尔宾斯基地毯）模拟多孔介质孔隙和固体颗粒的空间构形[16,18]。

谢尔宾斯基地毯的孔隙度（φ）计算公式为：

式中l表示谢尔宾斯基地毯的总边长；c表示谢尔宾斯基地毯的颗粒边长；n表示谢尔宾斯基地毯的阶数。通过改变边长l或c，可以构造具有不同分形维数、不同孔隙度的分形多孔介质。当l和c不发生变化时，孔隙度将随阶数n的改变而改变。因此，通过调整l、c和n来模拟具有不同孔隙度的实际多孔介质。

沉积物多孔介质是由大小不同的颗粒逐渐堆积而成的，这与分形的构造过程相似。拟选定边长l＝3和颗粒边长c＝1的谢尔宾斯基地毯作为沉积物的孔隙模型（图1）。当分辨率较低时，只能发现最大粒径的颗粒，其他面积暂时是孔隙，随着分辨率的增大，小一级的颗粒不断被发现，实际孔隙面积不断减小，粒径大小各异的多孔介质颗粒不断填充孔隙空间[25]。用l（l＝3）表示观测总范围，即地毯的总边长；c（c＝1）为观测尺度，即颗粒粒径（颗粒边长），当用l的观测尺度去观测时，只能发现粒径大于或等于c的颗粒[26-27]。

1.2 电导模型的建立

根据双弥散多孔介质模型，沉积物颗粒是由随机分布不相接触的颗粒和具有自相似分布相互接触的颗粒组成，后者是颗粒之间存在接触电阻[15]。

用谢尔宾斯基地毯模拟具有自相似分布的接触颗粒，假设含水合物沉积物是由沉积物颗粒骨架、天然气水合物、孔隙水3个部分组成。根据等效电阻网络，建立含天然气水合物沉积物的电导模型（图2）。图2中的黑色部分代表沉积物多孔介质骨架（颗粒），其电导率为σs；灰色部分代表孔隙水，其电导率为σw；白色部分代表固态的天然气水合物，其电导率为σg。孔隙水饱和度（Sw）为两个部分：环绕颗粒周围的水饱和度（Swsp）和颗粒之间存在的接触电阻的水饱和度（Swb）。

图1 分形孔隙模型图

图2 含天然气水合物沉积物的分形孔隙模型和电阻网络图

根据含水饱和度的定义：

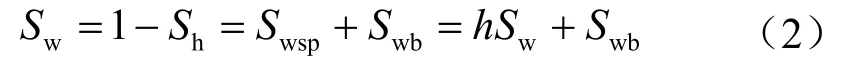
式中Sw表示含水饱和度；Sh表示水合物饱和度；h表示经验常数。h＝Swsp/Sw，0≤h≤1，当h＝1，所有的水围绕在颗粒周围，即所有的颗粒都处于非接触状态；当h＝0时，所有的颗粒都处于接触状态；对于含天然气水合物沉积物，h经验取值范围为0.4 ～ 0.9[28]。

日子一天天过去，我自以为与叶霭玲的关系是虚的，与白丽筠的关系才是实的，有着实质性内容。但是，就像性生活不能公之于众那样，我与白丽筠的关系也是放不上台面的。相反，我与叶霭玲的关系却有两家的父母亲属做见证，有着不容怀疑的社会属性。因而事实上，我与叶霭玲的关系才是实的，与白丽筠反倒是虚的。

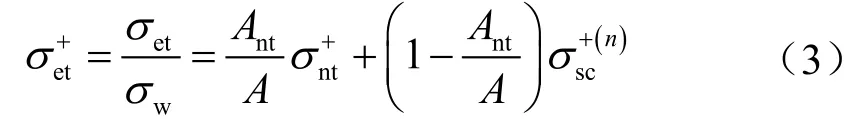
式中σet表示沉积物多孔介质的总电导率；σw表示孔隙水的电导率；Ant/A表示不相接触的颗粒占全部颗粒的体积分数；(1－Ant/A)表示自相似分布相互接触颗粒占全部颗粒的体积分数，0＜Ant/A＜1，Ant/A≈φ[20]；σ+nt是非接触颗粒的等效电导率；σ+(n)sc是接触颗粒的n阶等效电导率。其中上标n（＝0，1，2，…，n）代表谢尔宾斯基地毯的阶数。

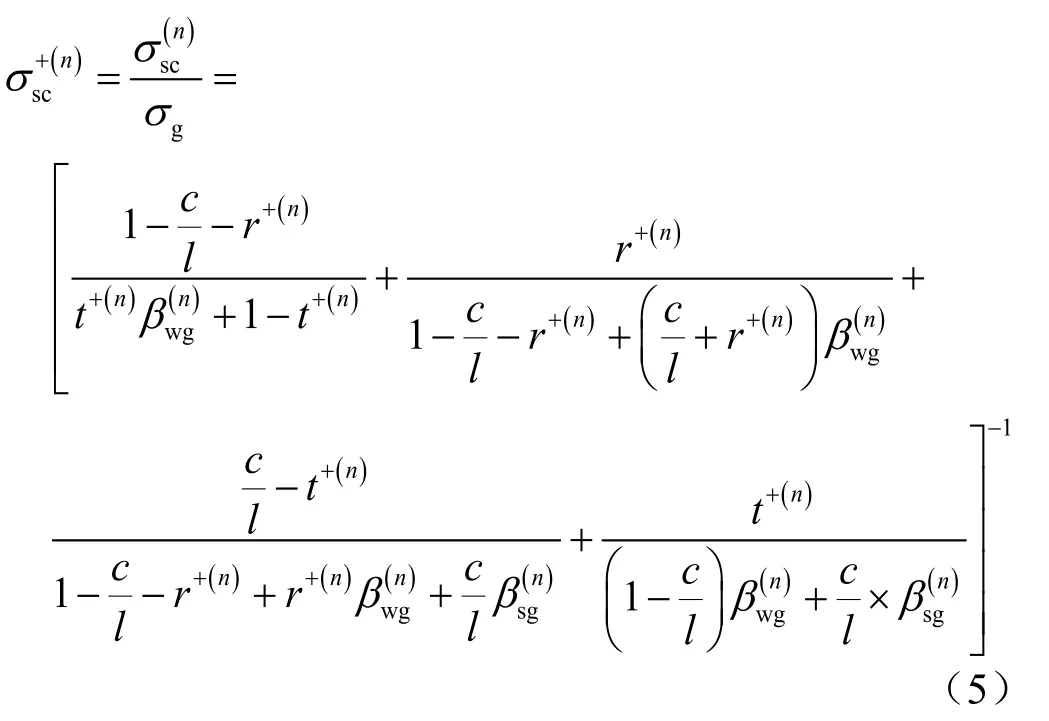
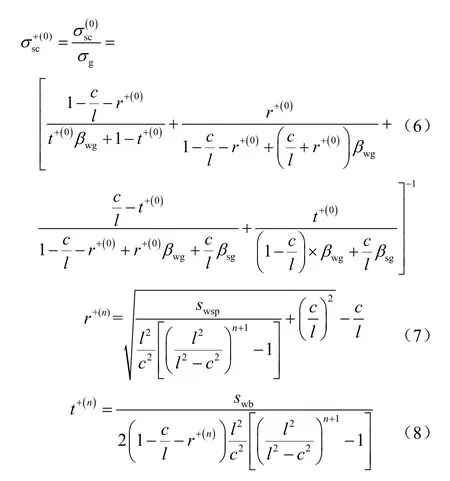
公式（3）是用严格自相似分形几何结构体（谢尔宾斯基地毯）模拟自相似分布的颗粒，对于实际多孔介质，需要引入经验参数i对颗粒无序分布的程度进行修改，实际多孔介质的总有效电导率为：

式中经验参数i表示实际多孔介质的无序程度，取值范围为1.0～2.0[29]。

则含水合物沉积物的电阻率（ρt）为：

式中ρo表示水饱和沉积物的电阻率。

在电导模型中，含水合物沉积物的电阻率（ρt）可表示为孔隙度（φ，由l、c和n确定）、水合物饱和度（Sh）、各部分介质（沉积物骨架、孔隙水和天然气水合物）的电导率、经验常数（i，与沉积物随机、无序的结构有关）和h（与颗粒的接触状态有关）、以及孔隙微结构尺寸（l和c）的函数。对于盐水—水合物—多孔介质骨架体系，根据GMGS1的测井数据，确定σw的范围为5.00～2.85 s/m（由盐度和温度确定）[30]；多孔介质骨架主要成分为石英砂时，其电导率（σs）的取值范围为10－8～10－16s/m，对于含有黏土的多孔介质骨架，其σs的取值范围为5×10－2～2 s/m；天然气水合物的电导率（σg）为10－6s/m；在计算中，选取经验参数i、h，可以获得含水合物沉积物电阻率与饱和度的关系[28-29]。

2 结果与讨论

2.1 含水合物海砂沉积物电阻率数值模拟

图3给出了ρt的模拟数值与实验数据的比较。实验采用的海砂样品来自南海神狐海域的浅层，其主要成分为二氧化硅，不含黏土矿物，粒径介于60～100 目（0.154～0.28 mm）。有关含水合物海砂沉积物的电阻率的实验测量方法见本文参考文献[8]。在计算中，选取参数σs＝10－14s/m，σw＝3.3 s/m，l＝ 3，c＝ 1，φ＝ 0.39，Ant/A＝ 0.33，i＝ 1.83，h＝0.75。从图3可以看出，在水合物饱和度0～0.6的范围内，该模型的模拟结果与实验数据值吻合较好。

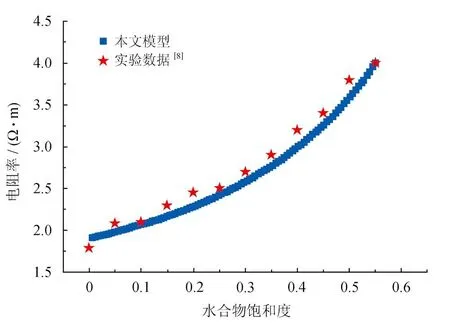
图3 含水合物海砂沉积物电阻率的数值模拟结果与实验数据[8]的比较图

2.2 含水合物岩心电阻率数值模拟

图4 给出了含水合物岩心电阻率（ρt）的模拟数值与电阻率测井数据的比较，岩心沉积物样品主要由未固结的（含）钙质生物的黏土质粉砂和（含）钙质生物粉砂组成[30]。有关南海神狐海域SH7B站位含水合物岩心电阻率测井曲线和水合物饱和度值见本文参考文献[30]。计算中选取参数σs＝0.1 s/m，σw＝4.3 s/m，l＝3，c＝1，n＝7，φ＝0.44，Ant/A＝0.44，i＝ 1.52，h＝ 0.3。从图 4可以看出，SH7B站位含水合物层段的电阻率测井数据范围为1.75～3.00 Ω·m，水合物饱和度范围为0～43%。总体上，本模型模拟数值与实地测井数值一致，这也验证了本模型的有效性。

2.3 电阻率增大指数与水合物饱和度关系的模拟

图5给出了本模型全饱和度范围内双对数坐标系下含水合物海砂电阻率增大指数（I）与水合物饱和度（Sh）关系曲线。在计算中，选取模型参数σs＝10－14s/m，σw＝3.3 s/m，l＝3，c＝1，φ＝0.39，Ant/A＝0.39，i＝1.83，h＝0.75。其中，模型采用的孔隙度由实验测量海砂样品得到，Ant/A≈φ[20]，h的取值见本文参考文献[28]，i的取值见本文参考文献[29]，下同。

从图5看出， I随着Sh的增大而增大；当Sh较高（大于50%）时，I（沉积物的电阻率）急剧增大。

2.4 孔隙度、孔隙水电导率和沉积物骨架电导率对含水合物沉积物电阻率的影响

采用单因素分析法研究了孔隙度（φ）、孔隙水电导率（σw）和沉积物骨架电导率（σs）对含水合物沉积物电阻率（ρt）的影响，如图6所示，其中φ、σw、σs值均来自于测井数据[30]，其余模型参数取值如表1所示。

图4 含水合物岩心电阻率的数值模拟结果与电阻率测井数据[30]的比较图

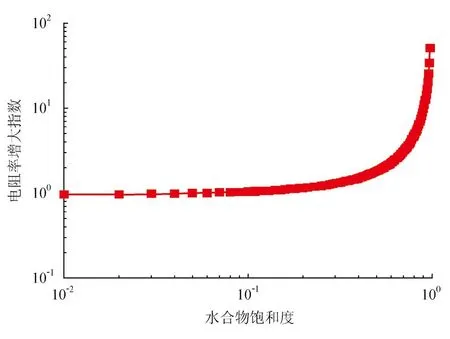
图5 2.8 ℃下含水合物海砂电阻率增大指数与水合物饱和度的模拟关系图

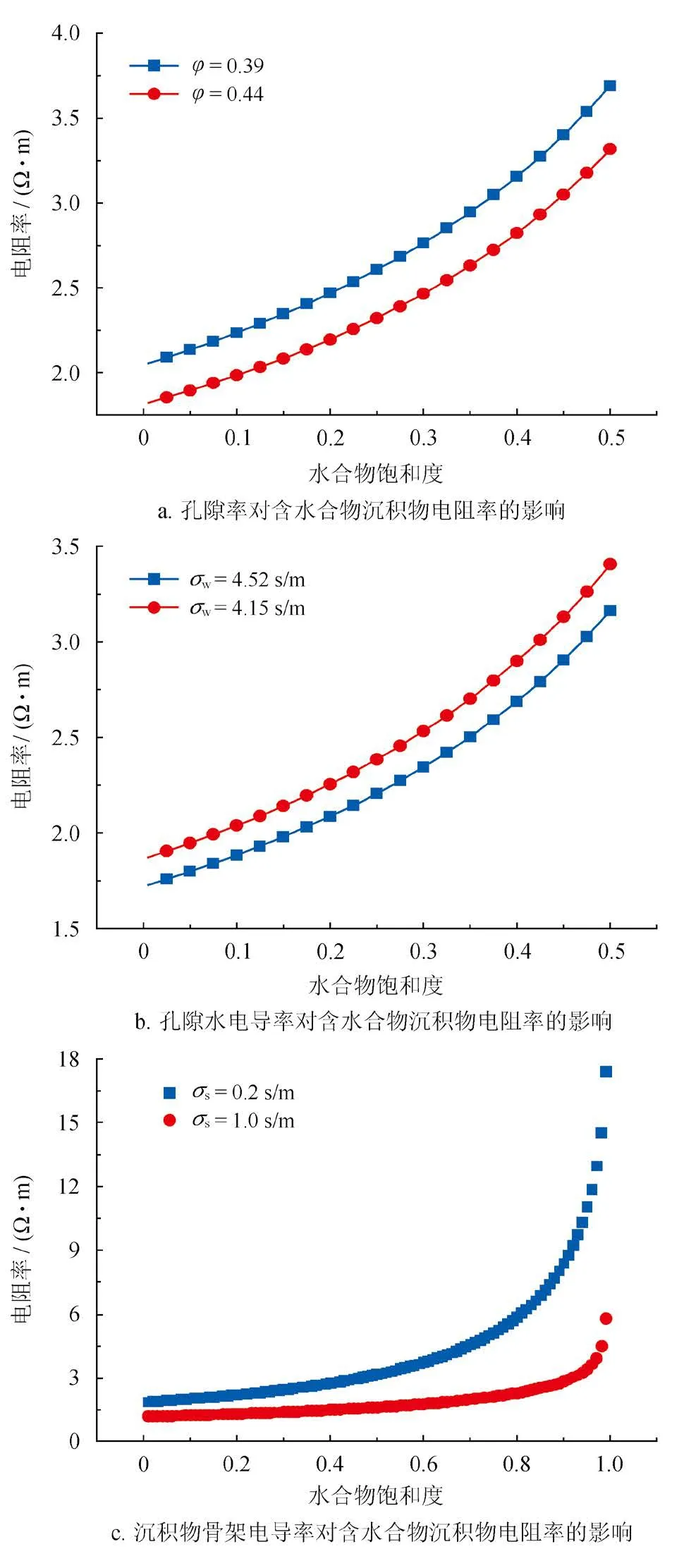
图6 孔隙度、孔隙水电导率和沉积物骨架电导率对含水合物沉积物电阻率的影响图

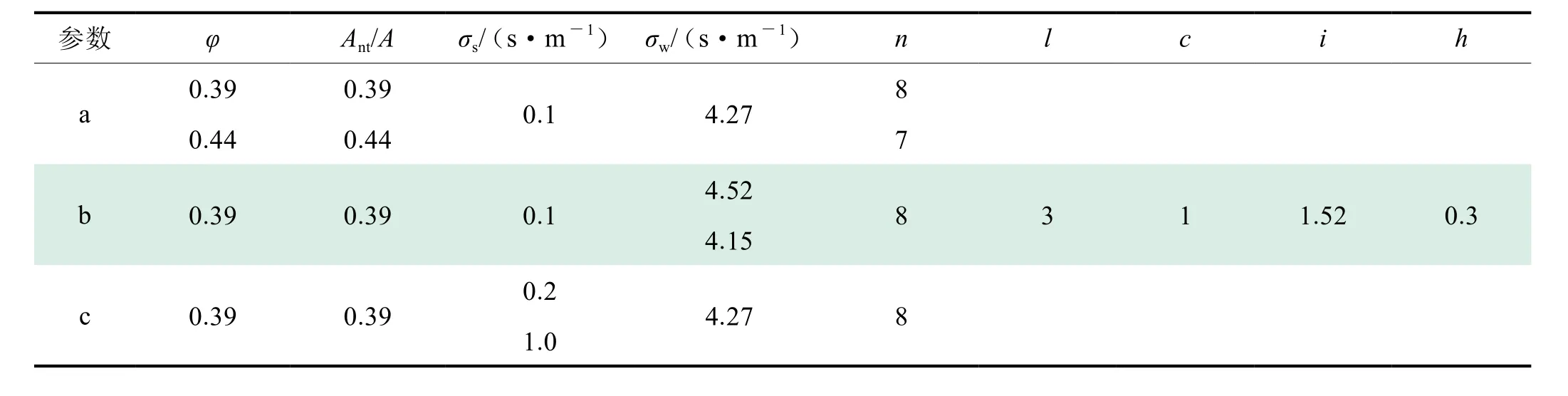
表1 含水合物沉积物电阻率的电导模型参数表

从图6-a中可以看出，在水合物饱和度小于50%时，ρt随着φ的减小而增大；在图6-b中，当σw减小时，ρt增大；在图6-c中，σs对ρt的影响较大，在高水合物饱和度范围内，ρt随σs的增大而明显减小。这是由于沉积物的黏土含量越高，沉积物颗粒骨架的电导率越大。因此，对于含有黏土的沉积物，含水合物的沉积物受黏土附加导电性的影响较大。

3 结论

1）基于自然界中沉积物多孔介质具有统计自相似的特征及等效电阻网络模式，选取地毯总边长l＝3，颗粒粒径c＝1的谢尔宾斯基地毯为分形孔隙模型，建立了含天然气水合物沉积物的电导模型。

2）所建立的模型，含天然气水合物沉积物的电阻率可以表示为孔隙度（与阶数n有关）、面积比、微观结构尺寸、孔隙水电导率（由盐度和温度确定）、沉积物骨架电导率（由黏土含量确定）和经验参数的函数。在一定的范围内，该模型的模拟结果与实验数据和测井数据都能较好地吻合。

3）在验证该模型有效性的基础上，利用模型推广了较宽水合物饱和度范围内的沉积物电阻率增大指数（I）与水合物饱和度（Sh）的关系：随着孔隙度（φ）的减小，沉积物的电阻率增大；而沉积物的电阻率随着孔隙水电导率的减小而增大；在高水合物饱和度范围内，沉积物的电阻率随着沉积物颗粒骨架电导率的增大而明显减小。