高温作业专用服装设计

赵峰禹 何庆伟 赵小程

摘要：为了解决在高温作业环境下，为了使工作人员可以更好的进行工作。必须解决在不同温度环境下，高温作业服装每层厚度的确定。针对不同的外界温度在给定每层不同的厚度。利用假人进行皮肤表层温度测定。根据假人皮肤外侧的实际温度，得到温度分布图像，建立出假人皮肤外侧温度与所处环境时长的数学函数。需要解决在不同的环境温度下针对每层不同的厚度，不同的工作时间，来确定每层的最优厚度。利用了一维数学模型，将其看成是单位面积的不同厚度的分析，从而确定优化问题。

关键词：热传导；最优厚度；温度分布

1、模型建立

根据所给的参数进行分析，可以将每一层的材料看成不同的热阻（设有四层不同的材料）。将高温专用服装看成一个单位面积的服装，但存在厚度的变化，利用Laplace变换导出的公式对于单层的材料有两侧温差与该层吸收热量的方程。利用热传导有限元法，将有限单元法应用到高温作业服的温度效应计算，提出了计算服装不同层厚度的公式。[1]

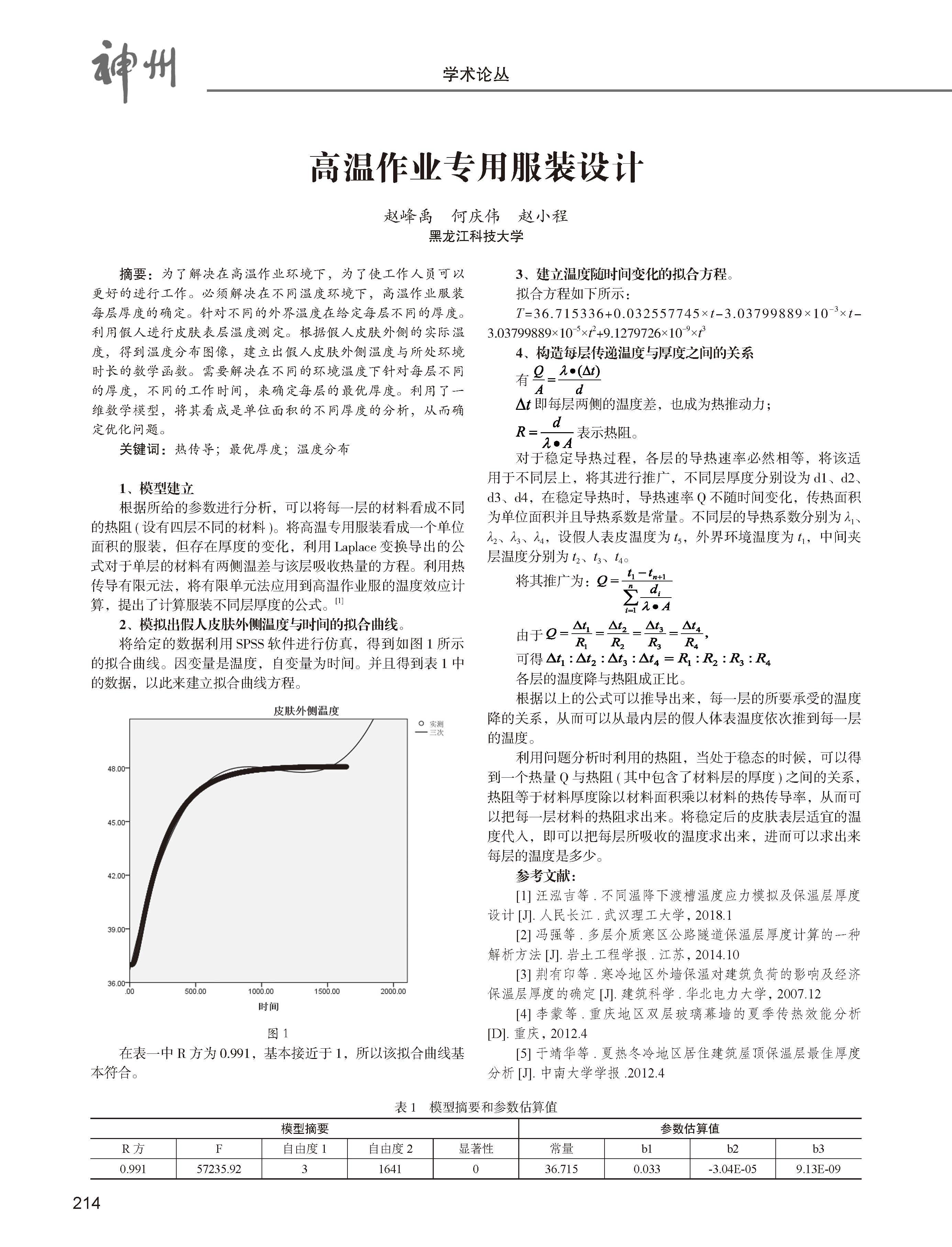
2、模拟出假人皮肤外侧温度与时间的拟合曲线。

将给定的数据利用SPSS軟件进行仿真，得到如图1所示的拟合曲线。因变量是温度，自变量为时间。并且得到表1中的数据，以此来建立拟合曲线方程。

在表一中R方为0.991，基本接近于1，所以该拟合曲线基本符合。

3、建立温度随时间变化的拟合方程。

拟合方程如下所示：

T=36.715336+0.032557745×t-3.03799889×10-3×t-3.03799889×10-5×t2+9.1279726×10-9×t3

4、构造每层传递温度与厚度之间的关系

有

即每层两侧的温度差，也成为热推动力；

表示热阻。

对于稳定导热过程，各层的导热速率必然相等，将该适用于不同层上，将其进行推广，不同层厚度分别设为d1、d2、d3、d4，在稳定导热时，导热速率Q不随时间变化，传热面积为单位面积并且导热系数是常量。不同层的导热系数分别为λ1、λ2、λ3、λ4，设假人表皮温度为t5，外界环境温度为t1，中间夹层温度分别为t2、t3、t4。

将其推广为：

由于

可得

各层的温度降与热阻成正比。

根据以上的公式可以推导出来，每一层的所要承受的温度降的关系，从而可以从最内层的假人体表温度依次推到每一层的温度。

利用问题分析时利用的热阻，当处于稳态的时候，可以得到一个热量Q与热阻（其中包含了材料层的厚度）之间的关系，热阻等于材料厚度除以材料面积乘以材料的热传导率，从而可以把每一层材料的热阻求出来。将稳定后的皮肤表层适宜的温度代入，即可以把每层所吸收的温度求出来，进而可以求出来每层的温度是多少。

参考文献：

[1]汪泓吉等.不同温降下渡槽温度应力模拟及保温层厚度设计[J].人民长江.武汉理工大学，2018.1

[2]冯强等.多层介质寒区公路隧道保温层厚度计算的一种解析方法[J].岩土工程学报.江苏，2014.10

[3]荆有印等.寒冷地区外墙保温对建筑负荷的影响及经济保温层厚度的确定[J].建筑科学.华北电力大学，2007.12

[4]李蒙等.重庆地区双层玻璃幕墙的夏季传热效能分析[D].重庆，2012.4

[5]于靖华等.夏热冬冷地区居住建筑屋顶保温层最佳厚度分析[J].中南大学学报.2012.4