小数据量矢量地理数据水印算法
佟德宇,朱长青,任 娜
1. 南京师范大学虚拟地理环境教育部重点实验室,江苏 南京 210023; 2. 江苏省地理环境演化国家重点实验室培育建设点,江苏 南京 210023; 3. 江苏省地理信息资源开发与利用协同创新中心,江苏 南京 210023
矢量地理数据具有空间特征明显、精度高、组织结构多样的特点,其中小数据量的矢量地理数据例如矢量切片、区域采样点、矿井分布、军事敏感区等,在数据共享和分发中面临着盗版、侵权和泄密等安全问题,迫切需要有效的技术手段进行安全保护和版权鉴定。数字水印技术将版权信息与数据紧密结合,能够有效实现矢量地理数据的版权保护、追踪溯源和安全管理。目前矢量地理数据水印算法已取得较多研究成果,根据嵌入域的不同可分为空间域、频率域及几何域的水印算法。空间域水印算法运用量化、坐标映射等方法,直接对矢量数据坐标嵌入水印,实现较强的抵抗增删攻击的能力[1-5];频率域水印算法将水印嵌入至坐标变换域系数中,例如离散傅里叶变换、离散余弦变换等,提升了算法抗噪声、平移等攻击的能力[6-12];基于几何域的水印算法将水印嵌入至地理数据几何特征中,包括角度、距离、弧长等,能够对旋转、缩放、平移等几何攻击具有更好的抵抗性[13-18]。
综合来看,现有的矢量地理数据水印算法研究侧重于稳健性的提升,但对水印容量方面研究较少,大多数水印算法对每个节点嵌入的水印容量不超过2 bit[1-18]。但在实际中,小数据量的矢量地理数据往往只有100个节点左右,而水印信息长度可超过1000位。例如,一幅32×32像素的二值版权图像的信息量为1024 bit。因此,高水印容量的需求与载体小数据量的特性矛盾明显,现有的水印算法难以对小数据量数据进行有效的水印嵌入和检测。
本文针对水印算法容量较低的问题,提出一种适用于小数据量的矢量地理数据水印算法。在水印生成阶段,通过压缩感知并构建量化表,减小水印信息的长度和冗余;水印嵌入时,增加量化区间数量以提高单位节点嵌入的水印容量,对节点形成的夹角进行多段量化调制,从而既保证对增删攻击和几何攻击具有一定的稳健性,也能够提高小数据量数据中嵌入的水印容量。
1 水印信息的稀疏采样和量化
水印算法的主要步骤包括水印信息生成、嵌入和检测。其中水印信息生成方法包括有意义版权图像的获取、水印信息的置乱或者加密等[4,19-20]。加密或者置乱的方法能够提高水印算法的安全性,但不能显著地压缩水印信息。因此为提高水印嵌入容量,需要对二值版权图像进行压缩,降低图像的冗余性。
压缩感知作为一种信号处理的新兴方法,能够以较低的采样率测量信号并稳健重构信号[21-22]。它的原理是当数据在特定域φ中稀疏表示时,用与φ不相关的矩阵对数据进行欠采样,获得测量结果的同时实现数据压缩;恢复和重构信号时,虽然欠定方程组理论上没有确定解,但根据原始信号在φ中稀疏的性质,通过优化算法或者贪婪算法能够重构原始信号,并在一定程度上抵抗噪声、信号丢失的攻击[23]。因此,在水印信息生成中运用压缩感知方法,能够在压缩水印信息的同时增加水印信息重构过程中的稳健性。同时,测量矩阵作为密钥也可以保证水印的安全性[24]。
运用压缩感知对二值图像水印信息进行测量时,测量结果的数值范围往往超过(-1,+1),并含浮点型数值,直接转换为二值水印信息反而会大幅增加水印信息长度。为实现水印信息的压缩和准确重构,本文提出了压缩感知和量化机制相结合的水印信息生成算法,对压缩感知的测量值进行量化调制,有效压缩水印信息量并保证其恢复的准确性。
基于压缩感知和量化机制的水印信息生成步骤为:
(1) 获取大小为L×L的二值版权图像W。
(2) 对二值版权图像W进行分块,分块大小为N×N,对各块进行小波分解,实现图像的稀疏化表达。
Yb=ΦWb
(1)
式中,Yb为图像各分块的测量结果。
(4) 对测量结果Yb进行取整量化,为计算方便,建立量化表将测量结果映射为量化值,量化表如表1所示。

表1 测量结果量化表
式中,WMi∈{-2,-1,1,2}。
2 角度多段量化规则


图1 可嵌角度调制过程Fig.1 The process of quantization modulation on angle

(2)
对于角度α,设多段量化区间的单位角度为θ,嵌入水印信息WMi时,首先计算角度α对应的量化区间索引值R为
(3)

(4)
式中,α′为嵌入水印后的角度值,从而实现角度的多段量化调制。
3 水印算法
3.1 误差控制策略

3.2 水印嵌入
水印嵌入算法在水印信息稀疏采样和量化基础上,运用角度多段量化机制、动态更新方式对矢量地理数据的夹角嵌入水印,具体嵌入步骤为:
(1) 根据基于压缩感知和量化表的水印信息生成方法,生成水印信息WM,保存水印信息生成过程中的测量矩阵Φ,作为水印检测的密钥。
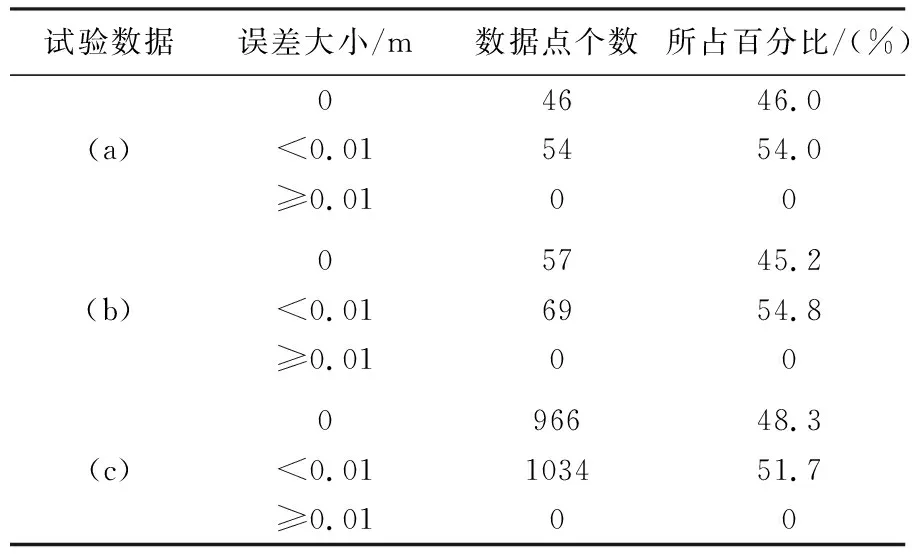
(2) 依据第2节中可嵌角度的选取规则,读取矢量地理数据并获取所有可嵌角度,记为∠PkPk+1Pk+2(0≤k (3) 从第一个可嵌角度∠PkPk+1Pk+2开始,根据三点的坐标计算对应的角度αk。 (5) (6) 水印检测是水印嵌入的逆过程,水印检测时根据角度所在的量化区间判断水印值,对检测出的水印值进行压缩感知重构,从而恢复原始水印。水印检测步骤为: (7) (8) (6) 基于密钥Φ,运用正交匹配追踪法重构版权图像[25],完成水印检测。 水印算法的有效性从数据可用性、水印容量和稳健性3个方面进行试验验证。试验数据如图2 所示,图2(a)和(b)各为小数据量的点数据和线数据,图2(c)为普通数据量的面数据,所含有的节点个数分别为100个、126个和2000个,比例尺分别为1∶2000、1∶5000和1∶10 000。 水印信息为32×32像素的二值版权图像,如图3所示。 (9) 式中,Nwm为水印长度;XNOR为异或运算。当NC=1时,表示水印检测完全正确,当NC=0时,表示完全未检测出水印。 本文主要分析了双绕组电力变压器集总参数模型,构建了串联阻抗支路矩阵和并联导纳支路矩阵,再基于基尔霍夫电流和电压定律来获取支路电流与节点电压之间的关系;同时分析了变压器绕组径向变形和轴向位移故障时的主要影响参数,以期为后续系统研究变压器绕组故障提供相关的理论基础。 在未攻击的情形下对水印进行检测,水印检测结果如表2所示。 图2 试验数据Fig.2 Experimental data 图3 二值版权图像Fig.3 Binary copyright image 试验数据数据(a)数据(b)数据(c)节点个数1001262000水印检测图像NC0.56480.81951 从表2中可以看出,对于含有100个和126个节点的小数据量数据(a)和数据(b),检测结果与原始水印存在部分像素差异,但是图像内容可辩,能够明确反映出版权标识,且NC均高于0.5;对于含2000个节点的数据(c),无论是视觉上还是NC值都表明检测出的水印图像与原始水印完全一致。上述试验结果表明,提出的水印算法能够对小数据量的数据嵌入较为完整的水印信息,也适用于较大数据量数据的水印嵌入和检测。 为验证水印算法对矢量地理数据精度和可用性的影响,统计试验数据在水印嵌入后的误差,统计结果如表3所示。 表3 误差分析 从表3可知,嵌入水印后坐标误差均能够控制在0.01 m之内,满足不同比例尺下矢量地理数据精度要求,这是因为在水印嵌入时,角度动态更新方法和较小的参数θ严格控制了数据误差,避免角度调制过程引起坐标数值的大幅变化。因此本文提出的水印算法能够保证矢量地理数据的可用性。 为验证水印算法的嵌入容量,对不同数据量的数据嵌入和检测水印,验证检测结果的正确性并计算单个节点嵌入的水印容量。 首先对试验数据(a)和(b)进行不同程度的增删点预处理,生成不同数据量的数据,嵌入的水印信息统一为图3所示的二值版权图像,水印信息量为1024 bit。对比试验算法为稳健性较好的文献[4](算法1)和文献[18](算法2),分别从主观视觉和客观指标方面评价水印检测的结果。在计算嵌入容量时,式(9)中未检测到的水印位XNOR计算结果为0。小数据量数据(a)和(b)的水印检测结果如表4和表5所示。 表4 小数据量数据(a)水印检测结果 表5 小数据量数据(b)水印检测结果 在小数据量数据试验基础上,根据嵌入的总水印容量和节点个数,计算单个节点嵌入的水印容量。取上述试验的平均值作为衡量水印算法容量的指标,结果如表6所示。 表6 水印算法容量比较 由表4和表5可知,对于相同数据量的试验数据,本文水印算法的检测结果无论是视觉上还是相关系数NC,均优于对比算法;并且数据量越小,检测结果的差异性也越明显。极限情况下对仅含100个节点的矢量地理数据,本文的算法仍然能成功嵌入水印并检测,检测结果视觉可辩,版权归属明确,且相关系数NC保持在较高的水平;相同条件下算法1和算法2难以完整地嵌入水印,版权信息辨识度低,无法鉴定小数据量的版权归属。从表6的结果可以看出,本文水印算法的单个节点水印容量高于对比算法,每个节点能够承载的水印位数得到较大提升。因此,试验证明本文提出的水印算法有效地提高了水印容量,能够满足小数据量矢量地理数据版权保护的需求。 为验证水印算法抵抗各类攻击的能力,分别对普通数据量的数据(c)和小数据量数据(b)进行稳健性试验,嵌入水印并对矢量地理数据进行增删攻击和几何攻击,对比水印检测结果的NC值,从而评价本文算法和算法1、算法2的稳健性。根据表4和表5的试验结果可设置经验阈值T=0.5,即NC<0.5时版权归属难以分辨,此时试验结果记为“×”,表明水印未成功检测。基于普通数据量数据(c)的稳健性试验结果如表7所示。 表7 普通数据量水印算法稳健性 由表7可知,对于普通数据量的数据,本文算法和对比算法都能完全抵抗几何攻击;但本文算法由于水印容量高,因此在抵抗增删攻击方面具有更好的稳健性。对于节点排序攻击,线数据和面数据的拓扑关系未改变,点数据经坐标排序后的顺序也未改变,因而水印算法能完全抵抗节点排序攻击。 基于小数据量数据(b)的稳健性试验结果如表8所示。 表8 小数据量数据水印算法稳健性 由表8可知,对于小数据量的数据,算法1和算法2的水印容量较低,无法完整地嵌入二值版权图像水印信息,更难以抵抗任意程度的增删、平移、旋转等攻击。而本文提出的水印算法由于使用了压缩感知、角度多段量化等机制,提高了水印嵌入容量,能够完全抵抗平移、旋转、缩放等几何攻击和节点排序攻击,也能较好地抵抗增删攻击。因此,本文的水印算法不仅能对小数据量数据嵌入水印,同时保证了良好的稳健性。 针对小数据量矢量地理数据的版权保护需求,本文提出了一种高水印容量的水印算法。水印生成阶段,运用压缩感知进行测量并量化测量结果,在保证水印信息稳健重构的基础上实现了水印信息的压缩;水印嵌入阶段,提出角度的多段量化规则,进一步提升了单个节点能承载的水印容量,也提高了算法的稳健性。试验结果表明,提出的水印算法能够在小数据量的矢量数据中嵌入和检测水印,检测结果版权意义明确,单个节点嵌入的水印容量高于现有的水印算法,同时算法对增点、删点、缩放、旋转、裁切、排序等攻击也具有很好的稳健性。本文研究有效地解决了矢量数据的小数据量与水印容量的矛盾,实现了小数据量矢量地理数据的水印嵌入和检测,对矢量地理数据的版权保护具有重要的理论和应用价值。

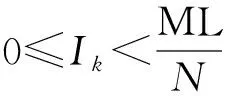

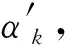

3.3 水印检测




4 试验与分析




4.1 数据可用性
4.2 水印容量
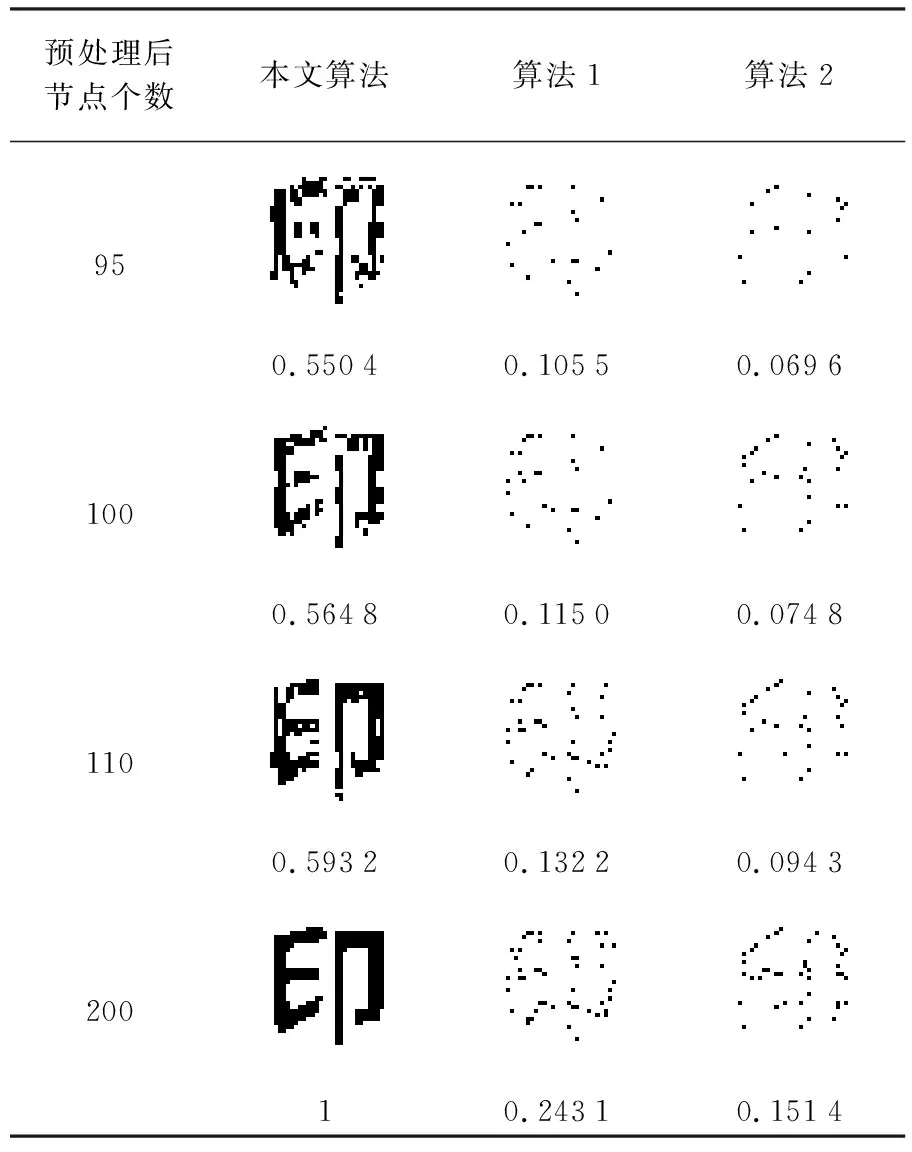
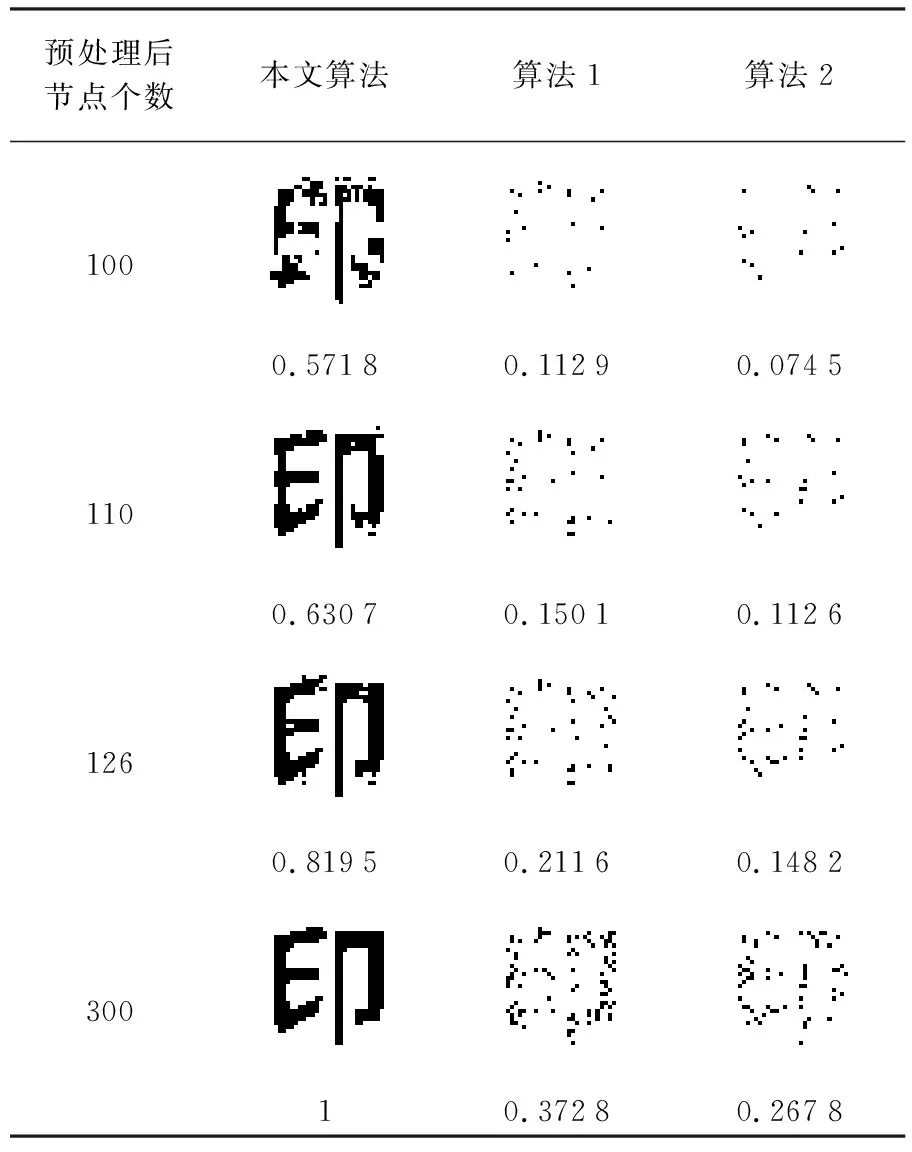

4.3 稳健性

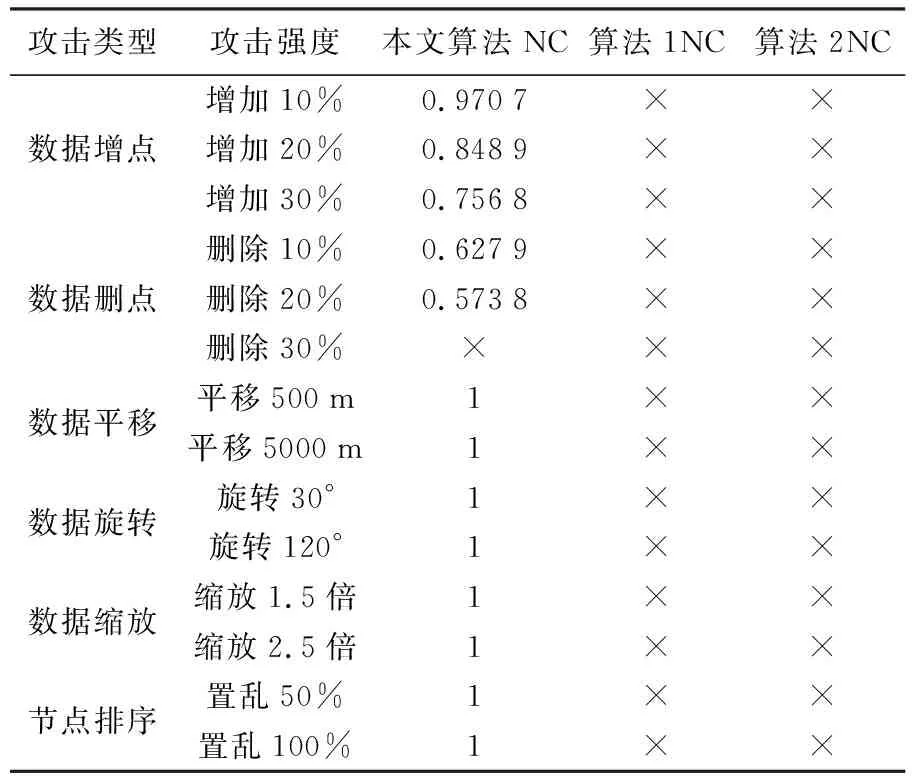
5 结 论

