二次CUBE滤波算法及在边坡乱石区测深数据处理中的应用

郑永新，张红梅，赵建虎

1. 武汉大学测绘学院，湖北 武汉 430079； 2. 武汉大学海洋研究院，湖北 武汉 430079； 3. 武汉大电气与自动化学院，湖北 武汉 430072

多波束测深系统(multibeam bathymetric system,MBS)因具有高密度、全覆盖测深特点[1-2]，在港口、航道等工程中有着广泛的应用。实际应用中，特别在海岸防波堤抛石工程中需要边施工边测量，对抛石间较大缝隙进行填补，这就需要比较准确和清晰的水下地形信息。然而，施工区域水下地形测量受悬浮物、石块遮挡、系统噪声和测量船噪声等影响，MBS获取的测深点云存在大量粗差，严重影响了测深数据对海底测量对象的准确描述，不能给予抛石施工准确的指导信息，必须给予有效滤除。据此，国内外学者开展了大量研究。目前，常见滤波方法主要有COP法[1]、Ware法[1]、Knight&Wells法[1]、Eag(RDANH)法[3]、趋势面法[1,4-5]、抗差估计法[6-7]、Bayes估计[8]、中值滤波[9]、均值滤波、局部方差检测和小波分析相结合的滤波方法[10]以及选权迭代加权平均[11]等方法。上述方法对于海量MBS点云数据处理存在速度慢，无法满足边施工边测量，近实时获取水下地形的需求，且普适性不高，乱石区等复杂海床测深数据滤波性能欠佳等不足，导致无法准确获取水下地形信息，无法正确指导抛石施工。在文献[12]提出MBS测深点的水平和垂直不确定度理论计算方法的基础上，文献[13—15]提出了CUBE滤波方法。由于该方法具有滤波高效、可靠、抗差、稳定等特点[16-19]，目前在CARIS和HYPACK等国际商用MBS测深数据处理软件中广泛使用[20]。当测深点在格网节点周围均匀分布，存在少量粗差时，CUBE算法可准确估计格网节点水深值。然而，在乱石区，现有CUBE算法会遇到如下问题：其一，MBS测量会因乱石遮挡产生测量盲区，导致盲区测深数据空白，波束可达区密集，测深数据分布(特别是在边坡乱石区)不均匀性问题突出，导致现有CUBE算法对边坡乱石区测深数据处理时估计节点的深度不准确；其二，现有CUBE算法仅开展深度估计，未顾及平面位置估计，乱石区的上述数据特征会引起估计的水深点位置不准确，从而引起地形特征混乱；其三，边坡乱石区地形变化复杂，波束在乱石间会产生多次回波后到达换能器，或因环境复杂，水中存在大量遮挡物时导致测深数据中存在大量粗差，基于现有CUBE算法的最优水深估值选择原则[13]将很难得到准确的水深，还需要借助手工编辑剔除粗差，也因此显著降低了数据滤波的效率，严重影响施工的进度。

为此，针对CUBE算法不足，在深入研究的基础上，提出了顾及平面位置估计和开展二次CUBE估计的滤波算法，以期解决上述问题，实现MBS测深数据对乱石区地形的真实反映。

1 CUBE算法原理及其不足

1.1 CUBE算法

CUBE是基于规则格网估计各格网节点最优水深的滤波方法，主要包括如下3个部分。

1.1.1 测深点深度不确定度传递

在根据水深确定格网节点搜索范围内，将测点水平和垂直不确定度σH,j、σV,j传递到待估格网点上[13]

(1)

式中，δij为测深点到待估格网点的平面距离；SH为水平不确定度的影响因子，默认为1.96；α为地形起伏影响因子，默认为2；Δmin为格网大小。

1.1.2 多重估计

以Kalman滤波方法建立估计方程[13]，式(2)和式(3)分别给出了状态方程与观测方程

z[n+1]=z[n]+w[n]w[n]～N(0,W[n])

(2)

(3)

式中，w[n]、v[n]为系统噪声和观测噪声，均服从正态分布。由于模型是为了获取格网节点的唯一水深，因此有W[n]=0 m2(文献[13])。

式(4)—式(9)给出了滤波估计过程[13]

(4)

(5)

(6)

(7)

(8)

(9)

定义图1(b)中σf为预测误差，图1(c)中d1和d2分别为输入水深值与估值1、估值2差值，则CUBE算法多重估计更新过程为：

(1) 初始化一个估值后或者只存在一个估值时，进行如图1(a)或图1(b)所示的过程。

(2) 存在多个估值时(如图1(c))选择与输入水深值差异最小估值，重复图1(a)或1(b)。

(3) 重复步骤(1)和(2)，对所有数据格网节点进行水深估计。

图1 CUBE多重估计更新Fig.1 Multiple estimation and update in CUBE filtering

1.1.3 最优水深估值选择原则[13]

原则1：选取估值纳入点数最多的一个估值作为最优估值。

原则2：在待估格网点周围一定范围内，寻找单个估计值的格网点水深为参考水深，寻找待估格网节点估值中与该参考水深最接近的估值作为最优估值。

原则3：综合原则1和2。

1.2 边坡乱石区CUBE算法的不足

(1) 忽略了边坡乱石区测深点的分布特点。

边坡乱石区MBS测量时，因大坡度地形、石块(图2(c))遮挡，导致大量测量盲区(图2(a))，测深点在垂直方向上间断分布(图2(a)、(c))。现有CUBE算法基于测点均匀分布(图2(b))和多重估计原理开展估值图2(c)中的测点分布不均匀问题会导致对节点Node的估计产生两个水深估值A和B。无论是选择A估值还是B估值，最终会赋值给Node作为该节点的估值，进而造成节点平面位置和水深估值不准，引起地形特征错位甚至错误。

(2) 无法消除大量粗差影响。

传统CUBE滤波给出了3个水深估值优选原则，其优缺点如下：

原则1：简单，易于实施，当地形平缓和测深数据中存在少量粗差时，可有效剔除粗差，但当粗差较多且集中分布时，易获得错误水深估值。

原则2：当地形平缓、粗差较少或者离散分布时，可有效消除粗差，具有抗差性，但当地形复杂、数据质量较差时，多重估计后将有大量的格网节点出现多个估值情况，此时很难找到只有单个估值情况。如取舍不当，会导致待估格网点水深错误。

原则3：情况同原则1和2。

实际数据处理时，如图3(a)中红色区域为边坡乱石区，采用CUBE算法对该区水深数据进行滤波，每个格网节点将获取多个估值，因此原则2、3无法实施，只能采用原则1选择最终估值。然而，针对图3(b)矩形区测深数据中存在大量粗差，借助原则1获取的估值如图3(c)，可看出传统CUBE并未完全消除粗差的影响。

2 顾及数据特征的二次CUBE滤波算法

在边坡乱石区，为解决因原始波束数据中存在大量粗差产生的由传统CUBE滤波带来的节点估值不准问题(如图3(c)所示)，提出一种快速二次CUBE滤波方法。

2.1 顾及位置估计的一次CUBE滤波

针对1.2节中问题(1)，本文提出在传统CUBE算法的基础上，在进行水深估计的同时对水深估值的平面位置估计。平面位置估计与水深估计类似，将水深值z用平面坐标(x、y)代替，用每个波束的水平不确定度代替水深不确定度。采用类似式(5)、式(7)和式(8)的形式，则有

(10)

(11)

(12)

在传统CUBE滤波方法的基础上，增加位置估计，对原始的测深数据开展一次滤波。顾及平面估计的一次CUBE滤波所得散点(图4中所示的三角网节点)不再是每个格网节点。

2.2 二次CUBE滤波

提取一次CUBE滤波所得散点水深值、不确定度及对应的每个点上多重估计水深。如图4所示，图中中心点(xm,yn)为待检测点，以该点为中心，直径为a的圆范围内测深点对该点估值进行检测，a=2x×Δmin(x≥1,x∈N)。节点上估值的垂直不确定度为

(13)

式中，k表示节点(xi,yj)的第k个估计值；nk表示该估值的吸收的测深点数；σv,j表示该估值纳入的第j个测深点的垂直不确定度。

将周围点(xi,yj)的不确定度σ(i,j)传递到待估点(xm,yn)上。本文顾及平面位置影响和乱石区地形梯度变化显著特点，给出传递模型如下

(14)

当水深小于50 m，波束大小为0.5°×1°，仪器量程分辨率为1.25 cm，条带覆盖角120°，假定节点不确定度σ(i,j)为0.15 m，则根据式(14)，表1列出了当周围点距待估点距离为1Δmin时不同μ将对应不同大小的σi,j值。由表1可知，假设相邻节点水深值差异为0.5 m，为容许该水深差，σi,j应该大于0.5 m，此时μ应大于3，取值4。μ不能过大，否则可能会导致粗差滤除失败。μ值参数需根据当前测量水深的不确定度和地形起伏来综合确定。

σ(i,j)/mμσi,j/m0.1530.4740.1540.6180.1550.765

然后，采用多重估计对水深点值与周围一定范围内的水深值进行一致性检测(如图1)。若发现该水深值带有粗差，利用周围水深值采用多重估计和最优参考水深选择方法获取最优水深参考值dr。dr的选取过程如下：

(1) 将一次CUBE滤波获得的待估点水深作为初始估值d0，利用直径为a区域内的所有点的平面和水深一次估值结果，对待估点进行多重估计，并统计每个估值纳入的点数ξi。

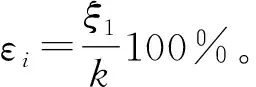
(3) 根据各估值的百分比εi，寻找最大的εmax。若εmax≥ε′，则εmax对应的估值即最优水深参考值dr；否则，表明未能找到任何可靠的水深参考值，删除或标记待检测节点为不可靠点。

最后，给出如下方法，开展二次水深估计:

(1) 从一次CUBE滤波多重估计结果中获取与dr差异最小的水深估值d(m,n,index)

(15)

式中，index为对应索引数;count为待估点上的一次CUBE滤波获取的多重估值个数。

(2) 然后计算地形梯度变化量ddiff

(16)

(3) 顾及地形梯度ddiff，基于式(17)的原则确定最终水深估值df

(17)

式中，df为最终水深优选估值。

获取可靠水深值的同时，更新该点平面位置。对所有一次CUBE滤波后点进行上述二次滤波处理，最终完成乱石区测深数据的滤波。

3 阈值参数的确定

3.1 搜索范围直径a的确定

如图4所示，极端情况下，假设黑色点及中心点全为粗差点，随着直径a增大，区域粗差率降低。理论上，粗差率越低，越易获得无粗差影响的参考值，但对于复杂地形，a过大，最终获得的参考值与待估点的地形相关性将大大降低，使得待估点水深估值优选结果不可靠。所以参数a取值时既要考虑粗差率，又要顾及地形起伏。

当直径a取2、4、6倍Δmin，图4中圆形区包含的粗差格网点数占该区域总点数(包含区域边缘点)的百分比分别为100%、42.9%和20.5%。粗差率一定的情况下，地形变化较大，a应取较小值，这样获取参考值时纳入的节点与待估点越靠近，参考值与待估点水深值在地形上相关性更大，最终优选得到的水深值越可靠。粗差率通常是未知的，但与地形坡度、水深和测量设备等相关。试验区大量试验表明，水深小于50 m，地形坡度大于30°，Δmin=0.5 m，粗差大量聚集时，a取6Δmin较为合适；地形坡度小于30°，a取6～8倍Δmin较为合适。

3.2 有效点数阈值η给定

η是确保以待估点为中心，直径为a范围内有足够多的有效水深值点数。如果有效点数太少，获取的参考水深可靠性将大大降低。地形边缘或数据稀疏地方，有效点数较少，这种点的可靠性较差(往往表现为破碎地形)，可以将其删除或者标记。有效点数取值可以根据直径为a的搜索区域的外接正方形包含的点数得到，即η=ceil[(a/Δmin+1)2/2]，其中ceil函数为向上取整。

3.3 阈值ε′的确定

阈值ε′用于判断待检测节点水深值和选择可靠的参考水深估值。如图4所示，若图中较大的黑色格网圆节点及中心点皆为异常点，由3.1节可得，当a=6Δmin时，粗差率为20.5%。如果ε′小于粗差率，可能将待估点水深值判断为可靠值，从而导致错误检测，因此，ε′必须大于粗差率，才能保证获得正确的检测结果。同时，为了获得可靠的水深参考值，阈值ε′不宜过大。因此，ε′应满足20.5%<ε′<50%。

4 试验及分析

为验证本文方法对乱石区MBS测深点滤波的有效性，试验采用以色列海岸防波堤抛石工程施工区测量数据。该数据采用Sonic2024多波束测量仪器[21]采集，表2为Sonic2024各项误差分量[13]。测区水深1～25 m，最大浪高小于0.25 m，海洋潮汐影响0.1 m左右。边坡抛石区石块大小不一，呈现不规则分布。根据施工要求，每次抛石后都要对水下抛石区域进行测量，准确掌握每次抛石情况，为下一次抛石提供指导。受乱石区多次反射波等影响，测量数据中存在大量粗差，如图5中椭圆形虚线区域所示。

以下采用3种数据处理方案开展试验，分析本文方法的性能。

方案1：采用Caris中传统CUBE算法滤波。基于CARIS软件(内置CUBE滤波)对测深数据处理，结果如图6(a)和图7(a)所示。方案1基于格网数据估值，估值结果仍存在大量粗差，错误地反映了边坡乱石区地形。

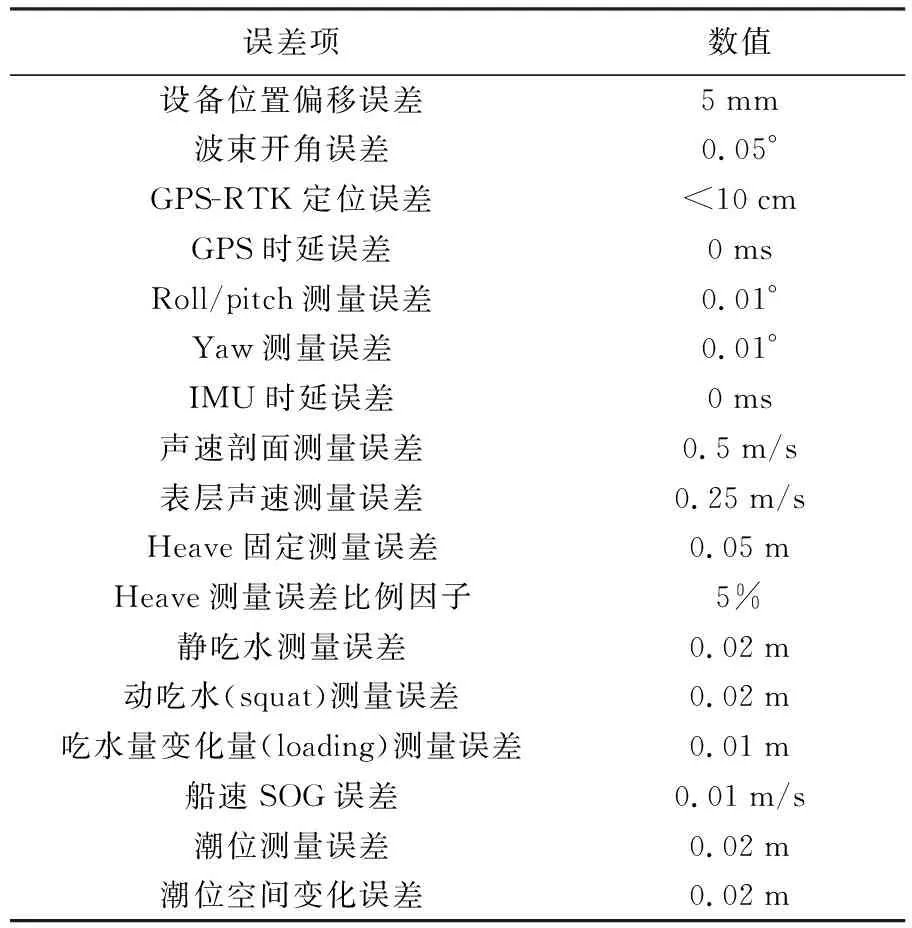
表2 Sonic2024各项误差分量

方案2：二次CUBE算法滤波。试验中Δmin=0.5 m、a=3 m、η=25、ε′=25%、μ=4。试验结果如图6(b)、(d)和图7(b)所示。因同时开展了水深和位置估计，因此估值结果不再是格网节点，而是一系列散点，采用三角网构建地形模型更为恰当(图6(d))。利用该方案检测出了大量的异常测深点如图7(d)所示(图7(a)、(b)、(c)均为(d)中红色矩形区域侧视图)，由图7(a)、(d)可知，检测出的异常点分布与实际吻合，最终滤波结果粗差剔除彻底。抽取图5中边坡乱石区矩形区域内(图5(b))的原始测深数据，采用方案1和方案2处理，滤波结果分别如图6(a)、(c)和(b)、(d)所示。可以看出：

(1) 方案2块石地形特征更加明显，石头间隙更加分明，粗差被彻底消除。

(2) 比较图6(c)、(d)，方案2得到的估计点在平坦地区几乎与方案1得到的格网节点分布一致，在复杂地形区则存在明显差异，但对乱石区地形描述更真实。

(3) 方案2顾及了乱石区测深数据特点，同时开展了位置和水深估计，并基于二次滤波消除了粗差影响，因此为测深点赋予了准确的三维估值，从而也实现了对地形的真实表达。

图2 边坡乱石区测深点分布及对估值的影响Fig.2 Effects of sounding point distribution on sounding estimationin slope riprap area

图3 乱石区传统CUBE滤波结果Fig.3 Traditional CUBE filtering results in underwater riprap area

图4 二次CUBE滤波Fig.4 Second CUBE filtering

方案3：CARIS手工编辑。方案3基于CARIS滤波后出现粗差时常采用的一种补救措施，因边坡乱石区地形复杂，有时难以判断准确的地形信息，需要有丰富的水深数据处理经验。如图7(c)所示，异常测深点被剔除，基本反映了实际地形变化，但过程非常耗时。以方案3结果为参考，方案1和方案2滤波获得的水深值与之比较，差值分布如图8所示，统计结果如表3所示。

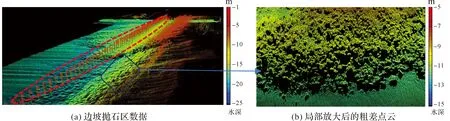
图5 边坡抛石区地形及大量粗差点云Fig.5 Slope riprap point cloud with a large number of gross errors

图6 方案1和方案2滤波地形及格网Fig.6 Filter terrain and grid obtained by solution 1 and solution 2

图7 大量粗差剔除Fig.7 Removing a lots of gross error

Tab.3 Statistics on the estimation error of water depth in slope riprap of different methods m

从图8和表3可知：

(1) 方案2偏差最小，且偏差分布符合正态分布。

(2) 方案1偏差均值较大，主要因其机理不足所致，也进一步表明了本文工作的必要性。

(3) 方案1中的问题未在方案2结果中出现(如图7(b)和图8(b)、(c))；方案2实现了自动处理，且将方案1的成果精度提高了近5倍，从而也验证了本文方法的有效性。

5 结 论

本文基于数据特征提出的二次CUBE滤波算法，给出了位置和水深的同步估计方法、顾及地形梯度的平面和水深不确定度传递模型、参考水深的多重估计和优选算法并顾及地形梯度的二次水深估计模型，解决了传统CUBE滤波算法在乱石区出现的水深估计不准确、地形特征模糊和粗差剔除能力不足等问题，实现了边坡乱石区水深的准确估计。试验表明，二次CUBE滤波算法实现了粗差的自动检测和测深点的准确估值；在乱石区，大大提高了传统CUBE算法水深估值的精度，形成的地形特征更加准确和明晰；在平坦海床，取得了与传统CUBE滤波算法近似相同的地形结果。相对传统CUBE滤波算法，二次CUBE算法的抗差性更强，数据处理效率更高。