距离门宽度对单光子激光测高卫星探测概率及测距精度的影响

李国元，黄佳鹏，唐新明，黄庚华，周世宏，赵严铭

1. 国家测绘地理信息局卫星测绘应用中心，北京 100048； 2. 中国科学院空间主动光电技术重点实验室，上海 200083； 3. 江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023； 4. 上海卫星工程研究所，上海 201109

卫星激光测高被列为对地观测系统核心的信息获取技术之一。我国于2016年5月发射了搭载国内首台对地观测激光测高仪的资源三号02星[1]，而美国在2003年就成功发射了冰、云和陆地高程卫星ICESat(ice,cloud and land elevation satellite)，搭载了线性体制的地球科学激光测高系统GLAS(geo-sciences laser altimeter system)，在极地冰盖监测、全球高程控制点获取、森林生物量估算等方面得到了较好的应用[2-3]。ICESat的后续星ICESat-2已于2018年9月成功发射。ICESat-2可以量化两极地区冰川与海平面变化、评估海冰厚度、测量植被冠层高度、估计生物量变化等[4]。与ICESat搭载的线性探测器记录时间相关的回波波形相比，ICESat-2采用的是基于盖革模式的单光子激光探测技术，能够进行多波束、微脉冲、高重频的密集高程测量，单光子探测将是下一代激光测高卫星的发展方向[5]。该技术的核心要素之一就是距离门宽度的有效确定[6-9]。

国内外围绕单光子探测的距离门宽度开展了较多的研究，文献[10]提及一种根据地形数据库设置距离门宽度的算法，可以根据同一地区的数字地形图(digital relief map,DRM)、数字高程模型(digital elevation model,DEM)、地表参考标记(surface reference mask,SRM)确定需要测量目标的实际情况，进而调整距离门宽度获取更精准的测量结果。文献[11]通过测距精度与回波脉冲强度及宽度的相互关系式，通过试验证明回波激光脉冲强度越高，脉冲宽度越窄，所获得的距离精度越高。文献[12]根据激光外差探测原理和光子计数探测的统计理论，建立了系统测距精度模型，研究了激光回波强度、脉宽等6个因素对测距精度的影响。文献[13]针对常见的高斯回波波形，基于激光雷达方程、单光子探测器统计特性，建立了单光子回波探测概率模型，然后基于该模型进一步推导了测距误差的量化关系式，但是并未考虑距离门和噪声情况，而且对于部分公式选择了简化处理。文献[14]给出了盖革模式下APD阵列激光雷达在广域地形测量的最新研究成果。文献[15]通过分析了APD阵列增益对系统信噪比和探测概率的影响，证明选取的APD阵列增益合适时，系统的信噪比和探测概率可以达到最大值。文献[16]通过试验证明提高回波光子数、探测占空比有助于增加APD阵列探测信噪比。

距离门宽度对于单光子激光测距误差影响很大，但目前还没有针对距离门宽度与探测概率及测距误差大小的关系进行定量化描述的研究。本文针对这一问题进行理论分析，并采用蒙特卡洛模拟方法进行仿真验证。

1 理论分析

1.1 单光子测高卫星距离门测距原理

激光测高卫星通过测量卫星发射的激光脉冲到地面目标的往返时间来确定目标距离。单光子激光探测器每探测到一个或少量返回光子，即输出一个脉冲信号，以此作为本次测量计时停止的标志[17]。卫星上搭载的激光探测器发出的激光脉冲会往返经过大气层，为减少云雾、太阳背景噪声等对于测量精度的影响，激光接收探测器内需要采用距离门(range gate)技术，在特定距离内的光子才被记录，距离门外的返回光子不予记录，根据不同区域的地形起伏需要设定不同宽度的距离门[11]。对于采用距离门技术的单光子激光测高系统，其工作时序如图1所示。通过分析单光子激光测距的流程，可以发现距离门对如何有效提高测距精度具有重要意义。在距离门外，激光探测器不响应光子信号，仅在感兴趣的探测距离内，打开距离门开始光子探测，当距离门宽度合适时能大幅降低大气或其他因素产生的背景辐射和后向散射噪声的影响。

1.2 距离门宽度对探测概率的影响

假设距离门宽度为gw，激光脉冲宽度为pw，若时间分辨率为τbin，则距离门内共有q=gw/τbin个探测时隙。回波脉宽大于距离门的分辨时间时，脉宽包含的时隙数为r=pw/τbin。在探测间隔[t1,t2]内不发生探测的概率为P(0)=e-k，探测到一个或多于一个初始光子的概率为

P(k>0)=1-e-k

(1)

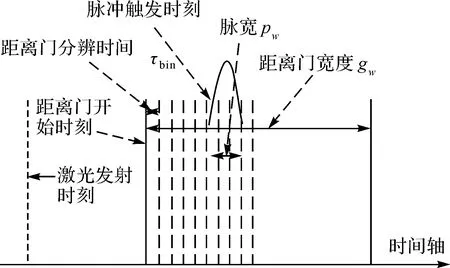
图1 激光探测器距离门工作时序图Fig.1 The working sequence diagram of laser detector range gate

式中，k为发生的事件次数。由于盖革模式的探测器在距离门内只产生一次探测，故其在第j个时隙产生探测的概率是条件概率分布，为前(j-1)个时隙内没有产生探测的概率与在第j个时隙内发生探测的概率的乘积

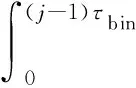
(2)

因此，回波激光脉冲的目标探测概率为

(3)

式中，r是N(t)所占据的分辨时间的个数。回波激光脉冲的虚警率为

Pfalse=1-PD-exp(-N-nbgw)

(4)

式中，N为有效光子数；nb为噪声数；gw为距离门宽度[18]。

1.3 距离门宽度对测距精度的影响

单光子探测器接收到的有效光子个数随时间变化函数为

(5)

(6)

式中，nb为噪声光子数，则在距离门内探测到信号的条件概率为

(7)

式中，P(t)为条件概率，即落在距离门内且探测到信号的概率；1-exp(-N(gw))为落在距离门内的概率；P(k>0)为探测到信号的概率；η为信号探测效率。

概率密度函数如式(8)所示

(8)

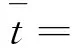
(9)

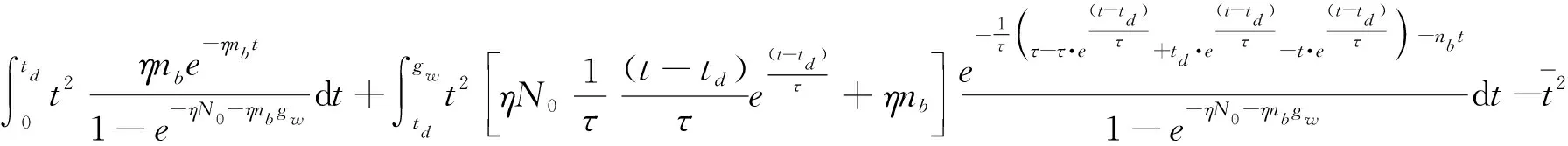
(10)

式中，nb为背景噪声；gw为距离门宽度。

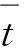
(11)

式中，td为激光回波位于距离门的位置；c为光速，本文取光速c=3×108m/s。

2 试验验证

2.1 理论公式验证

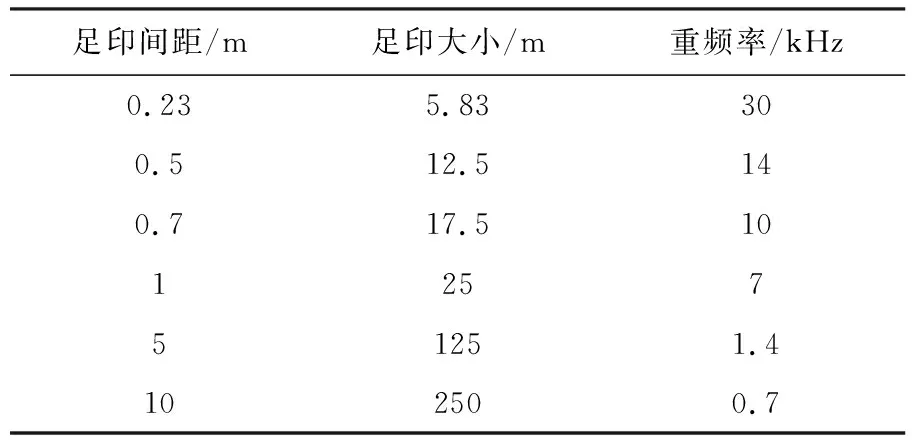
根据上节中的理论分析，采用式(3)、式(4)统计不同距离门宽度下的理论探测概率和虚警率，如图2所示。图2中黑色线段为不同距离门宽度对应的探测概率，红色线段为虚警概率。图2(a)中带三角号的线段为距离门宽度为200 ns，带星号的线段距离门宽度为300 ns，带圆圈线段距离门宽度为400 ns。图2(b)中带三角号的线段距离门宽度为20 000 ns，带星号的线段距离门宽度为30 000 ns，带圆圈线段距离门宽度为40 000 ns。其余参数分别为背景噪声nb为50 kHz，时间分辨率为τbin=0.5 ns，回波位置td始终保持在距离门中间。

图2在黑色线段代表的探测概率出现重合部分，在红线虚警概率部分也有部分重合区域，是因为选择的关于探测概率的公式与距离门关系较小，虚警概率与距离门有较大关系，但是当距离门达到一定宽度时，虚警率变化也不大。

为了较为直观地分析距离门对于测距精度的影响，选择激光脉宽pw为1 ns在距离门宽度gw分别为100、200、300、400、500、1000、2000、3000、4000、5000、10 000、20 000、30 000、40 000和50 000 ns时，根据式(11)、式(12)计算测距误差均值和标准差的理论结果，其余参数分别为背景噪声nb为50 kHz，探测效率η为50%，有效光子个数为20，回波位置td始终保持在距离门中间。图3(a)、(b)中表示有效光子个数为20时，100～500 ns以及1000～5000 ns不同距离门宽度下测距误差均值及误差标准差的大小，其中带三角形的直线为误差均值，带星号的直线为误差标准差。

通过比较不同宽度距离门精度指标，可以看出，图3(a)、(b)图变化趋势相同，但是图3(b)变化范围更大。随距离门宽度增大，误差均值和误差标准差都逐步增大，误差标准差增大程度明显，表明随距离门宽度变大，测量获得的光子中有较多的噪声。

2.2 模拟数据验证

本节基于蒙特卡洛模拟方法对距离门宽度影响下的探测概率及测距精度进行仿真分析。蒙特卡洛模拟方法也叫统计模拟方法，18世纪出现的著名的“投针试验”被认为是该方法的起源，之后直到20世纪由John von Neumann和Stanislaw Ulam合作将这种方法命名为“蒙特卡洛方法”。该方法主要通过对所研究系统的状态进行随机抽样，进而对获取的样本结果进行计算统计，最终使用随机状态的发生频率来估算概率，并将其作为问题的解[20]。为验证第1节中距离门宽度与探测概率以及测距精度理论分析的准确性，采用蒙特卡洛模拟方法，随机选择100次有效光子探测事件，统计该距离门宽度下的相应探测概率及虚警概率，然后改变距离门宽度大小，重复进行新的模拟试验。除距离门宽度发生变化外，其他参数的设置为：背景噪声nb=50 kHz，时间分辨率为τbin=0.5 ns，回波位置td始终保持在距离门中间。不同距离门宽度下，使用蒙特卡洛方法进行仿真试验得到图4，红色为虚警概率，黑色为探测概率。由理论公式计算和模拟仿真数据得出距离门宽度与探测概率、虚警概率对比结果如表1所示。

表1不同距离门宽度影响探测概率和虚警概率的理论值与模拟仿真结果对比

Tab.1Comparisonbetweentheoreticalvaluesandsimulationresultsofdetectionprobabilityandfalsealarmprobabilityinfluencedbydifferentrangegatewidths

距离门宽度/ns探测概率/(%)虚警概率/(%)理论计算值模拟仿真结果理论计算值模拟仿真结果10097.4397.042.532.7120097.4396.912.532.7730097.4396.972.542.7840097.4397.112.542.7150097.4397.122.542.72100097.4397.022.552.81400097.4396.912.573.031000097.4397.042.572.954000097.4397.062.572.93

取不同的距离门宽度，采用如上述同样的蒙特卡洛模拟方法，对测距误差均值和标准差进行统计，理论计算与模拟仿真对比的统计结果见表2。

表2不同距离门宽度影响测距误差均值和标准偏差的理论值与模拟仿真结果对比

Tab.2Comparisonbetweentheoreticalvaluesandsimulationresultsofaverageandstandarddeviationrangingerrorinfluencedbydifferentrangegatewidths

距离门宽度/ns测距误差均值/m测距误差标准差/m理论计算值模拟仿真结果理论计算值模拟仿真结果1000.0160.0170.1540.1542000.0020.0030.4340.433300-0.021-0.0200.7950.796400-0.054-0.05351.2231.2231000-0.446-0.4454.8134.8144000-7.356-7.35537.78137.78310000-44.962-44.961143.885143.89040000-639.167639.163959.848959.876

考虑到距离门超过400 ns时，测距误差均值和标准差均大幅增大，取距离门宽度分别为400、1000、4000、10 000和40 000 ns，采用蒙特卡洛模拟1000次，对测距误差x按照|x|<0.1 m、0.1 m<|x|<0.3 m、0.3 m<|x|<0.5 m、0.5 m<|x|<0.7 m、0.7 m<|x|<0.9 m以及0.9 m<|x|等6种情况统计测距误差所占百分比，结果如图5所示。

2.3 光斑大小与重频关系

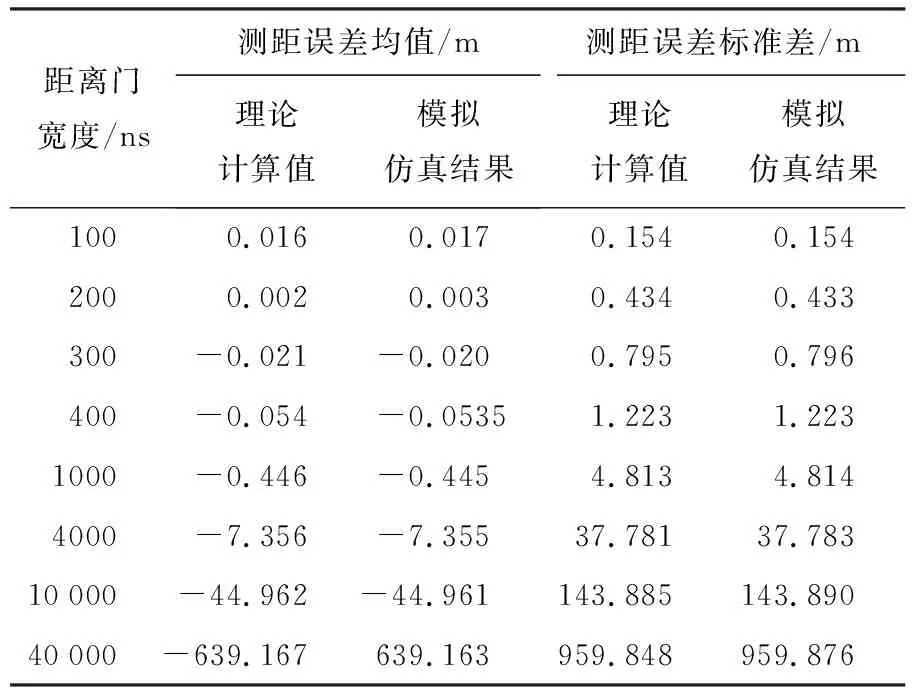
不同于ICESat-1的线性探测机制，ICESat-2搭载的单光子激光器具有高重频特性，发射频率高达10 kHz，相邻足印间距为0.7 m，但ICESat-2的激光光斑地面足印大小从原来设计的10 m调整为17.5 m，导致激光测高卫星对于相同点重复观测次数可以达到25次[21]。由于星载单光子激光器探测灵敏度高，受太阳光等背景噪声影响大，为保证测量的密度和精度，在兼顾光斑大小的情况下，尽可能提高重频次数是提高其测距精度的重要方式之一。笔者认为重复观测25次是在当前单光子技术条件限制下，NASA(National Aeronautics and Space Administration)官方针对ICESat-2选择的最优重复观测次数。根据ICESat-2的卫星轨道高度及卫星运行速度，如果要保持同一区域25次重复观测，重频率与激光足印大小及间距的定量化对应结果如表3所示。如果要求地面足印较小，则重复频率需大幅提高，对激光器的要求也会更苛刻，NASA最终选择了维持10 kHz重频率、扩大足印直径到17.5 m，但两者之间如何配比才能实现硬件复杂度与测量精度的最佳组合还有待继续探讨分析。

表3保证重复观测次数为25次时足印间距和大小以及重频率对应关系

Tab.3Thecorrespondencebetweenthespacingandsizeofthefootprintsandtherepetitionfrequencywith25timesofrepeatedobservation

足印间距/m足印大小/m重频率/kHz0.235.83300.512.5140.717.510125751251.4102500.7

3 讨论与分析

从图2可以看出，不同距离门对于探测概率的影响并不大，而对虚警概率有一定影响，但距离门较小时虚警概率也很小。其中，当距离门宽度为400 ns，有效光子数达到8个时探测概率为97.43%，虚警概率为2.54%。距离门为4000 ns，有效光子数达到8个时探测概率为97.43%，虚警概率为2.57%。距离门为40 000 ns，有效光子数达到8个时探测概率为97.43%，虚警概率为2.57%。结合图4及表1的对比统计结果可以看出，蒙特卡洛仿真的数据图形与理论推导数据图形变化趋势类似，且数值基本一致，进一步说明了试验中关于距离门对探测概率及虚警率分析的准确性。

从图3可以看出，在有效光子个数为20时，距离门宽度为100 ns的误差均值为0.02 m，误差标准差为0.15 m。但是，距离门为100～500 ns时对应探测景深仅为15～75 m，这不符合激光测高卫星要求的探测景深。文献[10]提出探测景深保持在6 km，对应距离门宽度为40 000 ns，但是距离门为40 000 ns情况下，计算所产生的误差均值和误差标准差与激光测高卫星精度要求相差很大，误差标准偏差甚至超过了900 m，这在表2中得到了进一步验证。

图2 不同距离门宽度下的单光子激光探测概率及虚警率Fig.2 The detection probability and false alarm rate of the single photon laser under different range gate widths

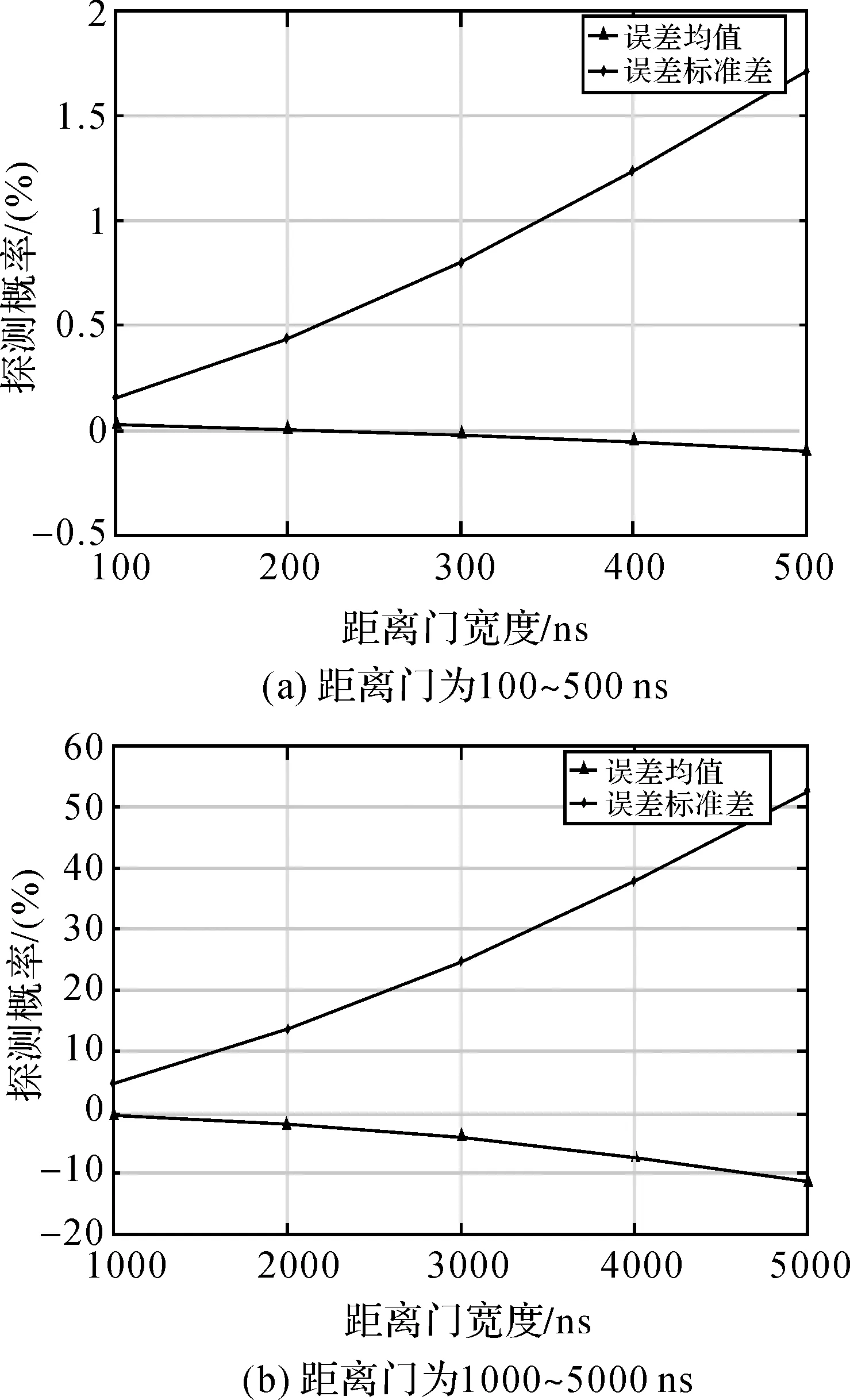
图3 测距精度随距离门宽度变化情况Fig.3 The relationship between the ranging error and range gate width

图5 不同距离门测距误差统计结果Fig.5 The error statistical result of different range gate widths

虽然距离门为40 000 ns时，总的测距误差很大，但图5的误差分布统计图表明，距离门宽度为400 ns时，误差主要集中于|x|<0.1 m，有个别点出现在|x|>0.9 m的范围。距离门宽度为4000 ns时，误差也相对集中于|x|<0.1 m，但是其他误差占比变大。距离门为40 000 ns时，在|x|<0.1 m占比明显减小，在其他误差范围误差占比出现明显增多。证明距离门增大后，背景噪声触发增多是导致误差均值和误差标准偏差变大的主要原因，需要通过数据后处理的精细化滤波算法提取误差较小的有效光子，以保证最终的测距精度。

笔者对于我国单光子激光器发展进行了调研，通过调研发现业务化应用的激光器重频率达到10 kHz已经是我国激光载荷的极限，若降低重频率且保证一定重复观测，则增大光斑是必然选择，而大光斑包含较多地物信息，高程测量精度的可靠性会有所降低。如果要保证重复观测25次，且保证激光足印点的密度和精度，除ICESat-2设计的足印大小17.5 m、重频率10 kHz的指标外，足印大小25 m、重频率7 kHz也是一种可选的方案。

4 总结与展望

本文分析了距离门宽度对单光子激光测高卫星探测概率和测距精度的影响，并采用蒙特卡洛模拟数据进行了验证，可得出以下结论：

(1) 距离门宽度对于单光子激光探测概率影响不大，对于虚警概率具有较大影响，当距离门宽度很大时，虚警率也相应提高。这也从另一个角度证明当距离门较大时，总的测距精度会急剧下降的原因。

(2) 为满足激光测高卫星的需求，当距离门宽度开得较大时，测距精度会急剧下降。当距离门宽度设为100 ns时，测距误差标准差为0.15 m，距离门大于400 ns后测距标准差会超过1.0 m，但其中仍有很大部分光子的测量误差在0.15 m范围内，此时需要借助后处理算法进行精细化去噪滤波提取有效信号。

(3) 目前我国实验室的单光子激光器载荷研制取得了一定进展。若以我国自主单光子激光器作为主载荷完成高精度测量，设计好激光重频率与足印大小及间距的对应关系非常重要。除ICESat-2设计的足印大小17.5 m、重频率10 kHz的指标外，足印大小25 m、重频率7 kHz也是一种可选的方案，希望可以为后续单光子卫星的参数设计提供参考。

近几年来，我国在卫星激光测高领域得到较快发展，搭载了国内首台对地观测试验性激光测高仪的资源三号02星已于2016年成功发射，装备了线性体制激光测高仪的国产高分七号、陆地生态系统碳监测等卫星也将陆续发射升空[2]。而美国的单光子激光测高卫星ICESat-2于2018年9月成功发射，相比而言，国内在单光子激光测高卫星的布局略显落后，迫切需要开展相关的论证及预研工作。ICESat-2卫星在距离门宽度设定方面进行了很大的创新，包括提高星上全球参考地形数据的精度、改进后处理算法等，这些都值得借鉴和参考。