类椭球体放矿理论实际散体速度方程和密度方程的构建

李荣福 郭进平 刘少青

（西安建筑科技大学材料与矿资学院，陕西西安710055）

类椭球体放矿理论是李荣福教授在实验观察、回归分析和理论研究的基础上创立的［1］。类椭球体放矿理论创立时，实际散体速度方程和密度方程都是各自独立给出的，虽然方程都通过了理论检验，但论证欠充分。本研究主要讨论实际散体速度方程和密度方程的构建过程，进一步证明类椭球体放矿理论创立时给出的实际散体速度方程和密度方程有坚实的实验基础和充分的理论依据，说明类椭球体放矿理论体系是严密的，自身闭合的。

1 密度方程的构建

1.1 密度经验公式

密度经验公式是根据实验结果建立的符合实验规律的经验公式，大量的放矿实验可以得到以下结果［3］：①理论放出口（Q=0）放出体的密度为放出密度 ρo，松动体Qs表面（Q=Qs）的密度为初始密度ρa；②移动体表面各质点介质密度相等，为等密度面，其密度为 ρ，且有0≤Q≤Qs，ρo≤ρ≤ρa；③松动体体积Qs是放出体体积Qf的C倍，即Qs=CQf，C是一个与放出条件和散体性质相关的实验常数，称为松动范围系数；④理想散体的松动范围与Qf值无关，且Qs→∞，并有松动范围内各处密度均为初始密度 ρa，也是放出密度 ρo，即 ρ=ρo=ρa。

由以上实验结果可知，经验公式应满足以下条件：Q=0时，ρ=ρo；Q=Qs时，ρ=ρa；0＜Q＜Qs时，ρo＜ρ＜ρa；Qs→∞ 时，ρ=ρo，Q 表面各处密度都相等。经验公式还应具有良好的可调性。

类椭球体放矿理论创建过程中，提出的符合实验结果的密度经验公式如下：

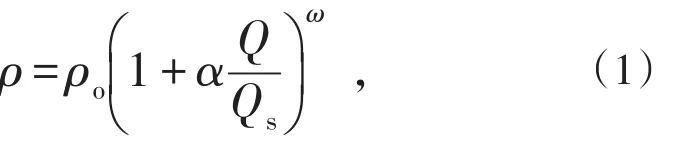
式中，α，ω均为与密度及其变化相关的实验常数。

1.2 类椭球体放矿理论的密度方程

类椭球体放矿理论的密度方程应满足质量守恒定律的理论要求。根据质量守恒定律得到松动体质量平衡方程式：

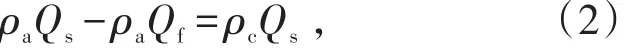
式中，Qs、Qf分别为松动体体积和放出体体积；ρa为散体初始密度；ρc为松动体Qs中散体的平均密度。

根据密度经验式（1），得到松动体Qs中散体的平均密度 ρc值为：

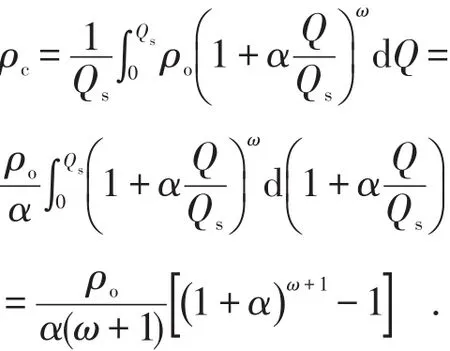
当Q=Qs时，ρ=ρa，由密度经验公式可知，初始密度 ρa值为：

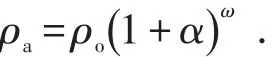
由松动体质量平衡方程式（2）得：

代入 Qs=CQf和 ρa、ρc值得：

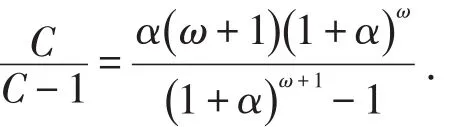
由于上式不存在变量，成立的必要条件是C=(1 +α )ω+1=α(ω +1)(1 +α)ω，故存在 ω=。也就是说密度经验公式只有ω=时才能满足质量守恒定律的理论要求。因此，符合实验结果又满足理论要求的密度方程为：

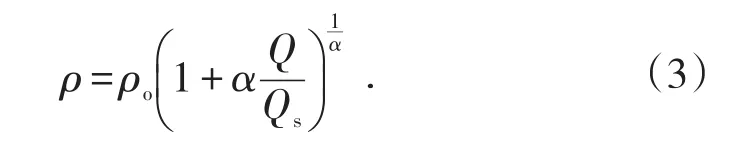
式（3）表达的密度方程正是类椭球体放矿理论创立时给出的密度方程。它是一个由经验公式上升为理论公式的密度方程。由密度方程式（3）的构建过程可知，该密度方程具有坚实的实验基础和充分的理论依据。

2 实际散体速度方程的理论表达式

类椭球体放矿理论创立时，在实际散体速度方程的构建中，认为实际散体速度是理想散体速度与速度阻滞系数之积，现论证其理论依据。

2.1 理论表达式的基础方程［2，4-5］

类椭球体放矿理论根据理想散体的移动过渡方程建立了理想散体速度方程式（4）和式（5）。

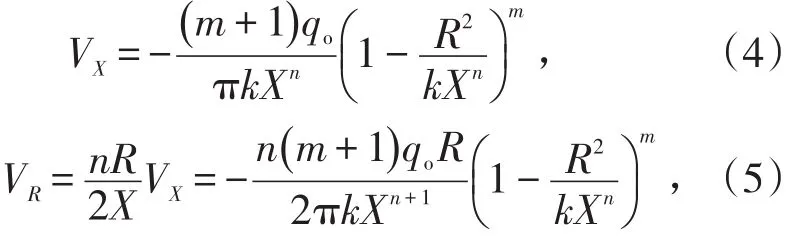
式中，VX、VR分别为理想散体垂直下移速度和径向速度；X、R分别为圆柱面坐标系的垂直坐标和径向坐标；qo为单位时间放出体积；n、m、k均为与放出条件和散体性质相关的实验常数。

由类椭球体放矿理论可知，移动体体积方程为式（6），放出体体积方程为式（7），移动迹线方程为式（8）：

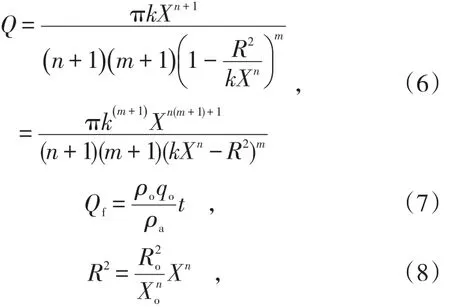
式中，Q、Qf分别为移动体和放出体体积；Xo、Ro分别为颗粒点移动前的初始垂直坐标和径向坐标；ρa、ρo分别为散体初始密度和放出密度；t为放出时间。

2.2 实际散体速度方程的理论表达式建立

已知Q是X和R的函数，根据微分运算法则有：

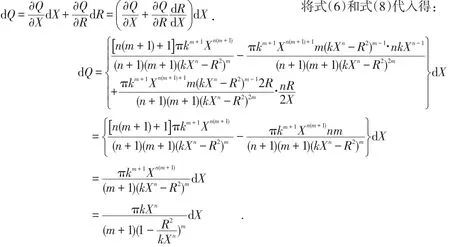
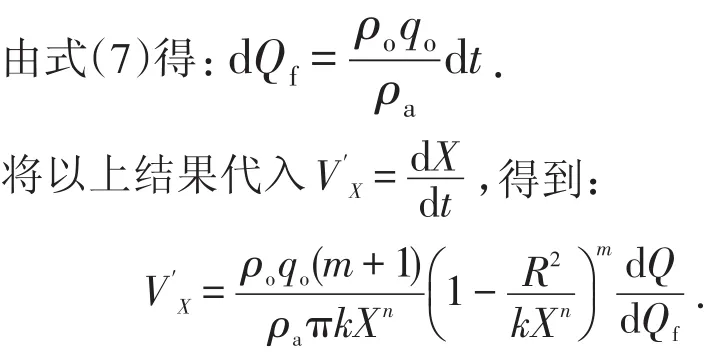
根据式（4）可进一步得到：

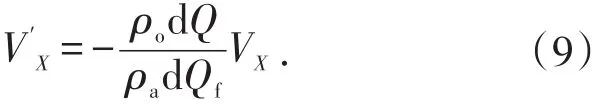
式（9）为实际散体速度方程的理论表达式，它表明实际散体速度是理想散体速度与

设

其中，β称为速度阻滞系数，式（10）是速度阻滞系数的理论表达式。

实际散体速度方程的理论表达式（9）则可转换成速度阻滞系数β的表达形式：

由式（10）可知，速度阻滞系数 β与散体场密度及其变化相关，它表明由于实际散体密度场的不均匀性和不定常性的性质，使得散体移动场中的散体颗粒存在投入运动滞后和速度减慢的阻滞现象。实验研究表明，实际散体放出时产生二次松散现象，造成散体移动场中各处密度都发生变化，使得散体颗粒运动滞后和受阻而减速。实际散体在放出口处（Q=0），不再产生二次松散，也无速度阻滞现象（β=1）。松动体表面各处（Q=Qs），受速度阻滞最大，速度变为零（β=0）。在移动场中随移动体Q增大则 β值减小，且有0＜Q＜Qs，1＞ β＞0。理想散体由于不产生二次松散，没有速度阻滞现象（β=1）。

式（11）表明实际散体速度是理想散体速度与速度阻滞系数之积。式（11）正是类椭球体放矿理论创立时给出的实际散体速度的表达式。

由以上论证可知，类椭球体放矿理论创立时提出的速度阻滞系数概念，并认为实际散体速度是理想散体速度与速度阻滞系数之积的观点是正确的且有理论基础的。

3 类椭球体放矿理论实际散体速度方程

类椭球体放矿理论创立时，其实际散体速度方程中给出的速度阻滞系数理论依据，且与速度阻滞系数 β的理论表达式（10）不同，下面对此进一步论证。

3.1 类椭球体放矿理论的速度阻滞系数

由上节得到式（10）所示的速度阻滞系数的理论表达式，现根据类椭球体放矿理论的密度方程和移动体质量平衡方程来求算速度阻滞系数。

当放出量为放出体Qf时，放出前位于Qo处的移动体Qo移动到Q，根据质量守恒定律可建立移动体质量平衡方程式：

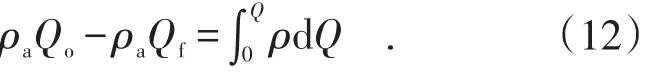
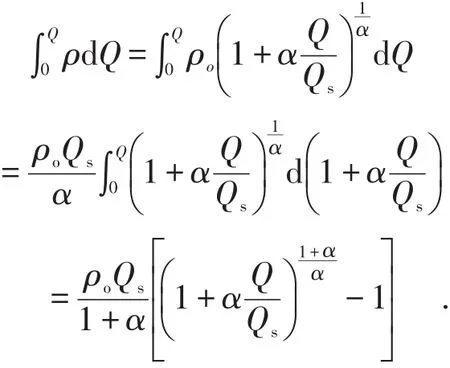
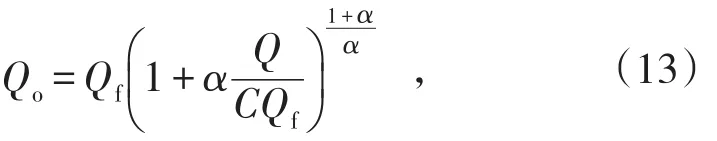
式（13）为类椭球体放矿理论的移动过渡方程，对式（13）两端进行微分运算得：

式（14）是根据速度阻滞系理论表达式和密度方程、移动过渡方程求得的速度阻滞系数。式（14）也正是类椭球体放矿理论创立时给出的速度阻滞系数，可见速度阻滞系数有充分的理论根据。

由式（14）可知，当 Q=0时，β=1；Q=Qs时β=0；0＜Q＜Qs时，1＞β＞0；Qs→∞ 时，β=1。该理论公式给出的结果与实验完全相符。

3.2 类椭球体放矿理论实际散体的速度方程

将式（4）、式（14）代入式（11）得到类椭球体放矿理论垂直下移速度方程：

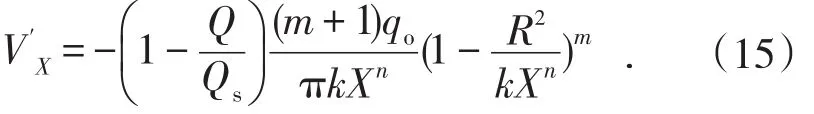
由实际散体速度的理论表达式（5）和速度阻滞系数式（14）得到类椭球体放矿理论实际散体径向速度V′R方程式。

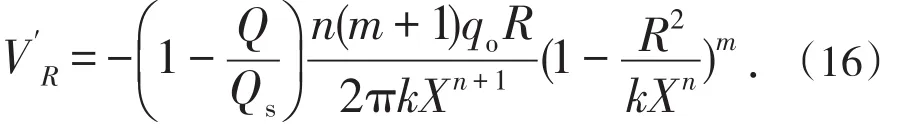
式（15）、式（16）表达的速度方程正是类椭球体放矿理论创立时给出的类椭球体放矿理论的实际散体速度方程。实际散体速度方程和密度方程都通过了理论和实验检验，成为类椭球体放矿理论体系重要的理论方程。

4 结论

通过上述的理论推导和分析，可到以下结论：

（3）根据速度阻滞系数理论表达式和密度方程、移动体质量平衡方程得到的速度阻滞系数为，它正是类椭球体放矿理论创立时给出的速度阻滞系数，论证为此提供了充分的理论依据。

（4）本研究构建的密度方程和实际散体速度方程与类椭球体放矿理论创立时给出的密度方程和实际散体速度方程完全相同，从理论上进一步证明了密度方程和实际散体速度方程都是正确的，能通过理论和实验检验。