两自由度减振镗杆系统的安全盆侵蚀与分岔

石建飞， 苟向锋， 张艳龙

(1. 天津工业大学 机械工程学院，天津 300387； 2. 兰州交通大学 机电工程学院，兰州 730070)

切削振动是影响加工表面质量和刀具耐用度的主要因素之一。近年来，学者对减振镗杆系统的模型和减振效果进行了研究,其中主要针对系统模型的简化及其参数优化。Andern等[1]建立了Euler-Bemoull减振镗杆模型。Andem和Meic等[2-3]采用新材料、新结构实现镗杆的减振。Evita等[4]设计了一种摩擦减振刀杆，利用刀杆的主结构与减振块接触面间的摩擦消耗振动能量，有效抑制了刀杆的振动。罗红波等[5]采用全局寻优数值搜索法和幅频响应曲线面积最小法对内置式减振镗杆动力学模型的参数进行了优化。赵永成等[6]实验研究了精镗孔时液膜阻尼对系统的减振效果，发现挤压液膜阻尼器在精镗加工时能提高孔加工质量。秦柏[7]用 ADAMS/ ANSYS仿真分析了减振镗杆各参数的影响。夏峰等[8]设计了一种新的约束阻尼性镗杆，并对该模型的参数进行了优化。刘立佳等[9]分析了减振镗杆振动控制的研究状况，指出减振镗杆减振技术在理论方面依然存在制约因素。目前很少有文献考虑减振镗杆系统在非线性因素下的减振效果，在减振镗杆系统中，减振块和镗刀杆之间由橡胶圈和阻尼液相连接，在建模过程中将橡胶圈和阻尼液转化为等效弹簧力和阻尼力时，其非线性因素的影响不可忽略，所以有必要对镗杆系统在非线性因素下的振动特性进行研究。

系统实际振动过程中最关心的是系统振荡的有界性问题。因为质点的运动振幅超过一定限度，往往会导致结构的破坏，从而产生了对安全盆的研究[10-12]。戎海武等[13]研究了谐和与噪声联合作用下Duffing振子的安全盆分岔与混沌，推导了系统的随机Melnikov过程，在随机扰动下系统的安全盆分岔点发生了偏移。Shang[14]研究了时滞位移反馈对Helmholtz振子系统的分形侵蚀安全域的控制，发现时滞量的增大能有效地抑制安全盆的侵蚀。葛根等[15]对形状记忆合金梁在简谐和白噪声联合激励下的混沌及安全盆侵蚀现象进行了研究，发现随机激励幅值的增大会增强安全盆的内部出现分形特性。然而对系统安全盆的研究主要针对单自由度系统安全盆的侵蚀及控制，对双自由度系统安全盆的侵蚀却少有研究。

本文建立两自由度减振镗杆系统的非线性动力学模型，研究系统在外激励频率和阻尼系数变化时安全盆的侵蚀和分岔现象。通过计算系统安全盆在侵蚀过程中的最大Lyapunov指数，分析系统安全盆出现分形侵蚀和边界侵蚀时其最大Lyapunov指数的变化特性。

1 减振镗杆系统的力学模型

减振镗杆系统由一个连续体和一个减振单元组成，如图1所示。镗杆的减振系统由大密度的减振块4和在减振块两端起支撑作用的橡胶圈2组成，减振块被阻尼液5所环绕。在加工过程中，镗杆振动所产生的动能将被其内部质量块4吸收，使得镗杆振动减小，改善了系统的切削状况。根据振动力学的理论分析可知，这样的系统建立方程很不方便，须进行简化[16]，将镗杆杆体1、两端垫片3、堵块6和刀头7作为主系统(连续体)；将两端橡胶圈2、减振块4和阻尼液5作为减振器(减振单元)。令M1为主系统质量，K1和C1分别为主系统的弹性系数和阻尼系数；M2为减振块4的质量，K2和C2分别为橡胶圈2的弹性系数和阻尼液5的阻尼系数。用集中质量法建立其简化的动力学模型如图2所示。图2中，由M1、K1、C1组成的系统称之为主系统，由M2、K2、C2组成减振器，Fcos(ΩT+φ)为系统外激励。

1.镗杆杆体；2.橡胶圈；3.垫片；4.减振块；5.阻尼液；6.堵；7.刀头图1 动力减振镗杆结构示意图Fig.1 Structure of dynamic damping boring bar

考虑减振器橡胶圈和阻尼液对振动系统非线性因素的影响，建立减振镗杆系统的运动微分方程如下：

(1)

(2)

(3)

方程(1)、(2)和(3)中，“··”和“·”表示对时间T分别求二阶导数和一阶导数。

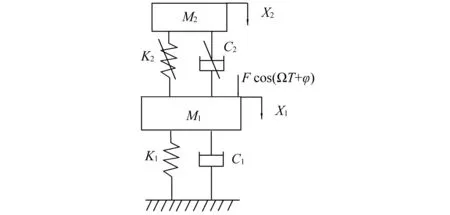
图2 减振镗杆系统的动力学模型Fig.2 dynamics model of damping boring bar system

(4)

式中

(5)

(6)

2 系统安全盆的侵蚀与分岔

系统的安全盆可由相空间的一个有界区域D来定义，使得以安全盆内部的点为起始点出发的轨线在时间趋于无穷大时仍在区域D内运动，构成了系统的安全解。即以安全盆外部的点为起始点出发的轨线在时间趋于无穷大时将逃逸出区域D，构成系统的不安全解，将导致系统结构的破坏与崩溃。安全盆的结构与某些吸引子的吸引域的结构相似[20]，当系统参数发生变化时，安全盆的面积和形状也将发生改变，即形成了安全盆的侵蚀。混沌运动也是有界的，安全盆内某些点为初值的运动是稳定周期运动或混沌运动。

2.1 安全盆的边界分形侵蚀与分岔

首先研究当ω变化时，系统安全盆的变化情况。选取系统参数M1=40 kg，M2=50 kg，F=112 N，C1=73 N·s/m，K1=0.44×106N/m，C2=303 N·s/m，K2=0.88×105N/m。将参数代入方程(1)，经计算得系统无量纲参数，如表1所示。

表1 系统无量纲参数取值表

(7)

并将该区域划分成个胞空间，将每个胞的中心点作为系统解的初始值。当系统通过这些初始值的解在足够长的时间如10 000时间单位内逃逸出区域D1，则认为此解是不安全；如果没有逃逸出区域D1，则近似的认为它是安全、有界的解。选取表1系统无量纲参数值，对于不同的ω，系统安全盆变化情况，如图3所示。

图3中的黑色部分代表导致系统安全解的初始值组成的部分，构成了系统的安全盆；而灰色部分则代表导致系统不安全解的初始值组成的部分。当ω=0.74时，系统在有界区域D1内均为安全解，在该区域内系统为完整的安全盆(即没有受到侵蚀)，如图3(a)。当ω增大至ω>0.740 6时，在有界区域D1内系统出现灰色区域，系统安全盆受到侵蚀。当ω=0.741时系统安全盆如图3(b)所示，此时系统安全盆已经被侵蚀。随着ω的增加，灰色不安全区域的面积不断增大，安全盆被侵蚀程度不断增强，如图3(c)所示。当ω>0.742 4时，系统安全盆如图3(d)所示，黑色安全盆边界变得不光滑，在黑色安全盆内出现了具有自相似结构的相互缠绕的灰色条纹，同样在灰色不安全区域内出现了具有自相似结构的相互缠绕的黑色条纹，通过盒子维方法[21]计算系统安全盆边界的分数维为1.432 5，表明系统安全盆出现边界分形侵蚀的现象。此时系统运动极不稳定，系统对初值极度敏感，初值的微小移动都将导致系统结构破坏或崩溃，在实际振动中应避免此类参数。随着ω继续增加，黑色安全域的面积不断增加，灰色不安全域的面积逐渐减小，但安全盆分形侵蚀的结构依然存在，而且随着ω的变化其分形结构也在不同程度的变化，如图3(e)～(h)所示。同样该参数对系统振动极为不利，容易引起系统结构的破坏。随着ω进一步增大，安全盆边界逐渐变得光滑，其自相似结构逐渐消失，系统分形侵蚀结构也不断退化消失，如图3(i)所示；当ω增加到0.748时，系统分形结构被完全侵蚀，此时系统安全区域面积不断减小，不安全区域面积不断增大，如图3(j)～(k)所示。计算发现当ω>0.751 6时，安全盆完全消失，即在有界区域D1内对任何初始值，系统解都是不安全的，如图3(l)所示。

由图3知，随着外激励频率ω的变化，系统安全区域发生丰富而又复杂的变化，安全盆也受到不同程度的侵蚀。如果将安全盆的突变现象(从完整的安全盆到侵蚀、直至完全消失)看作为一种分岔现象，将ω作为分岔参数，则ω1=0.740 6，ω2=0.742 4，ω3=0.751 6是系统的三个分岔点。即当ω<ω1时，系统安全盆没有被侵蚀，当ω>ω1时，安全盆被慢慢侵蚀，见图3(a)和3(b)；当ω<ω2时，系统安全盆没有出现分形侵蚀，当ω>ω2时，安全盆出现分形侵蚀，见图3(c)和3(d)；当ω<ω3时，系统安全盆没有完全消失，当ω>ω3时，安全盆完全消失，见图3(k)和3(l)。

图3 系统安全盆随ω的变化Fig.3 The erosion of safe basins of system via ω

由此可见，外激励频率ω的变化对系统安全盆的侵蚀过程以及分岔过程有重要的影响，是引起系统安全盆出现边界分形侵蚀的主要因素之一，也是影响系统振动安全性的主要因素之一。

2.2 安全盆的边界光滑侵蚀与分岔

(8)

并把此区域划分成500×500个胞空间，将每个胞的中心点作为系统解的初始值。选取表2系统无量纲参数值，对于不同的ζ2，系统安全盆变化情况如图4所示。

图4(a)为完整的安全盆图形。当ζ2增加至ζ2>0.247时，系统安全盆开始慢慢被侵蚀，如图4(b)～(d)所示，黑色安全域的面积不断减小，灰色不安全域的面积不断增加，安全盆被侵蚀的程度不断增强。随着ζ2的继续增加，黑色安全盆不断从左右两边侵蚀，使系统安全盆变成一条类似河流的黑色“窄带”，而且随阻尼系数ζ2的增加，安全盆变得越来越窄，如图4(e)～(h)所示，在有界区域D2内，系统在绝大部分区域内表现为不安全，而安全区域的面积变得非常小，甚至变成了一条曲线，见图4(h)。在此参数条件下，系统振动变得非常危险，在大部分区域内系统解都不安全。计算发现当ζ2>0.507时，系统安全盆被完全侵蚀，在整个有界区域D2内系统均表现为不安全解。

表2 系统无量纲参数取值表

由图4知，随ζ2的增大，系统经历了由完整安全盆到慢慢被侵蚀、最终到安全盆完全消失的过程。如果将安全盆的突变现象(从完整的安全盆到侵蚀、直至完全消失)看作为一种分岔现象，将ζ2作为分岔参数，则ζ2=0.247，ζ2=0.507是系统的两个分岔点。即当ζ2<0.247时，系统安全盆没有被侵蚀，当ζ2>0.247时，系统安全盆开始慢慢被侵蚀，见图4(a)和4(b)；当ζ2<0.507时，系统安全盆没有被完全侵蚀，见图4(h)，当ζ2>0.507时，系统安全盆完全被侵蚀。

图4 系统(4)安全盆随ζ2的侵蚀过程Fig.4 The erosion of safe basins of system (4) via ζ2

由此可见，阻尼液系数ζ2的变化同样对系统安全盆的侵蚀与分岔有重要影响。但在整个侵蚀过程中并没有出现具有自相似结构的分形边界，系统安全盆边界始终是光滑的，安全盆的侵蚀属于边界光滑侵蚀。下文根据系统最大Lyapunov指数研究安全盆出现边界分形侵蚀和边界光滑侵蚀的机理及其区别。

3 安全盆侵蚀的Lyapunov指数分析

安全盆的侵蚀意味着系统运动稳定性的破坏，而最大Lyapunov指数是判断系统运动是否稳定最直接、最有效的方法之一。对比图3，当ω=ω1=0.740 6时系统安全盆发生分岔，即安全盆开始被侵蚀，但在侵蚀过程中并没有出现分形侵蚀结构，选取表1中系统无量纲参数，取ω=0.74和ω=0.741分别计算其最大Lyapunov指数随迭代次数n的变化图如图5(a)和5(b)所示，图中采用了100 000次迭代，并将前40 000次迭代作为暂态予以略去(下同)，由图可见，在安全盆分岔前后其最大Lyapunov指数均小于零，表明此时系统安全盆受到侵蚀后并没有出现混沌运动。系统振动幅值不断扩大并逃逸出有界区域D1，导致系统安全盆受到侵蚀。

图5 分形侵蚀时系统最大Lyapunov指数Fig.5 The Top Lyapunov Exponent of the system with the change of iteration number n as fractal erosion

在图3中，当ω=ω2=0.742 4系统安全盆再次发生分岔，分岔后系统安全盆出现分形侵蚀结构，其它参数保持不变，分别取ω的值为0.742、0.742 4、0.743和0.744，计算其随迭代次数n变化时的最大Lyapunov指数如图5(c)所示，图中当ω=0.742时(即安全盆分岔前，系统安全盆没有出现分形侵蚀结构)，其最大Lyapunov指数仍小于零；当ω=0.742 4时系统安全盆发生分岔，其最大Lyapunov指数在零线附近上下波动；当ω=0.743时(即安全盆分岔后，系统安全盆出现分形侵蚀结构)，其最大Lyapunov指数大于零。经计算发现当系统安全盆出现分形侵蚀结构时，其最大Lyapunov指数始终大于零，而且分形侵蚀结构越复杂，其最大Lyapunov指数值越大。

当系统最大Lyapunov指数大于零时，系统出现混沌运动，意味着稳定流形和不稳定流行在Poincaré截面上横截相交，出现同宿分岔。由于同宿轨线断裂会引起安全盆边界的分形[22]，所以只有当系统最大Lyapunov指数大于零时，系统安全盆才可能出现分形侵蚀的结构。这与文献[13]根据Melnikov过程在均方意义上出现简单零点的条件给出系统安全盆出现分形侵蚀的临界值在结论上相一致。

对比图4，系统安全盆从两边边界不断被侵蚀，当ζ2=0.247时系统安全盆发生分岔，即系统完整的安全盆开始被侵蚀，但在侵蚀过程中系统边界始终是光滑的，没有出现自相似的分形结构。取表2系统无量纲参数，分别选取阻尼系数ζ2的值为0.24和0.25计算系统在分岔点前后其最大Lyapunov指数随迭代次数n的变化图如图6(a)和6(b)所示，由图知系统最大Lyapunov指数值在安全盆分岔前后均小于零，即系统安全盆受到侵蚀后并没有出现混沌运动；当ζ2=0.507时系统安全盆再次发生分岔，系统安全盆被完全侵蚀，同样在侵蚀过程中没有出现分形结构，保持其它参数不变，分别取ζ2=0.47和ζ2=0.51计算其随迭代次数n变化时的最大Lyapunov指数如图6(c)所示，由图知，即使系统安全盆被完全侵蚀，系统振动变得不安全，但其最大Lyapunov指数在安全盆分岔前后均小于零。经计算发现图4中在安全盆的侵蚀过程中，系统最大Lyapunov指数始终小于零。由此可见，系统安全盆在边界光滑侵蚀过程中并没有出现混沌运动，只是系统振动幅值有所扩大并跳出有界区域D2，导致系统安全盆受到侵蚀。

图6 边界侵蚀时系统最大Lyapunov指数Fig.6 The Top Lyapunov exponent of the system with the change of iteration number n as boundary erosion

综上所述，随系统参数的变化，在安全盆的侵蚀过程中，当系统最大Lyapunov指数大于零时，系统出现混沌运动，系统稳定流形和不稳定流行在Poincaré截面上横截相交，出现同宿分岔，同宿轨线的断裂导致系统安全盆出现边界分形侵蚀的结构。在安全盆边界光滑侵蚀过程中，系统相应最大Lyapunov指数始终小于零，安全盆边界光滑侵蚀是由系统振动幅值不断扩大并逃逸出有界区域而引起的，在此过程中系统并没有出现混沌运动，也没有出现同宿分岔。也就是说，在安全盆侵蚀过程中，只有当系统最大Lyapunov指数大于零时，系统才有可能出现分形侵蚀的结构。

4 结 论

本文考虑减振镗杆系统中橡胶圈和阻尼液的非线性因素对系统动力学特性的影响，建立了系统的非线性动力学模型。研究系统随外激励频率ω和阻尼系数ζ2变化时安全盆的侵蚀与分岔，结合最大Lyapunov指数对减振镗杆系统安全盆的侵蚀与分岔过程进行了分析，得到以下结论：

(1)随着外激励频率ω的增加，系统完整的安全盆逐渐侵蚀，在此过程中系统最大Lyapunov指数始终小于零，系统没有出现混沌运动；当ω增加到一定值时，系统最大Lyapunov指数大于零，系统稳定流形和不稳定流形在Poincaré截面上横截相交，出现同宿分岔，同宿轨线断裂导致安全盆边界出现分形侵蚀结构。

(2)随着阻尼系数ζ2的增加，系统安全盆由两边界不断被侵蚀并最终消失。在安全盆的侵蚀与分岔过程中，安全盆的边界始终是光滑的，系统没有出现边界分形侵蚀的结构，其最大Lyapunov指数始终小于零，系统没有出现混沌运动，只是系统振动幅值不断增大并跳出有界区域，导致系统安全盆被侵蚀，从而导致系统振动结构的破坏。

(3)当安全盆出现边界分形侵蚀时，系统出现混沌运动，其相应的最大Lyapunov指数大于零；当安全盆出现边界光滑侵蚀时，系统并没有出现混沌运动，其相应的最大Lyapunov指数始终小于零，只是振动幅值有所增大而已。此外，在判断安全盆是否出现分形侵蚀结构时，与Melnikov过程相比，本文通过计算系统Lyapunov指数给出系统出现分形结构的临界值的方法计算简单、方便，通用性强。本文的研究结果对减振镗杆的设计及参数优化有一定的理论参考价值。