动态凸包引导的偏优规划蚁群算法求解TSP问题

马学森，宫帅，朱建，唐昊



动态凸包引导的偏优规划蚁群算法求解TSP问题

马学森1,2，宫帅1，朱建1，唐昊3

（1. 合肥工业大学计算机与信息学院，安徽 合肥 230009；2. 广东三水合肥工业大学研究院，广东 佛山 528000；3. 合肥工业大学电气与自动化工程学院，安徽 合肥 230009）

针对蚁群算法搜索空间大、收敛速度慢、容易陷入局部最优等缺陷，提出一种基于动态凸包引导的偏优规划蚁群算法。改进后的算法动态控制蚂蚁的待选城市范围，有助于在跳出局部最优并向全局最优逼近的基础上减少蚂蚁搜索空间；同时，引入延陷漂流因子和基于待选城市构建的凸包来干预当前蚂蚁的城市选择，增加算法前期解的多样性并提高蚂蚁的偏优规划能力；再利用局部与整体相结合的完整路径信息、凸包的构建信息来协调信息素的更新，引导后继蚂蚁路径偏优规划，提高算法的求解精度；设计具有收敛性的信息素最大最小值限制策略，既加快算法的求解速度又避免算法过早停滞；最后在4种经典TSP模型上应用改进后的算法。仿真结果表明，所提算法在求解精度和收敛速度等方面均有显著提高，且具有较好的适用性。

蚁群算法；二维凸包；TSP；偏优规划

1 引言

TSP（travelling salesman problem）[1]又被称为旅行商问题，该问题具体描述为：有位旅行商需要访问个城市，他必须要走完所有城市，然后回到原点，每个城市只能选择一次，目标是形成一条最短路径。TSP作为一种经典NP难题，受到众多专家和学者的关注。他们利用组合优化提出很多启发式搜索算法，如遗传算法[2-3]、模拟退火算法[4]、人工神经网络[5]、禁忌搜索算法[6]、蚁群算法[7]、免疫算法[8]等。其中，蚁群算法作为一种仿生学算法，在20世纪90年代由Dorigo等[9-10]提出，由于它具有较好的分布式计算能力和较强的顽健性，同时易与其他算法融合，被广泛应用于一些NP难题的求解上。

蚁群算法是从自然界中蚂蚁觅食的群体行为得到启发而提出的，蚂蚁觅食时会在已走路径上释放信息素，信息素浓度越高的路径被后继蚂蚁选择的概率越大。蚁群算法求解TSP过程为：将只蚂蚁随机放到个城市节点上，每个蚂蚁按照一定的依据从没有访问过的城市中选择下一跳城市节点，同时每行走一步或完成整个城市访问后更新所有路径上的信息素浓度。

但蚁群算法求解时蚂蚁的城市选择范围较大，同时非优路径的多次出现和有些路径上的信息素会增加算法的迭代次数及收敛于局部最优解的概率。为弥补上述缺陷，本文基于二维凸包对蚁群算法进行改进，首先动态筛选蚂蚁的待选邻居城市节点，在有助于算法跳出局部最优的基础上，减少蚂蚁的城市选择范围；其次将延陷漂流因子和二维凸包融入城市选择策略，增加算法前期解的多样性，减少非优路径的出现并提高算法收敛速度；最后将完整的路径信息、二维凸包信息融入信息素更新策略，提高蚂蚁的路径寻优能力，并用改进的信息素最大最小值限制策略来进一步加快算法的收敛速度。

二维凸包对本文算法的作用体现为：利用每个当前城市节点与待选邻居节点构建的凸包区域范围之间的关系来影响蚂蚁下一跳城市节点的选择；当所有蚂蚁遍历完成，对迭代最优蚂蚁行走路径上的城市节点分别与其待选邻居节点再次构建凸包，通过构建的凸包及存在的凸包角（如图1(a)和图1(b)所示，其中，图1(b)不存在城市的凸包角）来获取蚂蚁遍历的方向与深度，协调后继蚂蚁的走向。将已构建凸包的区域范围与凸包角融入蚁群算法，更加有利于蚂蚁的行走与协作，并可以加快算法逼近于最优解。

最后，在Oliver30、Eil51、St70、Eil76这4个经典的TSP模型上验证具有收敛性的信息素最大最小值限制策略的有效性以及本文算法的精确性、收敛的快速性与适用性。其中，在Eil51上以迭代次数作为衡量指标对所提出的信息素最大最小值限制策略进行验证，同时延伸到其他3个TSP模型上也是有效的；以Oliver30和Eil51为例对本文算法的精确性和收敛的快速性进行详细验证，并引用到具有不同城市规模和位置的St70和Eil76中进行实验，进一步表明本文算法能在保证求解精度的基础上快速收敛，验证了本文算法的适用性。

2 相关工作

众多专家和学者针对蚁群算法的诸多缺陷进行了不同的改进研究。在信息素或节点选择策略方面[11-14]，文献[11]提出了一种释放在城市节点上的方向性信息素和探索因子，但没有考虑城市节点的位置及相对方向，随着城市规模的逐渐扩大，求解误差随之增加，同时收敛速度的提高并不显著。在最大最小蚂蚁系统方面[15-18]，文献[17]提出基于混沌的最大最小蚁群算法，采用tent混沌映射的方法产生初始信息素，当算法陷入长时间停滞状态时利用混沌映射扰动信息素，虽能扩大蚁群的搜索范围，但也进一步增加了算法的迭代次数。在图论优化蚁群方面[19-21]，文献[19]对整体TSP模型构建凸包，以凸包顶点作为蚂蚁出发点进行搜索，来减少算法的迭代次数，但该文只是对TSP模型进行凸包的构建，从而影响蚂蚁的初始位置分布，后续并没有把凸包融入蚁群算法，对蚁群算法本身没有实质性的改变。在蚂蚁多态方面[22-25]，文献[22]提出一种基于动态局部搜索的蚁群算法，为每个蚂蚁分配一个侦查蚁，增加蚂蚁局部搜索能力，并根据迭代效果动态更新信息素，但该算法实质上是动态增加参与迭代的蚂蚁数，并没有显著提高算法的求解精度。

在上述研究的基础上并针对其存在的缺陷，本文利用凸包的构建及构建的区域范围与凸包角，提出一种基于动态凸包引导的偏优规划蚁群算法（ACADCG, ant colony algorithm based on dynamic convex guidance），来求解TSP全部城市节点遍历问题。ACADCG限制蚂蚁下一跳的待选邻居节点范围，减小搜索空间，此外，随着蚂蚁待选邻居节点改变而动态变化的凸包（如图1(c)和图1(d)所示，其中，图1(d)存在的2个凸包分别为和,有助于算法跳出局部最优；ACADCG还引入延陷漂流因子来增加城市选择的随机性，提高算法前期解的多样性；同时将凸包的区域范围应用到蚂蚁选择城市节点概率式中，引导蚂蚁下一跳的偏优规划，减少交叉路径的出现；当所有蚂蚁遍历完，通过改进的路径信息、已构建的凸包及凸包角来修改信息素的更新规则，利用该规则来弱化导向非优解路径上的信息素及非优解包含的非优路径上的信息素，引导后继蚂蚁路径偏优规划，并引入与当前迭代次数相关的策略限制信息素上下限，进一步减少算法的迭代次数。

图1 凸包图

3 基于动态凸包引导的改进蚁群算法

本文针对蚁群算法搜索空间大、易陷入局部最优及收敛速度慢等缺陷，在蚂蚁的待选邻居城市范围、城市选择策略、信息素更新与控制策略上进行了改进。

3.1 待选邻居城市范围的控制

3.2 城市选择策略

3.2.1 延陷漂流因子

由于随着迭代次数的增加而递减，在初始阶段，蚂蚁选择城市的随机性大，会增加算法解的多样性。不过值最终变为非正数，蚂蚁按照本文所设概率计算式(3)进行选择后，信息素在最优路径上会持续增加，算法将最终收敛于最优解。

3.2.2 引导当前蚂蚁偏优规划的凸包

当蚂蚁位于城市时，如果下一跳城市与蚂蚁在上一跳城市时未遍历的待选邻居城市偏离较远，则蚂蚁后续可能会偏离这些未遍历的待选邻居城市，一旦持续偏离将引起蚂蚁折回遍历，而蚂蚁在折回遍历时极易产生交叉路径，降低解的精度。

为解决上述问题，本文提出引导当前蚂蚁偏优规划方法GCAPOP，用二维凸包引导蚂蚁下一跳城市的选择，使蚂蚁优先对最近已遍历城市凸包区域范围交集中未遍历的城市进行访问（不包括交集中边上城市节点），减少蚂蚁因折回遍历而可能引起的路径交叉（含有交叉路径的解为非优解）。其具体过程为：ACADCG算法中的蚂蚁位于城市时，需要从城市凸包的区域范围中（除城市外）选取下一个城市，当蚂蚁到达城市时，将需要再次从城市凸包的区域范围中（除城市外）选取下一跳城市，此时增加城市凸包与城市凸包区域范围交集C中城市被选为下一跳城市的概率，若蚂蚁依据概率选择城市，则具体采用轮盘赌的方式选出下一跳城市节点。传统蚁群算法中蚂蚁选择下一跳节点的概率如式(2)所示。ACADCG算法中蚂蚁选择下一跳节点的概率如式(3)所示。

基于GCAPOP方法的ACADCG算法增加了凸包区域范围交集中城市节点被选为下一跳节点的概率，提高了算法的收敛速度及解的质量，但并没有排除其他待选邻居节点被选择的可能，不会减少解的多样性，同时为了避免算法较易陷入局部最优，可利用本文所提的延陷漂流因子及改进的信息素更新策略。

3.3 信息素更新策略

ACADCG算法中的蚂蚁每行走一步便局部更新信息素，当所有蚂蚁一次遍历完成后，便全局更新信息素，最后对信息素范围进行控制。

3.3.1 引导后继蚂蚁偏优规划的凸包

图2 一次遍历中蚂蚁路径选择情况（Eil51）

为解决上述问题，提出引导后继蚂蚁偏优规划方法GSAPOP，将二维凸包融入信息素更新策略来弱化引起交叉的路径上的信息素及已形成交叉的路径上的信息素，引导后继蚂蚁路径选择，减少非优路径的产生。

算法每完成一次迭代，对迭代最优蚂蚁走过的路径进行信息素更新时，GSAPOP方法把更新分为2种情况（把迭代最优路径上的城市节点分别与其待选邻居节点构建凸包）。

2) 城市节点在凸包内部（图1(b)）。此时，按照式(8)中凸包内部的取值来更新城市节点与下个被选节点之间边的信息素。

ACADCG算法中GSAPOP方法会削减起始城市为凸点的交叉路径及引起交叉的路径（图2）上的信息素更新幅度，有利于后继蚂蚁向更优路径遍历。

3.3.2 偏优信息素更新

1) 信息素局部更新：蚂蚁从当前节点移动到下个节点后，利用式(4)更新路径边—上信息素。

采用信息素局部更新可以适度地减少蚂蚁所走过路径的信息素，使后继蚂蚁选中该路径的可能性减小，增加解的多样性，抑制算法过早停滞。

3.3.3 具有收敛性的信息素最大最小值限制区间

当信息素更新完成后，为了抑制由于边与边上信息素浓度差距过大而引起算法停滞现象的发生，本文引入信息素最大最小值限制策略。

含有传统公式的信息素最大最小值限制策略虽然能防止信息素过多地聚集在某些路径上，但一定程度上也抑制了算法收敛速度。本文将迭代次数考虑到信息素最大最小值限制策略中，对算法前期、中期及后期进行适当干预，既避免了因不同路径上信息素浓度差距过大导致算法陷入局部最优，又提高算法中后期向全局最优解逼近的概率。

改进后的最大信息素和最小信息素的取值分别如式(13)与式(14)所示，其中，式(14)的形式与传统公式相一致。

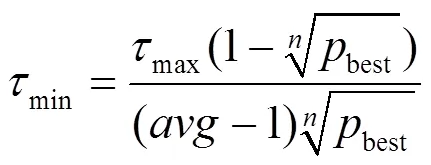
3.4 ACADCG算法的实现

ACADCG算法实现步骤如下，算法流程如图3所示。

5) 判断遍历是否完成。禁忌表中是否包含所有城市，若未包含则转步骤2)；否则转步骤6)。

6) 若只蚂蚁都构造完成各自的解，则转步骤7)；否则转步骤2)。

3.5 ACADCG算法复杂度

ACADCG算法复杂度包括时间复杂度与空间复杂度。

图3 ACADCG算法求解TSP流程

3.5.1 ACADCG算法时间复杂度

表1 本文蚁群算法的时间复杂度分析

3.5.2 ACADCG算法空间复杂度

4 仿真实验结果与分析

美国RAND公司将城镇的实际地理位置抽象成坐标节点，从而来构建经典的TSP标准数据库。众多专家和学者基本都以该库作为基础来测试所研究的近似求解算法，因此本文将ACADCG算法应用于标准数据库里的不同经典TSP模型（Oliver30、Eil51、St70、Eil76）中求解，来验证本文信息素最大最小值限制策略的有效性以及算法的精确性、收敛的快速性与适用性。算法开发环境为：在配有Intel 2.3 GHz，4 GB RAM的Windows 7 PC机上采用Java语言和Matlab开发了ACADCG算法，并对此算法进行了仿真实验测试。

4.1 算法参数

参数确定的具体过程和筛选原则如下。

表2 本文算法在4种TSP模型中相同参数值设置

表3 本文算法在4种TSP模型中不同参数值设置

4.2 信息素最大最小值限制区间对算法的影响

图4 3种不同信息素最大最小值限制区间算法收敛速度的比较

由图4所知，T-ACADCG算法的总体收敛速度比F-ACADCG算法快，而ACADCG算法相比T-ACADCG算法其收敛性又进一步提升。F-ACADCG算法和T-ACADCG算法分别在830多次和760多次收敛到最优解，而ACADCG算法在700次左右就已经收敛到最优解了。

T-ACADCG算法中的信息素最大最小值限制范围的上下限会随着解的改变而变化，相比于固定上下限的F-ACADCG算法收敛速度要快。但T-ACADCG算法中的上下限有时会减慢算法向最优解逼近，而本文中信息素最大最小值限制范围的上下限相比于T-ACADCG算法中的上下限会在算法迭代中期，随着迭代的推移平稳增加，能适当减少较优路径上信息素递增幅度的限制，增加算法逼近于最优解的概率；在算法后期，相比于T-ACADCG算法中的上下限其倍数的增量非常缓慢直至不变，本文中信息素最大最小值限制范围的上下限随着算法的迭代，避免不同路径上信息素差别过大；但在算法前期，本文中信息素最大最小值限制范围的上下限与T-ACADCG算法中的上下限变化相似，以抑制算法前期解的多样性。将上述不同策略的ACADCG算法拓展到4.4节中的Oliver30、St70、Eil76中进行仿真实验，变化趋势与图4相似，在此不再重复绘图与分析。

4.3 ACADCG算法对收敛速度的影响

仍以Eil51作为详细分析对象来测试本文算法的收敛速度。将蚁群系统（ACS, ant colony system）、最大最小蚂蚁系统（MMAS, max-min ant system）、基于方向信息素协调的蚁群算法[11]（AADC, ant algorithm based on direction-coordinating）和本文ACADCG算法进行寻优结果比较，实验结果如图5所示。

图5 4种算法收敛速度的比较

由图5可知，ACS算法、MMAS算法、AADC算法在迭代400次之后开始逐步收敛，分别在迭代1 400次左右、1 200次左右、1 000次左右才能最终收敛；ACADCG算法在迭代700多次，就收敛到429.18，逼近于理论最优解426。因此，ACADCG算法收敛速度有显著提高，求解精度也有进一步的改进。将4.4节中的Oliver30、St70、Eil76作为仿真对象测试上述不同算法，变化趋势与图5相似，在此也不再重复绘图与分析。

针对收敛速度的问题，本文以Oliver30和Eil51为例，将ACADCG算法与ACS算法、MMAS算法、AADC算法进行仿真实验比较，结果如表4所示。表4中结果均为30次实验所得。为避免赘述，St70、Eil76的仿真实验结果将在4.4节中详细列出。

表4 ACADCG算法与其他算法收敛速度上下限对比

求解快速性的主要原因是：ACADCG算法中的蚂蚁是从当前所有剩余城市中筛选出若干个城市作为待选邻居城市集合，缩小了搜索空间。此外，待选邻居城市集合的动态扩充有助算法在陷入局部最优时跳出局部最优，加快算法的收敛速度；当蚂蚁进行城市选择时，GCAPOP方法增加了凸包区域范围交集中城市被选概率，使蚂蚁优先访问最近已遍历城市附近未选择的城市节点，增加蚂蚁向无交叉路径解逼近的概率，推动ACADCG算法向全局最优解逼近；当所有蚂蚁完成遍历后，含有GSAPOP方法的信息素更新策略能削弱非优路径及其周边路径上的信息素，提高后继蚂蚁向较优路径集合逼近的概率，加快算法寻优过程中的收敛速度；同时，本文的信息素最大最小值限制策略能对算法进行适当的干预，进一步减少了算法的迭代次数。

4.4 ACADCG算法在多种模型中综合性能分析

将ACADCG算法与其他蚁群算法分别应用于4个典型TSP模型中进行误差率、收敛速度、适用性等综合性能仿真实验，结果如表5所示。此外，ACADCG算法在4个模型上求解获得的最优路径如图6所示。

图6 ACADCG算法最优路径遍历结果

表5 典型TSP问题求解对比模型

ACADCG算法引入了二维凸包，而二维凸包的构建与城市节点的位置相关，因此具有不同城市节点位置和城市数量的TSP模型，其求解误差可能不一样，但ACADCG算法的误差控制能力优于与其对比的算法且收敛速度较快，主要原因是：本文算法能有效避免蚂蚁在TSP模型中遍历时出现交叉路径，提高了算法的整体求解精度和收敛速度。同时，本节4个TSP模型上的仿真结果也体现了ACADCG算法具有较好的适用性。

5 结束语

针对蚁群算法搜索空间大、求解精度差、迭代轮数多的缺陷，本文基于二维凸包对蚁群算法进行了改进。通过仿真对比分析可知，改进后的蚁群算法全局搜索能力得到提高，收敛速度进一步加快，而且在此过程中，能够较好地克服算法过早收敛到局部解的缺点，同时能够得到更精确解，且具有较好的适用性。实验结果表明，本文所提出的改进是切实可行的。

然而本文算法还存在一些不足之处，首先蚁群算法的随机性和凸包构建的动态性导致了算法复杂度的不确定性；其次凸包的构建有一定的代价，但本文不把凸包构建作为影响算法的性能指标，因凸包构建的代价不影响算法的迭代次数。未来，将深入分析和探讨凸包构建，以便进一步提高算法的性能，并将算法应用于数据规模更大的问题上来进行求解。

[1] DORIGO M, GAMBARDELL L M. Ant colonies for the travelling salesman problem[J]. Bio Systems, 1997, 43(2): 73-81.

[2] MAEKAWA K, TAMAKI H, KITA H, et al. A method for the traveling salesman problem based on the genetic algorithm[J]. Transactions of the Society of Instrument & Control Engineers, 1995, 31(5): 598-605.

[3] WANG J, ERSOY O K, HE M, et al. Multi-offspring genetic algorithm and its application to the traveling salesman problem[J]. Applied Soft Computing, 2016, 43(3): 415-423.

[4] MURRAY A T, CHURCH R L. Applying simulated annealing to location-planning models[J]. Journal of Heuristics, 1996, 2(1): 31-53.

[5] YU D, JIA J. A neural network algorithm with optimized parameters and used to solve the TSP[J]. Acta Electronica Sinica, 1993, 21(7): 16-22.

[6] LIN Y, BIAZ Z, LIU X. Developing a dynamic neighborhood structure for an adaptive hybrid simulated annealing – tabu search algorithm to solve the symmetrical traveling salesman problem[J]. Applied Soft Computing, 2016, 49(9):937-952.

[7] LIU Z, LI X, WANG H. Improvement of self-adaptive ant colony algorithm based on cloud model[J]. Computer Engineering and Applications, 2016, 52(19): 68-71.

[8] PAN G, LI K, OUYANG A, et al. Hybrid immune algorithm based on greedy algorithm and delete-cross operator for solving TSP[J]. Soft Computing, 2016, 20(2):555-566.

[9] DORIGO M, MANIEZZO V, COLORNI A, et al. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems Man and Cybernetics-Part B, 1996, 26(1): 29-41.

[10] DORIGO M, GAMBARDELLA L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 53-66.

[11] 孟祥萍, 片兆宇, 沈中玉, 等. 基于方向信息素协调的蚁群算法[J]. 控制与决策, 2013, 28(5): 782-786.

MENG X P, PIAN Z Y, SHEN Z Y, et al. Ant algorithm based on direction-coordinating[J]. Control and Decision, 2013(5): 782-786.

[12] 吴华锋, 陈信强, 毛奇凰, 等. 基于自然选择策略的蚁群算法求解TSP问题[J]. 通信学报, 2013, 34(4): 165-170.

WU H F, CHEN X Q, MAO Q F, et al. Improved ant colony algorithm based on natural selection strategy for solving TSP problem[J]. Journal on Communications, 2013(4): 165-170.

[13] 林建兵, 陈智雄, 姚国祥. 一种基于域密度的蚁群系统(AS)改进算法及结果解析[J]. 武汉大学学报(工学版), 2016, 49(4): 627-634.

LIN J B, CHEN Z X, YAO G X. An improved AS algorithm and result analyzing based on domain and its density[J]. Engineering Journal of Wuhan University, 2016, 49(4): 627-634.

[14] 马学森, 曹政, 韩江洪, 等. 改进蚁群算法的无线传感器网络路由优化与路径恢复算法[J]. 电子测量与仪器学报, 2015, 29(9): 1320-1327.

MA X S, CAO Z, HAN J H, et al. Routing optimization and path recovery algorithm in wireless sensor network based on improved ant colony algorithm[J]. Journal of Electronic Measurement and Instrument, 2015, 29(9): 1320-1327.

[15] 孙力娟, 王良俊, 王汝传. 改进的蚁群算法及其在TSP中的应用研究[J]. 通信学报, 2004, 25(10): 111-116.

SUN L J, WANG L J, WANG R C, Research of using an improved ant colony algorithm to solve TSP[J]. Journal on Communications, 2004, 25(10): 111-116.

[16] BU Y, LI T Q, ZHANG Q. A weighted max-min ant colony algorithm for TSP instances[J]. IEICE Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2015(3): 894-897.

[17] 耿志强, 邱大洪, 韩永明. 基于混沌的MMAS算法及其在旅行商问题中的应用[J]. 计算机工程, 2016, 42(3): 192-197.

GENG Z Q, QIU D H, HAN Y M. Max-min ant system algorithm based on chaos and its application in TSP[J]. Computer Engineering, 2016, 42(3): 192-197.

[18] WANG Y. Hybrid max-min ant system with four vertices and three lines inequality for traveling salesman problem[J]. Soft Computing, 2015, 19(3): 585-596.

[19] 张层. 基于二维凸包的改进蚁群算法求解TSP问题[D]. 广州: 华南理工大学, 2013.

ZHANG C. An improved ant colony algorithm based on two-dimensional convex hull for TSP[D]. Guangzhou: South China University of Technology, 2013.

[20] 党小超, 李小艳. 基于图论的WSN节点定位路径规划[J]. 计算机工程, 2012, 38(11): 100-103.

DANG X C, LI X Y. WSN node localization path planning based on graph theory[J]. Computer Engineering, 2012, 38(11): 100-103.

[21] PRAGYA, DUTTA M, PRATYUSH. TSP solution using dimensional ant colony optimization[C]//International Conference on Advanced Computing & Communication Technologies. 2015: 506-512.

[22] QIN H, ZHOU S, HUO L, et al. A new ant colony algorithm based on dynamic local search for TSP[C]//International Conference on Communication Systems and Network Technologies. 2015: 913-917.

[23] GU S, ZHANG X. An improved ant colony algorithm with soldier ants[C]//2015 11th International Conference on Natural Computation (ICNC). 2016: 205-209.

[24] LUO W, LIN D, FENG X X. An improved ant colony optimization and its application on TSP problem[C]//2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). 2017: 136-141.

[25] 盛国军, 温涛, 郭权, 等. 基于改进蚁群算法的可信服务发现[J]. 通信学报, 2013, 34(10): 37-48.

SHENG G J, WEN T, GUO Q, et al. Trustworthy service discovery based on a modified ant colony algorithm[J]. Journal on Communications, 2013, 34(10): 37-48.

[26] 詹士昌, 徐婕, 吴俊. 蚁群算法中有关算法参数的最优选择[J]. 科技通报, 2003, 19(5): 381-386.

ZHAN S C, XU J, WU J. The optimal selection on the parameters of the ant colony algorithm[J]. Bulletin of Science and Technology, 2003, 19(5): 381-386.

Ant colony algorithm of partially optimal programming based on dynamic convex hull guidance for solving TSP problem

MA Xuesen1,2, GONG Shuai1, ZHU Jian1, TANG Hao3

1. School of Computer and Information, Hefei University of Technology, Hefei 230009, China 2. Research Institute of Sanshui & Hefei University of Technology in Guangdong, Foshan 528000, China 3. School of electrical and Automation Engineering, Hefei University of Technology, Hefei 230009, China

To solve basic ant colony algorithm’s drawbacks of large search space, low convergence rate and easiness of trapping in local optimal solution, an ant colony algorithm of partially optimal programming based on dynamic convex hull guidance was proposed. The improved algorithm dynamically controlled the urban selection range of the ants, which could reduce the search space of ants on basis of helping the algorithm to jump out of local optimal solution to global optimal solution. Meanwhile, the delayed drift factor and the convex hull constructed by the cities to be chosen were introduced to intervene the current ants’ urban choice, it could increase the diversity of the early solution of the algorithm and improve the ability of ants’ partially optimal programming. Then the pheromone updating was coordinated by using construction information of convex hull and the complete path information that combined local with whole, it could improve the accuracy of the algorithm by guiding the subsequent ants to partially optimal programming. The pheromone maximum and minimum limit strategy with convergence was designed to avoid the algorithm’s premature stagnation and accelerate the solving speed of the algorithm. Finally, the proposed algorithm was applied to four classic TSP models. Simulation results show that the algorithm has better optimal solution, higher convergence rate and better applicability.

ant colony algorithm, convex hull, TSP, partially optimal programming

TP18

A

10.11959/j.issn.1000−436x.2018218

马学森（1976−），男，安徽庐江人，合肥工业大学副教授、硕士生导师，主要研究方向为无线传感器网络、嵌入式系统、大数据处理、网络与信息安全。

宫帅（1993−），男，安徽滁州人，合肥工业大学硕士生，主要研究方向为无线传感器网络、物联网、网络与信息安全。

朱建（1992−），男，安徽五河人，合肥工业大学硕士生，主要研究方向为高可靠性嵌入式系统、无线传感器网络、物联网。

唐昊（1972−），男，安徽庐江人，合肥工业大学教授、博士生导师，主要研究方向为离散事件动态系统、随机决策与优化理论、强化学习等智能优化与控制方法、自动化生产线、物联网和微网等系统优化设计与控制技术。

2017−07−17；

2018−07−02

国家自然科学基金资助项目（No.61573126）；广东省科技发展专项基金资助项目（No.2017A010101001）；中央高校基本科研业务费专项基金资助项目（No.JZ2016HGBZ1032）；国家留学基金资助项目

The National Natural Science Foundation of China (No.61573126), The Special Funds for Science and Technology Development of Guangdong Province (No.2017A010101001), The Central University Basic Business Expenses Special Funding for Scientific Research Project (No.JZ2016HGBZ1032), China Scholarship Council Foundation