基于三维激光点云的城市绿化树种材积及树干碳储量无损精确测算

徐诗宇， 施拥军， 冯晟斐

（1.浙江农林大学 亚热带森林培育国家重点实验室，浙江 杭州311300；2.浙江农林大学 浙江省竹资源协同创新中心，浙江 杭州 311300；3.浙江农林大学 浙江省森林生态系统碳循环与固碳减排重点实验室，浙江 杭州311300；4.浙江农林大学 环境与资源学院，浙江 杭州 311300）

城市森林是森林碳储量的重要组成部分之一，对调节局部乃至全球水平的气候变化起着重要作用。绿化树种在城市森林的碳吸收、碳固存中占主导地位，其中树干约占乔木总碳储量的58.2%［1］。城市绿化树种的树干干形在复杂的环境条件和频繁的人为干扰下相比野外林分存在一定差异，传统的基于野外林分调查拟合的材积模型及树干碳储量模型并不能很好地与之相匹配［2－3］；并且城市绿化树种因具有生态景观、保护生物多样性等生态功能［4－6］，观赏经济价值较高，不宜通过伐倒收获进行研究。因此，无损精确地测算立木材积及树干碳储量对于评估城市森林碳汇功能以及城市森林对于缓减气候变化的贡献具有重要意义。三维激光扫描技术又称地面激光扫描技术（terrestrial laser scanning，TLS），是一种能够采集目标物体表面的三维坐标和反射强度等数据，并最终以点云形式表达在计算机上的技术［7－10］。在现有的 TLS 在林业调查领域的研究中， LIANG 等［11］、 梁子瑜［12］、 尤磊［13］虽然利用建模法［13－15］和干曲线法［11－12］测算了干形通直的杉木Cunninghamia lanceotala材积，并通过与实际量测或通过材积方程测算得到的材积进行简单的比较分析，揭示了TLS在树干材积测算方面的巨大潜力。采用不同分段间隔对立木材积测算精度的影响，以及TLS在测算树干碳储量方面的潜力等研究并未有后续深入地展开。无患子Sapindus mukorossi为落叶阔叶乔木，树干通直、枝叶广展，是中国长江流域以南地区极为常见的城市绿化树种之一。本研究基于TLS结合局部采样的方法对无患子立木材积以及树干碳储量进行无损测算研究，旨在探索TLS在测算城市绿化树种材积及树干碳储量的方面潜力，分析不同区分段长度对立木材积及碳储量计算精度的影响，找出适用于材积测算的区分段长度并分析城市绿化树种树干与野外林分的异同，为中国城市绿化树种固碳能力的测算及生物量扩展因子（BEF）的研究提供依据。

1 研究区概况及研究方法

1.1 研究区概况

研究区域位于浙江省杭州市临安区的浙江农林大学校园（29°56′～30°23′N， 118°51′～119°52′E）。 研究区为典型的亚热带季风气候，四季分明；年平均气温为16.0℃，年降水量为1 614.0 mm，无霜期为237.0 d，全年光照充足。研究区有无患子，银杏Ginkgo biloba，玉兰Magnolia denudata等城市常用绿化树种；植被覆盖率高，种类丰富，人为干扰强，是典型的城市绿地类型。

1.2 TLS扫描原理及扫描特点简介

使用的Leica ScanStation C5脉冲式三维激光扫描仪主要通过激光器不断发射脉冲信号，通过接收接触物体表面后返回的信号计算飞行时间，结合相应信号发射时的水平角和竖直角，得到并记录目标的三维坐标点云数据。TLS特点：①精准高效。TLS在低精度下完成单测站360°×270°的全景扫描仅需2～3 min。TLS在1.50～50.00 m测距范围内采集点云数据的点位精度为±6.0 mm，测距精度为±1.0 mm。②无损。TLS通过非接触性激光对目标进行测量，不会对立木以及周边的环境产生任何影响及破坏，可以实现对立木的动态监测。③信息丰富。TLS是对目标表面的致密精细化测量，得到的点云数据具有极高的还原度，可以提取树高、胸径等丰富的测树信息。

1.3 点云数据获取与样本采集

于2017年7月利用Leica ScanStation C5脉冲式三维激光扫描仪进行了单立木三维点云的采集工作。在进行点云数据采集前，以5.00 cm为起测胸径分别用胸径尺和全站仪悬高测量法对实验区内所有无患子的胸径、枝下高、树高进行测量，按《原木材积表》中所规定的2.00 cm为一径阶对无患子进行径阶的划分与统计，采用径阶等比法按比例从各径阶中选取无患子共计30株进行实验（径阶分布如图1），由于径阶10.00 cm以下（18.00 cm以上）的样本过少，因此将10.00 cm以下（18.00 cm以上）的立木划分到18.00 cm（18.00 cm）径阶中。在选取无患子样本后，进行点云数据的采集。采集方法：本研究中为获取完整的单立木点云数据，无患子都经过3～4站·株－1的扫描，相应测站的布设近似呈等边三角形或矩形分布。并且根据地形及布设测站的通视情况，在目标立木周围放置3个公共参考标靶，确保在不同的测站都能被完整扫描到。在完成测站及标靶地布设后，进行仪器地架设并整平，并将扫描参数设置如下：扫描范围采用单立木窗扫描，即用户自定义扫描范围；采用低分辨率，并在设置相应的保存文件夹后开始扫描。扫描过程中平均扫描时间约为 10 min·株－1·站－1［16］。

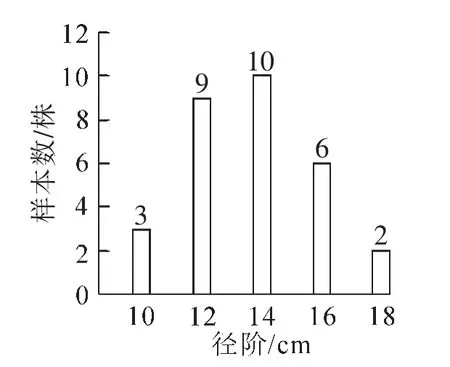
图1 无患子样木的径阶分布Figure 1 Diameter grade distribution of Sapindus mukorossi samples

待样本点云数据采集完成后，在各径阶内选取3株标准木（若数量不满3株则取该径阶内全部立木），利用直径5.15 mm的瑞典手持式取芯器CO250分别在树干基部处、树高1.00 m处及1.30 m对样木钻芯进行取样，并用游标卡尺量测记录钻孔孔径［17］。将样本分径阶装袋带回实验室中，置于100℃下烘干至恒量（间隔2.0 h 2次称量所得的样本质量差不超过0.5%即视为恒量），用0.000 1 g精密电子天平称取各径阶的钻芯总干质量［18］；利用取芯器标定的直径与记录孔径的均值作为圆柱模型的截面直径计算钻芯体积，将计算得到的均值作为该径阶的树干生物量密度。

1.4 数据预处理及基本测树因子提取

点云数据预处理及部分测树因子的提取在Cyclone软件中完成。点云数据的预处理主要包括以下几个方面：①坐标配准。利用每个测站所采集的3个公共标靶的信息可将不同测站的单立木（枝叶样本）点云数据匹配到同一坐标系下。②点云拼接。通过软件中点云拼接（unify cloud）功能将原本各测站独立的点云数据拼接成一个完整点云，并舍去重复的点和距离小于设定阈值的点（默认1.0 mm），从而减小数据冗余。点云拼接误差为1.0～2.0 mm。③点云去噪。依靠人工判别剔除在单立木点云数据采集过程中产生的噪声点、孤立点以及无用的地面点。

提取的单立木基本测树因子包括树高、枝下高以及胸径。其中：树高采用单立木三维点云坐标中的高程直方图提取；枝下高通过在点云图像中依靠人工判别获取树冠起始位置的高程值并结合高程直方图提取［19－20］；干径、胸径则采用最小二乘圆拟合算法对立木胸高处（距水平地面1.30 m）厚度为2.00 cm的切片点云进行拟合后提取［21－23］。

1.5 基于三维点云的树干材积及碳储量测算方法

基于三维激光点云的材积测算方法采用精细区分段求积法：将树干点云以固定间距进行分段，通过最小二乘圆拟合算法提取各分段截面直径，采用圆台模型测算各分段体积，汇总后得到立木材积VS。碳储量CS则用材积VS与树干单位体积生物质量ρS及含碳率的乘积进行测算。

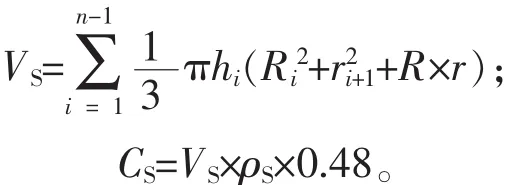
其中：VS表示立木材积；hi表示分段间隔；Ri表示下截面半径；ri表示上截面半径。

1.6 树干材积及碳储量参考值测算方法

采用浙江省全省通用的阔叶树二元材积模型计算立木材积模型值VS2；而一元材积模型因受地域影响较大，因此，采用浙江省浙西北丘陵山区专用的一元材积模型计算立木材积模型值VS1［24］，计算公式如下所示。碳储量测算方法则与上述2.4节中基于三维点云的树干碳储量测算方法相同。

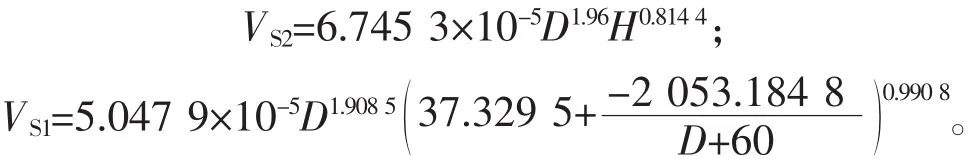
其中：D为胸径；H为树高。

树干碳储量参考值CS采用基于第7次全国森林资源清查资料的《中国森林植被生物量和碳储量评估》中的其他硬阔叶树类单立木碳储量模型。计算公式如下：

其中：D为胸径；H为树高；CMS表示树干碳储量（去皮）；CMP表示树皮碳储量。

1.7 单因素方差分析及精度评估方法

使用Excel 2010和SPSS 20.0进行单因素方差分析（one-way ANOVA）检验不同处理方法间的差异显著性，显著性水平设定为α＝0.05。并采用标准误差（ERMSE）和乖离率（sbias）检测不同处理方法间的误差。计算公式如下：

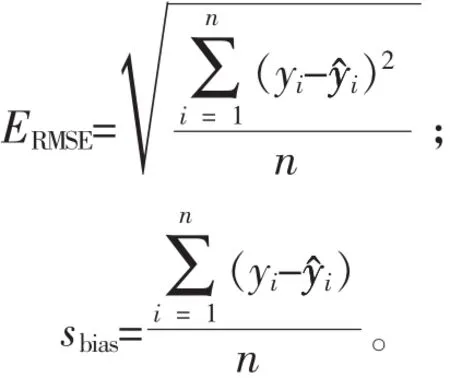
其中：y表示TLS测算值；y＾表示实测值。

2 结果与分析

2.1 基本测树因子的提取及分析

对基于TLS测算的不同径阶共计30株无患子的树高与胸径数据与实测值进行比较（图2），发现两者均具有极高的精度。其中，胸径标准误差（ERMSE）为±0.34 cm，平均相对误差为1.97%；树高标准误差（ERMSE）为±0.36 m，平均相对误差为4.58%。

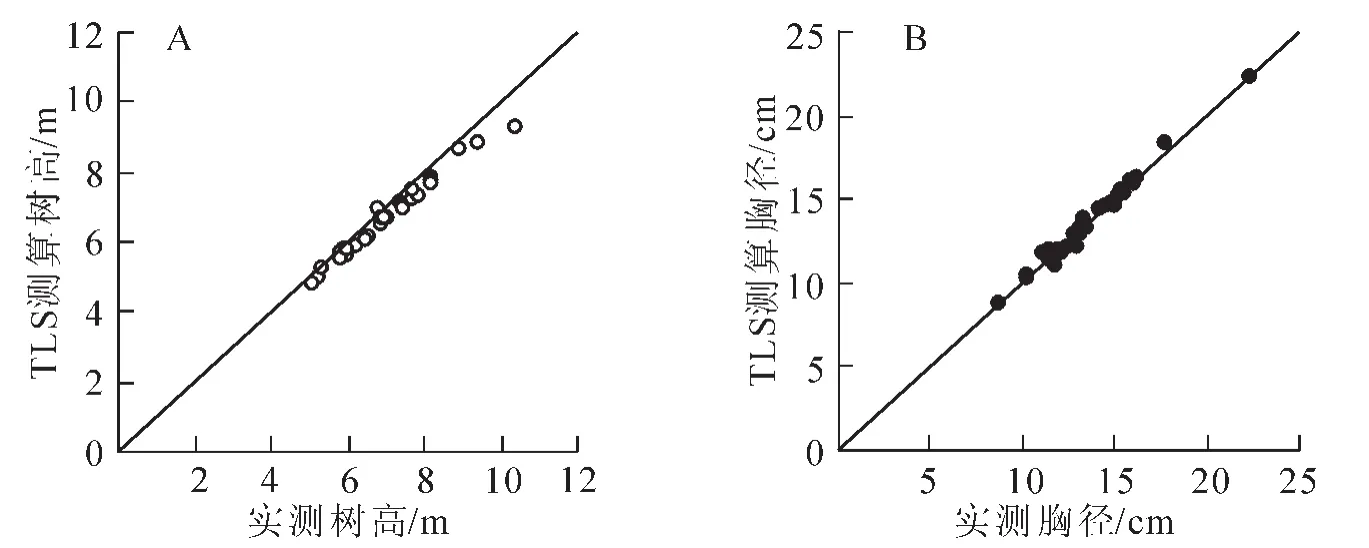
图2 TLS提取的胸径、树高与实测值比较Figure 2 Comparison of diameter and height extracted base on TLS with actual measurement

2.2 不同区分段长度对材积测算的影响分析

在以0.10 m区分段长度计算的材积值作为标准值的前提下（本研究中在对不同方法测算的材积、碳储量精度的比较中，均以此为前提），由表1可见：30株无患子利用不同区分段长度计算得到的材积均值变化范围为37.93～40.10 dm3，其中各区分段长度计算材积值的标准误差（ERMSE）变化范围从最低的0.44dm3到最高的2.79 dm3，变化幅度并不明显，各区分段长度测算得到的材积值之间均无显著差异（P＞0.05）。 乖离率（sbias）变化范围则从最低的0.02 dm3到最高的2.17 dm3，表明随区分段长度增加，测算的材积值逐渐偏离真实值。

表1 不同区分段长度下测算的材积比较Table 1 Comparison of volume measured based on different section lengths

由图3可见：当区分段长度≤0.40 m时，材积测算误差集中、近似呈正态分布，材积测算精度高且稳定；而当区分段长度由0.40 m变为0.50 m时，平均误差及误差离散度迅速变大；当区分段长度大于0.50 m时，随着区分段长度的增加，平均误差及误差离散度持续变大，在区分段长度为1.00 m时达到最大。说明随着区分段长度的增加，测算的立木材积更易偏离真值，出现异常情况如：区分段长度为0.60 m下的普通异常点whz10和whz17，极端异常点whz16以及区分段长度为0.80 m下的普通异常点whz19和whz26。

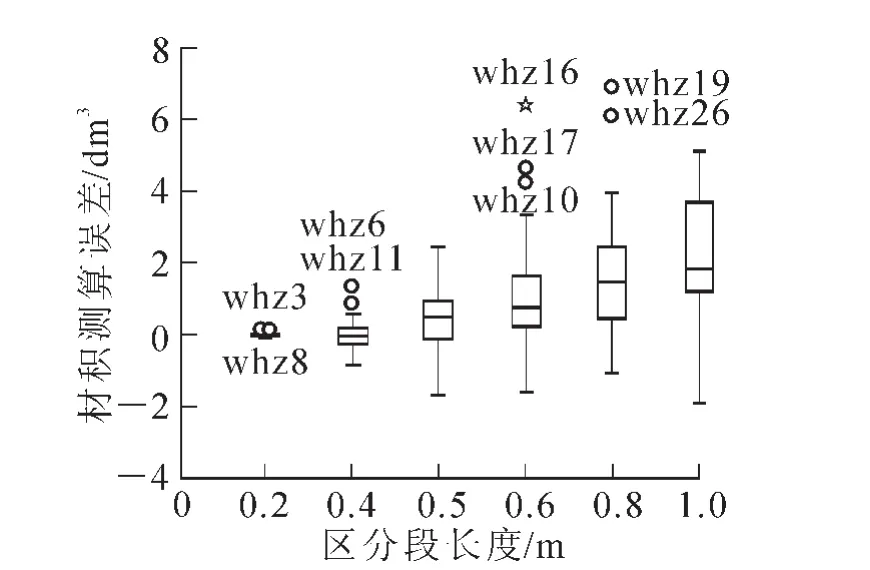
图3 不同区分段长度下材积测算误差的分布及比较Figure 3 Distribution and comparison of volume measurement error in different section lengths

2.3 立木材积、碳储量不同测算方法比较

表2对基于4种不同方法测算的30株无患子立木材积进行方差分析，发现利用现有一元材积模型和二元材积模型测算的立木材积之间并无显著差异（P＞0.05）。但基于一元材积模型和二元材积模型测算的立木材积却均要显著高于基于TLS区分求积得到的立木材积（P＜0.05）。其中，利用一元材积模型测算的材积值最高（68.77 dm3±36.58 dm3），分别是以0.10 m为区分段长度测算的材积值（37.93 dm3±10.97 dm3）的1.67倍和以1.00 m为区分段长度测算的材积值（40.10 dm3±11.57 dm3）的1.58倍，可见利用一元材积模型测算城市绿化树种材积误差之大。相比较而言，利用二元材积模型测算的材积值（54.54 dm3±31.91 dm3）与以区分求积得到的材积值之间的差距要小的多。

利用5种不同方法测算的30株无患子CS之间也存在不同程度的差异：其中利用一元材积模型测算的CS（22.26 kg±11.80 kg）最高，并与其他方式测算的CS存在显著差异（P＜0.05）。而二元材积模型以及树干碳储量模型测算的CS（17.64 kg± 10.25 kg， 17.92 kg± 9.59 kg）与以1.00 m为区分段长度测算的CS（13.09 kg±5.77 kg）之间无显著差异（P＞0.05），但均要显著高于以0.10 m为区分段长度测算的CS（12.38 kg ± 5.64 kg）（P＜0.05），表明利用二元材积模型和碳储量模型仅能实现CS的粗略测算。本研究中利用材积模型测算CS是以材积与树干生物量密度以及含碳率的乘积实现的，但研究发现利用二元材积模型测算的CS与一元材积模型测算的CS之间存在显著差异，而与以1.00 m为区分段长度测算的CS之间并无显著差异，这与上述研究中材积显著性差异的表现并不一致。

表2 不同方法测算的材积、树干碳储量比较Table 2 Comparison of volume and stem carbon storage measured by different methods

图4A将现有模型测算的材积和作为标准值的基于TLS测算的材积进行比较发现：利用现有模型测算的材积在立木自身材积较小时具有较高精度，但随着立木自身材积的不断增大，模型测算的立木材积逐渐开始偏离参考线y＝x，即精度不断下降，并且偏离速度随材积的增大逐渐变快。由图4B可见：利用现有模型测算的立木CS精度在随立木自身CS变化的趋势上与利用模型测算的立木材积精度具有一致性——即利用现有模型测算的CS在立木自身CS较小时具有较高精度，但随着立木自身CS的不断增大，模型测算的CS逐渐开始偏离参考线y＝x，即精度不断下降，并且偏离速度随CS的增大逐渐变快。表明利用现有模型测算的材积和CS精度随立木的生长在总体上呈下降趋势。而一元材积模型测算的材积和CS精度均为现有模型中最差。

3 讨论与结论

3.1 讨论

基于不同区分段长度测算的立木材积值之间并没有显著差异，说明在对精度没有较高要求的研究或调查中，≤1.00 m的区分段长度均可满足立木材积测算的需要，这与传统林业伐倒木的材积测算过程中通常将树干按长短以0.50或1.00 m进行分段相一致［25］。

LIANG等［11］和 SAARINEN等［26］在对高大通直的杉木材积研究中的干图像反映：立木干曲线虽然随着树高的增加总体呈减小趋势，但仍存在大量比上一级分段截面干径要大的情况，即不同的干径提取间隔会对立木材积测算造成一定影响。本研究通过以0.10 m区分段长度测算的立木材积为真值，对比分析各区分段下材积测算误差曲线图，发现随区分段长度的增加材积测算的平均误差及误差的离散度也会随之增加，主要是因为随着区分段长度的增加就会忽略越多的树干形变现象，而该现象在区分段长度由0.40 m增加0.50 m时尤其明显。这表明当区分段长度大于0.40 m时，测算的立木材积与真值之间的差距会明显增大，这也为TLS在如何精细高效分段测算材积提供了重要补充。

对比分析4种不同方法测算的立木材积，发现利用现有二元或一元材积模型测算的材积在总体上都要显著高于TLS区分求积值，并且测算的材积精度随立木胸径的增大的生长降低。这说明城市绿化树种干形与野外林分相比存在明显差异，而且随林龄的增大，其干形差异逐步趋大，现有的材积模型并不能很好地与之相匹配。史琰［17］、嵇浩翔等［27］也发现城市中复杂的环境条件、频繁的人为干扰，在不同程度上促进或抑制着立木的生长，使其生长态势相比野外林分存在极大的不确定性，如树干起始分叉位置的复杂多变，并且这种现象会随立木的不断生长而累积，与本研究结果具有一致性。

此外，本研究对5种不同CS测算方法的分析研究表明：基于一元材积模型测算CS会产生严重高估，主要是由测算立木材积过程中仅用胸径单一因子无法得到精确的材积数据导致的，因此，不建议利用一元材积模型测算城市绿化树种的立木材积及碳储量；基于二元材积模型以及树干碳储量模型测算的CS与以1.00 m为区分段长度测算的CS无显著差异，但相比以0.10 m为区分段长度测算的CS均显著偏高，说明两者作为常用的树干碳储量测算模型仅能对城市绿化树种树干碳储量进行粗略的测算，但与真实值存在一定的差距。该问题可能主要是由两大原因所引起，其一是由于存在材积测算误差，其二则是由于不同树种的树干单位体积碳储量存在差异，甚至相同树种不同径阶之间的树干单位体积碳储量也存在微小的差异，而现有的碳储量模型为保证广泛通用性大多采用多种阔叶树的均值来拟合构建。此外，不同碳储量测算方法间的显著性差异与材积间的显著性差异并非一致也说明CS是由材积及树干单位体积碳储量共同决定的。

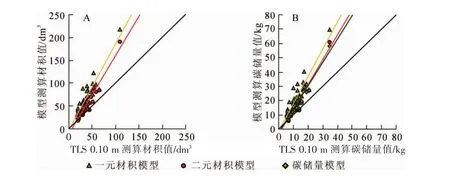
图4 现有模型测算的城市绿化树种材积及树干碳储量与TLS测算结果的比较Figure 4 Comparison of the urban greening tree species volume and stem carbon storage measured based on existing model

3.2 结论

基于TLS提取的胸径、树高能达到极高的精度。通过对比分析30株无患子基于TLS胸径和树高与外业实测值，其平均相对误差分别仅为1.97%和4.85%。表明基于TLS材积的单立木点云数据具有较高的还原度和客观真实等特点，也表明基于TLS提取的基本测树因子可在无需伐倒立木的情况下精确测算立木的材积，并结合树干钻芯取样，在对立木的正常生长不造成影响的前提下精确地测算树干碳储量。

不同的区分段长度对基于TLS测算的树干材积结果虽无显著影响，但随着区分段长度的增加，材积的测算精度仍会不断下降。因此，在对树干材积精度有较高要求的研究中，建议利用≤0.40 m的区分段长度进行树干材积的测算。该结论同样适用于伐倒木的材积精确测算。

城市绿化树种的主干材积及碳储量受环境因子和人为干扰影响与野外林分相比较存在显著差异。现有材积模型及碳储量模型仅能用于粗略测算城市绿化树种的材积及树干碳储量，但并不能到达高度匹配，尤其是一元材积模型。