基于最优误差动力学的时间角度控制制导律
李斌,林德福,何绍溟,白冰
1. 北京理工大学 宇航学院,北京 100081 2. 北京理工大学 无人机自主控制技术北京市重点实验室,北京 100081 3. 北京宇航系统工程研究所,北京 100076
现代战争中,机场和军舰等战略战术目标都采取多种防御措施来应对来袭导弹,比如面对空空导弹系统,电子干扰系统,近防武器系统[1]。协同攻击可以有效地应对上述防御措施对导弹的威胁[2]。多枚导弹在协同攻击目标时,为了取得更佳的毁伤效果,还希望以不同的终端攻击角度命中目标[3]。因此,本文研究了一种基于最优误差动力学的时间角度控制制导律,可以同时满足攻击时间和终端攻击角度的约束。
随着多飞行器协同控制问题的发展,带有攻击时间约束的制导问题在近几年被广泛研究[4]。文献[2]提出了一种基于传统比例导引的攻击时间控制制导律来实现协同攻击的任务。文献[5-6]提出了基于领弹和从弹的协同制导,从弹通过跟踪领弹来实现主从协同。文献[7]引入剩余飞行时间变量,提出了协同比例导引制导律,它通过减少各枚导弹剩余飞行时间之间的偏差来实现同时击中目标。文献[8]利用一种双层的控制结构,提出基于协调变量的时间协同制导律。文献[9]用多项式函数推导含时间控制的制导指令,附加导引头视场角限制的偏置项,设计了带视场角限制的攻击时间控制制导律。文献[10]研究了不需要剩余飞行时间的两段式制导策略,当导弹状态趋于一致后,切换成相同的比例导引制导律来实现协同攻击。
针对具有终端攻击角度约束的制导律研究已有很多,例如最优制导律[11-13],偏置比例导引律[14-15],非线性控制制导律[16-17]。文献[11-12]选取剩余飞行时间的函数为性能指标的权函数,基于二次型最优控制理论推导了带终端角度约束的制导律。文献[13]针对带有终端角度约束的任意函数加权最优制导问题,应用Schwarz不等式求解了有无控制系统动力学情况下最优制导律的一般表达式。文献[14-15]研究了无剩余飞行时间的偏置制导律,在比例导引律的基础上附加角度约束偏置项,利用改变过载指令控制终端攻击角度。文献[16]基于连续二阶滑模理论设计了有限时间收敛的角度约束制导律,具有很强的鲁棒性。文献[17]将终端攻击角度约束转化为终端视线角约束,利用螺旋控制算法设计了一种二阶滑模变结构制导律。
同时考虑攻击时间和终端攻击角度的制导律也有一些研究。通过对文献[2]的拓展,文献[18]提出了攻击时间和角度控制制导律,可以同时满足攻击时间和终端攻击角度的约束。文献[19]选择满足攻击时间和终端攻击角度约束的滑模面,基于二阶滑模理论和最优控制理论设计了攻击时间和角度控制制导律。文献[20]在偏置比例导引律基础上附加攻击时间误差反馈项,实现了期望的攻击时间和终端攻击角度。文献[21]研究了带有攻击时间和攻击角度控制的三维制导问题,基于Lyapunov稳定性理论和时间误差补偿设计了带攻击时间和攻击角度控制的三维制导律。
制导律的设计可以转化为一种有限时间跟踪问题,目的是希望在有限时间内将跟踪误差调整为零。根据不同的制导目的,跟踪误差可选择为零控脱靶量,视线角速率,攻击时间误差,攻击角度误差等[22]。以往研究的误差动力学只是将跟踪误差收敛到零,未考虑跟踪误差的收敛模式,一些基于非线性控制方法的时间角度控制制导律设计没有明确的性能指标。本文研究了跟踪误差的最优收敛模式,给出了实现跟踪误差最优收敛模式的最优误差动力学,考虑攻击时间和终端攻击角度约束,设计了基于最优误差动力学的时间角度控制制导律,并给出了相应的性能指标,得到的是一种能量最优形式的制导律,且制导律中各部分制导指令的物理意义明确。最后,对不同参数情况下进行仿真,结果表明设计的制导律实现了期望的攻击时间和终端攻击角度。
1 问题描述
建立弹目相对运动的数学模型,图1为导弹攻击固定目标的二维平面示意图。其中VM为导弹速度,aM为制导指令,R为导弹和目标的相对
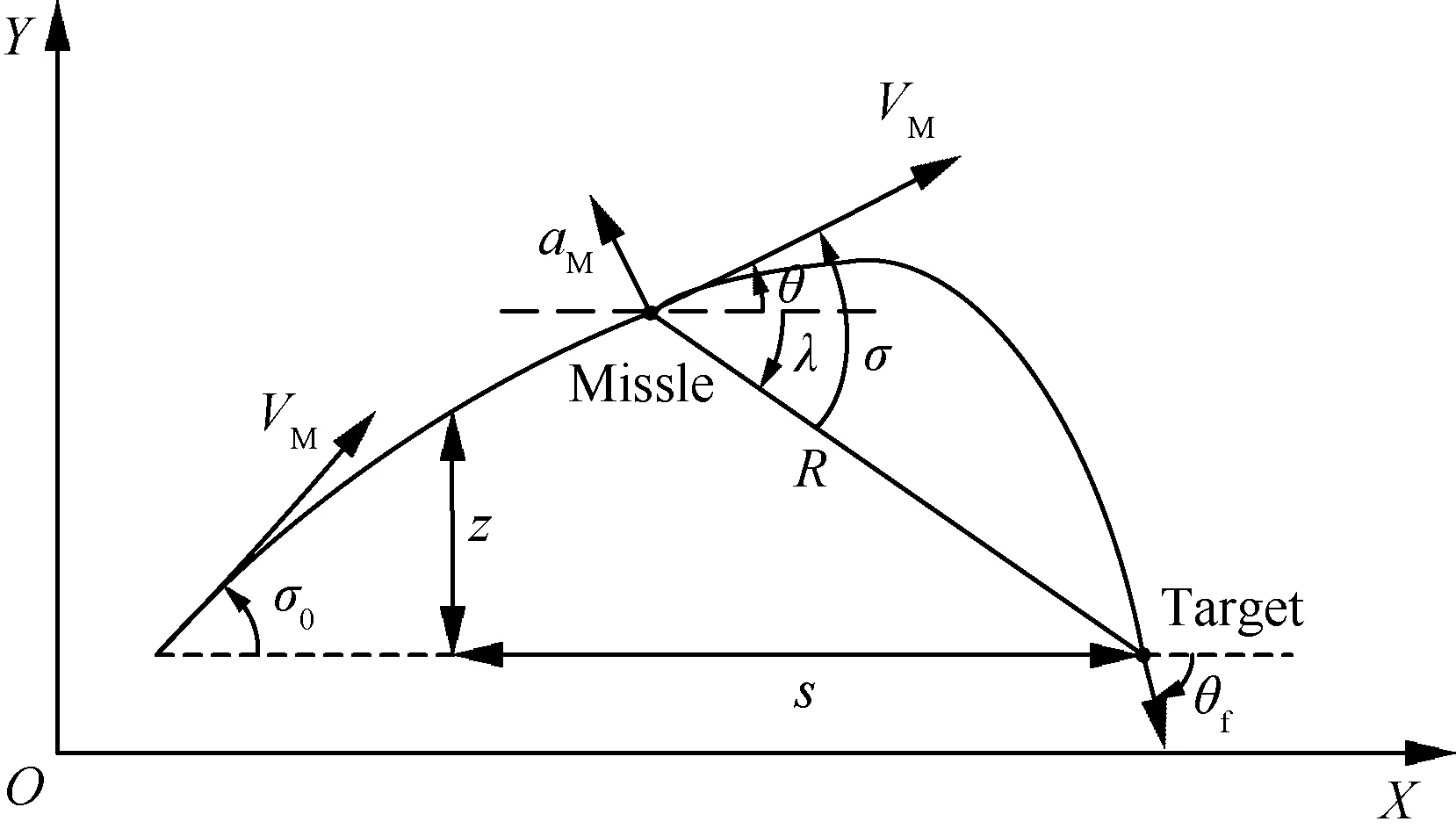
图1 导弹与目标运动关系Fig.1 Relationship of missile-target engagement
距离,λ、θ和σ分别为弹目视线角、导弹速度方向角和速度方向误差角,σ0为初始速度方向误差角。z和s分别为弹目视线系下表示距离的参数。
弹目相对运动方程为
(1)
导弹的运动学方程为
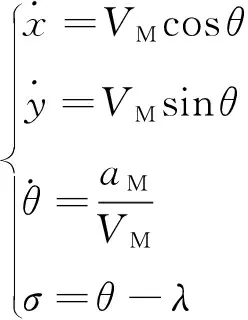
(2)
初始和终端约束分别为
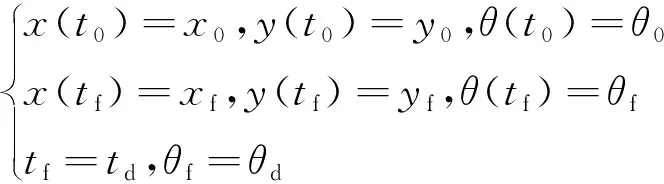
(3)
式中:(x0,y0)和(xf,yf)分别为导弹的初始位置和目标位置;t0和tf分别为初始和终止时刻;θ0和θf分别为导弹的初始速度方向角和终端攻击角度;td为期望的攻击时间;θd为期望的终端攻击角度。
2 最优误差动力学
跟踪问题的系统方程一般表示为
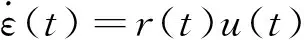
(4)
式中:ε(t)为跟踪误差;r(t)为已知的时变函数;u(t)为控制输入。
首先选择一个期望的误差动力学,然后计算在期望的误差动力学下满足系统方程式(4)的控制输入。根据不同的制导目的,跟踪误差可选择为零控脱靶量,视线角速率,攻击时间误差,攻击角度误差等,r(t)与选取的跟踪误差有关,因为上述跟踪问题都是可控的,所以r(t)是可逆的,有r(t)≠0。
制导律设计中一种传统的期望误差动力学为
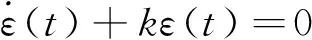
(5)
式中:k>0为控制跟踪误差收敛速度的比例增益。
解式(5)可得跟踪误差的解析式为
ε(t)=ε(t0)e-kt
(6)
式中:ε(t0)为初始跟踪误差。
式(6)表明跟踪误差按指数函数形式渐进地收敛到零,收敛速度与比例增益k有关。这种期望的误差动力学只是将跟踪误差收敛到零,没有考虑如何选取明确的性能指标最优地实现零跟踪误差。
考虑跟踪误差的最优收敛模式,利用Schwarz不等式推导最优误差动力学[22]。
期望的误差动力学选取为
(7)
式中:tgo为剩余飞行时间;
(8)
其中:H(t)>0为权函数。
性能指标为
(9)
实现期望的误差动力学式(7)并使性能指标式(9)取最小值需要的控制输入为

(10)
证明过程可参考文献[22]。
误差动力学式(7)的形式即为最优误差动力学,它保证了设计的制导律在有限时间内收敛,因为它是直接求解有限时间最优跟踪问题得到的。
对最优误差动力学特性进行分析,传统期望误差动力学与最优误差动力学为
(11)
对比式(11)的两种误差动力学,可知传统期望误差动力学与最优误差动力学的区别在于比例增益不同。传统期望误差动力学的比例增益是一常值k,最优误差动力学的比例增益是时变值φ(t)/tgo。
分析最优误差动力学的时变比例增益,由于
(12)
随着剩余飞行时间趋于零,最优误差动力学的时变比例增益由一个初始小值增大到无穷大,时变比例增益的变化形式与φ(t)有关。
令Γ(t)=H-1(t)r2(t),可将φ(t)写为
(13)
函数r(t)与具体的制导问题有关,权函数H(t)是设计参数,根据不同的目标选取合适的权函数H(t)。
分析式(13)可得,对于给定的r(t)和H(t),始终有φ(t)>0。当Γ(t)为常数时,φ(t)=1;当Γ(t)随着t→tf减小时,φ(t)>1;当Γ(t)随着t→tf增大时,φ(t)<1。
下面分析两种情况。
1)当r(t)是时不变函数,权函数H(t)=1时,φ(t)为
(14)
最优误差动力学使性能指标式(15)取最小值得到的是控制量平方积分最小的制导律。
(15)
(16)
这种情况下,φ(t)=K为一常数。
期望误差动力学使下述性能指标式(17)最小。
(17)
当r(t)=1且K=1时,性能指标式(17)退化为性能指标式(15)。
最优误差动力学为
(18)
解式(18)可得最优跟踪误差的解析式为
(19)
这种最优误差动力学在实际中是可用的,因为跟踪误差的收敛模式作为剩余飞行时间的函数是可预测的,并且最优误差动力学由简单形式给出,这种最优误差动力学可应用于各种类型的制导问题。
3 时间角度控制制导律
本节利用最优误差动力学方法设计时间角度控制制导律,在广义最优角度制导律的基础上增加攻击时间误差反馈项,将攻击时间误差看做跟踪误差,设计的制导律使跟踪误差以最优模式在有限时间内收敛到零,最终实现攻击时间和终端攻击角度的共同控制。
3.1 广义最优角度控制律的剩余飞行时间
广义最优角度制导律可表示为[12]
(20)
式中:n=0,1,2,…;σf=θf-λ。
在对广义最优角度控制律进行剩余攻击时间估算时,不仅要考虑比例导引过载指令对弹道曲率的影响,还要考虑用于终端攻击角度控制的过载指令对弹道的影响。
定义z为关于沿弹目视线参数s的多项式函数
z=an+3sn+3+an+2sn+2+…+a1s+a0
n=0,1,2,…
(21)
根据小角度假设,速度方向误差角表示为
σ=-[(n+3)an+3sn+2+(n+2)
an+2sn+1+…+a1]
n=0,1,2,…
(22)
根据边界条件
(23)
当n≥1时,补充方程

(24)
将式(23)和式(24)代入式(21)和式(22),可解出待定系数为
(25)
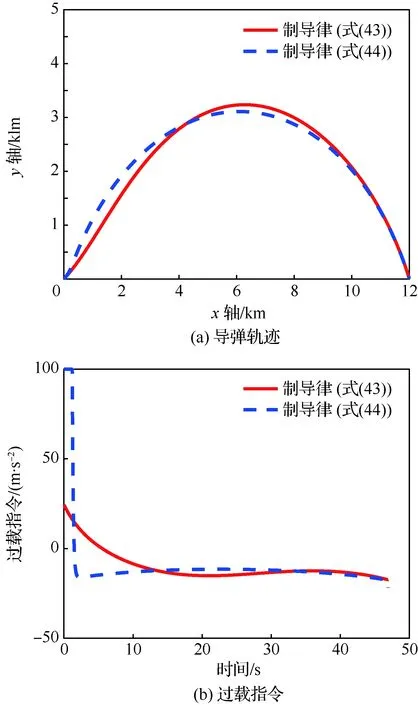
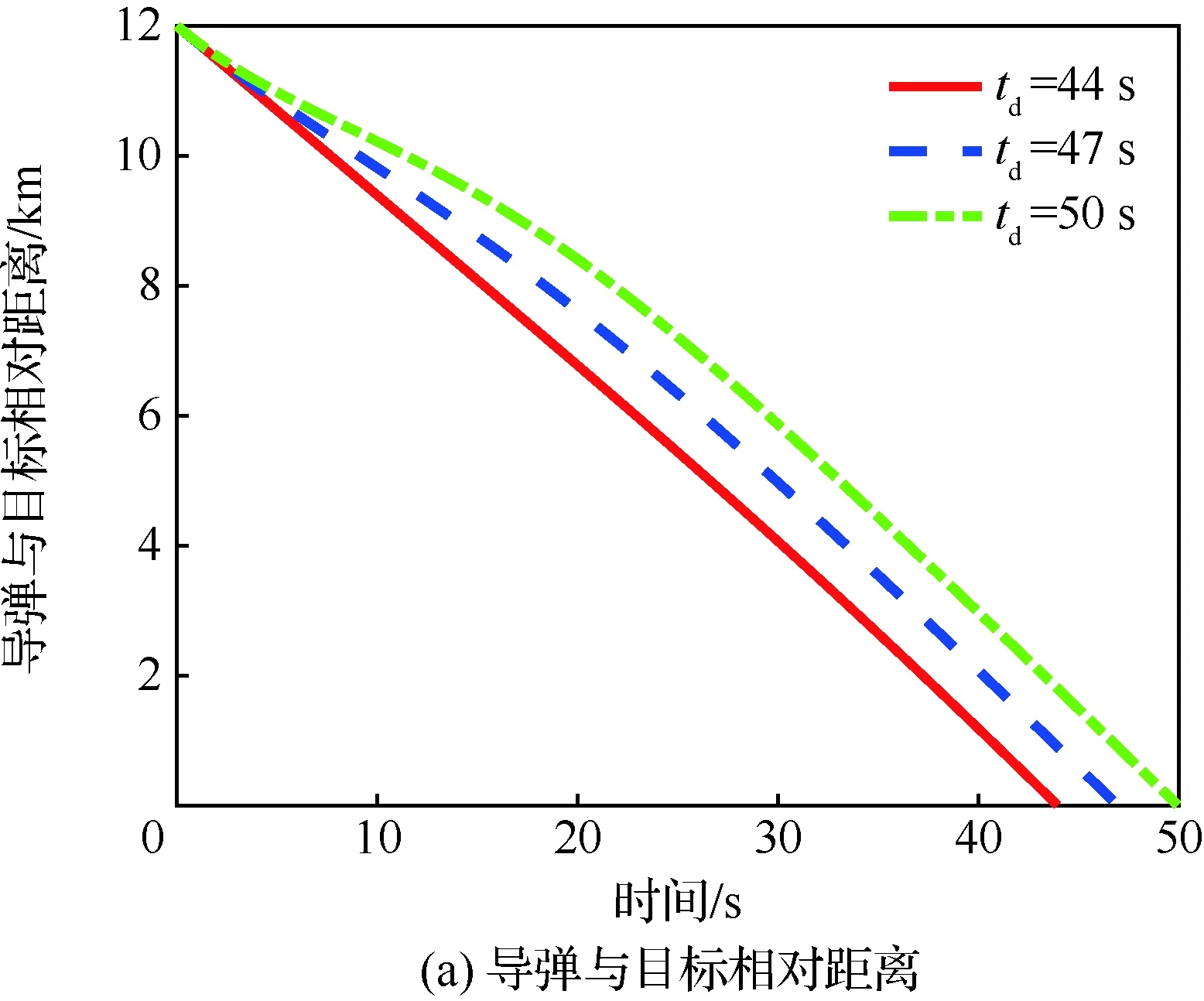
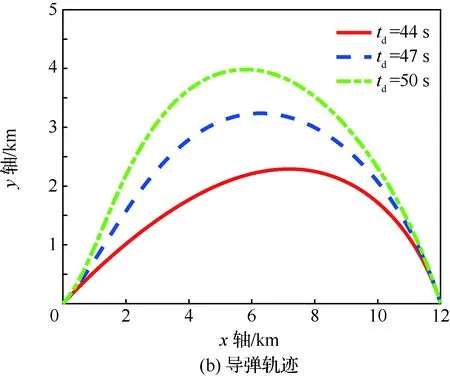
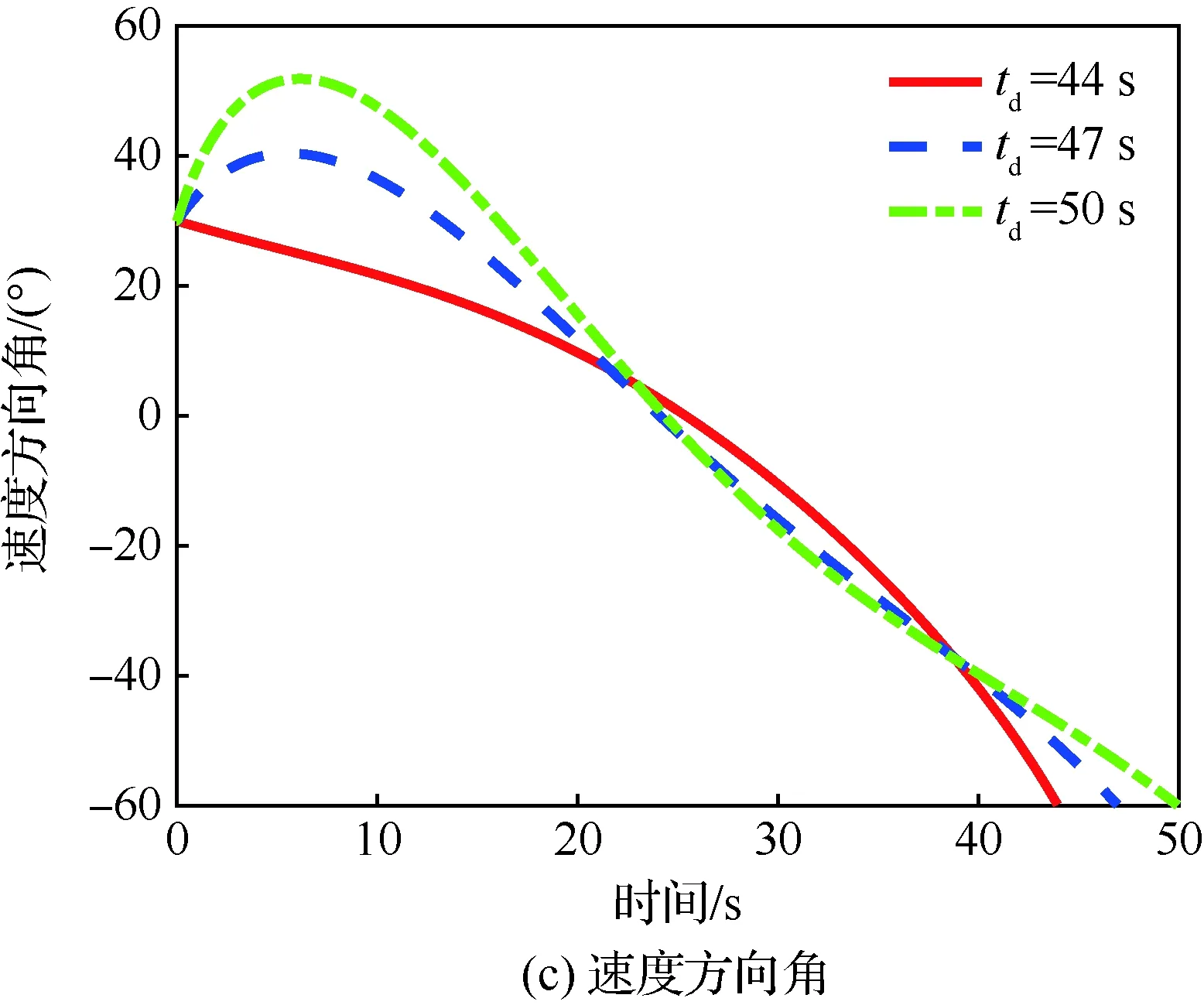
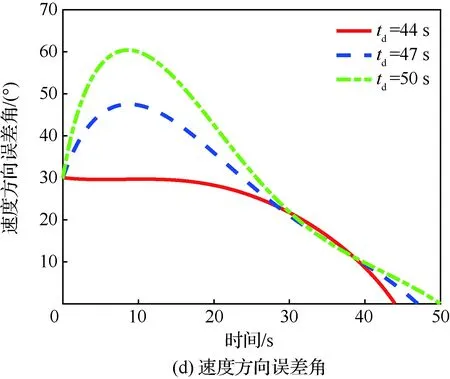
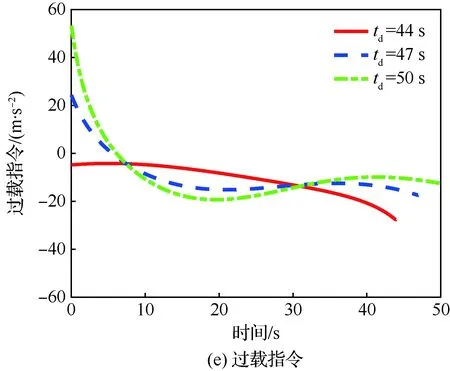
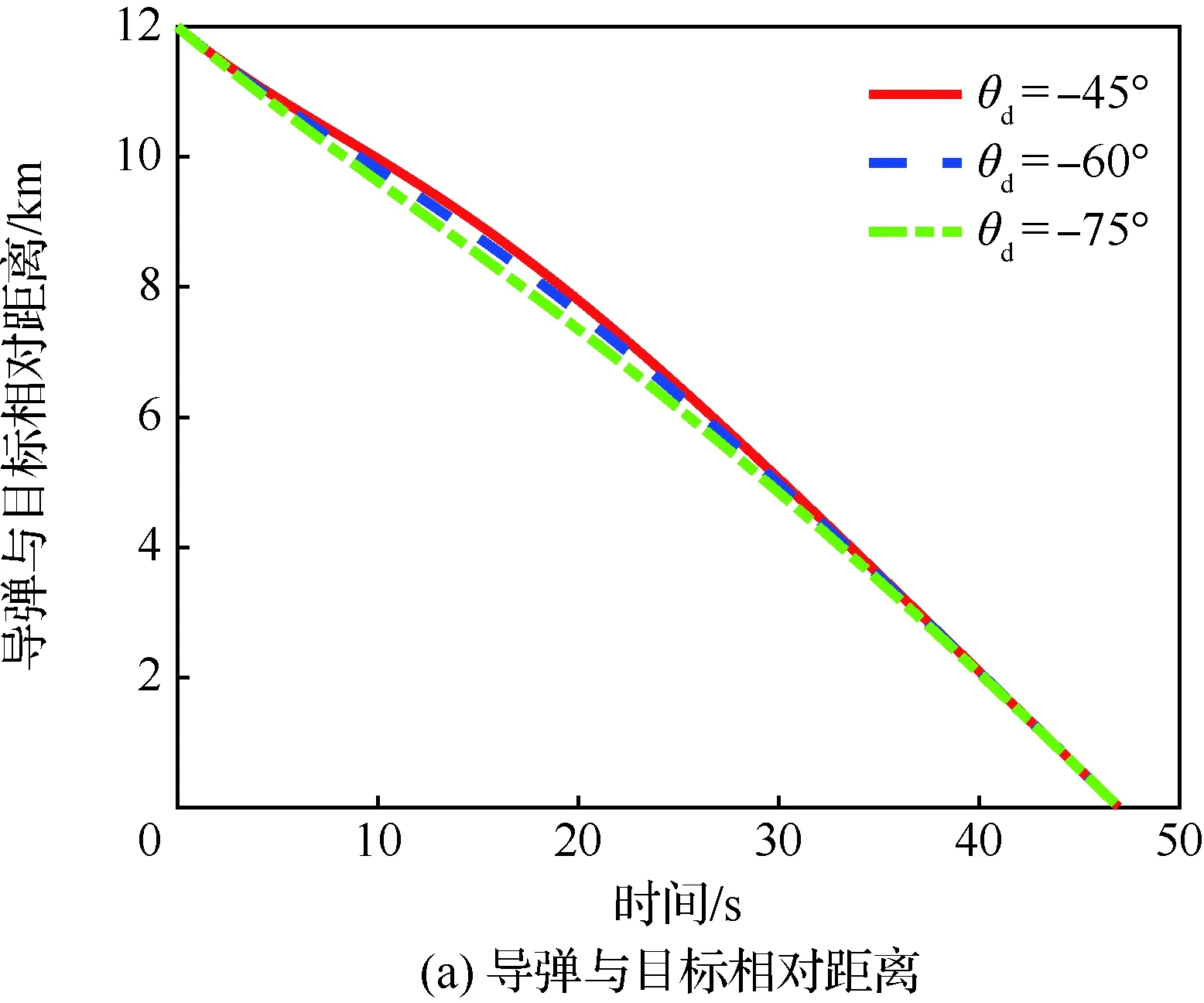
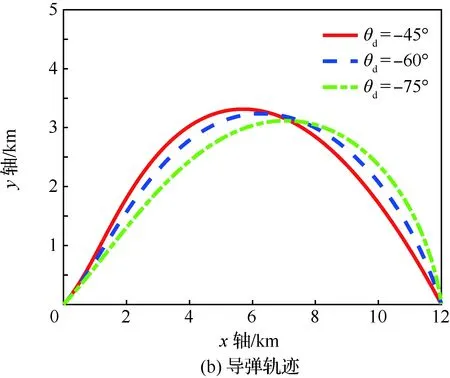
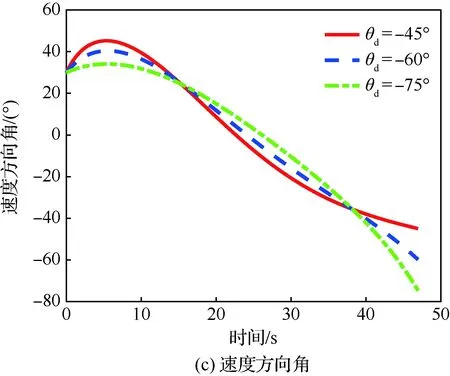
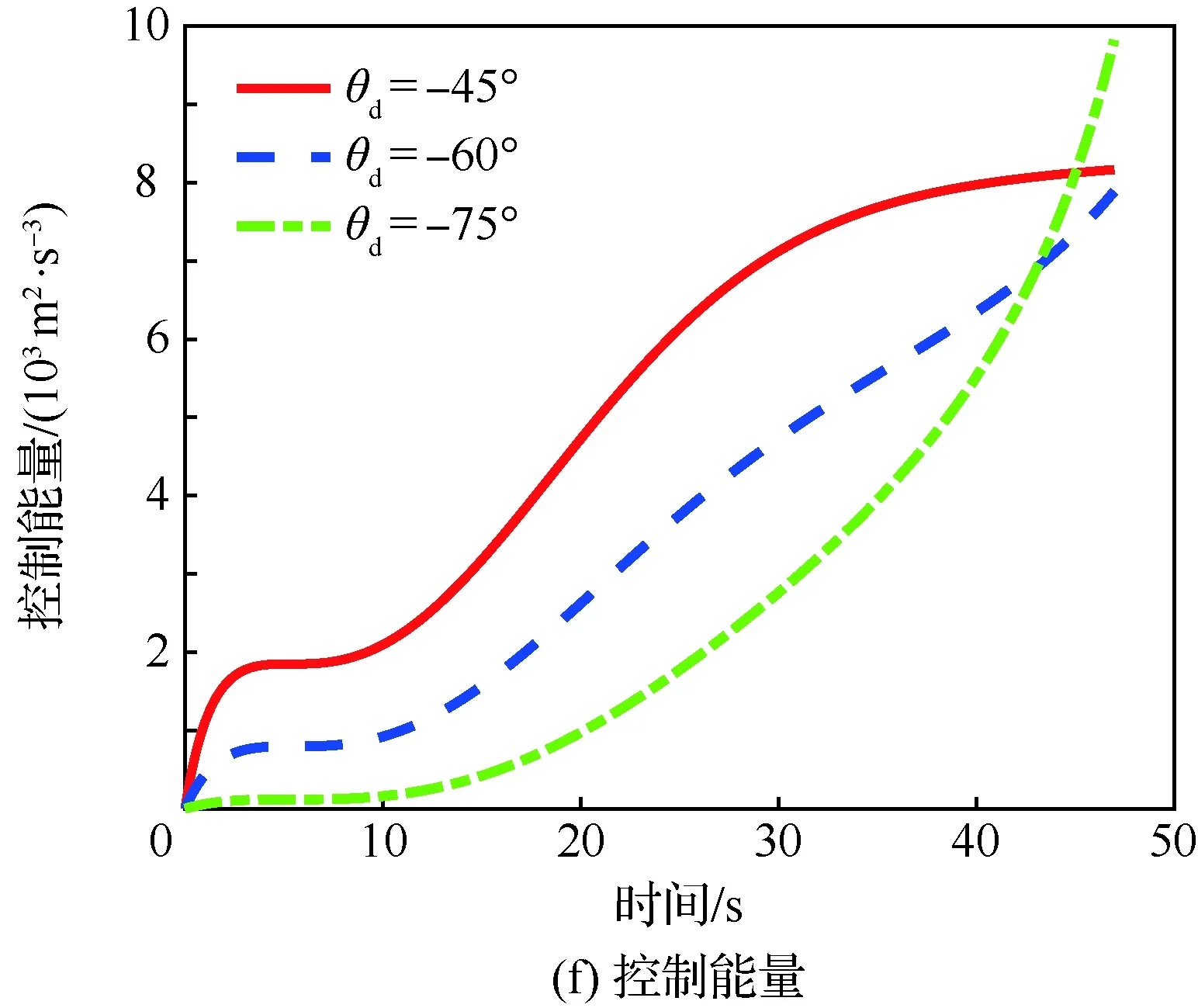
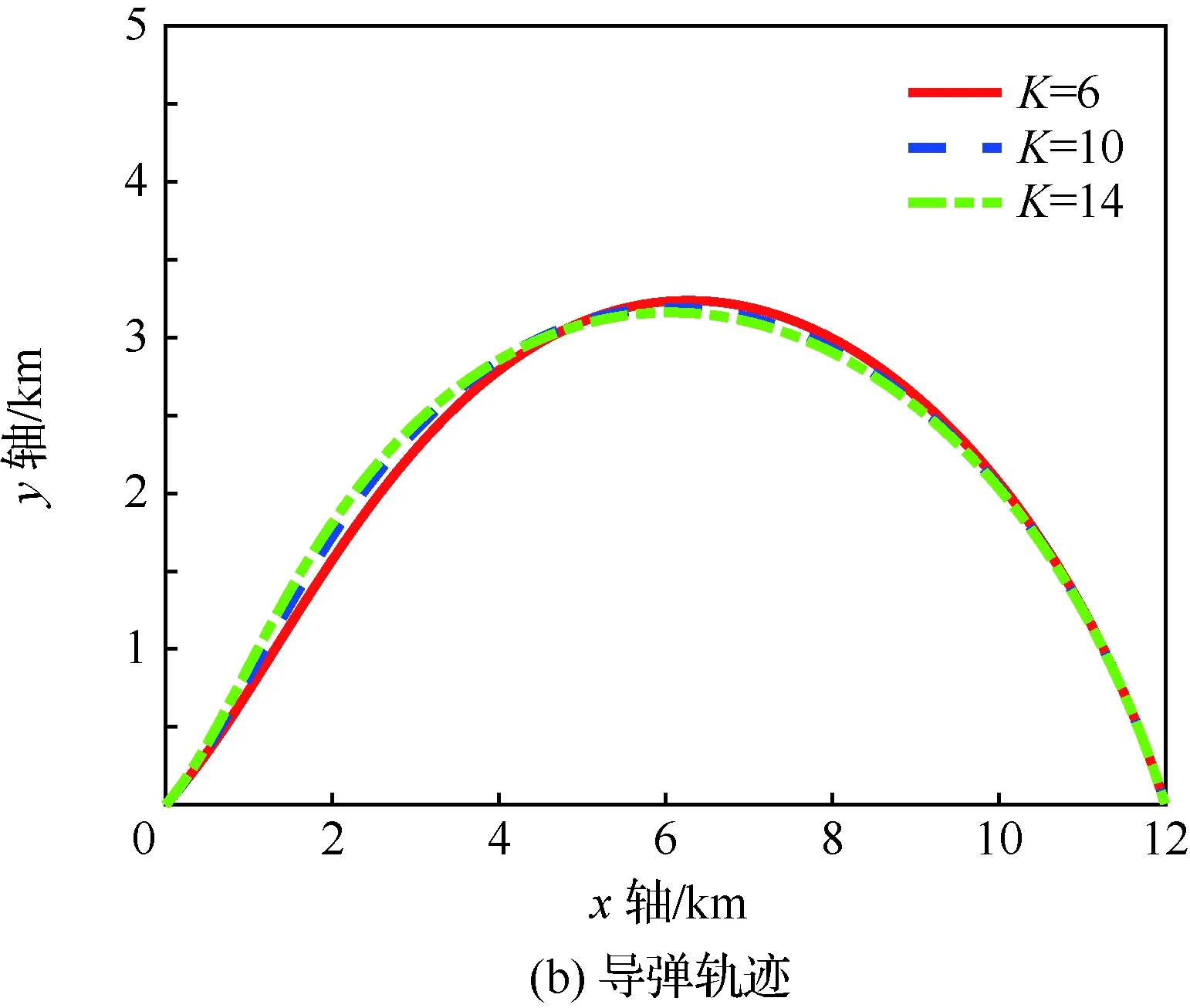
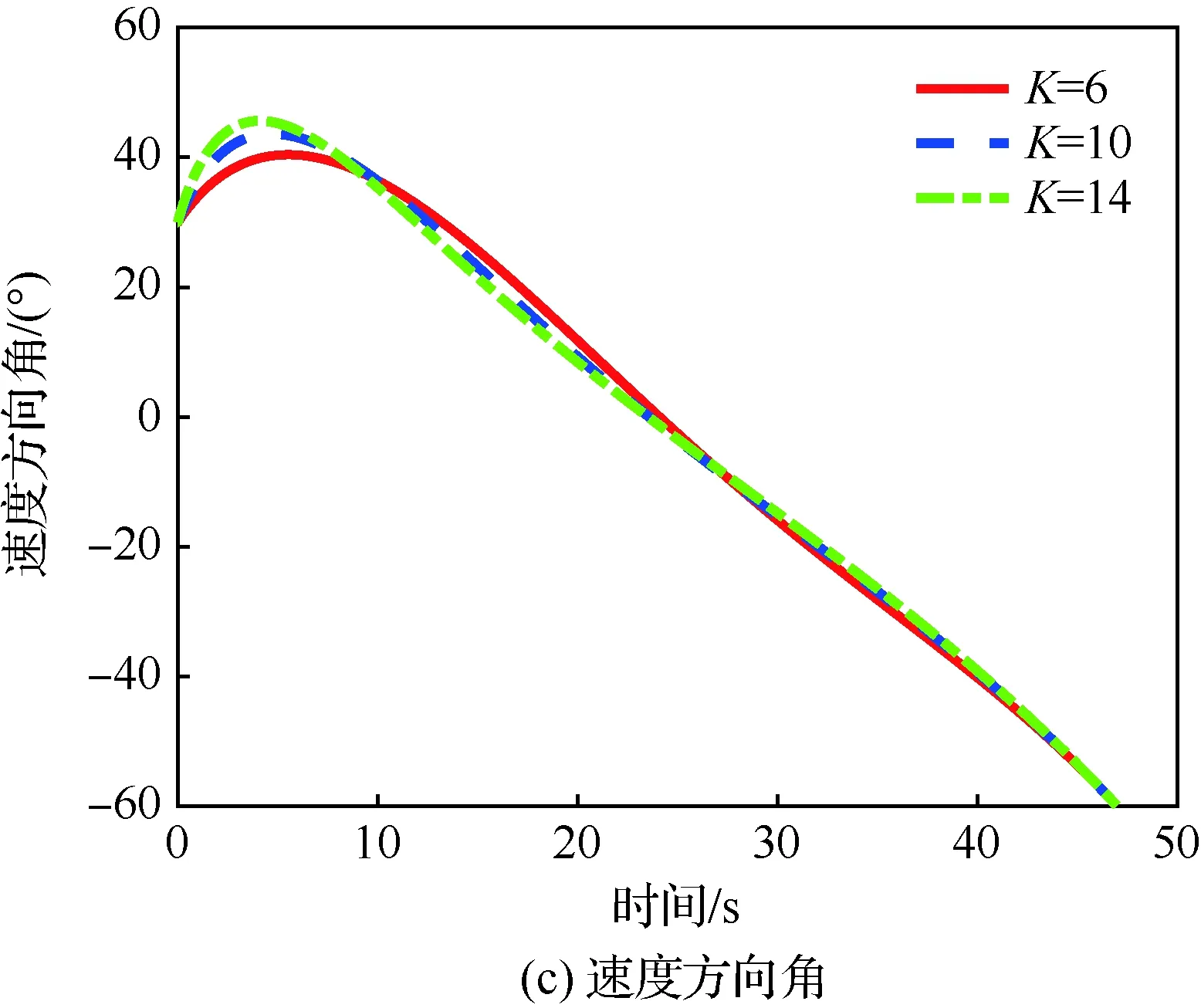
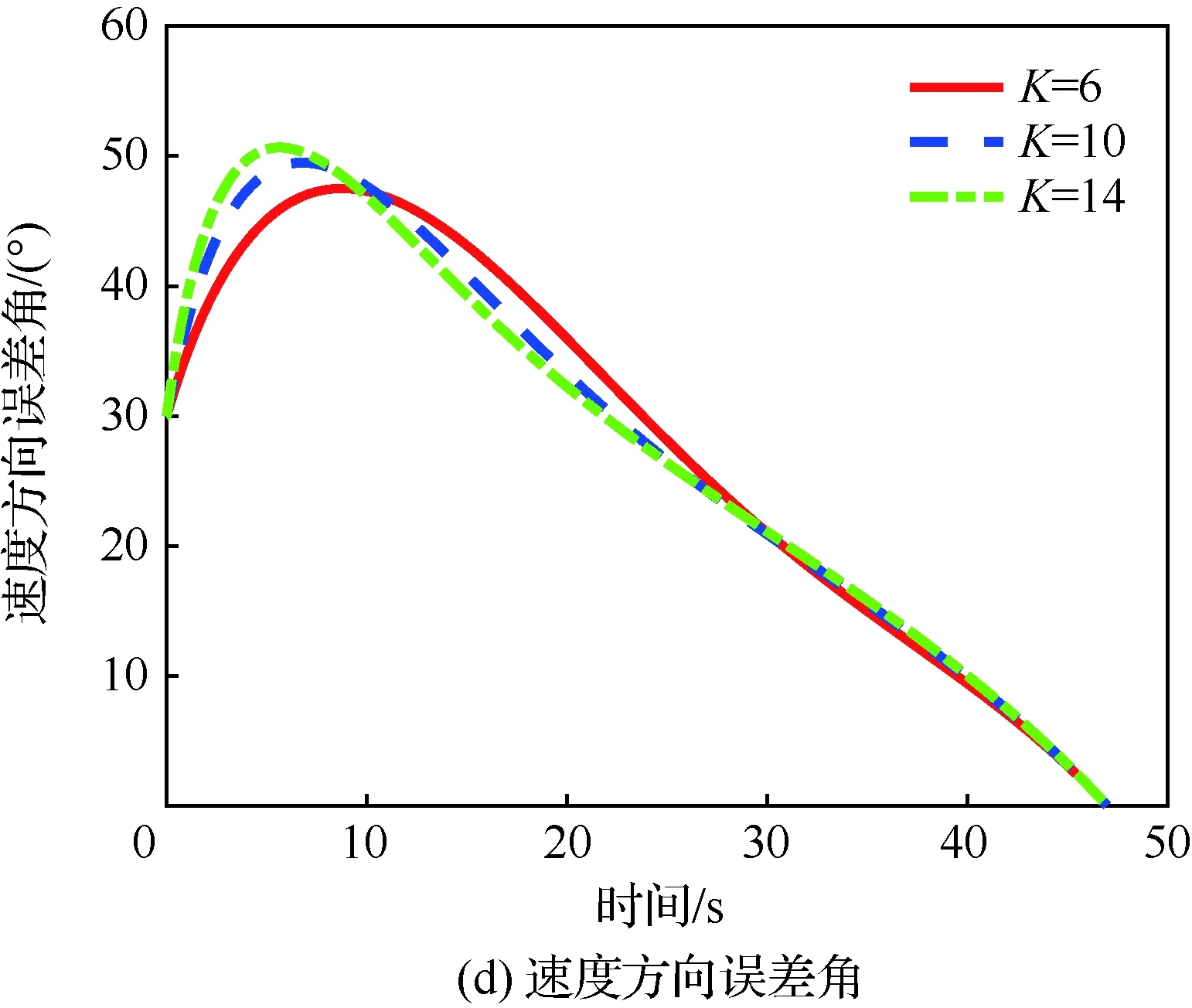
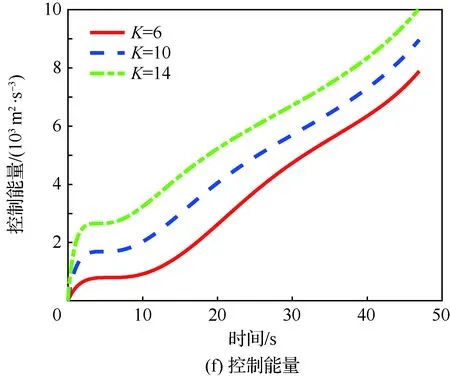
当1 考虑终端攻击角度约束的剩余飞行时间估计表示为 (26) 式中:Δ为由于弹道弯曲增加的剩余飞行时间的比例。 将式(21)对s求导可得 (27) 利用泰勒公式并略去高阶项有 (28) 将式(28)代入式(27)得 (29) 时间角度控制制导律的制导指令表示为 aM=aOA+aIT (30) 式中:aIT为攻击时间误差反馈项制导指令。 3)σ+(2n2+6n+3)σf]sinσ (31) 将上述简化关系代入式(31)并且忽略高阶项得 [(2n+3)σ+(2n2+6n+3)σf]σ= (n+1)σf]aIT (32) 攻击时间误差定义为 εt=td-tf (33) 将攻击时间误差εt看作跟踪误差,利用第2节的方法,可得 [(2n+4)σ-(n+1)σf]aIT (34) 攻击时间控制问题的时变函数r(t)和控制输入u(t)分别为 (35) 关于攻击时间误差εt的最优误差动力学 (36) 性能指标为 (37) 将式(36)代入式(34)得 (38) 则时间角度控制制导律为 (39) 式(39)也可表示为 (40) 可以看出,时间角度控制制导律包含比例导引项,终端攻击角度控制项和攻击时间误差反馈控制项。其中比例导引项保证命中目标,终端攻击角度控制项和攻击时间误差反馈控制项使导弹分别满足期望的终端攻击角度和期望攻击时间。当攻击时间与期望的攻击时间实现一致后,攻击时间误差反馈控制项的制导指令收敛为零,时间角度控制制导律退化为广义最优角度制导律。 当n=0时,广义最优角度制导律即弹道成型制导律,时间角度控制制导律为 (41) 性能指标为 (42) 以时间角度控制制导律式(41)为例,仿真验证在不同参数条件下的性能。式(41)可表示为 (43) 不考虑跟踪误差的收敛模式,由传统的误差动力学式(5)得到的时间角度控制制导律为 (44) 可以看出制导律中的设计参数为期望攻击时间td、期望终端攻击角度θd和制导增益K,不同的参数不仅可以改变导弹的弹道轨迹,也会影响对控制能量的消耗。 控制能量定义为 (45) 导弹初始位置(0,0) m,目标位置(12 000,0) m,初始速度方向误差角σ0=30°,导弹速度VM=300 m/s,导弹最大可用过载amax=10g。 首先对比基于最优和传统误差动力学的时间角度控制制导律式(43)、式(44)的性能。选取期望的攻击时间为47 s,终端攻击角度θd=-60°,制导增益K=6。 图2给出了不同跟踪误差收敛模式下的弹道、过载指令和控制能量曲线。仿真结果表明,制导律式(43)、式(44)都实现了期望的攻击时间和终端攻击角度,但不考虑跟踪误差收敛模式的制导律式(44)需要很大的初始过载和更多的控制能量,并且没有明确的性能指标。 下面分别分析td、θd和K对基于最优误差动力学的时间角度控制制导律式(43)性能的影响。 图2 不同跟踪误差收敛模式下的仿真结果Fig.2 Simulation results of different tracking error convergence patterns 研究不同攻击时间情况下的性能。选取期望的攻击时间分别为44、47、50 s,终端攻击角度θd=-60°,制导增益K=6。 图3给出了不同攻击时间下的导弹与目标相对距离、弹道、速度方向角、速度方向误差角、过载指令和控制能量曲线。由图3(a)和图3(c)可看出,在时间角度控制制导律作用下,实现了不同攻击时间和期望的终端攻击角度约束。在比例导引制导律作用下的飞行时间tf=40.8 s,终端攻击角度θf=-10°,越大的期望攻击时间要求弹道越弯曲,因此在初始段导弹以速度方向误差角增大的方向飞行来增加弹道长度。仿真结果图3(d)~图3(f)表明,攻击时间和角度的跟踪误差越大,初始段速度方向误差角增加越多,需要的过载越大,控制能量消耗越多。 图3 不同攻击时间下的仿真结果Fig.3 Simulation results of different impact time 分析不同终端攻击角度情况下的性能。选取期望的终端攻击角度分别为-45°,-60°,-75°,攻击时间td=47 s,制导增益K=6。仿真结果如图4所示。 图4(a)和图4(c)分别为弹目相对距离曲线和速度方向角曲线,导弹以期望的终端攻击角度在攻击时间47 s命中目标。在弹道成型制导律作用下,实现-45°,-60°,-75°终端攻击角度的飞行时间分别为43.04、44.57、46.52 s。图4(d)~图4(f)表明,终端攻击角度-45°的时间误差最大,为了增加攻击时间,初始段需要以速度方向误差角增大的方向飞行,相应的需要较大过载和控制能量。终端攻击角度-75°的攻击时间误差较小,初始段需要较小的过载和控制能量,在弹道末端需要较大的过载和控制能量来实现大的终端攻击角度。终端攻击角度-60°时消耗的控制能量最小,因此在选择制导律参数时,需要权衡攻击时间和终端攻击角度的匹配问题。 图4 不同终端攻击角度下的仿真结果Fig.4 Simulation results of different terminal impact angles 图5仿真对比了不同制导增益K下的时间角度控制制导律性能。选取攻击时间td=47 s,终端攻击角度θd=-60°,制导增益K分别为6、10和14。仿真结果表明,制导增益K越大,攻击时间误差收敛越快,但需要更大的过载和控制能量。由图5(a)和图5(c)可看出,不同的制导增益K都实现了期望的攻击时间和终端攻击角度。 图5 不同制导增益下的仿真结果Fig.5 Simulation results of different guidance gains 1) 本文考虑攻击时间和终端攻击角度约束,提出了一种时间角度控制制导律,该制导律由广义最优角度控制制导律和攻击时间误差反馈项组成,分别用来进行终端攻击角度控制和攻击时间控制。 2) 考虑跟踪误差的最优收敛模式,利用Schwarz不等式推导了最优误差动力学,给出了广义最优角度控制制导律作用下的剩余飞行时间估算表达式,将攻击时间误差看作跟踪误差,设计基于最优误差动力学的时间角度控制制导律,实现了攻击时间和终端攻击角度的共同控制。 3) 该制导律形式简单,仿真表明在不同的设计参数下均有较好的性能,具有良好的工程应用价值。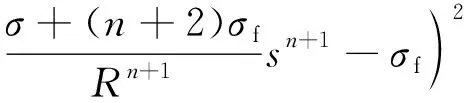
3.2 制导律设计

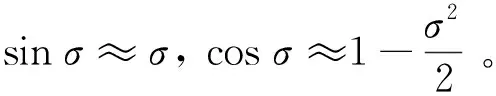
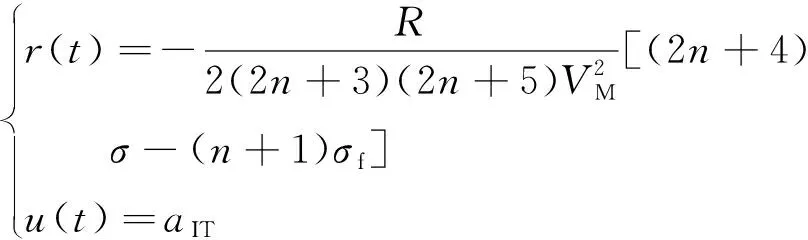
4 仿真分析

4.1 不同攻击时间

4.2 不同终端攻击角度


4.3 不同制导增益


5 结 论

