循环加载下复合推进剂的能量耗散

童心，陈雄，许进升,，杜红英，周长省

1. 南京理工大学 机械工程学院，南京 210094 2. 晋西工业集团有限责任公司 技术中心，太原 030027

以固体火箭发动机为动力的空空导弹在完整的寿命期内一般导弹要经历运输、贮存、挂载飞行、机动飞行和自主飞行等阶段，会遇到温度、湿度、振动、盐雾和霉菌等一系列自然和诱发环境。其中，挂载飞行阶段是空空导弹挂载在战斗机上执行任务的主要阶段，导弹弹体的振动频率可高达几千赫兹[1]。固体推进剂作为典型的黏弹性材料[2]，其循环应力-应变行为表现出明显的滞后性，在循环载荷作用下机械能会由于滞后效应以热能的形式耗散，但由于材料极低的导热系数[3]，使得热能无法在短时间内扩散到外界环境，因此材料内部和表面温度有明显的升高[4]。固体推进剂是温度敏感材料[5]，温度的急剧升高会极大地削弱其动态力学性能，进而影响发动机的内弹道性能。对经受振动的高填充比发动机而言，还会发生另一个问题：在振动期间，伴随能量耗散引起的温度升高会引起药柱的膨胀，甚至充满药柱的自由容积。如果不具备足够的自由容积，就有可能引起推进剂与推进剂、推进剂与壳体的接触，这种接触可能引起发动机局部温度的上升，导致因推进剂力学性能降低而引起的结构破坏[6]。此外，由于固体火箭发动机在制造、贮存、运输过程中受到温度、振动等环境因素的影响，在推进剂内部易于形成微小裂纹、微孔洞等损伤，能量耗散会加快损伤的演化过程。因此，研究循环加载下复合推进剂的能量耗散具有十分重要的理论和工程意义。

围绕固体火箭发动机在循环载荷下的响应，邢耀国等[7]通过实际观测和数值仿真研究了舰载导弹上固体火箭发动机的疲劳寿命及其影响因素；关于固体火箭发动机受环境因素的影响，高艳宾等[8]分析了NEPE(高能硝酸酯增塑聚醚)推进剂在不同载荷水平下的疲劳损伤，并构建非线性损伤模型获取了疲劳损伤的演化规律。然而，目前研究主要集中在循环力学性能和疲劳损伤方面，针对固体推进剂疲劳生热的宏观观测及温升预测报道较少[9]。实际上，材料的疲劳过程是一个复杂的能量耗散过程，包括弹性应变能[10]、塑性应变能[11]、黏弹性迟滞能[12]、热耗散[13]、储能[14]、声发射、电磁等。对于复合固体推进剂而言，非弹性应变能(塑性应变能、迟滞能等)的很大部分以热的形式耗散于环境中，引起材料自身温度升高[15-16]。以往关于推进剂疲劳的研究通常假定推进剂变形时的温度场与环境一致，这与循环载荷下推进剂变形伴随着温度升高的现象不符。

为深入研究复合推进剂在使用寿命中遭遇的能量耗散和滞后温升问题，进行了应变控制模式下的疲劳实验以获取循环应力-应变特性；同时为获取材料变形中的温度场，借助非接触式测温装置采集了推进剂试件疲劳变形时表面的实时温度，分析了影响温升的两个重要因素。随后建立物理模型和温度场方程得到了导热微分方程组，并利用有限元仿真对不同加载条件下推进剂的滞后温升进行了预测。

1 实验

1.1 材料和试件

研究对象为HTPB(Hydroxyl-Terminated PolyButadiene)三组元复合推进剂，各组元的质量分数为：铝粉(Al)17%，高氯酸铵(AP)70%，粘合剂HTPB橡胶及其他组分13%。HTPB推进剂的密度、比热容和导热系数等参数见表1。

表1 HTPB推进剂的参数Table 1 Parameters of HTPB propellant

1.2 实验装置与方法

初次实验时发现，HTPB推进剂较软，难以直接固定在实验设备的夹具上。为了改善夹持问题，消除不稳定加载或避免标距不精确，自行设计了与夹具适配的金属夹头(由45钢制成)。夹头和推进剂试件由两液混合硬化胶粘接固定，根据图1所示制备试件。在测试前，试样放在保温箱内保温24小时以消除推进剂内部的残余应力。

疲劳实验在动态热机械分析仪(Dynamic Mechanical Analyser，DMA，型号为美国BOSE公司的ELF3200)上进行。DMA主要由动磁式直线电机、温控箱、力传感器、位移传感器、数据采集系统等组成。该系统能实现精确的位移和力控制，其灵敏度分别为0.01 mm和0.01 N。DMA的工作频率范围为1×10-5～2×102Hz。利用FLIR-A615型红外热像仪对HTPB推进剂试件表面温度进行实时监测，红外热像仪的响应光谱范围为7.5～14 μm，空间分辨率达到640 pixel×480 pixel。热成像的采集频率为25 Hz，热分辨率在25 ℃时小于0.025 ℃，一般为0.02 ℃。实验装置如图2所示。

参考GB/T 26077—2010《金属材料疲劳轴向应变控制方法》，疲劳实验采用了应变控制模式，对试件加载对称正弦应变ε=εasin2πft，其中频率f为1、10、50、100 Hz；实验应变幅值εa=εmax-εmin/2为0.01、0.03、0.05，εmax为加载最大应变，εmin为加载最小应变；t为时间。实验前，所有试件标距表面都需喷涂上一层黑色亚光漆，以避免发射光的干扰，提高试件表面热辐射率。实验中采集了标距内的最高温度，下文出现的温度均指试件标距内的最高温度。

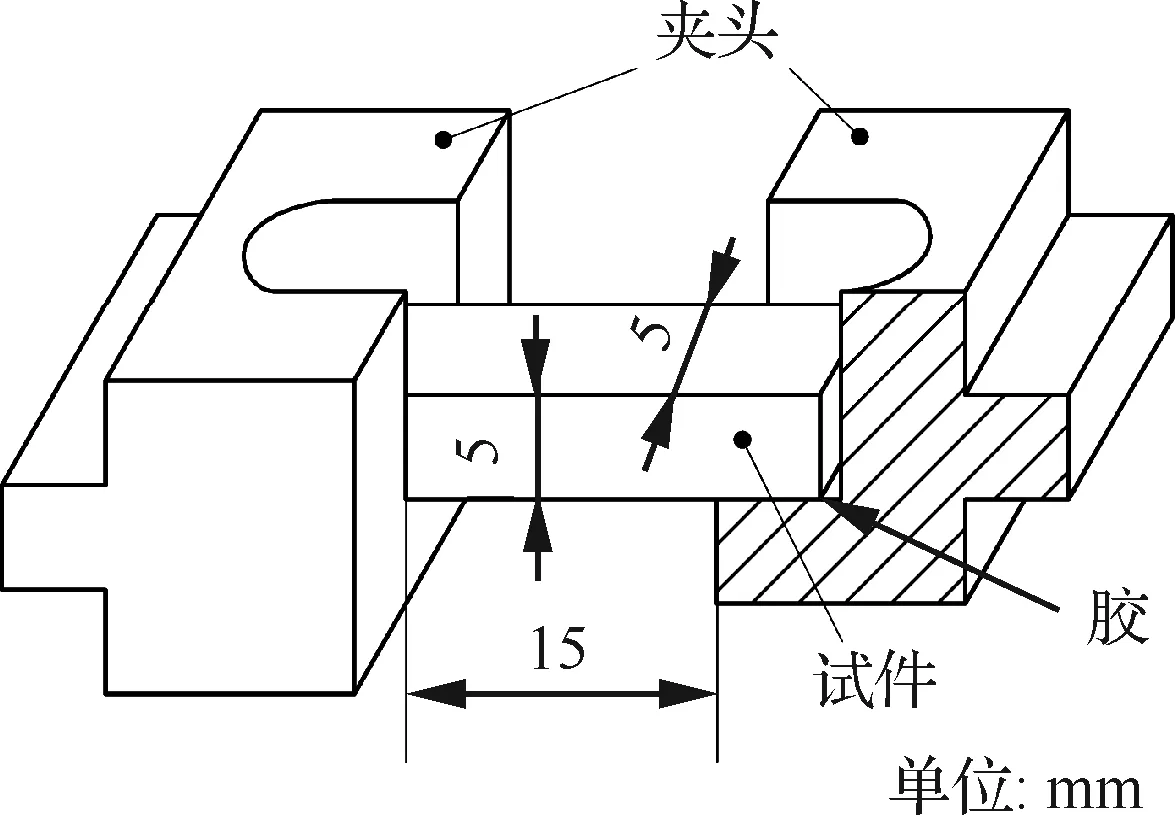
图1 HTPB推进剂试件的装夹Fig.1 Clamping of HTPB propellant specimen

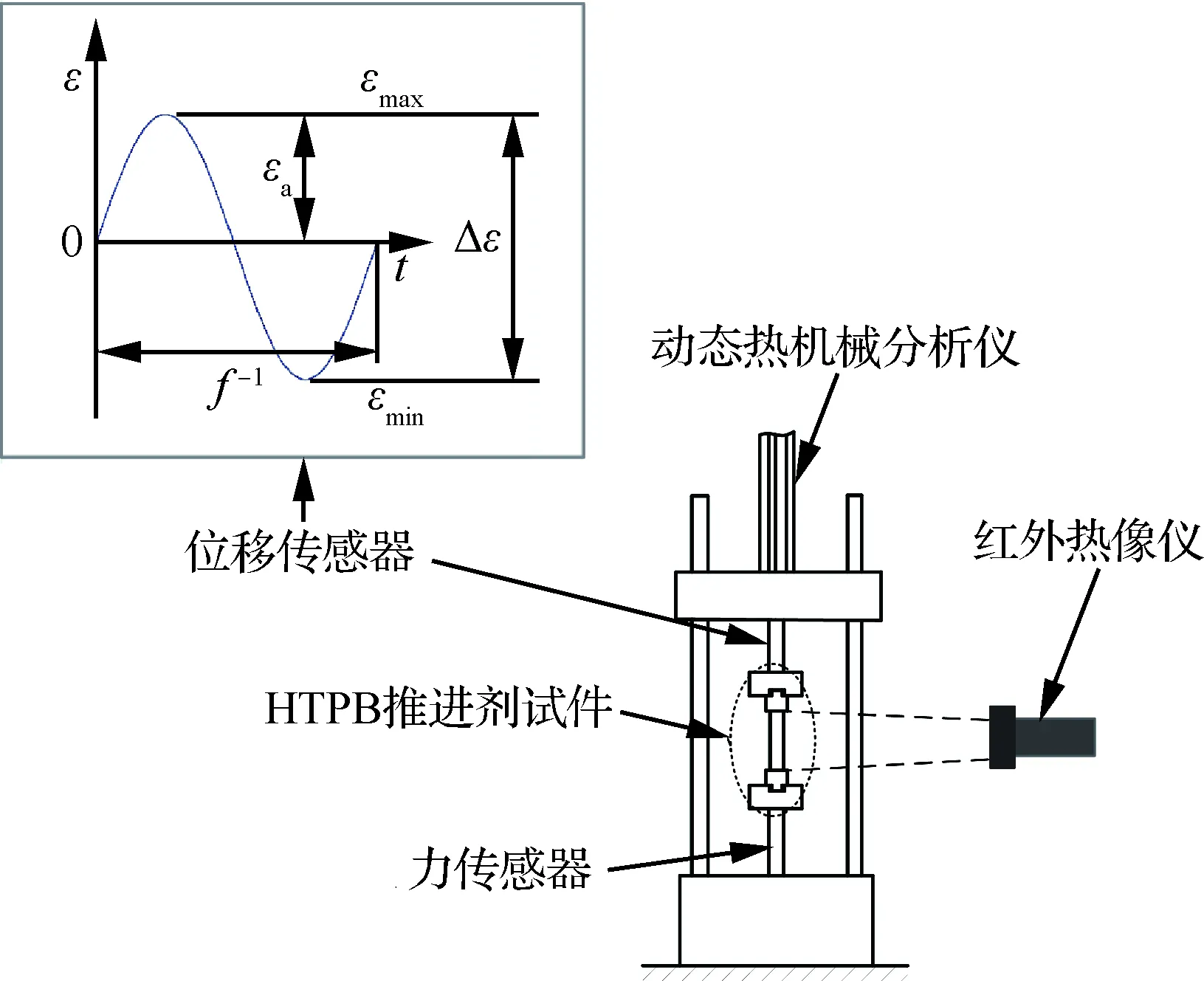
图2 DMA与红外热像仪示意图Fig.2 Schematic of DMA and infrared camera

2 循环应力软化

图3是HTPB推进剂在应变控制下的循环应力-应变关系(图中N为疲劳次数)，可知循环应力-应变形成了滞回圈。在复合推进剂疲劳过程中，材料经历了一个初始的“适应”阶段后，应力幅达到一定稳定饱和值，在这种饱和状态下出现稳定的滞后曲线。在疲劳“适应”过程中，材料内部微观结构不断发生变化，直到代表饱和状态的稳定状态出现为止。此后在材料的其余疲劳寿命周期，每周的滞回曲线基本保持不变。

值得注意的是，与金属相比，聚合物在疲劳过程中只会发生循环软化[17]，聚合物的成分、分子结构、温度和应变速率在大范围内变化也只能改变它的循环软化程度。

文献[18]指出，可利用“动态模量”来表征复合推进剂疲劳过程中应力软化的程度。图4给出了50 Hz、3种应变幅值下的动态模量，在疲劳次数达到10 000时，材料开始进入稳态状态，动态模量变化幅度逐渐减小，对应着疲劳初始阶段的应力降；动态模量最终趋于稳定值，意味着材料进入损伤稳定发展的状态，机械能与热能、储能间的转化达到了平衡。

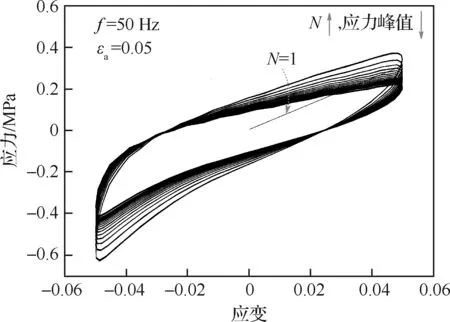
图3 不同疲劳次数时的滞回圈Fig.3 Hysteresis loops at different fatigue cycles

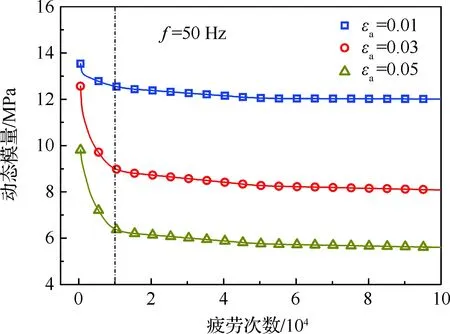
图4 动态模量随疲劳次数的变化Fig.4 Variation of dynamic moduli with fatigue cycles

3 疲劳中的能量耗散与产热

复合推进剂的疲劳是循环拉伸-回缩的过程。从分子机理看，受拉伸阶段外力对推进剂体系做的功，一方面改变分子链段的构象，另一方面克服分子链段间的摩擦力；在回缩阶段体系对外做功，一方面使构象改变重新卷曲，另一方面仍需克服链段间的摩擦力[19]。这样在拉伸-回缩的循环中，分子链的构象完全恢复，不损耗功，所损耗的功全用于克服内摩擦力，转化为热。内摩擦力越大，滞后现象越严重，消耗的功(内耗)也越大。

3.1 滞弹性耗散

对于存在黏性的滞弹性[20]材料来说，若加载应变为ε(t)=ε0sinωt，其中ε0为应变幅值，ω为角频率，则应力响应为

σ=σ0sin(ωt+δ)

(1)

式中：σ0为应力幅值；δ为滞后角(损耗角)，δ的正切值tanδ称为损耗因子(或阻尼损耗系数)，用来表征材料的阻尼特性。ε(t)还可以写为复数形式:ε*=ε0eiω t，则相应的应力响应为

σ*=σ0ei(ω t+δ)

(2)

复模量E*E*=E1+iE2为

(3)

E*的实数部分，即存储模量E1表征材料存储弹性变形能量的能力，其表达式为

E1=(σ0/ε0)cosδ

(4)

E*的虚数部分为损耗模量E2，体现材料黏性大小，表征材料耗散变形能量的能力，其表达式为

E2=(σ0/ε0)sinδ

(5)

复合推进剂属于黏弹性材料，由于滞后阻尼效应，其应变落后于应力，表现出强烈的滞弹性，导致疲劳中的应力-应变关系形成滞回线。每一滞回圈耗散的机械能D0(即滞回曲线围成的面积)为

(6)

式中：E*为动态模量。

表2给出了损耗角随应变幅值和频率的变化，其中损耗角均为滞回圈稳定时的测量值，当动态模量维持稳定时，损耗角也维持不变。从表中还可以发现，损耗角不随应变幅值增加而变化，意味着推进剂的阻尼损耗仅对频率敏感，随着频率的增大而增大。

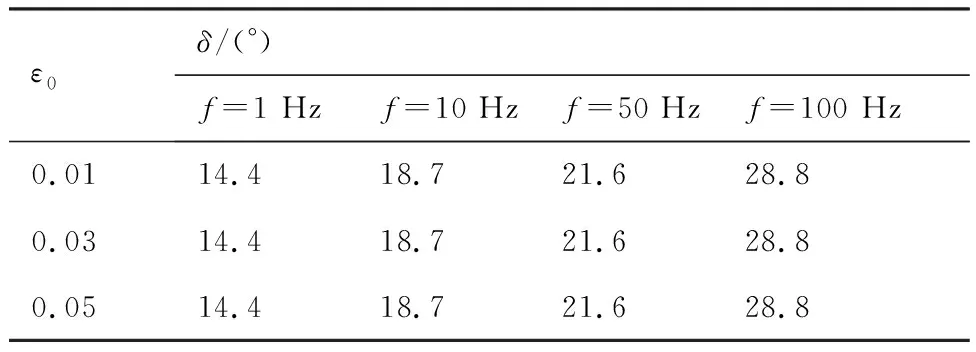
表2 损耗角随应变幅值和频率的变化

3.2 能量耗散密度与稳态温升

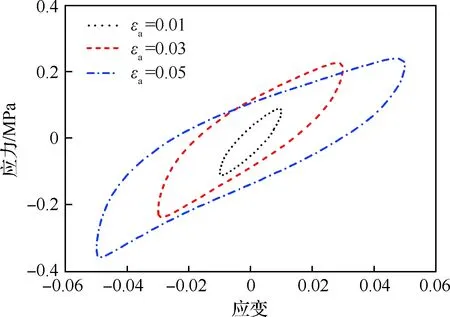
图5 不同应变幅值下的滞回圈(f=10 Hz)Fig.5 Hysteresis loops at different strain amplitudes (f=10 Hz)

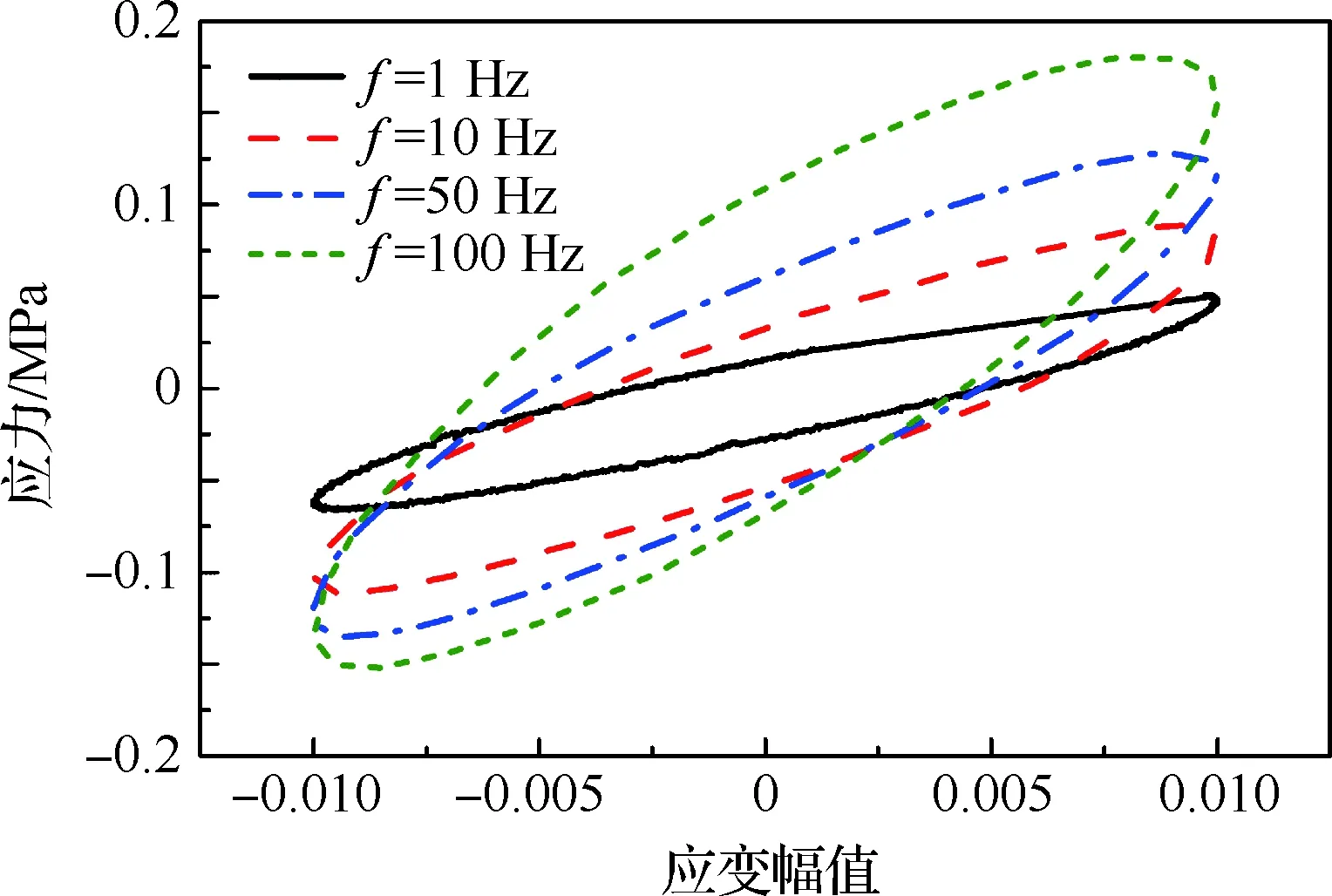
图6 不同频率下的滞回圈(εa=0.01)Fig.6 Hysteresis loops at different frequencies (εa=0.01)

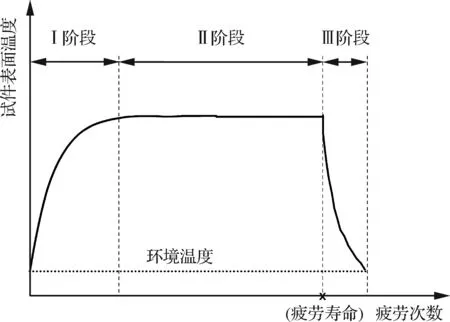
图7 典型温度变化曲线Fig.7 Typical curve of temperature variation

图7给出了HTPB推进剂试件在疲劳加载过程中的典型温度变化曲线，根据其变化趋势可以分为3个阶段。Ⅰ阶段为初始温升阶段：疲劳实验开始，随着循环次数的增加，推进剂释放大量的热量，实验开始时试件和环境的温差较小，对流过程中热量损失也比较少，试件表面产热速率大于试件和环境的热交换率。因此，试件表面温度快速升高。Ⅱ阶段为持续时间最长的温度稳定阶段：随着疲劳次数的增加，试件表面温度与环境温度通过与空气对流、辐射而平衡下来，当循环载荷下试件释放的热量等于散失的热量时，试件表面产热速率与试件和环境的热量交换速率达到平衡，温度变化达到相对稳定的状态，仅在小范围内波动。Ⅲ阶段为温度逐渐降低阶段：当试件开始出现裂纹时，达到使用寿命的终点，试件内部不再存在稳定的内热源，由于试件与环境的对流换热及与夹具间的热传导，试件表面温度逐渐下降，最终冷却至环境温度。

根据热力学第一定律，并假定推进剂疲劳过程中内部不存储能量[21](机械能100%转化为热能)，则有：

(7)

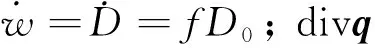
(8)

式中：ΔTS为稳态温升；NS为温度达到稳态时的疲劳次数。式(8)为与外界绝热条件下推进剂能量耗散与稳态温升的关系。由于D0反映了滞回圈的面积，所以温升与频率、应变幅值呈正相关关系。

3.3 温升的影响因素

材料在循环载荷下自身温度的升高与内热源的分布与强度、材料的热物性参数(导热系数、比热容等)以及热交换环境(对流、辐射)等相关，其中起决定作用的是变形引起的内热源产热量，影响最大的因素是载荷频率与应变幅值[22]。图8给出了不同频率和应变幅值下Ⅱ阶段的稳态温升值，可知增大加载频率和应变幅值的同时，试件的稳态温升也随之增加。拟合可得稳态温升值ΔTS与应变幅值εa和频率f之间的关系为

ΔTS=-0.913+12.166εaf

(9)

即ΔTS∝εaf，相关系数R2=0.99。在图9中，将预测结果与文献[4]在f=100 Hz、εa∈[0.01, 0.05]下的实验值进行对比，验证了式(9)的正确性。

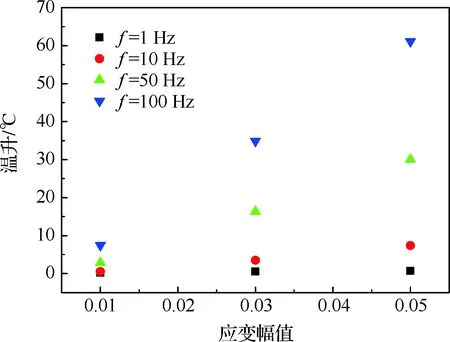
图8 不同频率下的稳态温升Fig.8 Stable temperature rise at different frequencies

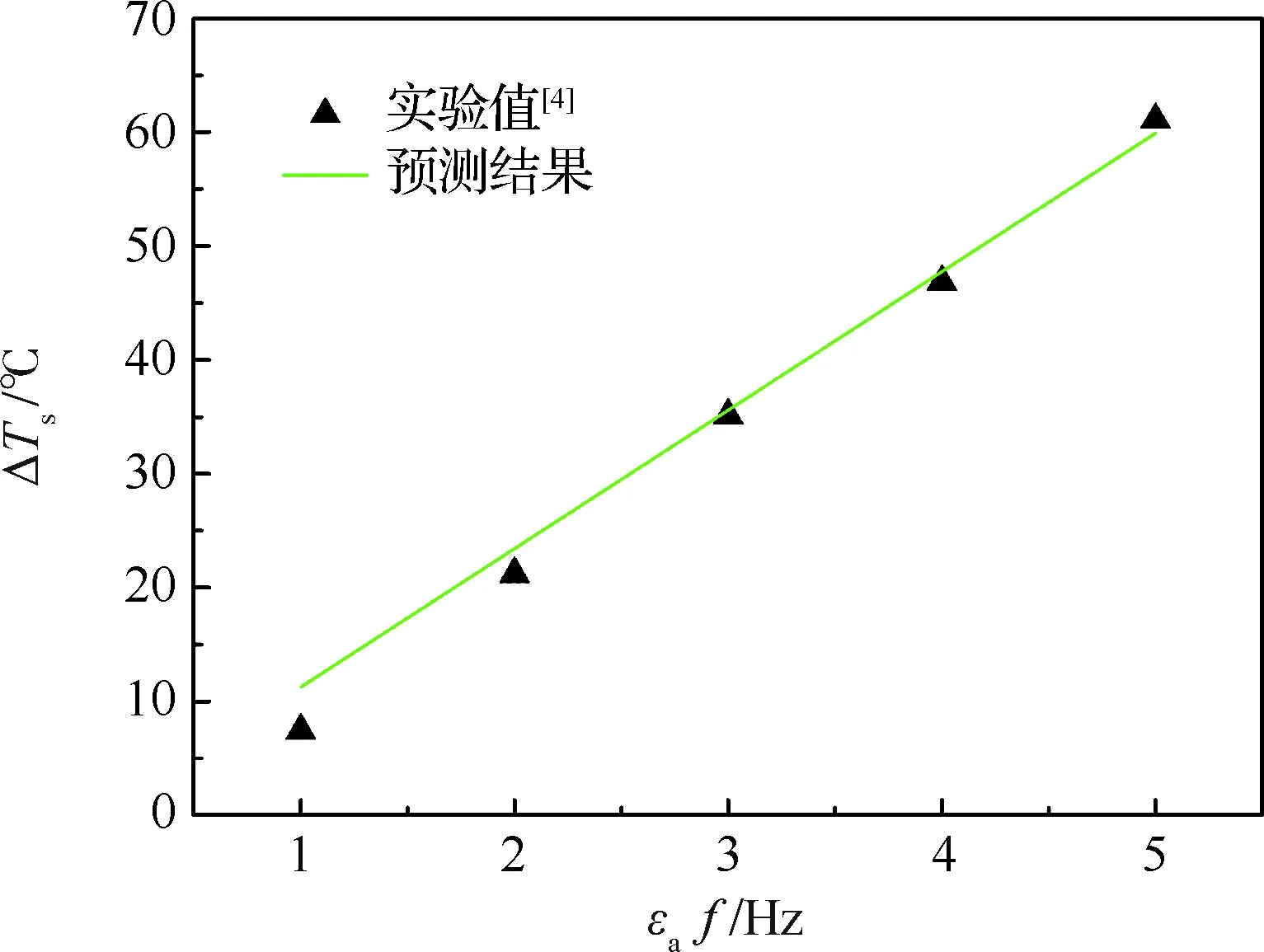
图9 预测温升与实验值的对比Fig.9 Comparison of predicted and experimental temperature rise

4 滞后温升的计算

4.1 温度场函数

图10为长方体试件的示意图，两端面边长均为2a，试件高度为b。试件上下两端面与刚性平板连接，假设连接面无摩擦，且刚性平板绝热。由于黏弹性滞后效应引起了材料产热，相当于在材料内部形成了内热源，将HTPB推进剂视为各向同性材料，则上述两端绝热的矩形体的温度场控制方程为

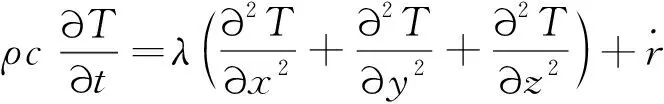
(10)

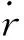
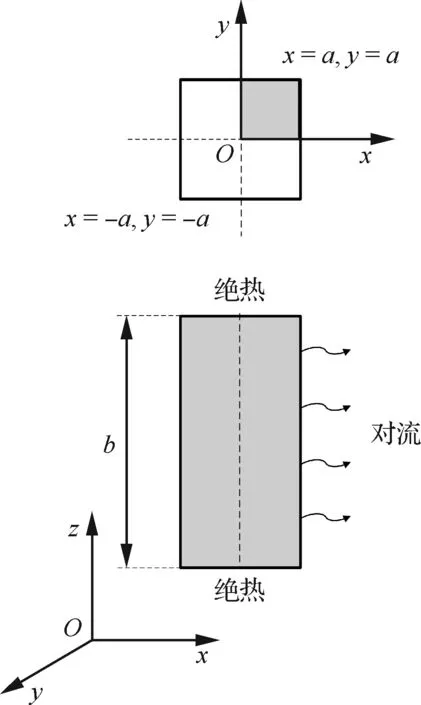
图10 计算模型示意图Fig.10 Schematic of calculated model

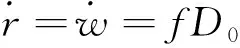
(11)

考虑第3类边界条件和试件的对称性，得到三维、非稳态、常物性、有内热源的导热微分方程:

(12)

式中：h为复合推进剂与空气的对流换热系数；T∞为环境温度; 0≤x≤a, 0≤y≤a, 0≤z≤b。

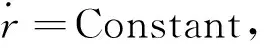
4.2 计算结果分析

数值仿真软件COMSOL Multiphysics通过求解偏微分方程组(多物理场)来实现真实物理现象的仿真[23]，在多物理场耦合计算方面具有很大的优势和可靠性。由于直接求解式(12)较为困难，因此利用COMSOL Multiphysics进行了仿真计算。

根据实验建立一个三维长方体模型，试件的材料属性见表1，边界条件如图10所示，计算区域为界面为5 mm×5 mm、高度为15 mm的长方体，上下边界绝热，4个侧面与外部空气为自然对流，环境温度为23 ℃。网格设置为物理场控制网格，单元尺寸为常规尺寸。

图11为t=83 s试件的温度云图，其中内热源强度为1×106W/m3(对应的加载参数为f=100 Hz，εa=0.05)。从图中可发现，长方体的中心区域与外围存在显著的温度梯度，而高度方向(z轴)的温度梯度很小。由于空气的持续冷却作用，外侧面温度偏低。

图12(a)为图11中z=7.5 mm截面的放大图，可进一步观察到，随着区域的增大，内部热流逐渐向外部作用，等温线的形状接近试件的上侧面轮廓。同样地，在图12(b)可明确x或y方向上热源由内向外扩散。

为了与实验环节所得的试件表面温升进行比较，提取了仿真结果中的温度数据(仿真时设定内热源的大小与实验中的稳态内热源强度一致，对应加载的不同应变幅值和频率)，对比结果如图13所示，图中实线为仿真结果，空心符号为实验结果。实验值与仿真结果误差较小，可预测不同加载条件下的试件表面温度演化情况。同样，仿真结果也揭示出内热源恒定的假设对计算结果的影响较小，因此假设较为合理，可以极大地提高计算效率。

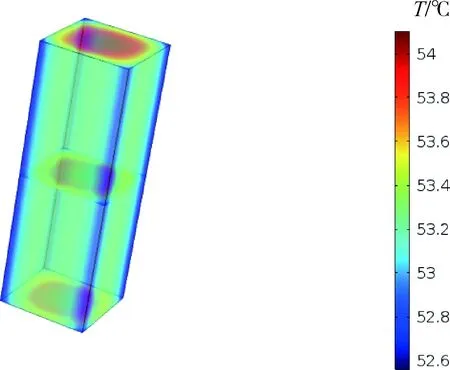
图11 t=83 s时试件的温度云图Fig.11 Temperature nephogram of specimen at t=83 s

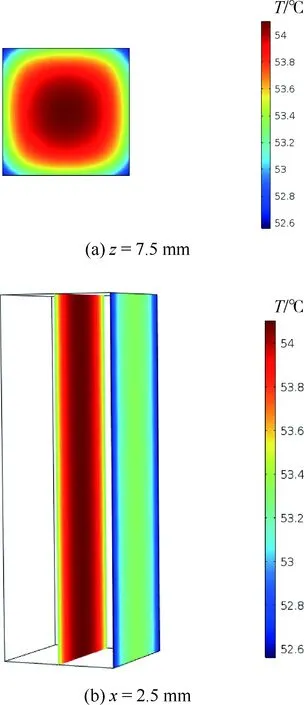
图12 不同截面处的温度云图Fig.12 Temperature nephogram of different cross- sections

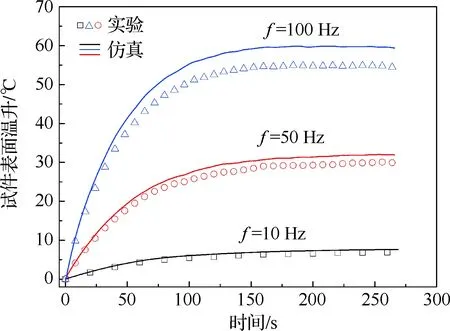
图13 试件表面温升仿真与实验结果对比(εa=0.5)Fig.13 Comparison of surface temperature rise of specimen between simulated and experimental results (εa=0.5)

5 结 论

针对复合推进剂在循环载荷下的能量耗散及其滞后温升问题，进行了实验和理论分析，得到以下结论：

1) 应变控制模式下，复合推进剂疲劳中的能量耗散主要受加载频率和应变幅值影响，能量耗散导致的试件表面温升最高可达61 ℃(加载条件为εa=0.05,f=100 Hz)。

2) 复合推进剂受循环载荷时，推进剂表面稳态温升值ΔTS与加载的应变幅值εa、频率f的乘积εaf呈正比关系，即：ΔTS∝εaf。

3) 通过对三维模型的有限元仿真，假定内热源恒定，得到了滞后温升的计算结果，与实验值较为吻合，可预测不同加载条件下的温升值。