低压电力通信系统中的人工蛛网及可靠性和性能计算与分析

张培培，邵方明，张震霄

（华东理工大学 数学系，上海 200237）

0 引 言

网络是关联系统的一种特殊情形，网络可靠性是度量网络性能好坏的指标。在以前的研究中，研究者通常用概率图建立具有不可靠点或边的网络模型。因此，网络可靠性指在给定的每条边或每个点的可靠性条件下，所有的终端节点可以相互连通的概率[1]，通常记为R(G)。本文的可靠性模型建立在边不可靠，点可靠的条件下。

智能电网是以物理电网为基础，将现代先进的传感测量技术、通信技术、信息技术、计算机技术和控制技术与物理电网高度集成而形成的新型电网。它以充分满足用户对电力的需求和优化资源配置、确保电力供应的安全性、可靠性和经济性、满足环保约束、保证电能质量、适应电力市场化发展等为目的，实现对用户可靠、经济、清洁、互动的电力供应和增值服务。随着智能电网在全球范围内的快速发展，中国国家电网公司决定以智能电网技术为基础，在全国范围内建设新型电网。低压电力线通信技术（LVPLC）作为终端用户与电力公司交换信息的直接手段，是智能电网的通信网络建设中可供选择的极具竞争力的技术手段。

由于低压配电网物理拓扑的未知性、复杂性与易变性，物理介质的共享性和多样性以及信道的强噪声干扰等特点，使得电力线通信可靠性较低，直接影响了其在智能电网建设中的大规模应用。近年来的研究主要有，提高PLC网络内点对点的通信成功率，包括：信道建模与快速估计[2]，传输特性与信号衰减特性研究[3]，跳频调制/解调技术研究等[4]；通过组网，建立网络中继，提高电力线通信网络的可靠性[5]。文献[6]针对电力线载波通信网络可靠性低的问题，研究了人工蛛网路由在低压电力线通信领域应用的可靠性。采用基于马尔科夫概率论模型改进的因子分解方法，对应用于低压电力线通信的人工蛛网结构的全端可靠性和抗毁度进行分析与计算，与传统的树形、星形、环状网络进行对比，证明了单层人工蛛网的高全终端可靠性。

然而，在实际中，往往不仅需要点对之间有连通的路，也需要这条路的长度有所限制[7]。例如，网络中每个点在传输数据时需要传输时间t，若总传输时间限制在T内，那么参与传输的点数不能超过T t，这就意味着传输的路径长度受到限制。在无线传感器网络中，传输数据时则有跳数限制。因此，在研究人工蛛网可靠性问题时加入直径限制是十分必要的。文献[8]中介绍了直径限制，指的是网络中所有路的长度均不能超过一个给定的正整数D。直径限制下的网络可靠性（DCNR）指所有的终端节点可以通过一条长度不大于D的路径相互连通的概率[9]，记为R(G,D)。

事实上，对有些网络仅仅需要了解部分端点间通信能力的大小，但不必知道具体是哪些点。例如，移动通信需要实现至少90%用户的接入能力，却不需要知道这些用户是谁；又如野战通信网的故障判断为网络内15%的端点传输中断[10]，该判据也仅需要知道传输中断节点的数量。文献[11]在此基础上提出了连通比的概念及基于连通比的有源网络可靠性模型，并进一步研究了它的上界问题。连通比是能够相互通信的端点数k与总端点数n的比值。它体现了网络对保障有效服务的用户接入比例的最低要求。本文在以上的基础上考虑直径限制下保证一定连通比的低压电力线通信人工蛛网可靠性问题。不同于传统的可靠性模型，本文中的网络要实现直径限定下至少一定比例的节点能够相互通信而不是指定的K个节点。

网络可靠性算法包括精确算法和近似算法。文献[12]介绍了利用生成树计算网络可靠性的精确算法。R(G)可以通过评估表示生成树的操作状态事件的并集的概率来获得。将这些相互独立的事件分别记为E1,E2,…,En，那么至少一个时间发生的概率用文献[13]中的不交和定理计算即为：

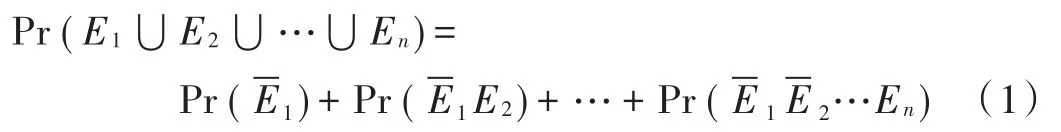
综上，本文主要研究低压电力下单层人工蛛网在直径限制及连通比限制下的可靠性分析与计算问题。通过找到实现直径限制下至少一定比例的节点能够相互通信的子图及生成树来计算其可靠性。仿真结果表明人工蛛网拓扑结构在连通比及直径限制下具有较高的通信可靠性。

1 可靠性数学模型与人工蛛网

用无向图G(V,E)表示人工蛛网网络拓扑，其中V={v1,v2,…,vn}是网络中的节点集，E={e1,e2,…,em}是边集，n为点的个数，m为边的个数。假设点是始终运行的，边有失效和运行两种状态，各边连通的概率相互独立，边e运行的概率为p，失效的概率为q=1-p。

为行文方便，引用文献[11]中的定义：

定义1：设k为在网络节点集V中能够相互通信的端点数，把k与n的比值κ=k n称为连通比，κ∈[0,1]。

显然，在网络G中，要保证连通比κ，则能够成功通信的端点数至少为（表示对*上取整）。

定义2：在网络G(V,E)中，在D限制下且在端点集V中至少k个端点间能够相互通信的概率称为直径限制下保证连通比的网络可靠性，记为Rk(G,D)。

由定义2可知，只要G的任何一个端点数大于或等于k的子图连通就能保证G的连通比不低于给定的κ。那么，只要计算G的端点数大于或等于k的所有子图在D限制下的可靠性，即可得Rk(G,D)。易知，这些子图的个数为：

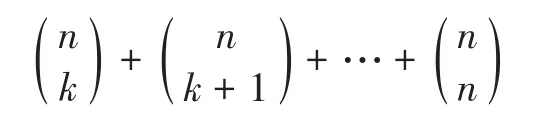
2 可靠性Rk(G,D)的计算

为了更清楚地说明直径限制下保证连通比的网络可靠性的定义，在例1中选定节点数为4的单层人工蛛网解释说明上述Rk(G,D)的计算。

例1：如图1所示，给定直径限制D=2，连通比κ=0.6，每条边通信的概率均为p=0.9，不通信的概率为q=0.1。

由于给定的连通比κ=0.6，因此只要保证至少个点连通。问题转化为求个子图在直径限制下的全终端可靠性问题。本文将采用先找出子图的所有生成树，再根据D=2，找出所有冗余树，最后用式（1）计算R0.6(G,2)。

图1是单层蛛网包含3个点和4个点的子图及它们的所有生成树。由于生成树T17～T28的直径均为3大于D，因此T17～T28是冗余树，在计算时可以删去。结合式（1），有：

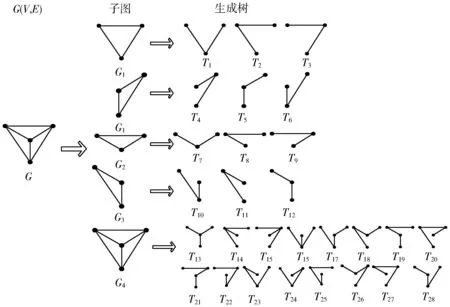
图1 点数为4的单层人工蛛网Fig.1 Single-layer artificial cobweb network with 4 nodes

3 单层蛛网高可靠性的仿真例子

低压配电网是一种树形网络，因此分析这种网络的直径限制下基于连通比的可靠性具有实际的意义。本文采用能代表各自网络特性的树形网络、星形网络、单层环网及单层蛛网进行分析与比较。为保证直径限制下基于连通比的可靠性的公平性，选定节点数均为6的上述网络，直径限定D=3，连通比κ=0.8，每条边通信的概率均为p。

由于给定的连通比κ=0.8，因此只要保证至少k=个点连通。问题转化为求个子图在直径限制下的全终端可靠性问题。先找出子图的所有生成树，再根据D=3，找出所有冗余树，最后用式（1）计算R0.8(G,3)。

图2a）是树形网络包含5个点和6个点的子图。其中Ga2，Ga3，Ga4是不连通子图，所以没有生成树。又因为D=3，因 此Ta2～Ta4是 冗 余 树 ，在 计 算 时 可 以 删去R0.8(Ga,3)=Pr(E1)=p4。

图2b）是星形网络包含5个点和6个点的子图，其中Gb2是不连通子图。由星形图的对称性知，子图Gb1有5个。因此，Ga保证至少5个点连通的生成树有Tb2和5个Tb1。D=3，Tb2和Tb1不是冗余树。所以，R0.8(Gb,3)=Pr(E1∪E2)=p4+4p4q。

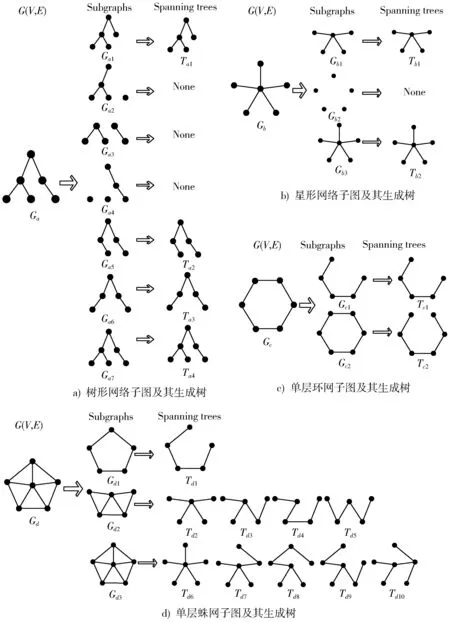
图2 树形、星形、单层环网及单层蛛网拓扑图Fig.2 Topology diagrams of the tree，star，single-layer ring and single-layer cobweb networks

图2c）是单层环网包含5个点和6个点的子图。由环网的对称性知，Gb保证至少5个点连通的子图Gc1有5个，生成树Tc2有6个。在直径限制下，其所有生成树均为冗余树，因此，R0.8(Gc,3)=0。

图2d）是单层蛛网包含5个点和6个点的子图。由蛛网的对称性，生成树Td1～Td10的个数分别为5个、1个、20个、4个、12个、1个、10个、10个、15个、5个。考虑直径限制，有：

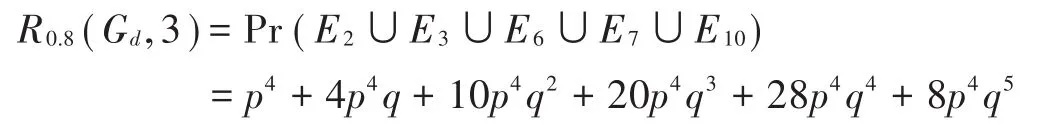
同理，当D=2，κ=0.8时，R0.8(Ga,2)=0，R0.8(Gb,2)=p4+4p4q，R0.8(Gc,2)=0，R0.8(Gd,2)=p4+4p4q；当D=4，κ=0.8时，R0.8(Ga,4)=p4+2p4q，R0.8(Gb,4)=p4+4p4q，R0.8(Gc,4)=p4+4p4q+3p4q2，R0.8(Gd,4)=p4+4p4q+10p4q2+0p4q3+34p4q4+12p4q5。

图3a）～图3c）分别是树形网络、星形网络、单层环网与单层蛛网在κ=0.8时，D=2，D=3和D=4限制下的可靠性计算结果对比图。从图3a）可以看出，在相同的连通比限制下，当直径限制为2时，单层蛛网在连通比及直径限制下的可靠性与星形网络相同，远高于树形网络及单层环网；而当直径限制为3或4时，单层蛛网在连通比及直径限制下的可靠性均远高于其他网络。当κ=0.8，D=1时，由于Ga，Gb，Gc，Gd在连通比限制下的子图生成树的直径均大于1，所以R0.8(Ga,1)=R0.8(Gb,1)=R0.8(Gc,1)=R0.8(Gd,1)=0；当κ=0.8，D≥ 5时，由于Ga，Gb，Gd在连通比限制下的子图生成树的直径均小于等于4，所以R0.8(Ga,D)=R0.8(Ga,4)，R0.8(Gb,D)=R0.8(Gb,4)，R0.8(Gd,D)=R0.8(Gd,4)，而 经 计 算 得R0.8(Gc,D)=R0.8(Gc,4)，与图3b）情况相同。因此，在相同的连通比限制下，人工蛛网拓扑结构在连通比及直径限制下具有较高的通信可靠性。

为了验证在相同直径限制下，人工蛛网拓扑结构在连通比及直径限制下也具有较高的通信可靠性，在给定D=3，分析k取不同数值时Ga，Gb，Gc，Gd的可靠性。计算结果见表1。

显然，在取相同的p(p≠0)值时，单层人工蛛网的Rκ(Gd,3)恒大于其他三个网络。综上，在低压电力通信系统中，与传统的树形网络、星形网络及单层环网相比，无论D，κ值如何变化，单层人工蛛网拓扑结构在连通比及直径限制下都具有较高的通信可靠性。

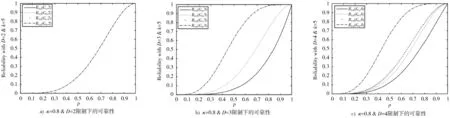
图3 κ=0.8限制下的可靠性Fig.3 Reliability asκ=0.8

表1 D=3，k取不同数值限制下的可靠性对比Table 1 Comparison of reliability atD=3and different values ofk

4 结 论

本文考虑直径限制下保证一定连通比的低压电力下人工蛛网可靠性问题。对树形网络、星形网络、单层环网及单层蛛网在连通比及直径限制下的可靠性进行分析与比较，得出人工蛛网拓扑结构在连通比及直径限制下具有较高的通信可靠性。仿真实例说明人工蛛网的通信可靠性比较好。

注：本文通讯作者为邵方明。